Problem - C - Codeforces

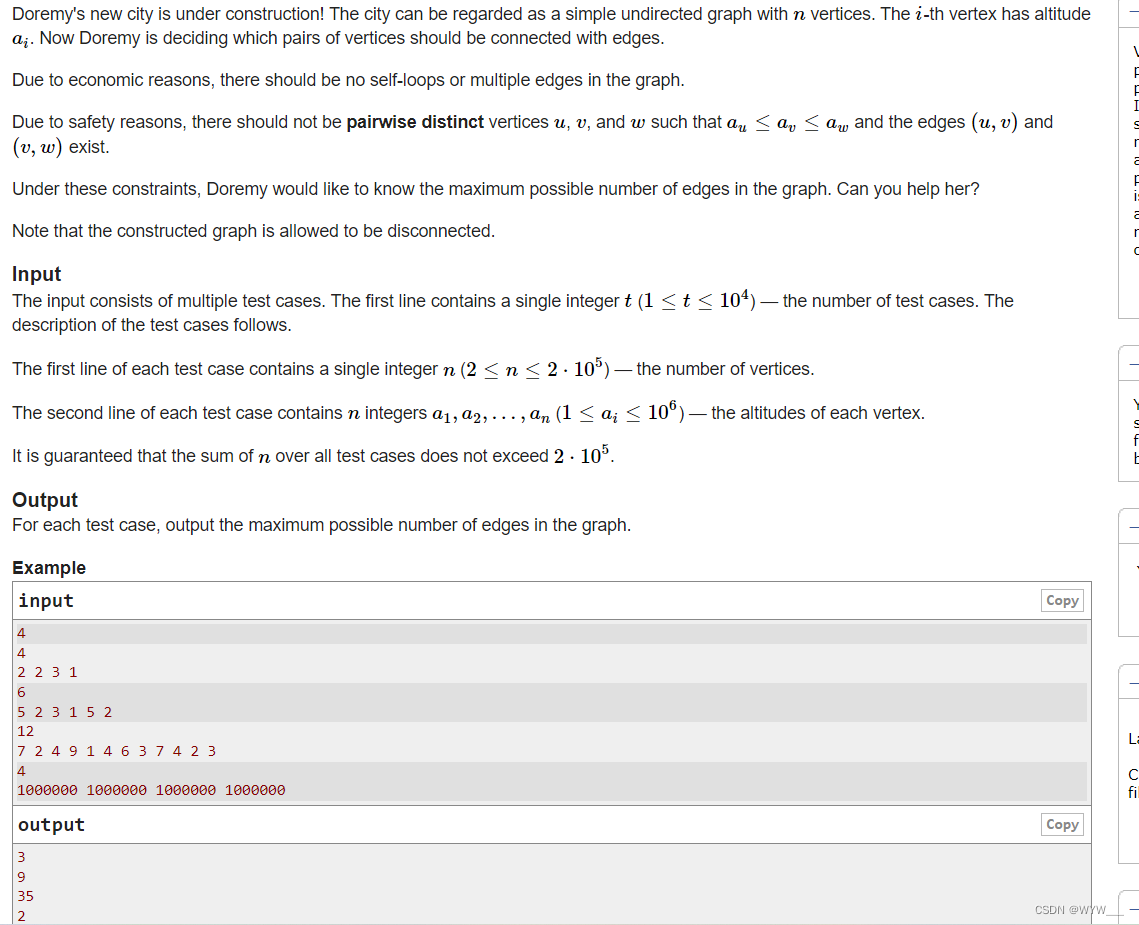
Doremy的新城市正在建设中! 这个城市可以被看作是一个有n个顶点的简单无向图。第i个顶点的高度为ai。现在，多雷米正在决定哪些顶点对应该用边连接。

由于经济原因，图中不应该有自循环或多条边。

由于安全原因，不应该有成对的不同顶点u、v和w，使au≤av≤aw和边（u,v）和（v,w）存在。

在这些约束条件下，Doremy想知道图中最大可能的边数。你能帮助她吗？

请注意，所构建的图允许是不连接的。

输入
输入由多个测试案例组成。第一行包含一个整数t（1≤t≤104）--测试案例的数量。测试用例的描述如下。

每个测试用例的第一行包含一个整数n（2≤n≤2⋅105）--顶点的数量。

每个测试案例的第二行包含n个整数a1,a2,...,an（1≤ai≤106）--每个顶点的高度。

保证所有测试案例的n之和不超过2⋅105。

输出
对于每个测试案例，输出图中最大可能的边数。

例子
inputCopy
4
4
2 2 3 1
6
5 2 3 1 5 2
12
7 2 4 9 1 4 6 3 7 4 2 3
4
1000000 1000000 1000000 1000000
输出拷贝
3
9
35
2

 题解:
题中说不允许出现三条边相连类似,wi <= wj <= wk的形式

那我们就构造不是这样的形式即可

记录每个f[x]的值

遍历f[x],找到小于x的值有l多少,与大于x的值r有多少

理论上每个大于x的值,两边是随便放x的值,与小于x的值的,一个大于x的值,可以构建l + f[x]条边,

那么r个大于的值,就可以构建(l + f[x])*r条边

还有一种情况,所有点值相等,n/2

#include<iostream>
#include<algorithm>
#include<cstring>
#include<string>
#include<map>
#include<vector>
#include<queue>
using namespace std;
#define int long long
//1 1 3 3 3
void solve()
{
	map<int,int> f;
	int n;
	cin >> n;
	for(int i = 1;i <= n;i++)
	{
		int x;
		cin >> x;
		f[x] ++;
	}
	int s = 0;
	int ans = 0;
	for(auto [k,v]:f)
	{
		s += v;
		ans = max(s*(n-s),ans);
	}
	if(ans == 0)
	{
		ans = n/2;
	}
	cout<<ans<<"\n";
}
signed main()
{
//	ios::sync_with_stdio(false);
//	cin.tie(0);
//	cout.tie(0);
	int t = 1;
	cin >> t;
	while(t--)
	{
		solve();
	}
}
//5 7
//2
//3 1
//4