哈夫曼树

首先给我们一串权值，然后我们需要让这串权值组成一个树，然后当他的wpl最小

我们可以发现当他的小权值离根节点越远，大权值离根节点越近的时候，我们这个时候构建出来的树就是wpl最小的树，也就是我们说的哈夫曼树

构建的方法

我演示一个当我们有这样子的一串权值的时候

我们先选出3 5也就是他最小的和第二小的，把最小的当成左孩子，另一个为右孩子，然后他们的父节点就是3+5=8，就是8，然后再把8选入原串中，把我们刚刚选出来的两个数字去除，然后再来选两个最小的和第二小的数

最后我们就可以得到

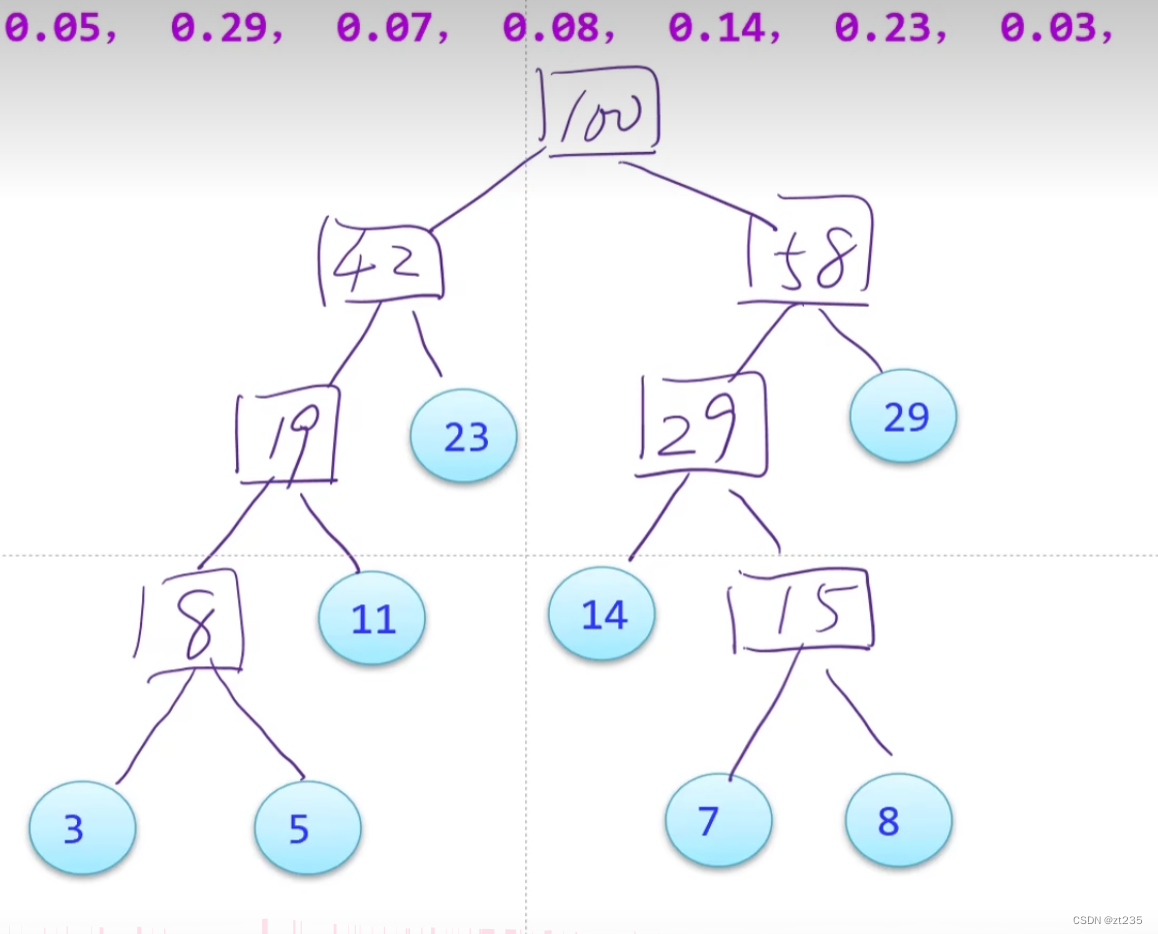
这样子的一个树，这就是我们的哈夫曼树

哈夫曼编码

左孩子的为0，右孩子为1

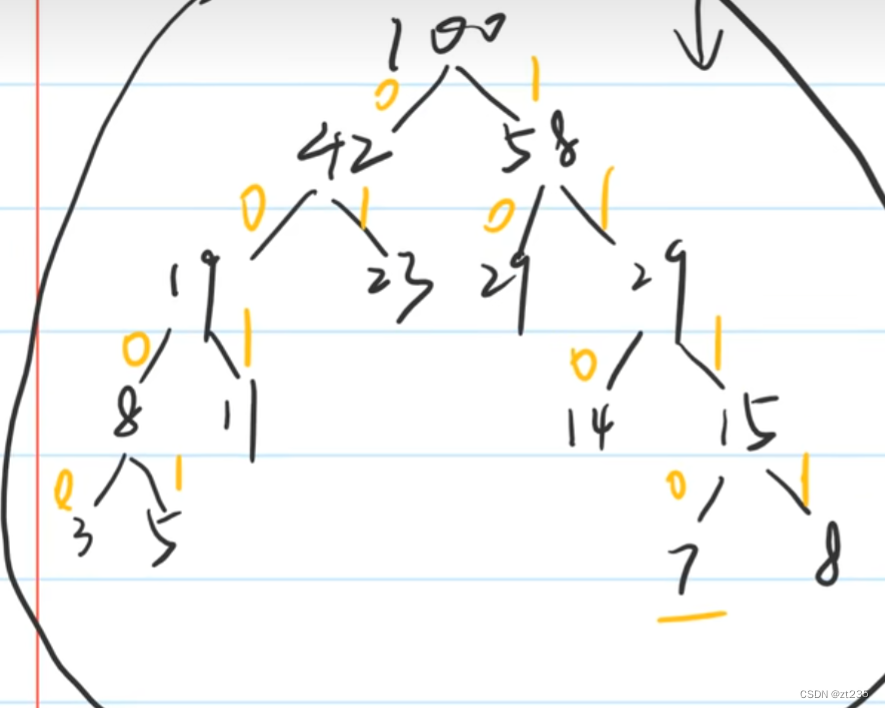
这东西讲起来很难麻烦，举个例子，7的哈夫曼编码就是1110，从树的根节点往下找就ok

再比如8的哈夫曼编码000，再比如11的哈夫曼编码001

这就是哈夫曼树和哈夫曼编码，他的构建代码我还没搞出来/(ㄒoㄒ)/~~

最小生成树

最小生成树就是，当我们在解决一些问题的时候，比如求好几个村子现在要建工路，如果建造可以让他的花费最小而且每个村子可以连接到一起，这就是最小生成树问题

Kruskal算法

就是我们一般情况下会得到一串这样子的东西

当然他不是排好的数字，而是要我们自己排序，我们把它排好之后，每次都取出最小的那个权值对应的连接的边，如果我们取出来的边导致原本的图成环了（并查集来判断），那我们就不要这个边，换下一条，直到我们取出来的边的数目为节点数减1，算法结束

建议看一下，只看文字不太好理解

【最小生成树(Kruskal(克鲁斯卡尔)和Prim(普里姆))算法动画演示】https://www.bilibili.com/video/BV1Eb41177d1?vd_source=c9016f395efdf6f1094ae706e81044e3

具体代码实现就是

#include <stdio.h>
int fa[100100];
int b[100100];
struct mei
{
	int x,y,z;
}a[100100];

int root(int x,int fa[])
{
	if(fa[x]!=x)
	{
		fa[x]=root(fa[x],fa);
	}
	return fa[x];
}

void he(int x,int y)
{
	fa[x]=y;
}

void kuai(int left,int right)
{
	int i,j,teap,t,t1,t2;
	if(left>right)
	{
		return;
	}
	teap=a[left].z;
	int teap1=a[left].x;
	int teap2=a[left].y;
	i=left;
	j=right;
	while(i!=j)
	{
		while(teap<=a[j].z&&i<j)
		{
			j--;
		}
		while(teap>=a[i].z&&i<j)
		{
			i++;
		}
		if(i<j)
		{
			t=a[i].z;
			a[i].z=a[j].z;
			a[j].z=t;
			t1=a[i].x;
			a[i].x=a[j].x;
			a[j].x=t1;
			t2=a[i].y;
			a[i].y=a[j].y;
			a[j].y=t2;
		}
	}
	a[left].z=a[i].z;
	a[left].x=a[i].x;
	a[left].y=a[i].y;
	a[i].z=teap;
	a[i].x=teap1;
	a[i].y=teap2;
	kuai(left,i-1);
	kuai(i+1,right);
	return;
}

int main()
{
	int n,m,k;
	long long sum=0,kk,i,teap,j,l,r;
	scanf("%d%d%d",&n,&m,&k);
	for(i=1;i<=m;i++)
	{
		scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].z);//x,y表示连接的地方z表示美丽度
	}
	kuai(1,m);
	//排序大的放前面
	/*for(i=1;i<=m;i++)
	{
		b[i]=a[i].z;
	}
	for(i=1,j=m;i<=m;i++,j--)
	{
		a[i].z=b[j];
		//printf("%d ",a[i].z);
	}*/
	for(i=1;i<=n;i++)
	{
		fa[i]=i;
	}
	//下面最小生成树
	for(i=m,kk=0;i>=1&&kk<k;i--)
	{
		l=root(a[i].x,fa); r=root(a[i].y,fa);
		//printf("%d %d\n",l,r);
		if(l!=r)//不在一起就合并
		{
			he(l,r);
			kk++;
			sum=sum+a[i].z;
		}
	}
	printf("%lld",sum);
	return 0;
}

我这个题目是求最大的，排序不同而已

Prim算法

这就是一个图，我们从1开始，然后我们找到与1相连的边上最短的线，把1纳入集合（就是已读取的顶点），然后我们就发现3最小，于是就连上7，然后把7纳入集合

然后我们找与1和7相连的线上最小的数，并把它纳入集合，同时不可以让他形成环，最后我们就得到了一个

这就是prim算法的思想

代码具体实现就是

#include <stdio.h>
int a1[5001],a2[5002],a[5001][5001];
int main()
{
	int n,m,i,j,k;
	int x,y,z,sum=0;
	scanf("%d%d",&n,&m);
	for(i=1;i<=n;i++)
	{
		for(j=1;j<=n;j++)
		{
			a[i][j]=9999999;//将每个点都是可读
		}
	}
	for(i=1;i<=m;i++)
	{
		scanf("%d%d%d",&x,&y,&z);
		if(z<a[x][y])//如果有更短的路径就替换
		{
			a[x][y]=z;
			a[y][x]=z;
		}
	}
	for(i=0;i<=n;i++)
	{
		a2[i]=99999999;//每个点都可以访问
	}
	a2[1]=0;
	for(i=1;i<=n;i++)
	{
		k=0;
		for(j=1;j<=n;j++)
		{
			if(!a1[j]&&a2[j]<a2[k]) k=j;
		}
		//printf("这里是k=%d",k);
		/*if(k==0)
		{
			printf("orz");
			return 0;
		}*/
		a1[k]=1;//表示被读取了
		for(j=1;j<=n;j++)
		{
			if(!a1[j]&&a[k][j]<a2[j])
			{
				a2[j]=a[k][j];
			}
		}
	}
	for(i=1;i<=n;i++)
	{
		sum=a2[i]+sum;
	}
	if(sum>9999999)
	{
		printf("orz");
		return 0;
	}
	printf("%d",sum);
}

我的建议是去看看这个视频

【最小生成树(Kruskal(克鲁斯卡尔)和Prim(普里姆))算法动画演示】https://www.bilibili.com/video/BV1Eb41177d1?vd_source=c9016f395efdf6f1094ae706e81044e3

这大佬讲的是真的好！！！