文章目录
- 一、背景
- 二、目标
- 三、计算
- 3.1 S曲线基本形式
- 3.2 S曲线变换
- 3.3 参数计算
- 3.4 S曲线中心对称条件
- 四、总结
- 五、附件
一、背景
S曲线因具备良好可控的平滑性、单调性、连续可导性等优点,常作为各类电机升降速曲线。当前多数S曲线的介绍文章未给出推导过程,以及部分文章采用了截取S曲线的近似处理方式,导致不能直观的理解该曲线的相关性质。本文主要介绍S曲线变换的推导过程,以加深对该曲线的理解。
二、目标
① 计算经过任意不同两点的S曲线方程
② 可调节曲线平滑度
③ 可调节曲线对称度
④ 绘制其图像
三、计算
3.1 S曲线基本形式
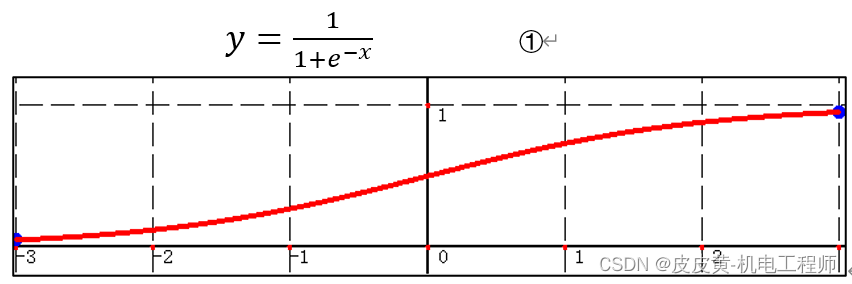
3.2 S曲线变换
将基本形式的S曲线进行X,Y方向平移及比例变换过程如下:
第一步:进行X轴比例变换,比例系数为N(N≠0)
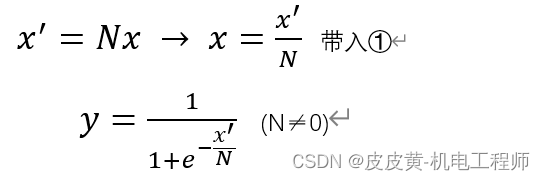
变换后S曲线方程为:
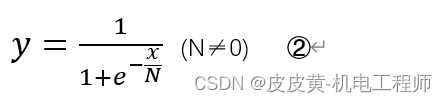
第二步:进行X轴平移变换,平移系数为A
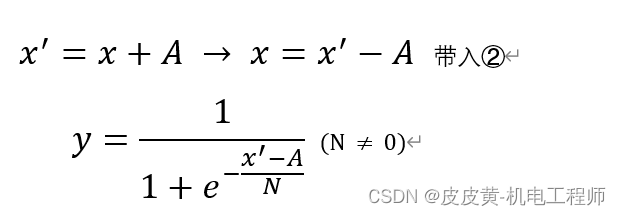
变换后S曲线方程为:
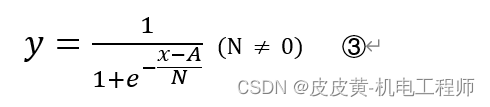
第三步:进行Y轴比例变换,比例系数为K(K≠0)
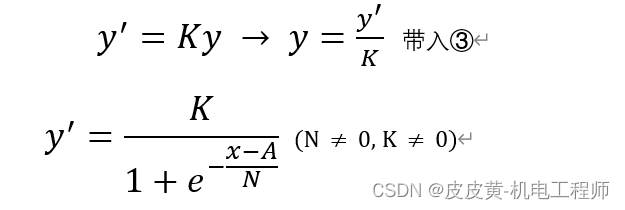
变换后S曲线方程为:
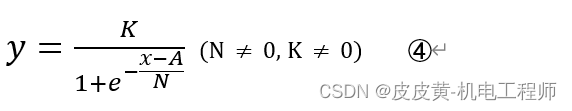
第四步:进行Y轴平移变换,平移系数为B
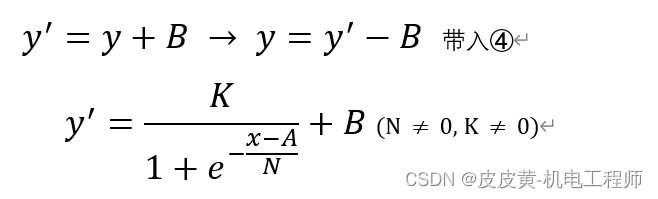
变换后S曲线方程为:
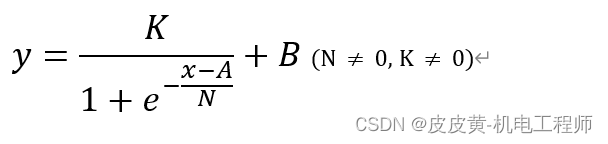
最终得到S曲线变换之后函数关系式:
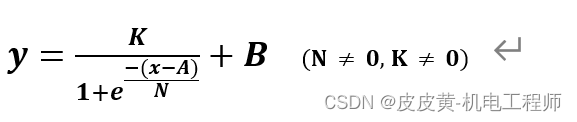
其中:
N-X轴方向比例变换系数
K-Y轴方向比例变换系数
A-X轴方向平移系数
B-Y轴方向平移系数
3.3 参数计算
要求变换之后的S曲线经过P1(X1,Y1),P2(X2,Y2)两点,可建立方程
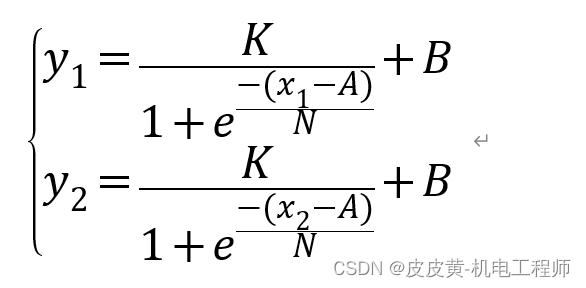
方程有N,K,A,B四个未知数,需要给定2个参数由用户设定,此处选择N,A,则可求得K,B值为:
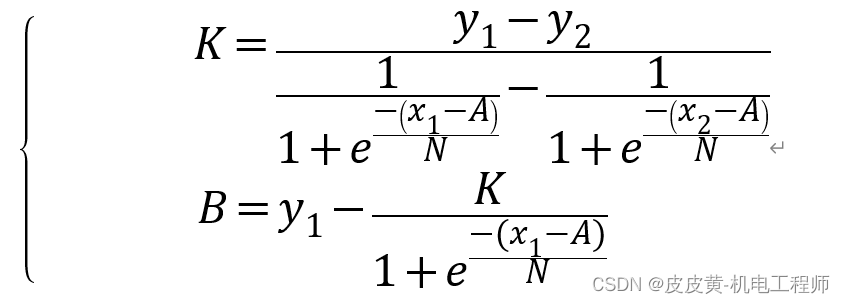
其中N值作为X轴方向比例变换系数,N>1时,S曲线X方向放大,N<1时,S曲线X方向缩小,可以将N值等效为S曲线的平滑度调节参数
其中A值X轴方向平移系数,A>0时,S曲线向X正方向平移,A<0时,S曲线向X负方向平移,可以将A值等效为S曲线的对称度调节参数
3.4 S曲线中心对称条件
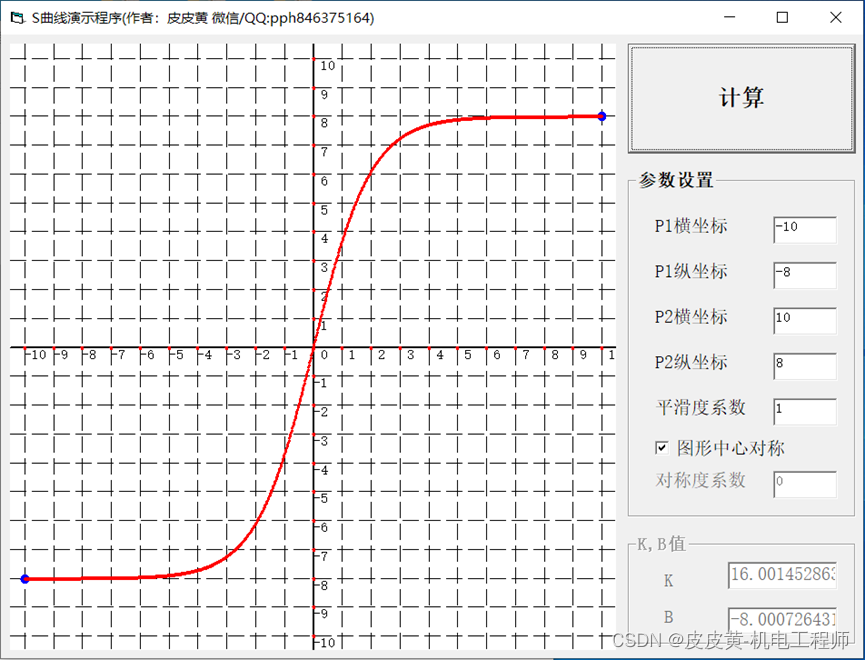
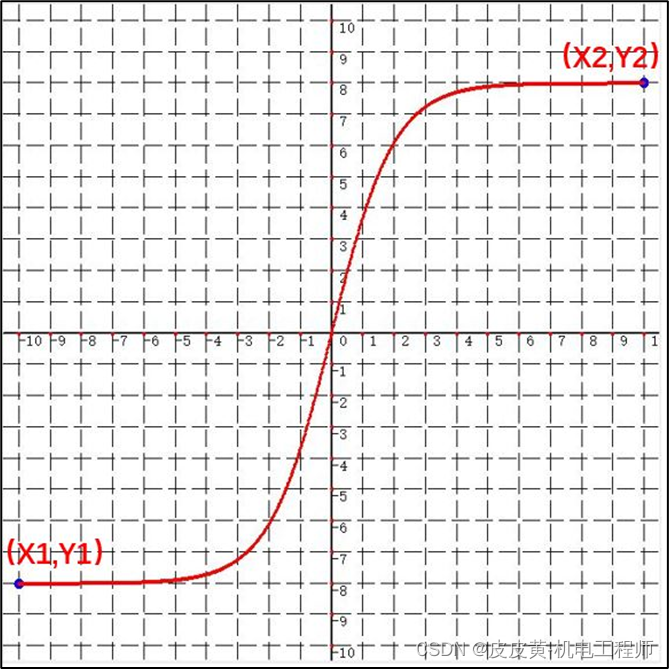
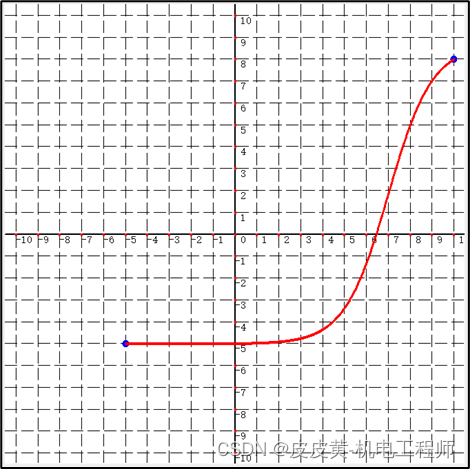
当随意给定N,A值时,S曲线容易出现失真,如下图所示
为确保经过P1,P2两点的S曲线也为中心对称,则要求S曲线经过P1P2连线的中点P0(X0,Y0),如图所示
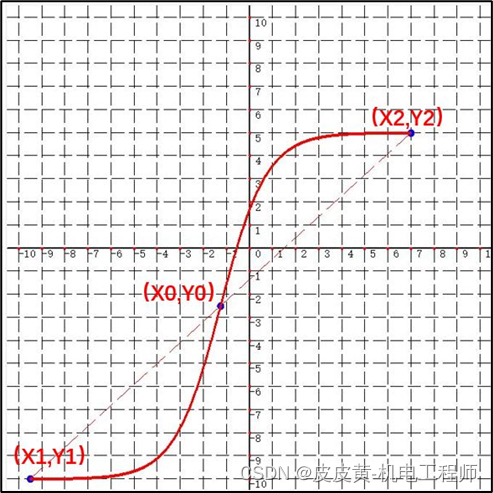
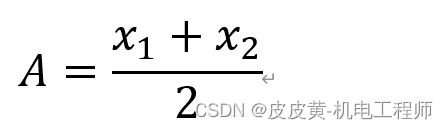
则可建立三个等式

N由用户设定,可求得A值
四、总结
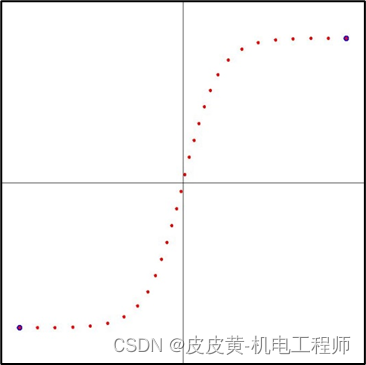
通过上述计算,完成了目标中的4点要求。在不同的应用场景中,可以根据实际情况去对该S曲线进行灵活处理。S曲线代表的v-t图像中对其进行求导可以求得a-t关系,S曲线代表的轨迹图像中进行微积分处理可得到沿线长方向上的等分点。
该曲线不足之处在于应用过程中的计算量较大,在需要实时处理的场景当中会对设备的计算能力要求较高,例如在电机动态S曲线升降速的单片机应用场景中会有较大难度
五、附件
提供一个S曲线的演示程序DEMO
链接: https://download.csdn.net/download/LuDanTongXue/87682727