目录
题目:剑指 Offer 54. 二叉搜索树的第k大节点 - 力扣(Leetcode)
题目的接口:
解题思路:
代码:
过啦!!!
题目:剑指 Offer 55 - I. 二叉树的深度 - 力扣(Leetcode)
题目的接口:
解题思路:
代码:
过啦!!!
题目:剑指 Offer 55 - II. 平衡二叉树 - 力扣(Leetcode)
题目的接口:
解题思路:
代码:
过啦!!!
写在最后:
题目:剑指 Offer 54. 二叉搜索树的第k大节点 - 力扣(Leetcode)

题目的接口:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int kthLargest(TreeNode* root, int k) {
}
};解题思路:
因为平衡二叉树的特点是,走中序遍历是一个升序数组,
题目要求找出第k大的值,
那不难想到,我们只需要倒着中序遍历平衡二叉树就行,
每次让k--,只要k==0就表明找到了:
代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int kthLargest(TreeNode* root, int k) {
//走中序遍历
dfs(root, k);
return ans;
}
private:
//记录k节点的值
int ans = 0;
//走一个倒序的中序遍历,让k值每走一个节点就--
void dfs(TreeNode* root, int& k) {
if(root == nullptr) return;
dfs(root->right, k);
//找到题目要求节点,记录ans值
if(--k == 0) {
ans = root->val;
return;
}
dfs(root->left, k);
}
};过啦!!!

题目:剑指 Offer 55 - I. 二叉树的深度 - 力扣(Leetcode)
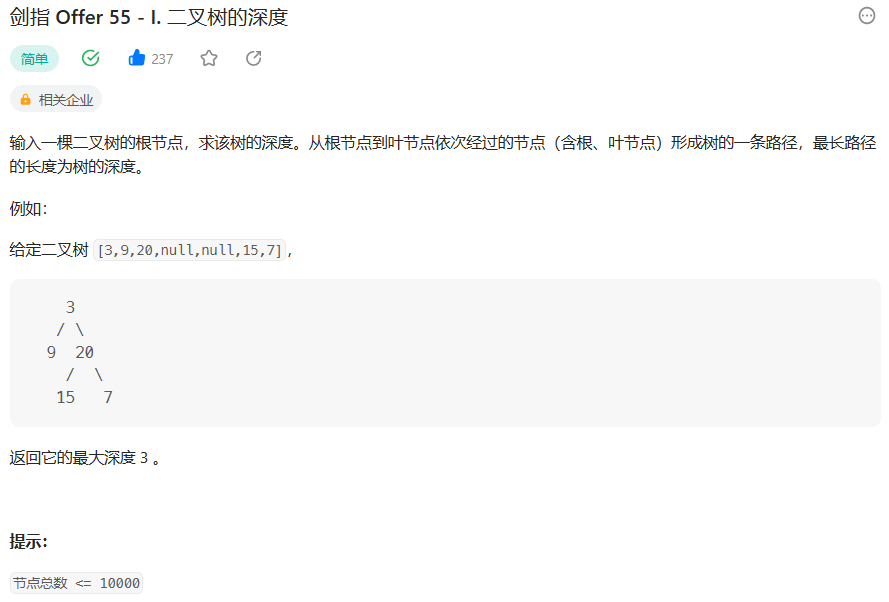
题目的接口:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int maxDepth(TreeNode* root) {
}
};解题思路:
我的思路是,计算每一个子树的左右子树的深度,
然后比较每一个左右子树的深度,保存最大值,
具体解析如图所示:

通过不断计算每个子树的最大深度,
最后得出整棵树的最大深度
下面是代码:
代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int maxDepth(TreeNode* root) {
if(root == nullptr) return 0;
int left = maxDepth(root->left); //求出左边高度
int right = maxDepth(root->right); //求出右边高度
return max(left, right) + 1; //每层 + 1
}
};过啦!!!

题目:剑指 Offer 55 - II. 平衡二叉树 - 力扣(Leetcode)

题目的接口:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
bool isBalanced(TreeNode* root) {
}
};解题思路:
具体思路是,
我们通过计算左右子树的最大深度差,
如果左右子树的最大深度差 >= 2 证明不是平衡二叉树,
如果 < 2 就证明这个子树本身是平衡二叉树,那就正常计算自身的最大深度,
一直到根节点的左右子树依然没有返回 -1 深度符合要求,证明是平衡二叉树,
如果返回了 -1 就证明不是平衡二叉树,
这里计算最大深度的思想也沿用了上一题的思路,
下面是代码:
代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
bool isBalanced(TreeNode* root) {
//判断如果返回-1就证明不是平衡二叉树
return recur(root) != -1;
}
private:
int recur(TreeNode* root) {
if(root == nullptr) return 0;
//计算左右子树最大深度,如果出现-1证明不是平衡二叉树,返回-1就行
int left = recur(root->left);
if(left == -1) return -1;
int right = recur(root->right);
if(right == -1) return -1;
//核心代码:如果左右子树最大深度正常,就正常计算左右深度的最大值
//如果左右子树的最大深度差大于2,就证明这不是一个平衡二叉,返回-1
return abs(left - right) < 2 ? max(left, right) + 1 : -1;
}
};过啦!!!

写在最后:
以上就是本篇文章的内容了,感谢你的阅读。
如果喜欢本文的话,欢迎点赞和评论,写下你的见解。
如果想和我一起学习编程,不妨点个关注,我们一起学习,一同成长。
之后我还会输出更多高质量内容,欢迎收看