一.前言

http://t.csdn.cn/mz8dghttp://t.csdn.cn/mz8dghttp://t.csdn.cn/1TqDphttp://t.csdn.cn/1TqDp

😄关于快排的基本思想和实现及其优化

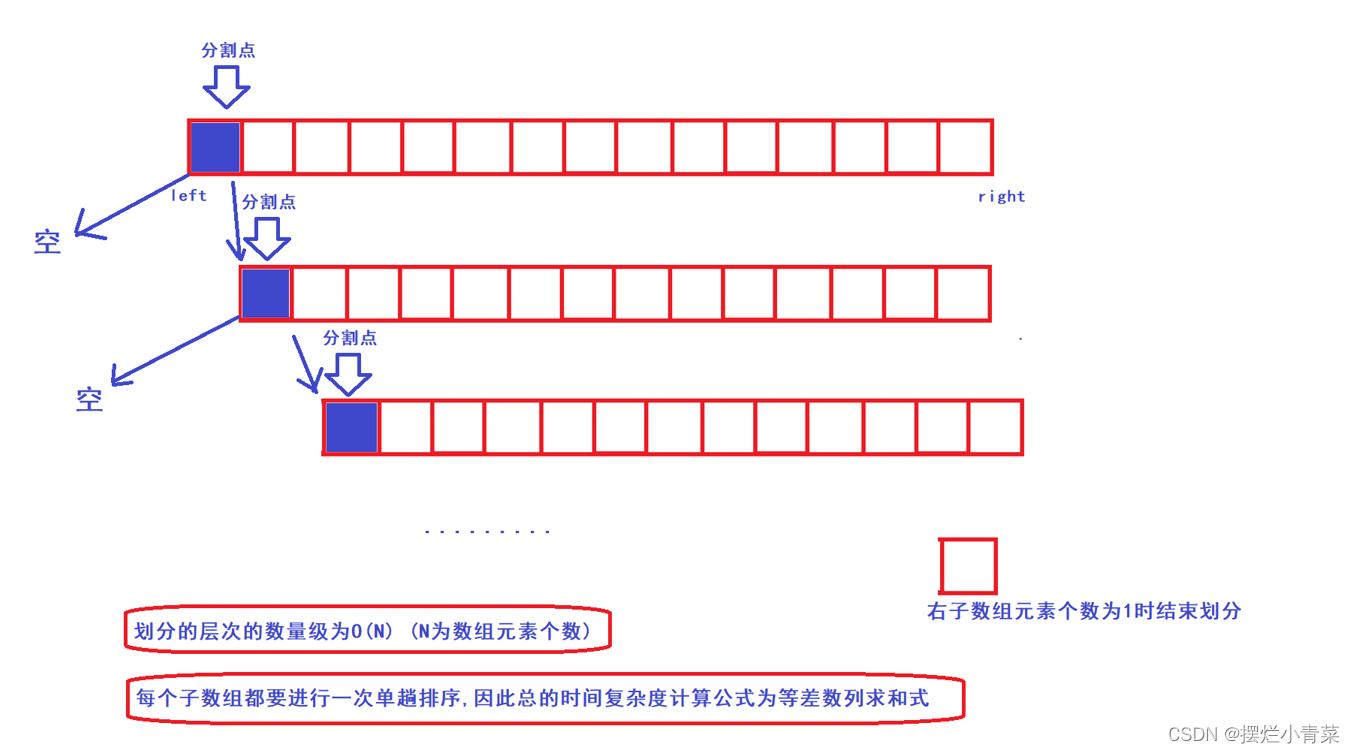
😄利用双指针单趟排序实现的快速排序有一个无法避免的缺陷:当待排序序列中有大量(或全部)元素相同时,快排的时间复杂度会升阶为O(N^2),此时快排的递归树呈线型结构,递归的深度为O(N),时间消耗和空间消耗都非常巨大:
😄为了避免这种情况出现,就需要重新设计一下快排的单趟排序,目的在于:当待排序序列中存在大量相同元素时,减小快排递归树的深度

二. 三路快排

😍算法思想:

🤪三路快排的单趟排序是利用三指针算法来实现的
🤪其基本思想是利用三个指针将数组从左到右划分为三个部分,第一部分中所有元素都比key小,第二部分中所有元素都等于key,第三部分中所有元素都大于key
🤪后续就可以对数组第一部分和第三部分进行分治,数组的第二部分所有元素已经处于它们在有序序列中的最终位置,无须再进行处理
🤪三路快排的边界条件有点折磨人

😍算法实现步骤:

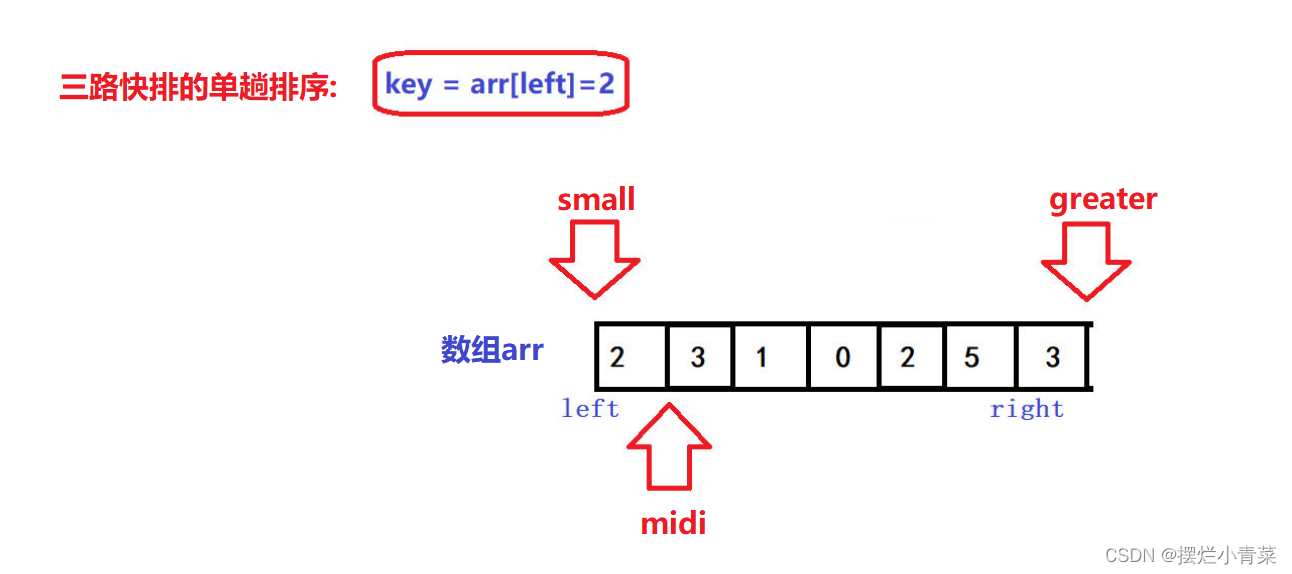
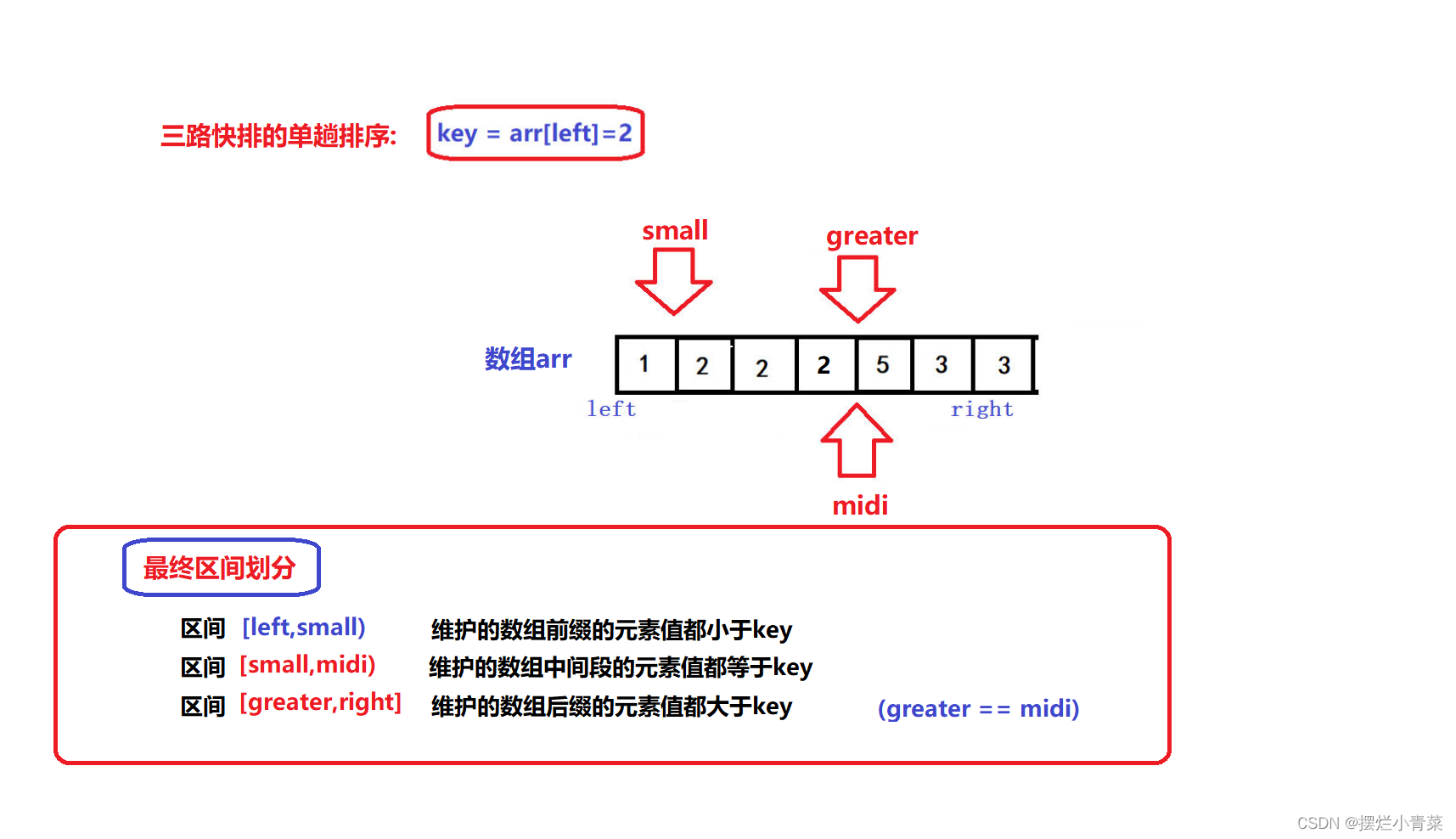
🤪三个指针的初始位置如图所示
🤪left是待排序区间的左边界,right是待排序区间的右边界,待排序区间为闭区间
🤪算法实现思路:
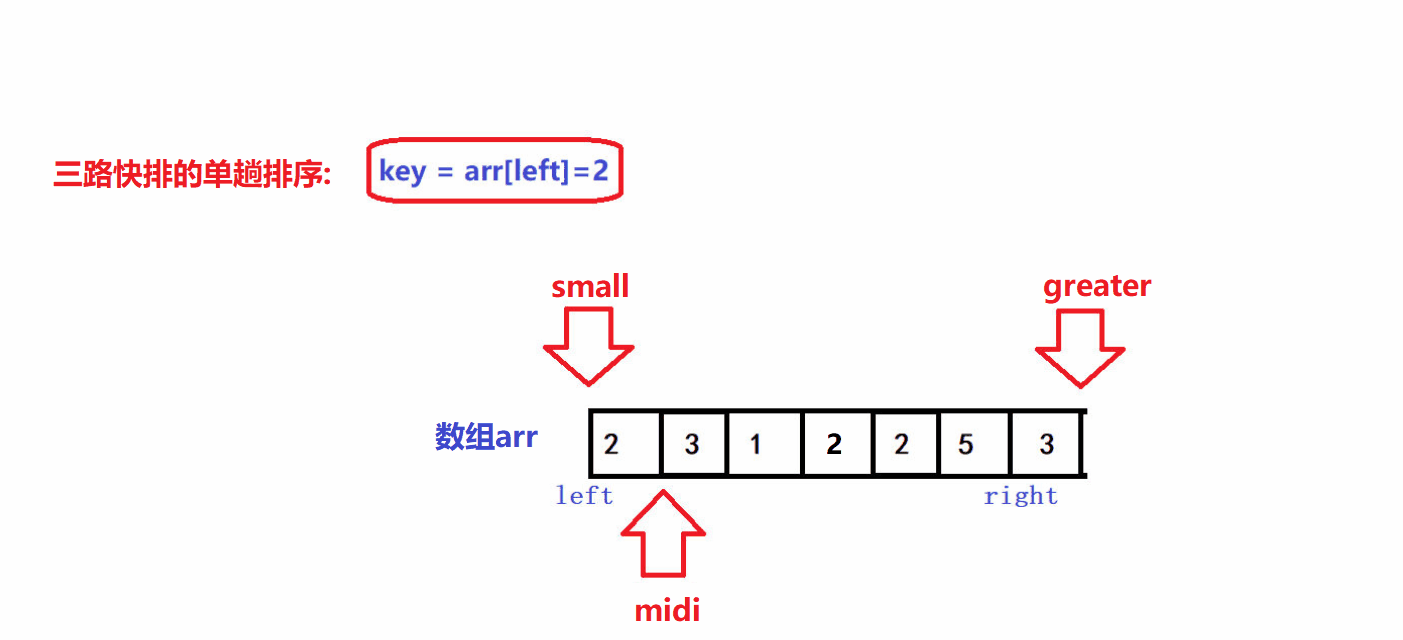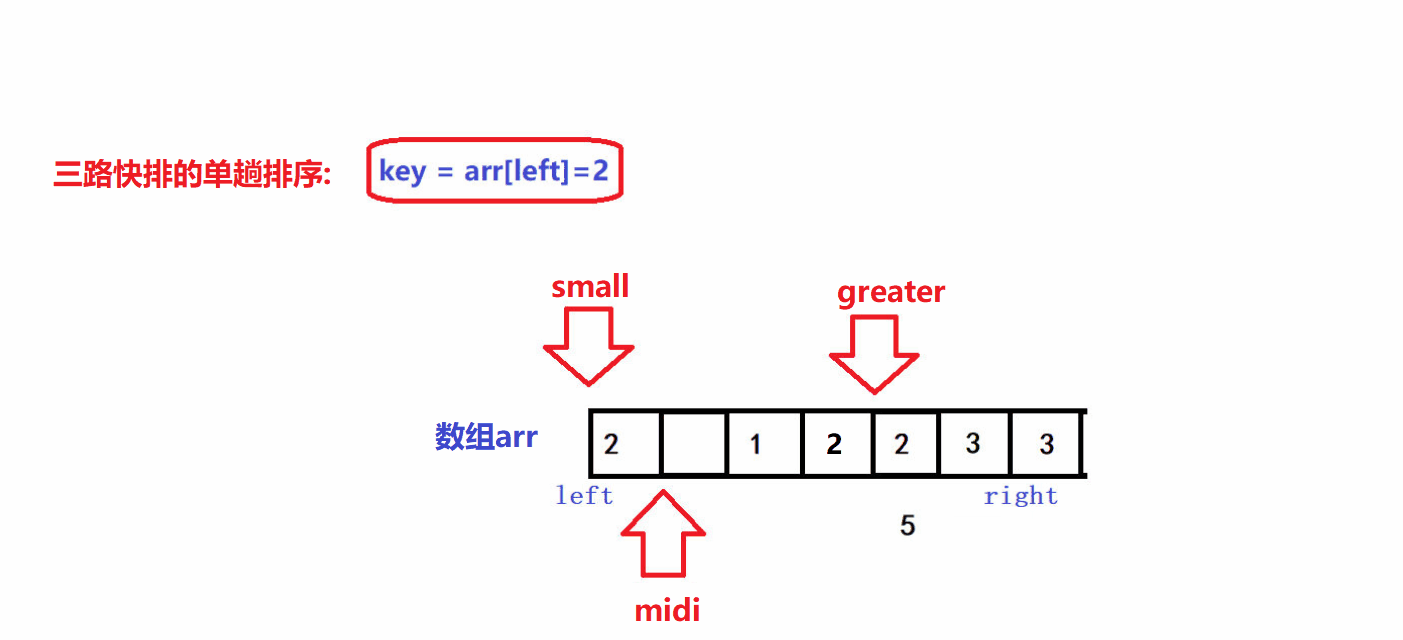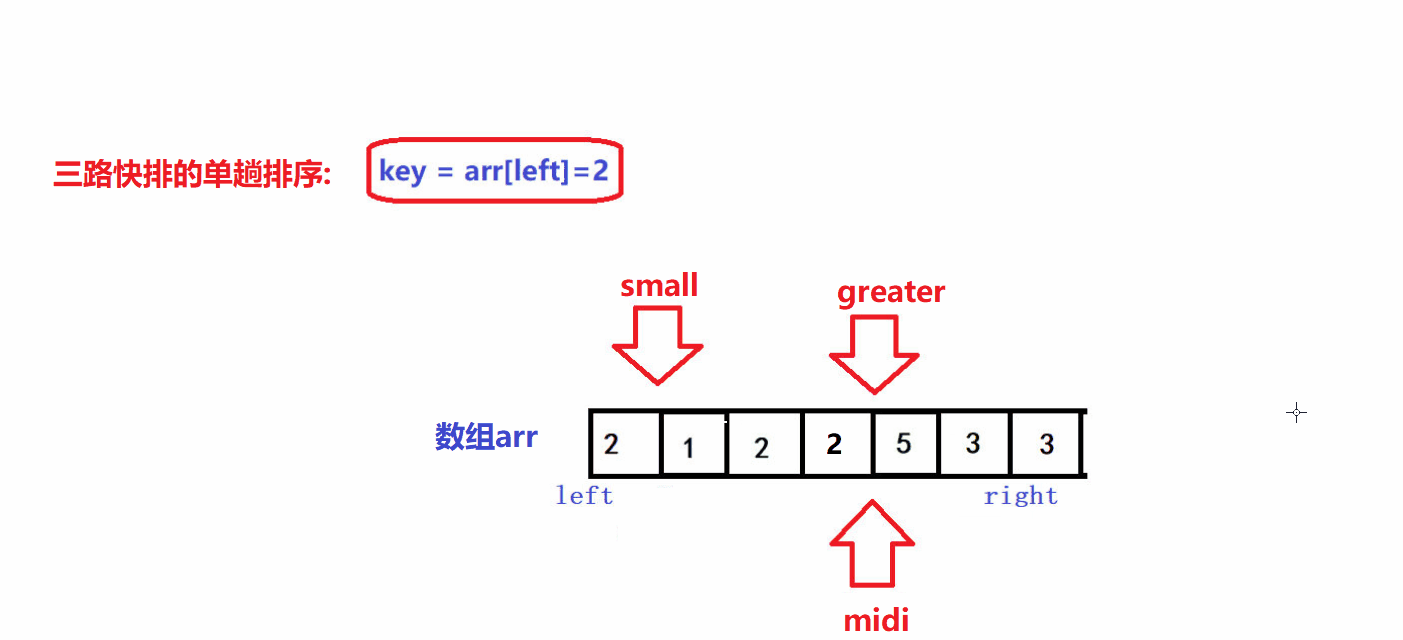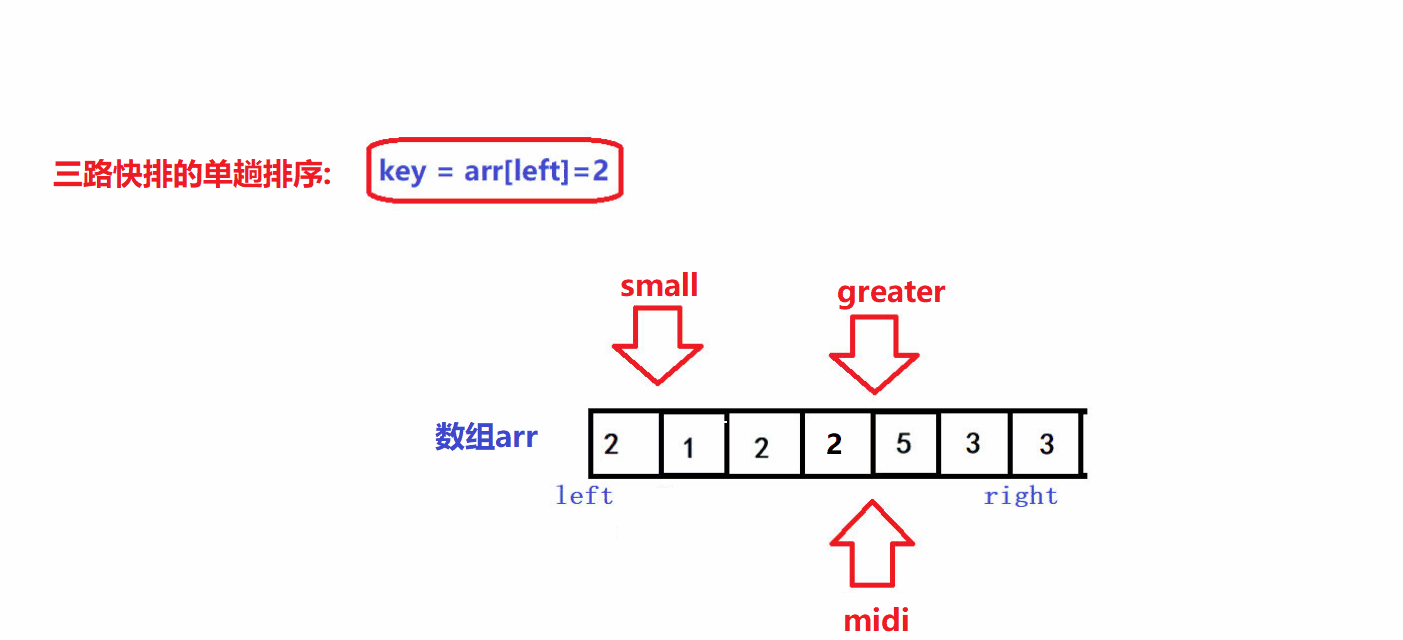
🤪利用midi指针来遍历待排序序列,遍历限制条件为:midi<greater.

😝若arr[midi]比key大,令grater指针减一,并将arr[midi]交换到[greater,right]区间中,midi指针不动
😝若arr[midi]比key小,令small指针加一, 并将arr[midi]交换到[left+1,small]区间中,midi指针向前走一步
😝若arr[midi]与key相同,midi指针向前走一步,其余指针不动,目的是将等于key元素的arr[midi]"括入"[small+1,midi)区间中

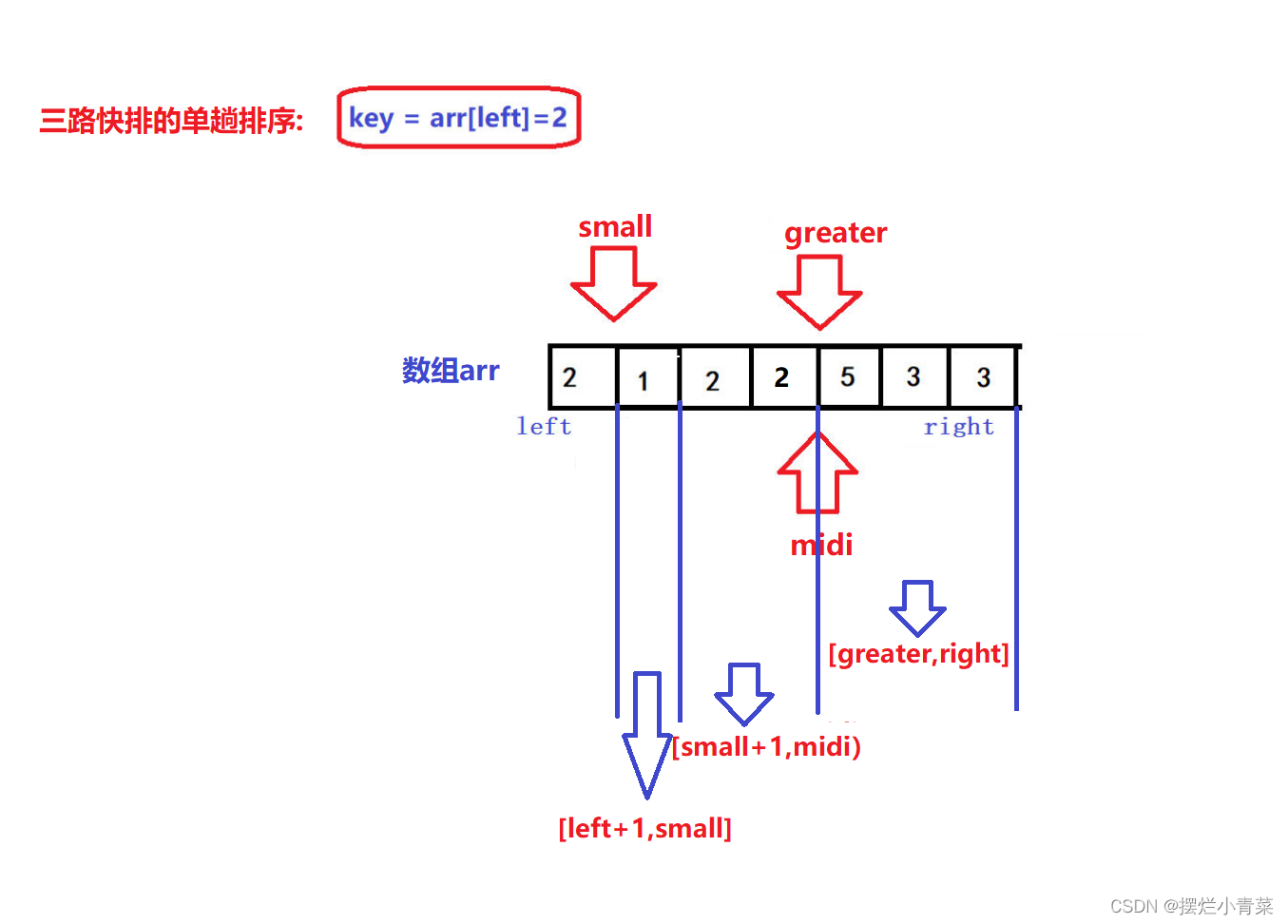
😝重复上述过程直到midi指针和geater指针相遇,算法gif:
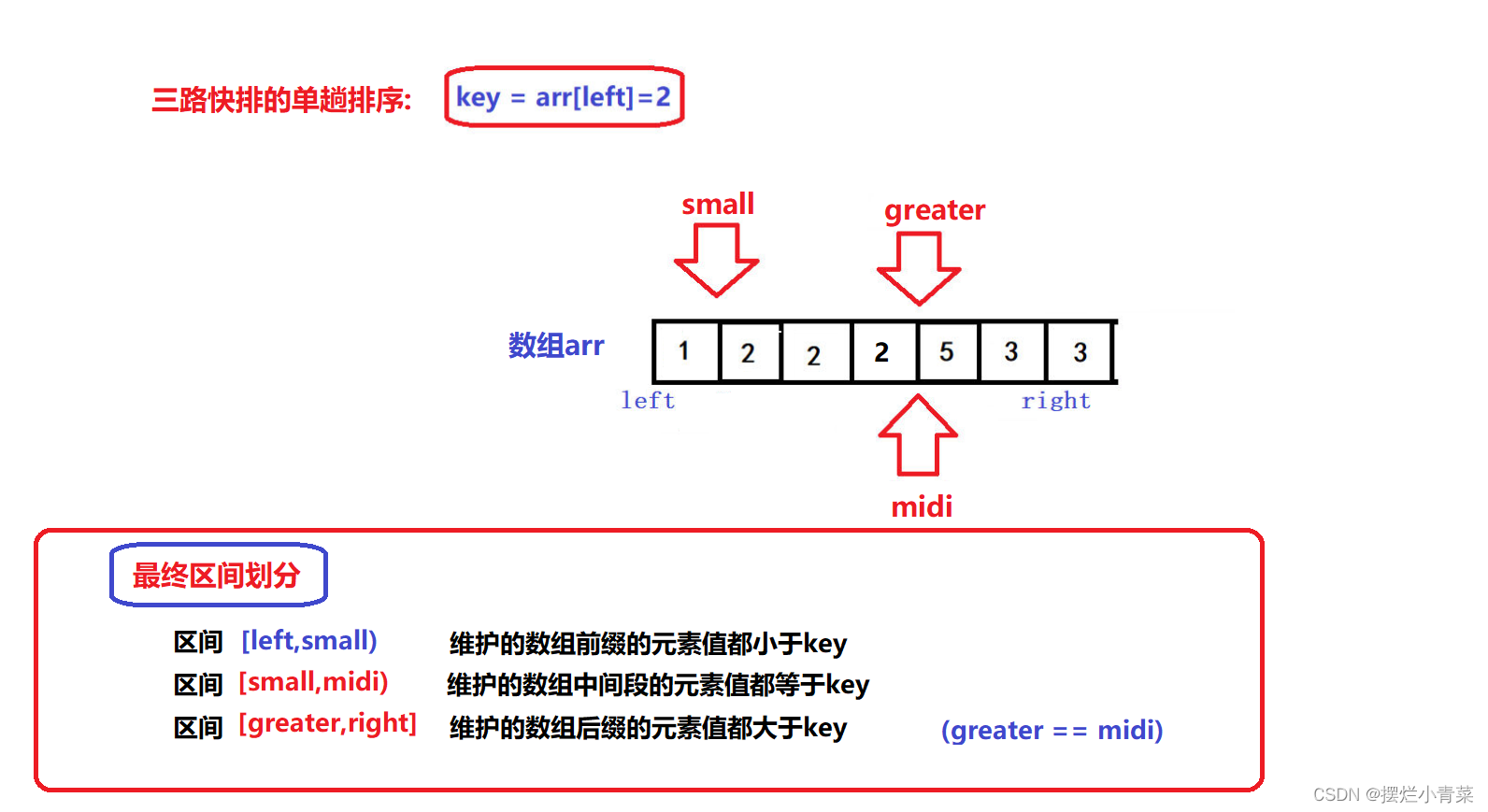
😝经过上述过程,最终[left+1,small]区间中的所有元素一定比key小,[greater,right]区间中的所有元素一定比key大,[small+1,midi)区间中的所有元素一定等于key:
😝同时注意,迭代过程结束后,small最终指向的元素一定小于key,所以最后一步就是将arr[small]和arr[left]进行交换,于是数组就被划分成了三个部分:
😝接下来就可以对区间[left,small-1]和区间[greater,right]进行分治并形成递归完成快速排序

😍三指针单趟排序的实现:

void QuickSort(int* arr, int left, int right)
{
	assert(arr);
	int key = left;
	int midi = left + 1;
	int small = left;
	int greater = right + 1;
	while (midi < greater)
	{
		if (arr[midi] < arr[key])	   //将arr[midi]交换到[left + 1, small]区间中,同时注意small位置的元素一定比key元素小
		{
			++small;
			if (small != midi)
			{
				swap(&arr[small], &arr[midi]);
			}
			++midi;
		}
		else if (arr[midi] > arr[key]) //将arr[midi]交换到[greater,right]区间
		{
			--greater;
			swap(&arr[midi], &arr[greater]);
		}
		else
		{
			++midi;					   //将等于key元素的arr[midi]"括入"[small+1,midi)区间中
		}
	}
	swap(&arr[small], &arr[key]);      //small最终指向的元素一定小于key
}

接下来再进行分治递归并给出递归出口完成快速排序:

😍非递归快排完全体:

😝同时辅以三数取中优化

void swap(int* e1, int* e2)
{
	assert(e1 && e2);
	int tem = *e1;
	*e1 = *e2;
	*e2 = tem;
}

//三数取中优化
int GetMid(int* arr,int left,int right)
{
	int mid = left + ((right - left) >> 2);     //在arr[left],arr[mid],arr[right]三者中取中间值作为key,返回key的下标
	if (arr[left] < arr[right])
	{
		if (arr[left] < arr[mid] && arr[mid] < arr[right])
		{
			return mid;
		}
		else if (arr[mid] > arr[right])
		{
			return right;
		}
		else
		{
			return left;
		}
	}
	else
	{
		if (arr[left] > arr[mid] && arr[mid] > arr[right])
		{
			return mid;
		}
		else if (arr[mid] > arr[left])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
}
void QuickSort(int* arr, int left, int right)
{
	if (left >= right)                 //递归出口
	{
		return;
	}
	assert(arr);
	int key = left;
    swap(&arr[left], &arr[GetMid(arr, left, right)]);
	int midi = left + 1;
	int small = left;
	int greater = right + 1;
	while (midi < greater)
	{
		if (arr[midi] < arr[key])	   //将arr[midi]交换到[left + 1, small]区间中,同时注意small位置的元素一定比key元素小
		{
			++small;
			if (small != midi)
			{
				swap(&arr[small], &arr[midi]);
			}
			++midi;
		}
		else if (arr[midi] > arr[key]) //将arr[midi]交换到[greater,right]区间
		{
			--greater;
			swap(&arr[midi], &arr[greater]);
		}
		else
		{
			++midi;					   //将等于key元素的arr[midi]"括入"[small+1,midi)区间中
		}
	}
	//small指向的元素一定小于key
	swap(&arr[small], &arr[key]);      //将key交换到其应该出现的最终位置
	QuickSort(arr, left, small - 1);   //分治左子数组
	QuickSort(arr, midi,right);		   //分治右子数组
}

🤔经过三数取中和三指针优化后的快排就可以对任意序列进行高效排序,不会再出现时间复杂度升阶为O(N^2)的情况
🤔力扣排序测试:(该测试非常针对未经优化和非三指针的快排)912. 排序数组 - 力扣（Leetcode）https://leetcode.cn/problems/sort-an-array/description/

🤔与C标准库里的快排进行对比测试:

int main()
{
    srand((unsigned int)time(0));
	const int N = 10000000;
	int* arr1 = (int*)malloc(sizeof(int) * N);
	int* arr2 = (int*)malloc(sizeof(int) * N);
	int* arr3 = (int*)malloc(sizeof(int) * N);
	for (int i = 0; i < N; ++i)
	{
		arr1[i] = rand();
		arr2[i] = arr1[i];
		arr3[i] = arr1[i];
	}

	int begin2 = clock();
	qsort(arr2, N, sizeof(int), cmp);
	int end2 = clock();
	printf("qsort:%d\n", end2 - begin2);

	int begin3 = clock();
	QuickSort(arr3, 0,N-1);
	int end3 = clock();
	printf("QuickSort:%d\n", end3 - begin3);
    
    free(arr1);
    free(arr2);
    free(arr3);
}

🤔有点奇怪的是在我的机器环境中,我自己写的快排比标准库里的快排还要快一倍左右(可执行程序为release版本)

三.快排时间复杂度再分析

😍设N为待排序序列的元素个数
😍以下分析中的log都表示以2为底的对数
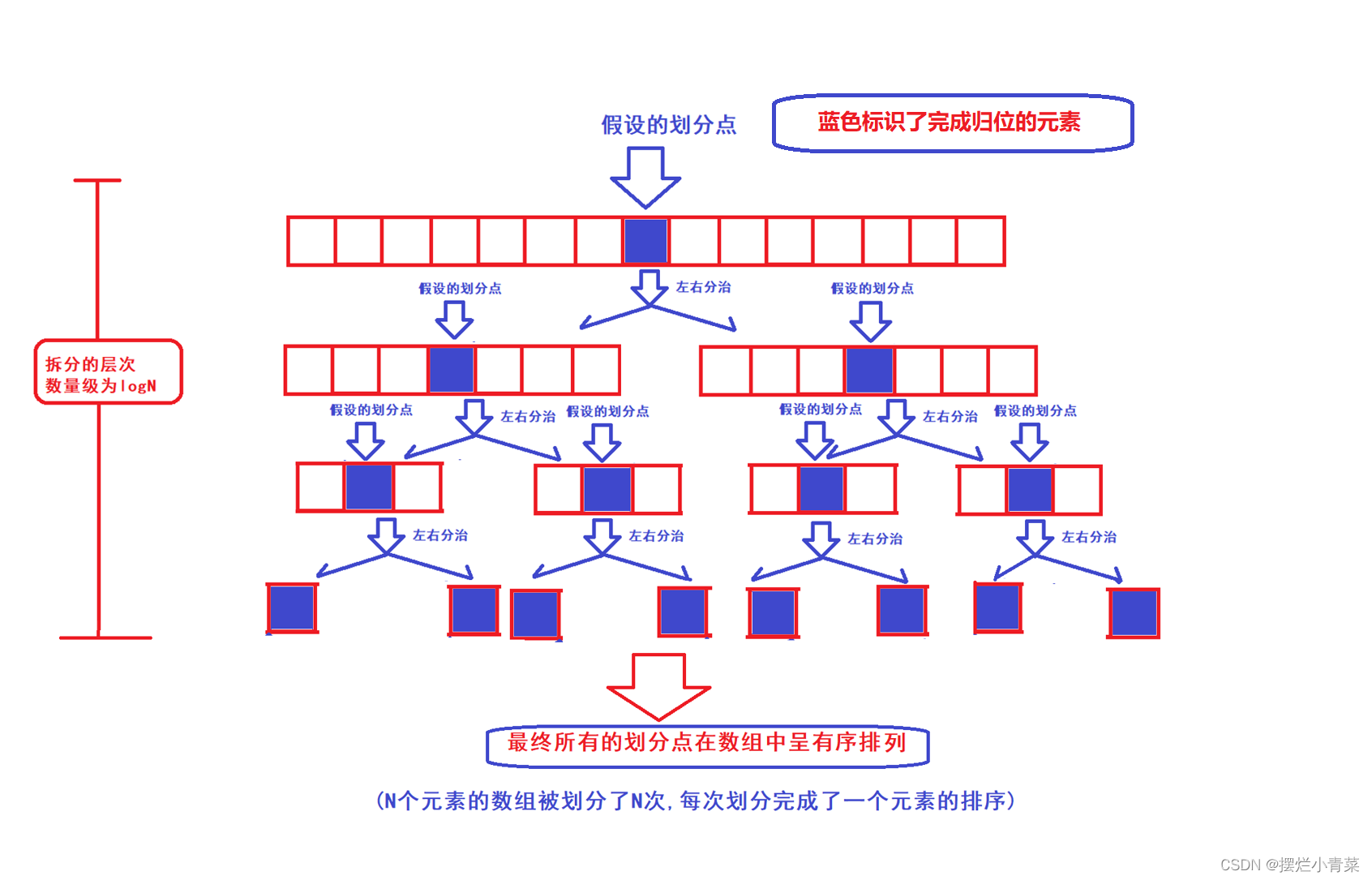
😍经过三数取中和三指针优化后的快排分治递归的递归树可以认为在处理任何序列时都接近一颗满二叉树:(注意数组的分割点不参与后续的单趟排序)
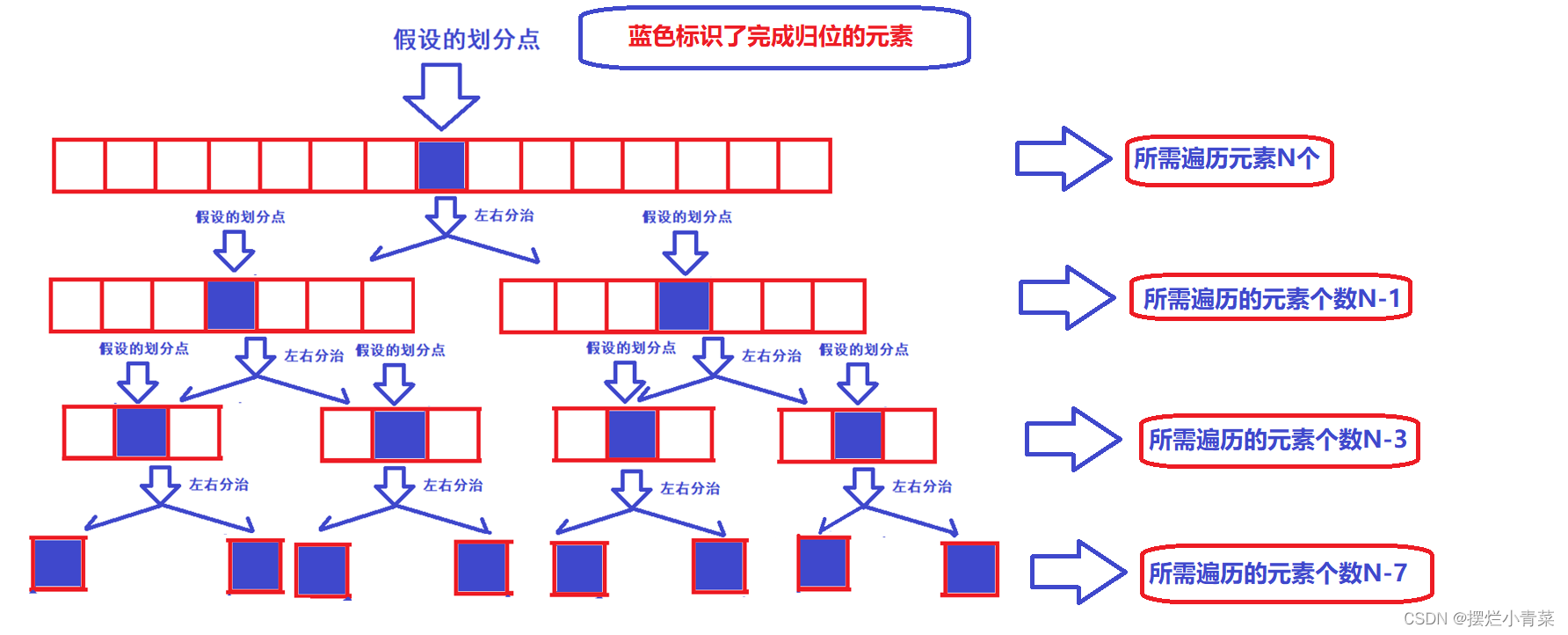
😍从递归树的第一层开始,递归树每一层中所有单趟排序所需遍历元素的总个数依次为:N+(N-1)+(N-3)+(N-7)......即快排的时间复杂度计算公式为:
😍将上述复杂度公式进行求和运算,取b = logN可得:
😍再化简可得:
😍可见快速排序的时间复杂度在O(NlogN)的基础上存在进一步的微收敛,这使得快速排序在四个时间复杂度数量级为O(NlogN)的排序算法中独占鳌头进而成为工业级排序中用的最多的排序算法。(四个时间复杂度为O(NlogN)数量级的排序算法分别为:希尔排序,堆排序,归并排序和快速排序)