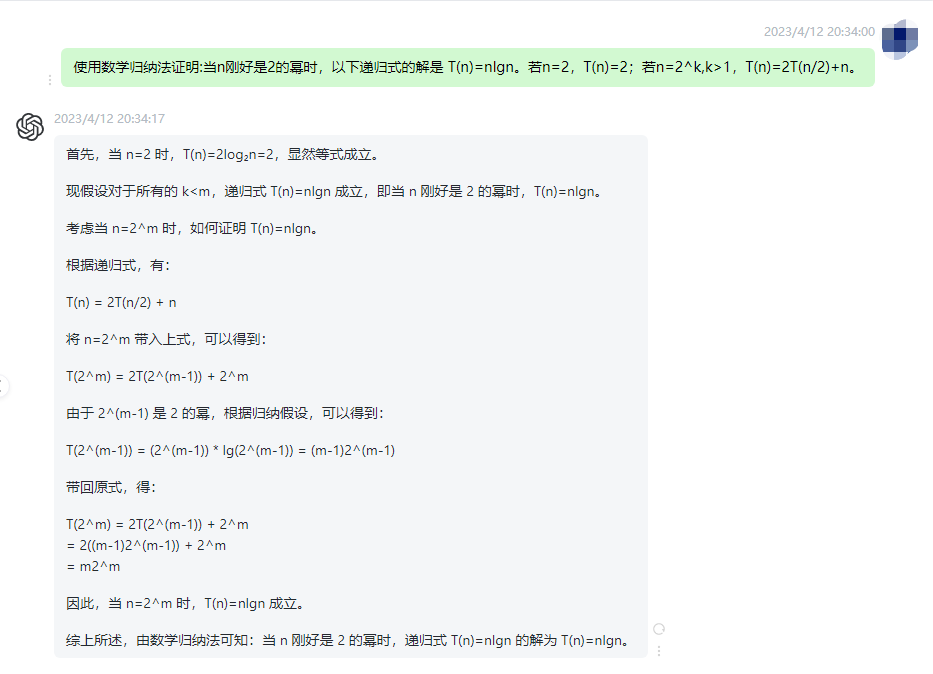
三、使用数学归纳法证明:当n刚好是2的幂时,以下递归式的解是 T(n)=nlgn。若n=2,T(n)=2;若n=2^k,k>1,T(n)=2T(n/2)+n。
文心一言:

chatgpt:
首先,当 n=2 时,T(n)=2log₂n=2,显然等式成立。
现假设对于所有的 k<m,递归式 T(n)=nlgn 成立,即当 n 刚好是 2 的幂时,T(n)=nlgn。
考虑当 n=2^m 时,如何证明 T(n)=nlgn。
根据递归式,有:
T(n) = 2T(n/2) + n
将 n=2^m 带入上式,可以得到:
T(2^m) = 2T(2^(m-1)) + 2^m
由于 2^(m-1) 是 2 的幂,根据归纳假设,可以得到:
T(2^(m-1)) = (2^(m-1)) * lg(2^(m-1)) = (m-1)2^(m-1)
带回原式,得:
T(2^m) = 2T(2^(m-1)) + 2^m
= 2((m-1)2^(m-1)) + 2^m
= m2^m
因此,当 n=2^m 时,T(n)=nlgn 成立。
综上所述,由数学归纳法可知:当 n 刚好是 2 的幂时,递归式 T(n)=nlgn 的解为 T(n)=nlgn。
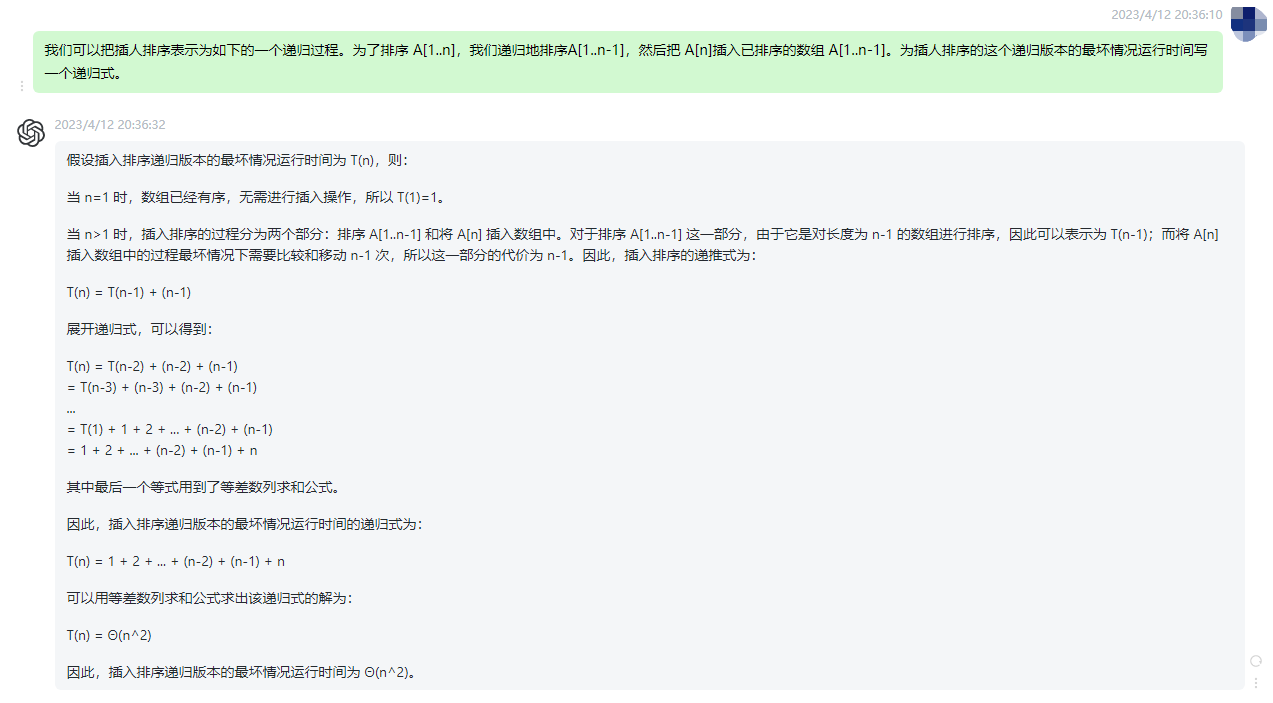
四、我们可以把插人排序表示为如下的一个递归过程。为了排序 A[1…n],我们递归地排序A[1…n-1],然后把 A[n]插入已排序的数组 A[1…n-1]。为插人排序的这个递归版本的最坏情况运行时间写一个递归式。
文心一言:
为了排序 A[1…n],我们递归地排序A[1…n-1],然后把 A[n]插入已排序的数组 A[1…n-1]。为插人排序的这个递归版本的最坏情况运行时间写一个递归式。
最坏情况下,我们需要遍历整个数组,因此递归深度为 n。在每个递归步骤中,我们需要检查是否需要插入新元素,因此递归深度为 n-1。因此,插入排序的最坏情况运行时间为 O(n^2)。

chatgpt:
假设插入排序递归版本的最坏情况运行时间为 T(n),则:
当 n=1 时,数组已经有序,无需进行插入操作,所以 T(1)=1。
当 n>1 时,插入排序的过程分为两个部分:排序 A[1…n-1] 和将 A[n] 插入数组中。对于排序 A[1…n-1] 这一部分,由于它是对长度为 n-1 的数组进行排序,因此可以表示为 T(n-1);而将 A[n] 插入数组中的过程最坏情况下需要比较和移动 n-1 次,所以这一部分的代价为 n-1。因此,插入排序的递推式为:
T(n) = T(n-1) + (n-1)
展开递归式,可以得到:
T(n) = T(n-2) + (n-2) + (n-1)
= T(n-3) + (n-3) + (n-2) + (n-1)
…
= T(1) + 1 + 2 + … + (n-2) + (n-1)
= 1 + 2 + … + (n-2) + (n-1) + n
其中最后一个等式用到了等差数列求和公式。
因此,插入排序递归版本的最坏情况运行时间的递归式为:
T(n) = 1 + 2 + … + (n-2) + (n-1) + n
可以用等差数列求和公式求出该递归式的解为:
T(n) = Θ(n^2)
因此,插入排序递归版本的最坏情况运行时间为 Θ(n^2)。