Bezier Curve 贝塞尔曲线 - 在Unity中实现路径编辑

news2025/1/17 18:10:44

文章目录

  • 简介
    • 一阶贝塞尔曲线
    • 二阶贝塞尔曲线
    • 三阶贝塞尔曲线
  • 图形理解 Bezier Curve
    • 一阶贝塞尔曲线
    • 二阶贝塞尔曲线
    • 三阶贝塞尔曲线
  • 应用
    • Bezier Curve
    • SimpleBezierCurvePath
    • SimpleBezierCurvePathAlonger

简介

贝塞尔曲线（Bezier Curve），又称贝兹曲线或贝济埃曲线，是计算机图形学中相当重要的参数曲线，在我们常用的软件如Photo Shop中就有贝塞尔曲线工具，本文简单介绍贝塞尔曲线在Unity中的实现与应用。

一阶贝塞尔曲线

给顶点P0、P1，只是一条两点之间的直线，公式如下：

B(t) = P0 + (P1 - P0) t = (1 - t) P0 + t P1, t ∈ [0, 1]

等同于线性插值，代码实现如下：

/// <summary>
/// 一阶贝塞尔曲线
/// </summary>
/// <param name="p0">起点</param>
/// <param name="p1">终点</param>
/// <param name="t">[0,1]</param>
/// <returns></returns>
public static Vector3 Bezier1(Vector3 p0, Vector3 p1, float t)
{
    return (1 - t) * p0 + t * p1;
}

二阶贝塞尔曲线

路径由给定点P0、P1、P2的函数计算，公式如下：

B(t) = (1 - t)2 P0 + 2t (1 - t) P1 + t2P2, t ∈[0, 1]

代码实现如下：

/// <summary>
/// 二阶贝塞尔曲线
/// </summary>
/// <param name="p0">起点</param>
/// <param name="p1">控制点</param>
/// <param name="p2">终点</param>
/// <param name="t">[0,1]</param>
/// <returns></returns>
public static Vector3 Bezier2(Vector3 p0, Vector3 p1, Vector3 p2, float t)
{
    Vector3 p0p1 = (1 - t) * p0 + t * p1;
    Vector3 p1p2 = (1 - t) * p1 + t * p2;
    return (1 - t) * p0p1 + t * p1p2;
}

三阶贝塞尔曲线

P0、P1、P2、P3四个点在平面或三维空间中定义了三次方贝塞尔曲线。曲线起始于P0走向P1，并从P2的方向来到P3，一般不会经过P1、P2，这两个点只是提供方向信息，可以将P1、P2理解为控制点。P0和P1之间的间距，决定了曲线在转而趋近P3之前，走向P2的长度有多长，公式如下：

B(t) = P0(1 - t)3 + 3P1t(1 - t)2 + 3P2t2(1 - t) + P3t3, t ∈ [0, 1]

代码实现如下：

/// <summary>
/// 三阶贝塞尔曲线
/// </summary>
/// <param name="p0">起点</param>
/// <param name="p1">控制点1</param>
/// <param name="p2">控制点2</param>
/// <param name="p3">终点</param>
/// <param name="t">[0,1]</param>
/// <returns></returns>
public static Vector3 Bezier3(Vector3 p0, Vector3 p1, Vector3 p2, Vector3 p3, float t)
{
    Vector3 p0p1 = (1 - t) * p0 + t * p1;
    Vector3 p1p2 = (1 - t) * p1 + t * p2;
    Vector3 p2p3 = (1 - t) * p2 + t * p3;
    Vector3 p0p1p2 = (1 - t) * p0p1 + t * p1p2;
    Vector3 p1p2p3 = (1 - t) * p1p2 + t * p2p3;
    return (1 - t) * p0p1p2 + t * p1p2p3;
}

图形理解 Bezier Curve

使用Gizmos绘制Bezier Curve，通过图形理解贝塞尔曲线：

一阶贝塞尔曲线

P0为起点，P1为终点，t从0到1时，在贝塞尔曲线上对应的点为Pt，可以将t为理解为动画播放中的normalized time

一阶贝塞尔曲线

代码如下：

using UnityEngine;
using SK.Framework;

#if UNITY_EDITOR
using UnityEditor;
#endif

public class Example : MonoBehaviour
{
    private float t;

    private void Update()
    {
        if (t < 1f)
        {
            t += Time.deltaTime * .2f;
            t = Mathf.Clamp01(t);
        }
    }

#if UNITY_EDITOR
    private void OnDrawGizmos()
    {
        Gizmos.color = Color.grey;
        Vector3 p0 = Vector3.left * 5f;
        Vector3 p1 = Vector3.right * 5f;
        Gizmos.DrawLine(p0, p1);
        Handles.Label(p0, "P0");
        Handles.Label(p1, "P1");
        Handles.SphereHandleCap(0, p0, Quaternion.identity, .1f, EventType.Repaint);
        Handles.SphereHandleCap(0, p1, Quaternion.identity, .1f, EventType.Repaint);
        Vector3 pt = BezierCurveUtility.Bezier1(p0, p1, t);
        Gizmos.color = Color.red;
        Gizmos.DrawLine(p0, pt);
        Handles.Label(pt, string.Format("Pt (t = {0})", t));
        Handles.SphereHandleCap(0, pt, Quaternion.identity, .1f, EventType.Repaint);
    }
#endif
}

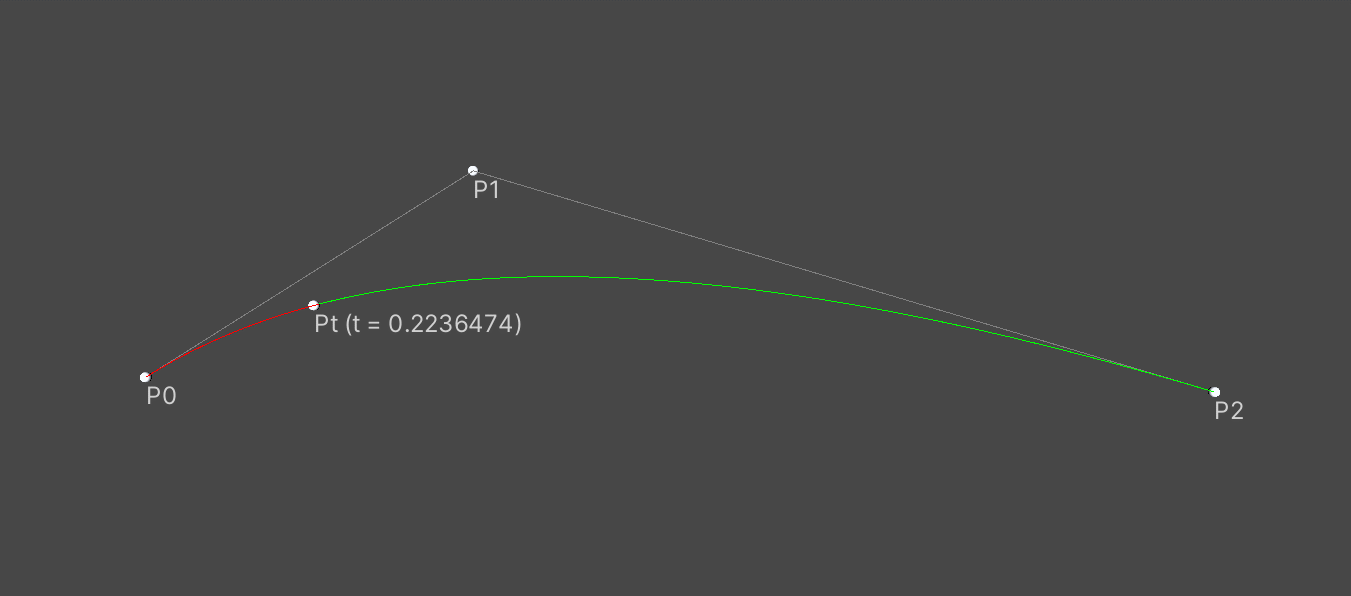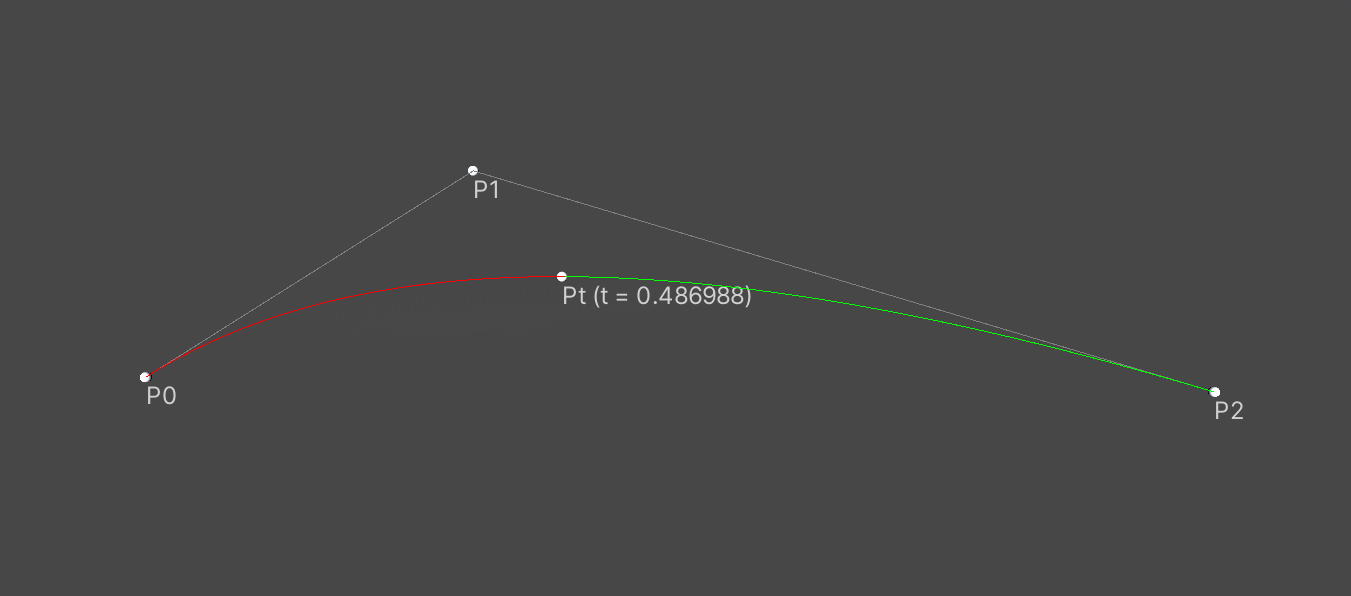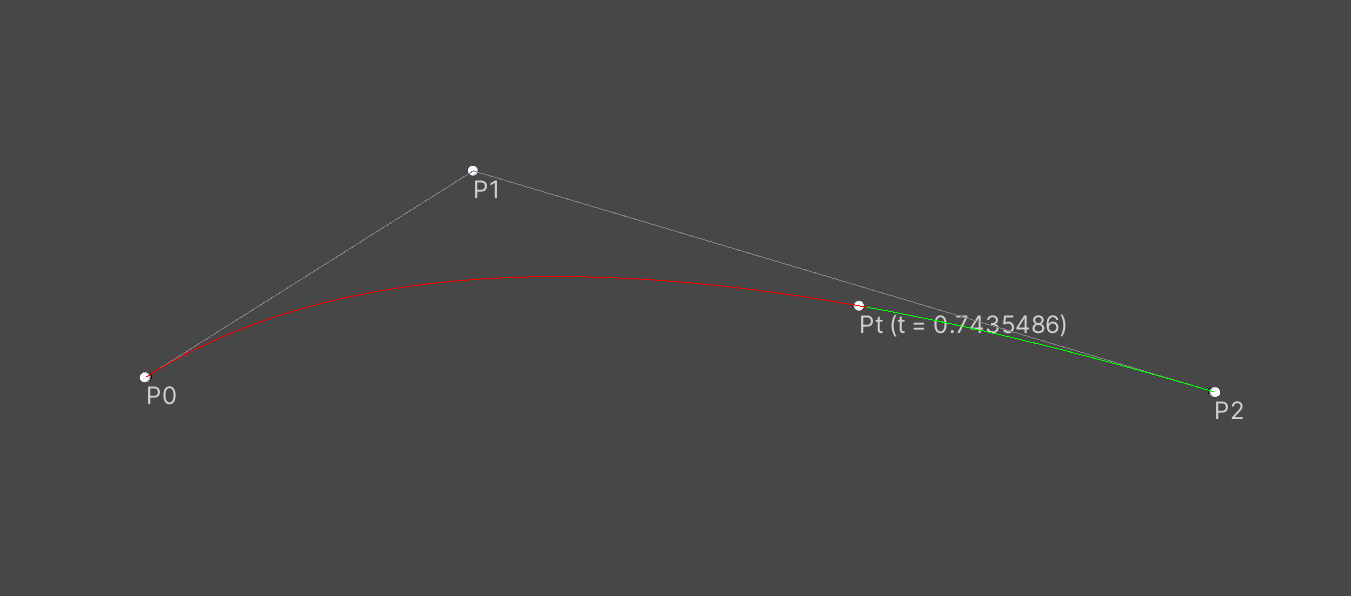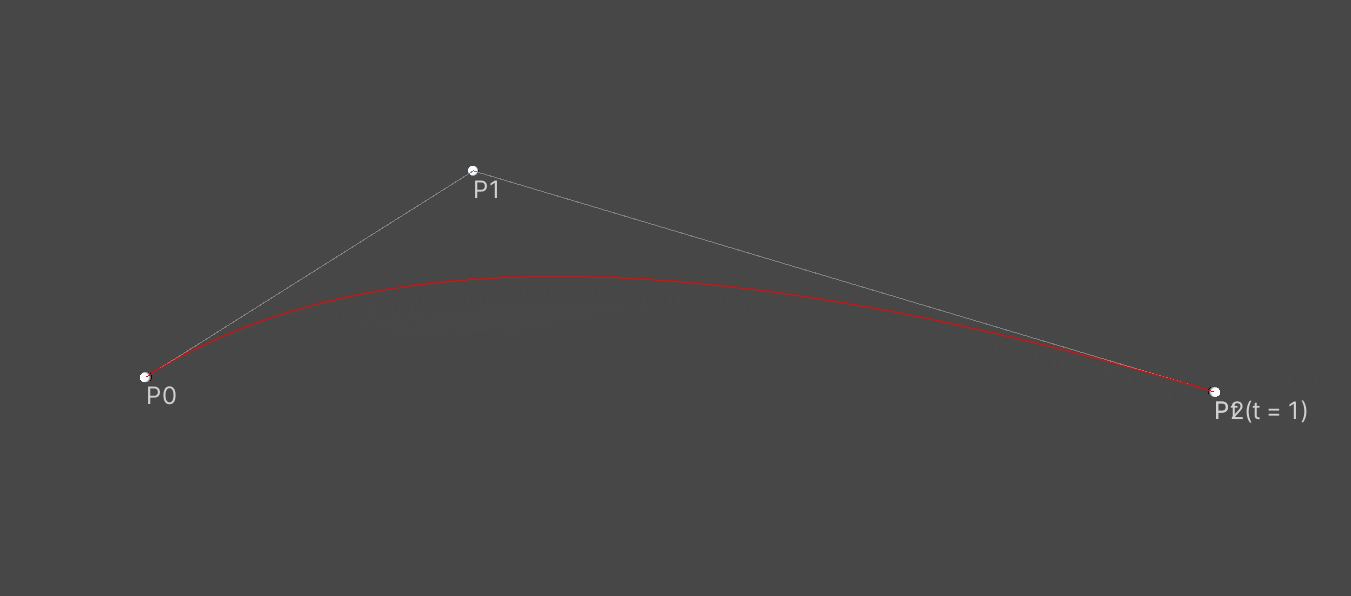
二阶贝塞尔曲线

P0为起点，P1为控制点，P2为终点，t从0到1时，在贝塞尔曲线上对应的点为Pt

二阶贝塞尔曲线

代码如下：

using UnityEngine;
using SK.Framework;

#if UNITY_EDITOR
using UnityEditor;
#endif

public class Example : MonoBehaviour
{
    private float t;

    private void Update()
    {
        if (t < 1f)
        {
            t += Time.deltaTime * .2f;
            t = Mathf.Clamp01(t);
        }
    }

#if UNITY_EDITOR
    private void OnDrawGizmos()
    {
        Gizmos.color = Color.grey;
        Vector3 p0 = Vector3.left * 5f;
        Vector3 p1 = Vector3.left * 2f + Vector3.forward * 2f;
        Vector3 p2 = Vector3.right * 5f;
        Gizmos.DrawLine(p0, p1);
        Gizmos.DrawLine(p2, p1);
        Handles.Label(p0, "P0");
        Handles.Label(p1, "P1");
        Handles.Label(p2, "P2");
        Handles.SphereHandleCap(0, p0, Quaternion.identity, .1f, EventType.Repaint);
        Handles.SphereHandleCap(0, p1, Quaternion.identity, .1f, EventType.Repaint);
        Handles.SphereHandleCap(0, p2, Quaternion.identity, .1f, EventType.Repaint);

        Gizmos.color = Color.green;
        for (int i = 0; i < 100; i++)
        {
            Vector3 curr = BezierCurveUtility.Bezier2(p0, p1, p2, i / 100f);
            Vector3 next = BezierCurveUtility.Bezier2(p0, p1, p2, (i + 1) / 100f);
            Gizmos.color = t > (i / 100f) ? Color.red : Color.green;
            Gizmos.DrawLine(curr, next);
        }
        Vector3 pt = BezierCurveUtility.Bezier2(p0, p1, p2, t);
        Handles.Label(pt, string.Format("Pt (t = {0})", t));
        Handles.SphereHandleCap(0, pt, Quaternion.identity, .1f, EventType.Repaint);
    }
#endif
}

三阶贝塞尔曲线

P0为起点，P1为第一个控制点，P2为第二个控制点，P3为终点，t从0到1时，在贝塞尔曲线上对应的点为Pt

三阶贝塞尔曲线

代码如下：

using UnityEngine;
using SK.Framework;

#if UNITY_EDITOR
using UnityEditor;
#endif

public class Example : MonoBehaviour
{
    private float t;

    private void Update()
    {
        if (t < 1f)
        {
            t += Time.deltaTime * .2f;
            t = Mathf.Clamp01(t);
        }
    }

#if UNITY_EDITOR
    private void OnDrawGizmos()
    {
        Gizmos.color = Color.grey;
        Vector3 p0 = Vector3.left * 5f;
        Vector3 p1 = Vector3.left * 2f + Vector3.forward * 2f;
        Vector3 p2 = Vector3.right * 3f + Vector3.back * 4f;
        Vector3 p3 = Vector3.right * 5f;
        Gizmos.DrawLine(p0, p1);
        Gizmos.DrawLine(p1, p2);
        Gizmos.DrawLine(p2, p3);
        Handles.Label(p0, "P0");
        Handles.Label(p1, "P1");
        Handles.Label(p2, "P2");
        Handles.Label(p3, "P3");
        Handles.SphereHandleCap(0, p0, Quaternion.identity, .1f, EventType.Repaint);
        Handles.SphereHandleCap(0, p1, Quaternion.identity, .1f, EventType.Repaint);
        Handles.SphereHandleCap(0, p2, Quaternion.identity, .1f, EventType.Repaint);
        Handles.SphereHandleCap(0, p3, Quaternion.identity, .1f, EventType.Repaint);

        Gizmos.color = Color.green;
        for (int i = 0; i < 100; i++)
        {
            Vector3 curr = BezierCurveUtility.Bezier3(p0, p1, p2, p3, i / 100f);
            Vector3 next = BezierCurveUtility.Bezier3(p0, p1, p2, p3, (i + 1) / 100f);
            Gizmos.color = t > (i / 100f) ? Color.red : Color.green;
            Gizmos.DrawLine(curr, next);
        }
        Vector3 pt = BezierCurveUtility.Bezier3(p0, p1, p2, p3, t);
        Handles.Label(pt, string.Format("Pt (t = {0})", t));
        Handles.SphereHandleCap(0, pt, Quaternion.identity, .1f, EventType.Repaint);
    }
#endif
}

应用

常见的如道路编辑、河流编辑功能都可以通过贝塞尔曲线实现：

河流编辑

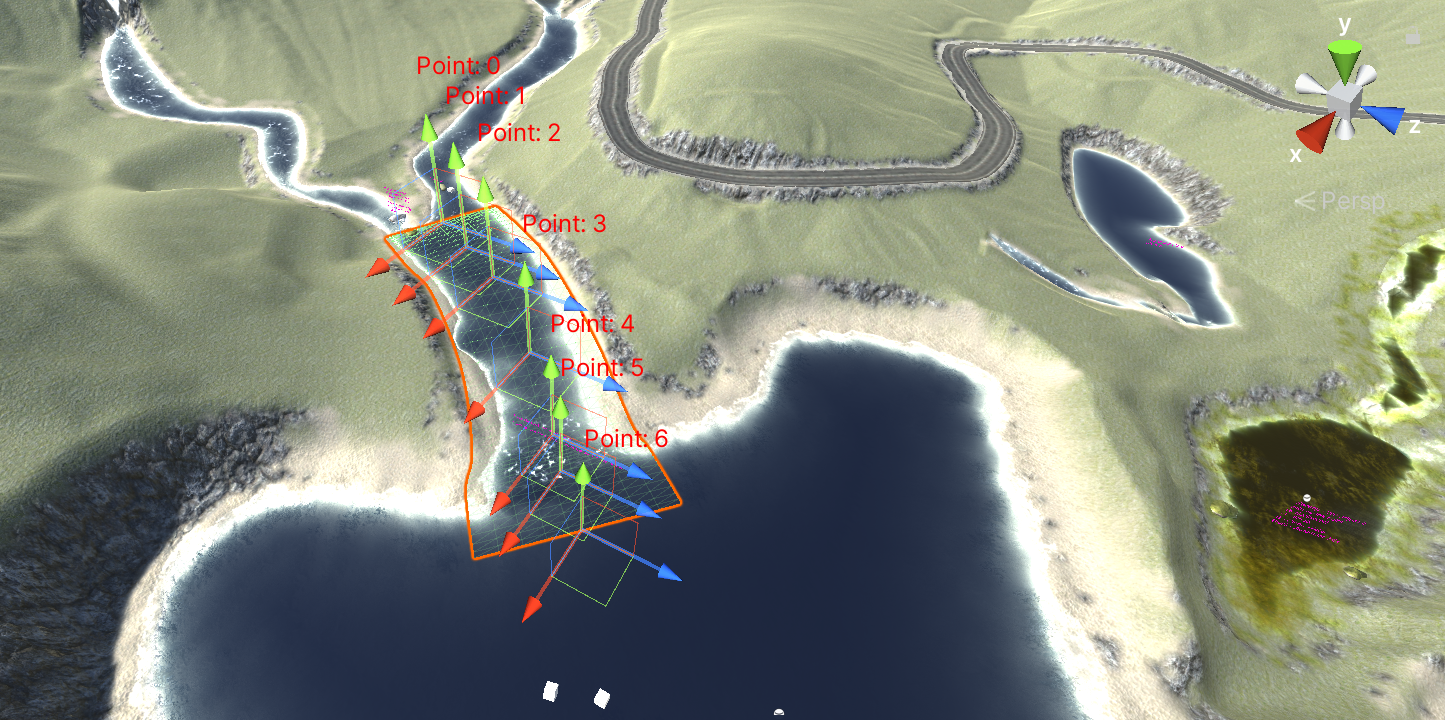
本文以一个简单的路径编辑为例，通过使用三阶贝塞尔曲线实现路径的编辑：

路径编辑

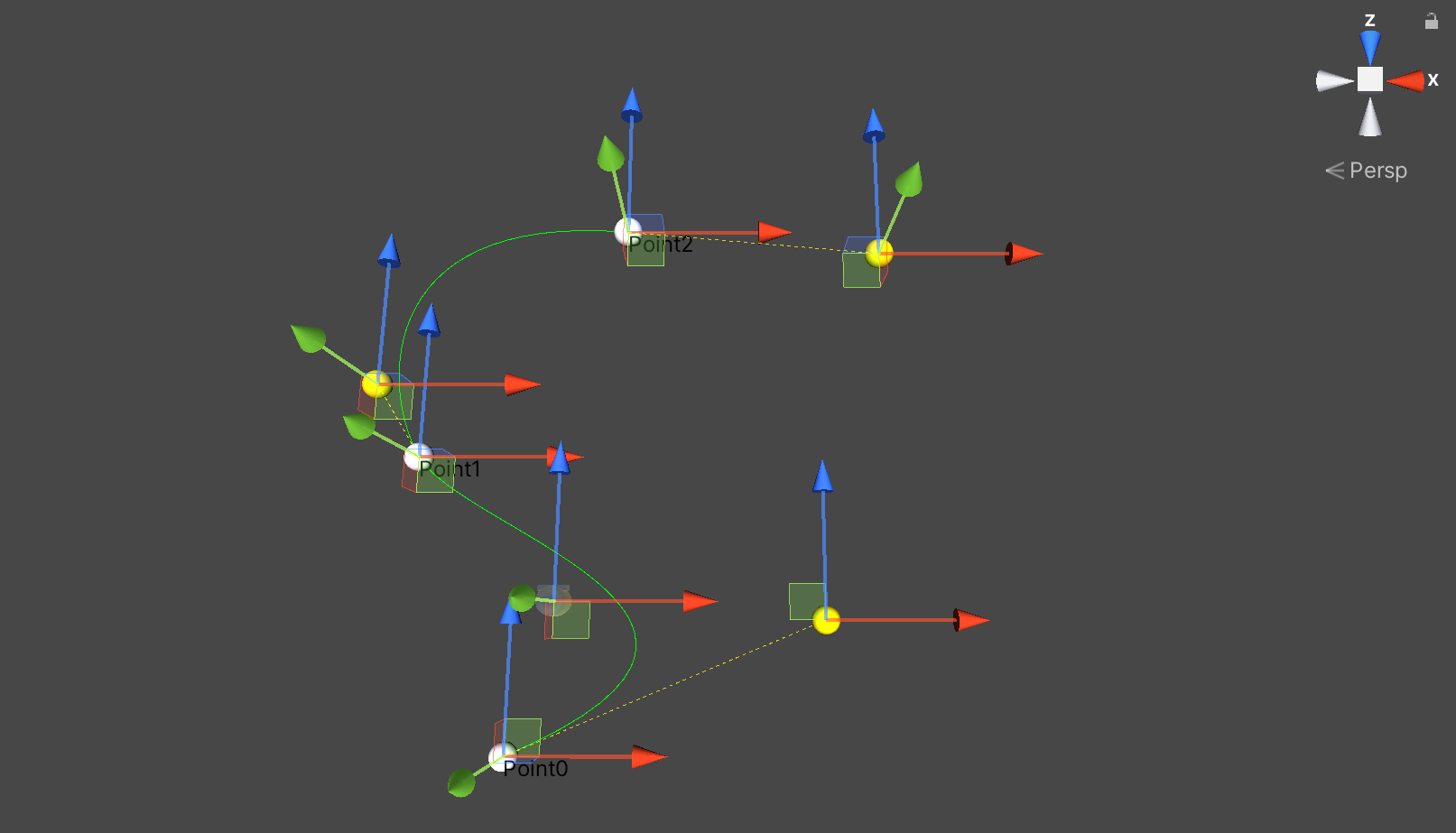
Bezier Curve

  • segments：贝塞尔曲线的段数，值越大曲线精度越高；
  • loop：是否循环（首尾相连）；
  • points ：点集合（结构体中包含坐标点和控制点）；
using System;
using UnityEngine;
using System.Collections.Generic;

namespace SK.Framework
{
    /// <summary>
    /// 贝塞尔曲线
    /// </summary>
    [Serializable]
    public class BezierCurve
    {
        /// <summary>
        /// 段数
        /// </summary>
        [Range(1, 100)] public int segments = 10;

        /// <summary>
        /// 是否循环
        /// </summary>
        public bool loop;

        /// <summary>
        /// 点集合
        /// </summary>
        public List<BezierCurvePoint> points = new List<BezierCurvePoint>(2)
        {
            new BezierCurvePoint() { position = Vector3.back * 5f, tangent = Vector3.back * 5f + Vector3.left * 3f },
            new BezierCurvePoint() { position = Vector3.forward * 5f, tangent = Vector3.forward * 5f + Vector3.right * 3f }
        };

        /// <summary>
        /// 根据归一化位置值获取对应的贝塞尔曲线上的点
        /// </summary>
        /// <param name="t">归一化位置值 [0,1]</param>
        /// <returns></returns>
        public Vector3 EvaluatePosition(float t)
        {
            Vector3 retVal = Vector3.zero;
            if (points.Count > 0)
            {
                float max = points.Count - 1 < 1 ? 0 : (loop ? points.Count : points.Count - 1);
                float standardized = (loop && max > 0) ? ((t %= max) + (t < 0 ? max : 0)) : Mathf.Clamp(t, 0, max);
                int rounded = Mathf.RoundToInt(standardized);
                int i1, i2;
                if (Mathf.Abs(standardized - rounded) < Mathf.Epsilon)
                    i1 = i2 = (rounded == points.Count) ? 0 : rounded;
                else
                {
                    i1 = Mathf.FloorToInt(standardized);
                    if (i1 >= points.Count)
                    {
                        standardized -= max;
                        i1 = 0;
                    }
                    i2 = Mathf.CeilToInt(standardized);
                    i2 = i2 >= points.Count ? 0 : i2;
                }
                retVal = i1 == i2 ? points[i1].position : BezierCurveUtility.Bezier3(points[i1].position,
                    points[i1].position + points[i1].tangent, points[i2].position
                    - points[i2].tangent, points[i2].position, standardized - i1);
            }
            return retVal;
        }
    }
}

using System;
using UnityEngine;

namespace SK.Framework
{
    [Serializable]
    public struct BezierCurvePoint
    {
        /// <summary>
        /// 坐标点
        /// </summary>
        public Vector3 position;

        /// <summary>
        /// 控制点 与坐标点形成切线
        /// </summary>
        public Vector3 tangent;
    }
}

SimpleBezierCurvePath

SimpleBezierCurvePath

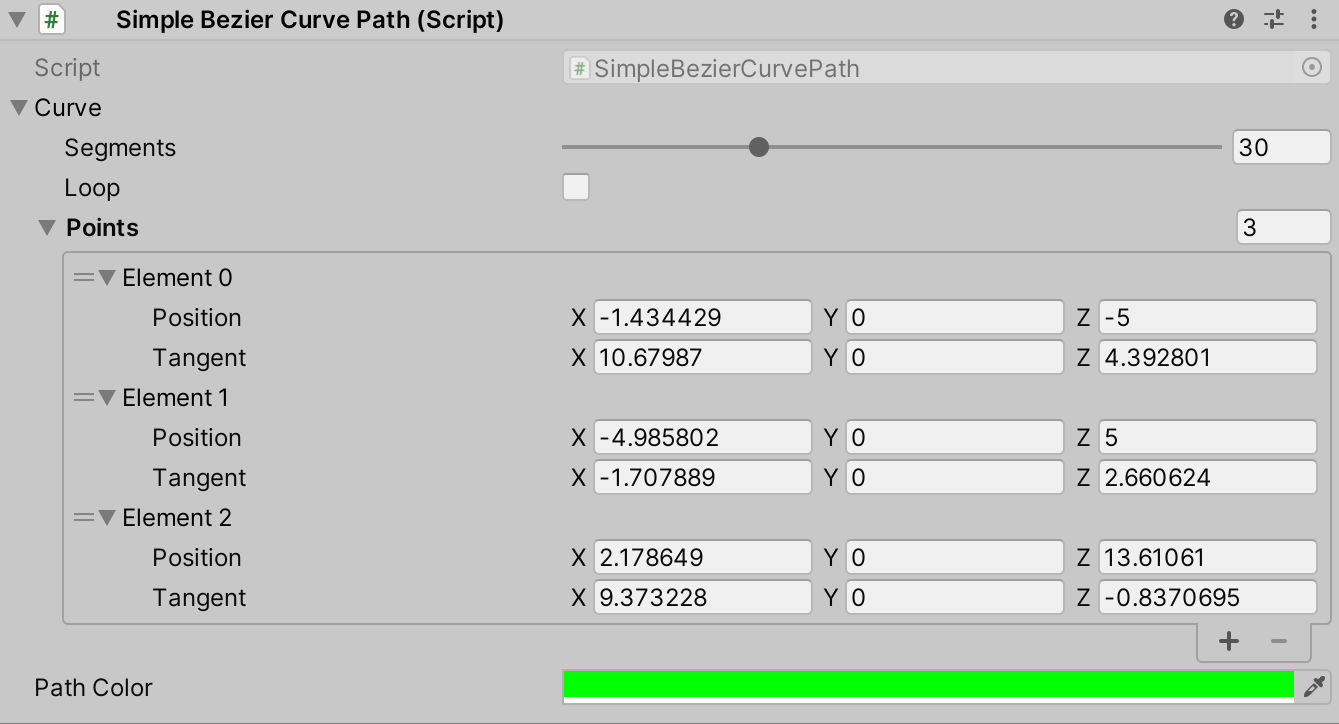
using UnityEngine;
using System.Collections.Generic;

#if UNITY_EDITOR
using UnityEditor;
#endif

namespace SK.Framework
{
    /// <summary>
    /// 贝塞尔曲线路径
    /// </summary>
    public class SimpleBezierCurvePath : MonoBehaviour
    {
        [SerializeField] private BezierCurve curve;

        public bool Loop { get { return curve.loop; } }

        public List<BezierCurvePoint> Points { get { return curve.points; } }

        /// <summary>
        /// 根据归一化位置值获取对应的贝塞尔曲线上的点
        /// </summary>
        /// <param name="t">归一化位置值 [0,1]</param>
        /// <returns></returns>
        public Vector3 EvaluatePosition(float t)
        {
            return curve.EvaluatePosition(t);
        }

#if UNITY_EDITOR
        /// <summary>
        /// 路径颜色(Gizmos)
        /// </summary>
        public Color pathColor = Color.green;

        private void OnDrawGizmos()
        {
            if (curve.points.Count == 0) return;
            //缓存颜色
            Color cacheColor = Gizmos.color;
            //路径绘制颜色
            Gizmos.color = pathColor;
            //步长
            float step = 1f / curve.segments;
            //缓存上个坐标点
            Vector3 lastPos = transform.TransformPoint(curve.EvaluatePosition(0f));
            float end = (curve.points.Count - 1 < 1 ? 0 : (curve.loop ? curve.points.Count : curve.points.Count - 1)) + step * .5f;
            for (float t = step; t <= end; t += step)
            {
                //计算位置
                Vector3 p = transform.TransformPoint(curve.EvaluatePosition(t));
                //绘制曲线
                Gizmos.DrawLine(lastPos, p);
                //记录
                lastPos = p;
            }
            //恢复颜色
            Gizmos.color = cacheColor;
        }
#endif
    }

#if UNITY_EDITOR
    [CustomEditor(typeof(SimpleBezierCurvePath))]
    public class SimpleBezierCurvePathEditor : Editor
    {
        private SimpleBezierCurvePath path;
        private const float sphereHandleCapSize = .2f;

        private void OnEnable()
        {
            path = target as SimpleBezierCurvePath;
        }

        private void OnSceneGUI()
        {
            //路径点集合为空
            if (path.Points == null || path.Points.Count == 0) return;
            //当前选中工具非移动工具
            if (Tools.current != Tool.Move) return;
            //颜色缓存
            Color cacheColor = Handles.color;
            Handles.color = Color.yellow;
            //遍历路径点集合
            for (int i = 0; i < path.Points.Count; i++)
            {
                DrawPositionHandle(i);
                DrawTangentHandle(i);

                BezierCurvePoint point = path.Points[i];
                //局部转全局坐标 路径点、控制点 
                Vector3 position = path.transform.TransformPoint(point.position);
                Vector3 controlPoint = path.transform.TransformPoint(point.tangent);
                //绘制切线
                Handles.DrawDottedLine(position, controlPoint + position, 1f);
            }
            //恢复颜色
            Handles.color = cacheColor;
        }

        //路径点操作柄绘制
        private void DrawPositionHandle(int index)
        {
            BezierCurvePoint point = path.Points[index];
            //局部转全局坐标
            Vector3 position = path.transform.TransformPoint(point.position);
            //操作柄的旋转类型
            Quaternion rotation = Tools.pivotRotation == PivotRotation.Local
                ? path.transform.rotation : Quaternion.identity;
            //操作柄的大小
            float size = HandleUtility.GetHandleSize(position) * sphereHandleCapSize;
            //在该路径点绘制一个球形
            Handles.color = Color.white;
            Handles.SphereHandleCap(0, position, rotation, size, EventType.Repaint);
            Handles.Label(position, string.Format("Point{0}", index));
            //检测变更
            EditorGUI.BeginChangeCheck();
            //坐标操作柄
            position = Handles.PositionHandle(position, rotation);
            //变更检测结束 如果发生变更 更新路径点
            if (EditorGUI.EndChangeCheck())
            {
                //记录操作
                Undo.RecordObject(path, "Position Changed");
                //全局转局部坐标
                point.position = path.transform.InverseTransformPoint(position);
                //更新路径点
                path.Points[index] = point;
            }
        }

        //控制点操作柄绘制
        private void DrawTangentHandle(int index)
        {
            BezierCurvePoint point = path.Points[index];
            //局部转全局坐标
            Vector3 cp = path.transform.TransformPoint(point.position + point.tangent);
            //操作柄的旋转类型
            Quaternion rotation = Tools.pivotRotation == PivotRotation.Local
                ? path.transform.rotation : Quaternion.identity;
            //操作柄的大小
            float size = HandleUtility.GetHandleSize(cp) * sphereHandleCapSize;
            //在该控制点绘制一个球形
            Handles.color = Color.yellow;
            Handles.SphereHandleCap(0, cp, rotation, size, EventType.Repaint);
            //检测变更
            EditorGUI.BeginChangeCheck();
            //坐标操作柄
            cp = Handles.PositionHandle(cp, rotation);
            //变更检测结束 如果发生变更 更新路径点
            if (EditorGUI.EndChangeCheck())
            {
                //记录操作
                Undo.RecordObject(path, "Control Point Changed");
                //全局转局部坐标
                point.tangent = path.transform.InverseTransformPoint(cp) - point.position;
                //更新路径点
                path.Points[index] = point;
            }
        }
    }
#endif
}

SimpleBezierCurvePathAlonger

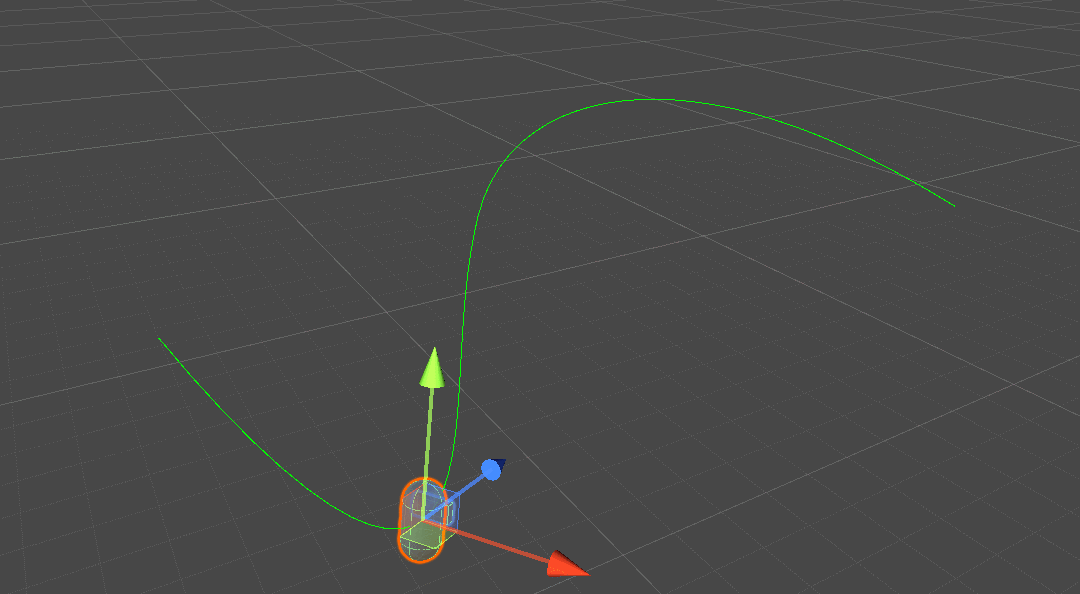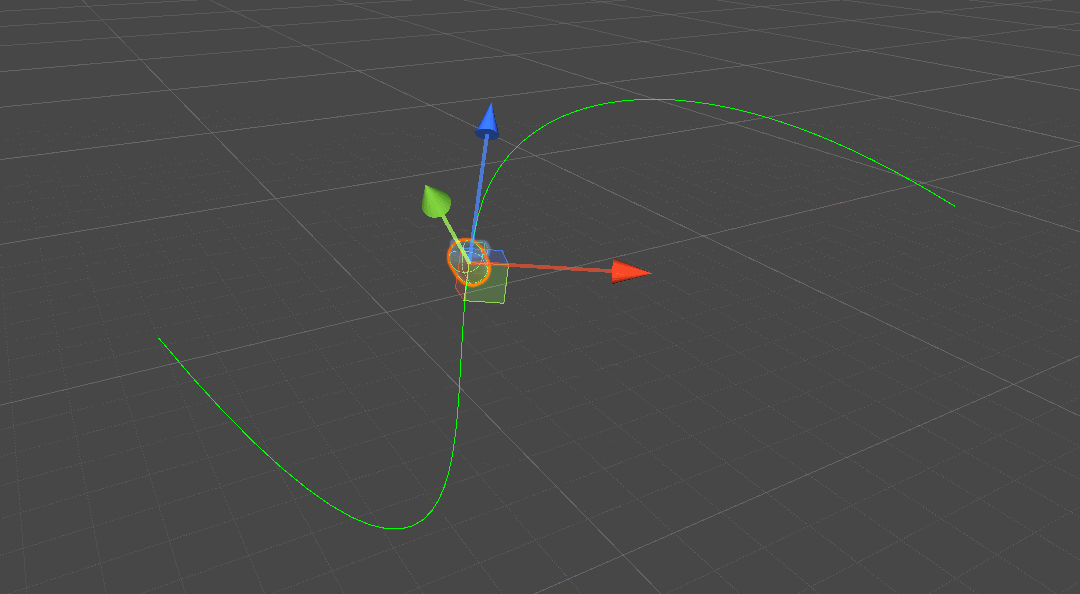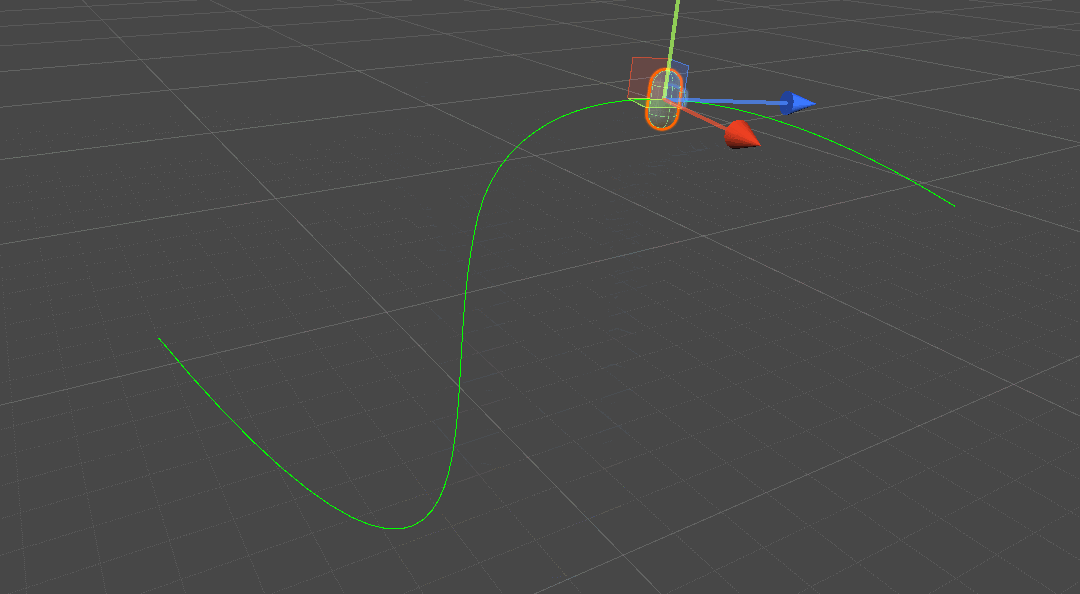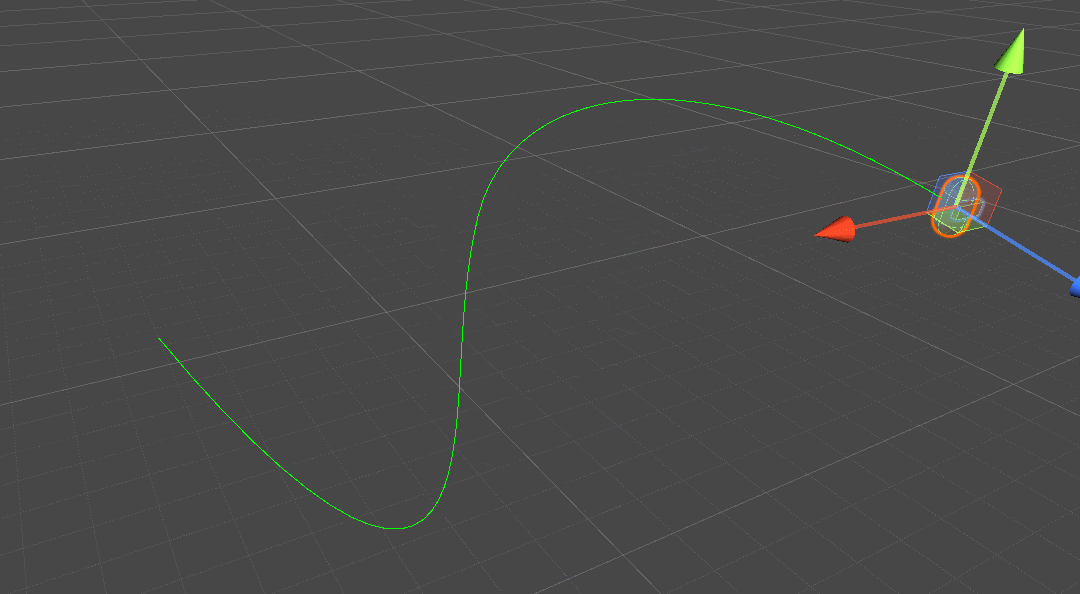
SimpleBezierCurvePathAlonger

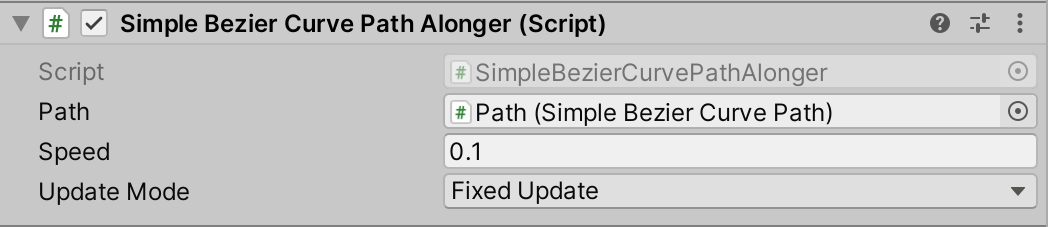
  • path：贝塞尔曲线路径；
  • speed：移动速度；
  • update Mode：更新方式（FixedUpdate、Update、LateUpdate）
using UnityEngine;

namespace SK.Framework
{
    public class SimpleBezierCurvePathAlonger : MonoBehaviour
    {
        public enum UpdateMode
        {
            FixedUpdate,
            Update,
            LateUpdate,
        }

        [SerializeField] private SimpleBezierCurvePath path;

        [SerializeField] private float speed = .1f;

        [SerializeField] private UpdateMode updateMode = UpdateMode.Update;

        private float normalized = 0f;

        private Vector3 lastPosition;

        private void FixedUpdate()
        {
            if (updateMode == UpdateMode.FixedUpdate && path != null)
                MoveAlongPath();
        }

        private void Update()
        {
            if (updateMode == UpdateMode.Update && path != null)
                MoveAlongPath();
        }

        private void LateUpdate()
        {
            if (updateMode == UpdateMode.LateUpdate && path != null)
                MoveAlongPath();
        }

        private void MoveAlongPath()
        {
            float t = normalized + speed * Time.deltaTime;
            float max = path.Points.Count - 1 < 1 ? 0 : (path.Loop ? path.Points.Count : path.Points.Count - 1);
            normalized = (path.Loop && max > 0) ? ((t %= max) + (t < 0 ? max : 0)) : Mathf.Clamp(t, 0, max);
            transform.position = path.EvaluatePosition(normalized);
            Vector3 forward = transform.position - lastPosition;
            transform.forward = forward != Vector3.zero ? forward : transform.forward;
            lastPosition = transform.position;
        }
    }
}

沿贝塞尔曲线路径移动

源码已上传至SKFramework框架Package Manager中：

SKFramework PackageManager

参考链接：

  1. 贝塞尔曲线 - 百度百科
  2. Unity Cinemachine Path
  3. Unity 贝塞尔曲线（Beizer curve）的原理与运用

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/415364.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

人工智能概述

人工智能概述

一、人工智能发展必备三要素 算法 数据 算力 CPU、GPU、TPU 计算力之CPU、GPU对比&#xff1a; CPU主要适合I\O密集型任务GPU主要适合计算密集型任务 什么样的程序适合在GPU上运行&#xff1f; 计算密集型的程序 所谓计算密集型(Compute-intensive)的程序&#xff0c;就是…
阅读更多...
【K8S系列】深入解析无状态服务

【K8S系列】深入解析无状态服务

目录 序言 1. 无服务介绍 1.1 优点 1.2 使用场景 1.3 资源类型 1.4 总结 2 使用介绍 2.1 Deployment 使用场景&#xff1a; 2.2 ReplicaSet 使用场景 2.3 pod Pod 资源定义示例 2.4 service 创建一个Deployment&#xff1a; 创建一个Service&#xff1a; 总结…
阅读更多...
前置知识——Linux网络虚拟化

前置知识——Linux网络虚拟化

Linux网络虚拟化 信息是如何通过网络传输被另一个程序接收到的&#xff1f; 我们讨论的虚拟化网络是狭义的&#xff0c;它指容器间网络。 好了&#xff0c;下面我们就从 Linux 下网络通信的协议栈模型&#xff0c;以及程序如何干涉在协议栈中流动的信息来开始了解吧。 Linux…
阅读更多...
基于飞桨实现的特定领域知识图谱融合方案：ERNIE-Gram文本匹配算法

基于飞桨实现的特定领域知识图谱融合方案：ERNIE-Gram文本匹配算法

文本匹配任务在自然语言处理领域中是非常重要的基础任务&#xff0c;一般用于研究两段文本之间的关系。文本匹配任务存在很多应用场景&#xff0c;如信息检索、问答系统、智能对话、文本鉴别、智能推荐、文本数据去重、文本相似度计算、自然语言推理、问答系统、信息检索等&…
阅读更多...
【MySQL】了解MySQL的Explain，读这一篇够了(￣∇￣)/

【MySQL】了解MySQL的Explain，读这一篇够了(￣∇￣)/

目录 ID select_type 查询类型 table 表名 type 关联类型/访问类型 possible_keys MySQL觉得可能要用到的索引 key 实际用到的索引 key_len 用到的索引的长度&#xff08;比如可用于判断使用了联合索引中的哪几个&#xff09; ref 表查找值所用的列&#xff08;表名.字…
阅读更多...
Transformer在计算机视觉中的应用-VIT、TNT模型

Transformer在计算机视觉中的应用-VIT、TNT模型

上期介绍了Transformer的结构、特点和作用等方面的知识&#xff0c;回头看下来这一模型并不难&#xff0c;依旧是传统机器翻译模型中常见的seq2seq网络&#xff0c;里面加入了注意力机制&#xff0c;QKV矩阵的运算使得计算并行。 当然&#xff0c;最大的重点不是矩阵运算&…
阅读更多...
行人车辆检测与计数系统（Python+YOLOv5深度学习模型+清新界面）

行人车辆检测与计数系统（Python+YOLOv5深度学习模型+清新界面）

摘要&#xff1a;行人车辆检测与计数系统用于交通路口行人及车辆检测计数&#xff0c;道路人流量、车流量智能监测&#xff0c;方便记录、显示、查看和保存检测结果。本文详细介绍行人车辆检测&#xff0c;在介绍算法原理的同时&#xff0c;给出Python的实现代码、PyQt的UI界面…
阅读更多...
【并发编程Python】一文详解Python并发编程，协程、线程、进程

【并发编程Python】一文详解Python并发编程，协程、线程、进程

并发编程简介和一些前缀知识 并发编程是使得程序大幅度提速的。在并发编程中&#xff0c;程序可以同一时间执行多个任务&#xff0c;这有助于提高程序的吞吐量和响应时间。并发编程设计的主要概念包括线程、锁、同步、信号量、进程间通信等。 前缀知识&#xff1a; IO&#x…
阅读更多...
Linux中shell内外命令讲解（上）

Linux中shell内外命令讲解（上）

♥️作者：小刘在C站 ♥️个人主页：小刘主页 ♥️每天分享云计算网络运维课堂笔记，努力不一定有收获，但一定会有收获加油！一起努力，共赴美好人生！ ♥️夕阳下，是最美的绽放，树高千尺，落叶归根人生不易，人间真情 前言 本章Linuxshell讲解，感谢观看，干货满满。 目录…
阅读更多...
在windows内使用virtualbox搭建安卓x86，以及所遇到的问题解决--2.virtualbox上安卓x86的配置

在windows内使用virtualbox搭建安卓x86，以及所遇到的问题解决--2.virtualbox上安卓x86的配置

目录: 简要说明&#xff1a; 1.配置vesa驱动&#xff1a; 2.启用网络连接并配置adb&#xff1a; 3.增强性能的方法&#xff1a; 简要说明&#xff1a; 先进行说明一点个人直接通过vbox VMware这些软件&#xff0c;并不能超越专业的安卓模拟器&#xff0c;大部分模拟器实际…
阅读更多...
使用Pytorch实现对比学习SimCLR 进行自监督预训练

使用Pytorch实现对比学习SimCLR 进行自监督预训练

SimCLR&#xff08;Simple Framework for Contrastive Learning of Representations&#xff09;是一种学习图像表示的自监督技术。 与传统的监督学习方法不同&#xff0c;SimCLR 不依赖标记数据来学习有用的表示。 它利用对比学习框架来学习一组有用的特征&#xff0c;这些特征…
阅读更多...
【创作赢红包】Java Web 实战 18 - 计算机网络之网络层协议 and 数据链路层协议

【创作赢红包】Java Web 实战 18 - 计算机网络之网络层协议 and 数据链路层协议

文章目录网络层协议1. IP 协议1.1 报头结构1.2 IP 协议的地址管理动态分配 IP 地址 (DHCP)IP 地址转换 (NAT)IPv61.3 IP 地址的组成2. 路由选择数据链路层1. 以太网协议2. 以太网帧格式2.1 mac 地址2.2 两个特殊的以太网数据帧DNS 域名解析系统六 . 经典面试题 : 从浏览器中输入…
阅读更多...
微信小程序 | 基于ChatGPT实现模拟面试小程序

微信小程序 | 基于ChatGPT实现模拟面试小程序

Pre&#xff1a;效果预览 ① 选择职位进行面试 ② 根据岗位职责进行回答 一、需求背景 这两年IT互联网行业进入寒冬期&#xff0c;降本增效、互联网毕业、暂停校招岗位的招聘&#xff0c;各类裁员、缩招的情况层出不穷&#xff01;对于这个市场来说&#xff0c;在经历了互联网…
阅读更多...
小白学Pytorch系列--Torch API (7)

小白学Pytorch系列--Torch API (7)

小白学Pytorch系列–Torch API (7) Comparison Ops allclose 此函数检查输入和其他是否满足条件&#xff1a; >>> torch.allclose(torch.tensor([10000., 1e-07]), torch.tensor([10000.1, 1e-08])) False >>> torch.allclose(torch.tensor([10000., 1e-…
阅读更多...
MATLAB | 如何自然好看的从图片中提取颜色并制作色卡

MATLAB | 如何自然好看的从图片中提取颜色并制作色卡

在这里研究了一下各种排序算法&#xff0c;写一篇如何由图片一键生成颜色条的方法。 1 关于大量颜色排序 假设有大量颜色怎么对其进行排序呢&#xff0c;首先想到的最简单方法就是将其按照RGB值的大小进行排序&#xff0c;为了方便展示颜色条&#xff0c;这里编写了一个颜色条…
阅读更多...
【Pytorch】 理解张量Tensor

【Pytorch】 理解张量Tensor

本文参加新星计划人工智能(Pytorch)赛道&#xff1a;https://bbs.csdn.net/topics/613989052 这是目录张量Tensor是什么&#xff1f;张量的创建为什么要用张量Tensor呢&#xff1f;总结张量Tensor是什么&#xff1f; 在深度学习中&#xff0c;我们经常会遇到一个概念&#xff…
阅读更多...
初探Redis整体架构

初探Redis整体架构

文章目录1、Redis为什么选择单线程2、逐步加入多线程3、Redis采用IO多路复用---epoll和Reactor架构4、Redis6/7默认是否开启了多线程&#xff1f;1、Redis为什么选择单线程 这种问法其实并不严谨&#xff0c;为啥这么说呢? Redis几个里程碑式的重要版本 理清一个事实&#…
阅读更多...
一文带你安装opencv和常用库（保姆级教程少走80%的弯路）

一文带你安装opencv和常用库（保姆级教程少走80%的弯路）

0.导语 离上一个opencv安装保姆级教程发布已经过去了快一年了&#xff0c;这一年来我收到了来自很多C友的鼓励。打算学opencv的各位朋友都会在安装opencv和各种库过程中浪费掉60%的时间和精力&#xff1b;博主在这一年来尝试各种各样的安装方法&#xff0c;全网搜集各种资料总…
阅读更多...
[ 云计算 | Azure ] Chapter 05 | 核心体系结构之管理组、订阅、资源和资源组以及层次关系

[ 云计算 | Azure ] Chapter 05 | 核心体系结构之管理组、订阅、资源和资源组以及层次关系

本文主要对如下内容进行讲解&#xff1a;Azure云计算的核心体系结构组件中的&#xff1a;资源、订阅和资源组&#xff0c;以及了解 Azure 资源管理器 (ARM) 如何部署资源。 本系列已经更新文章列表&#xff1a; [ 云计算 | Azure ] Chapter 03 | 描述云计算运营中的 CapEx 与…
阅读更多...
元宇宙与网络安全

元宇宙与网络安全

元宇宙是一种虚拟现实空间&#xff0c;用户可以在计算机生成的环境中进行互动。元宇宙的应用范围很广&#xff0c;比如房地产&#xff0c;医疗&#xff0c;教育&#xff0c;军事&#xff0c;游戏等等。它提供了更具沉浸感的体验&#xff0c;更好地现实生活整合&#xff0c;以及…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023