标准化归一化方法

news2025/1/18 6:24:31

一、经典机器学习的归一化算法

分别是0-1标准化（Max-Min Normalization）和Z-Score标准化。

1.1 0-1标准化方法

每一列中的元素减去当前列的最小值，再除以该列的极差。
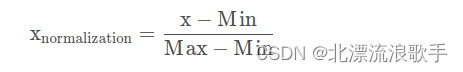
在这里插入图片描述

不过在深度学习领域，我们更希望输入模型的数据是Zero-Centered Data，此时Z-Score标准化会更加合适。

1.2 Z-Score标准化

Z-Score标准化并不会将数据放缩在0-1之间，而是均匀地分布在0的两侧。类似这种数据也被称为Zero-Centered Data，在深度学习领域有重要应用。当然我们可以将上述过程封装为一个函数：
同样是逐列进行操作，每一条数据都减去当前列的均值再除以当前列的标准差。很明显，通过这种方法处理之后的数据是典型的Zero-Centered Data，
并且如果原数据服从正态分布，通过Z-Score处理之后将服从标准正态分布。
Z-Score标准化计算公式如下：
在这里插入图片描述
其中μ 代表均值，σ 代表标准差。当然，我们也可通过如下方式对张量进行Z-Score标准化处理。

def z_score(X):
    """
    Z-Score标准化函数
    """
    return (X - X.mean(axis=0)) / X.std(axis=0)

a
#array([[ 0,  1],
#       [ 2,  3],
#       [ 4,  5],
#       [ 6,  7],
#       [ 8,  9],
#       [10, 11]])
# 每列均值
a.mean(0)
#array([5., 6.])
# 每列标准差
a.std(0)
#array([3.41565026, 3.41565026])
(a - a.mean(0))
#array([[-5., -5.],
#       [-3., -3.],
#       [-1., -1.],
#       [ 1.,  1.],
#       [ 3.,  3.],
#       [ 5.,  5.]])
# Z-Score标准化
(a - a.mean(0)) / a.std(0)
#array([[-1.46385011, -1.46385011],
#       [-0.87831007, -0.87831007],
#       [-0.29277002, -0.29277002],
#       [ 0.29277002,  0.29277002],
#       [ 0.87831007,  0.87831007],
#       [ 1.46385011,  1.46385011]])

def Z_ScoreNormalization(data):
    stdDf = data.std(0)
    meanDf = data.mean(0)
    normSet = (data - meanDf) / stdDf
    return normSet

二、标准化、归一化的原因、用途

统计建模中，如回归模型，自变量的量纲不一致导致了回归系数无法直接解读或者错误解读；为了消除数据特征之间的量纲影响，我们需要对特征进行归一化处理，使得不同指标之间具有可比性；
机器学习任务和统计学任务中有很多地方要用到“距离”的计算，比如PCA，比如KNN，比如kmeans等等，假使算欧式距离，不同维度量纲不同可能会导致距离的计算依赖于量纲较大的那些特征而得到不合理的结果；
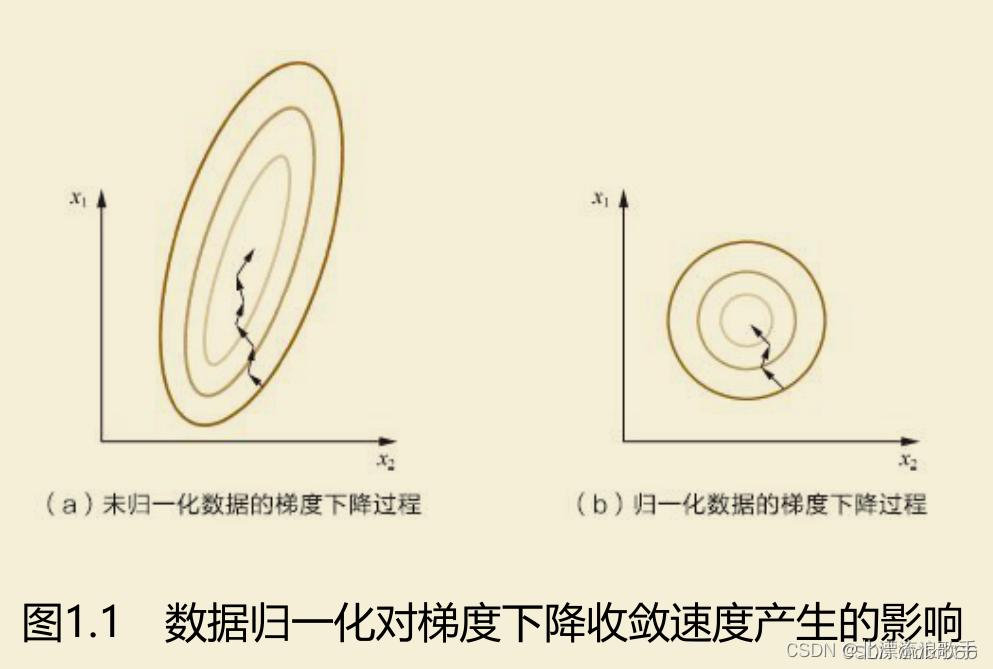
参数估计时使用梯度下降，在使用梯度下降的方法求解最优化问题时，归一化/标准化后可以加快梯度下降的求解速度，即提升模型的收敛速度。
例子
归一化之后等高线变得不再崎岖，x1和x2的更新速度变得更为一致，容易更快地通过梯度下降找到最优解。迭代次数变少，减小梯度下降算法的过程，从而加速模型的生成。
在这里插入图片描述

哪些模型必须归一化

1、在分类、聚类算法中，需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候，标准化(Z-score standardization)表现更好。
2、在不涉及距离度量、协方差计算、数据不符合正太分布的时候，可以使用归一化方法。比如图像处理中，将RGB图像转换为灰度图像后将其值限定在[0 255]的范围。
实际应用中，通过梯度下降法求解模型的通常需要归一化，包括线性回归、逻辑回归、支持向量机、神经网络等。