14届蓝桥杯Python总结

在比赛的时候大家头脑注意力都高度集中，比较紧绷，我是不喜欢太紧绷的神经的，这时候电脑就夸得一下关机重启了，我当时真的想说关的好，休息一会（哈哈哈）

重启后我就继续做题，虽然出了点小插曲，但还好。

以下是我在比赛时做出的一部分题目，总结一下，今年蓝桥杯是两道填空题加8道程序题，感觉难度应该是提高了。

试题 A: 2023（5分）

【问题描述】

请求出在 12345678 至 98765432 中，有多少个数中完全不包含 2023 。完全不包含 2023 是指无论将这个数的哪些数位移除都不能得到 2023 。例如 20322175，33220022 都完全不包含 2023，而 20230415，20193213 则含有 2023 (后者取第 1, 2, 6, 8 个数位) 。

【答案提交】

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

代码及思路：

一定要申清题目，我当时做的时候头脑有点不清醒，想着不包含，写着写着就变成包含了。。。，5分就这样没了

暴力循环求解

ans = 0

def find(x):
    tmp = "2023"
    a = str(x)
    j = 0
    for i in a:  # 对数字进行遍历
        if i == tmp[j]:  # 从左到右逐个遍历是否依次会出现2023四个数字
            j += 1
        if j == 4:   # 说明完全包含2023
            return True
    return False


for i in range(12345678,98765433):
    if not find(i):  # 注意这里要的是完全不包含2023，
        ans += 1        # 要取反加not，我这里没仔细看，结果就是反向答案
print(ans)

# print(98765433 -12345678 - 460725) # 用反向答案求答案。。。

# 反向答案 460725
# 答案 85959030

试题 B: 硬币兑换（5分）

代码及思路：

这道题在比赛时，我首先看了一眼没有思路就跳过去了，再后来要交卷了，想起来这个填空题还没有写，匆忙之下就想着2023有2023个，最后加一起的时候应该也是最多的，那么谁加谁等于2023，我很直接的想到了1011+1012，有1011个，然后加上2023个交卷了。事后在看这个突然发现答案与我擦肩而过，既然1011+1012=2023，那么1010+1013 = 1009+1014 = ... = 1 + 2022,都满足等于2023，且个数依次就是从1加到1011个，最后再加上新的2023就是答案了？？？

不，这只是比较直接的想法，在已有的硬币中有1~2023，生成的硬币在这里面的话和为2023最后是最多的，但可以生成硬币值大于2023的新的硬币，这样就是另一种情况了。

根据两个硬币加和为新硬币值，可以发现最后加的一次为 (新硬币值-1) / 2，以2023为例，从1+2+..+1011, 最后加到了1011结束，类推之后，我们暂且把最后加和的新硬币值设为NewSum，加和的最后一个硬币值设为End，加和的起始硬币为Start，则有NewSum = End * 2 + 1，又因为新硬币值为Start+2023，有NewSum = Start + 2023，又因为最后的种数是以Start为首项，1为公差的等差数列的和，项数共有End - Start + 1项。

可以得到和为NewSum的种数为 Sn = (End - Start + 1) * (Start + End) / 2

结合NewSum = End * 2 + 1，NewSum = Start + 2023。

我们可以得到关于End的一个方程， $Sn = -\frac{1}{2} * (3End^{2} - 8091End + 2022*2023)$

是一个开口向下的二次函数，化简内部关键部分得， $Sn = -\frac{3}{2} * (End - 1348.5)^{2} + \partial$

可知当End为 1348.5 时种数取得最大值，因为只能取整数，则End取1348和1349都行。

代入方程得Sn = 682425

ans = 2023  # 现有的2023个
for i in range(1,1012):
    ans += i  # 合成的2023的个数
print(ans)  # 513589

ans = 0
# 当我们化简完式子就知道End取什么值了，不化简用代码来枚举也是同样的
for End in range(1012,2023):  # 由公式知，end是变量，end使Sn最优
    NewSum = End * 2 + 1    # 大于2023的新硬币值
    Start = NewSum - 2023   # 起始的第一个数
    Sn = (End - Start + 1) * (Start + End) // 2  # 数列求和公式
    if Sn > ans:   
        ans = Sn 
    else: 
        print(ans)  # 682425
        break

试题 C: 松散子序列（10分）

代码及思路：

正确理解：根据pi-p(i-1)>=2，这里pi 是原字符串的下标，即在子串中两个相邻的字符在原字符串中的下标至少要相邻2.要获得子串的最大值，并且满足条件，可以使用递推，即子序列中后一位的最大值由前一位最大值加上本身的值得到。使用动态规划进行动态递推。创建dp数组，令 dp[i] 表示以第 i 个字符结尾的松散子序列中的最大价值，定义一个指针K来表示满足 pi − pk ≥ 2 的最大的位置，通过转移方程dp[i] = dp[k] + val[s[i]]更新最大值。

def getmax_value(s):
    n = len(s)
    # res = ""
    dp = [0] * n   # 创建dp数组，令 dp[i] 表示以第 i 个字符结尾的松散子序列中的最大价值
    val = {chr(i+97): i+1 for i in range(26)}  # 创建一个字母:值的字典,便于获取字母的值
    # print(val)
    k = -1      # 定义一个指针K来表示满足 pi − pk ≥ 2 的最大的位置，通过转移方程dp[i] = dp[k] + val[s[i]]更新最大值
    for i in range(n):
        if i == 0:
            dp[i] = val[s[i]]   # 把第一个字母的价值赋值
        elif i == 1:
            dp[i] = max(val[s[i]], dp[i-1])  # 保存最大值
        else:
            while k < i-2 or (k >= 0 and s[k+1:k+3] != s[i-1:i+1]):  # k == i - 2跳出循环
                k += 1   # k来记录满足pi-pk >= 2的最大位置,（逐个递增）
            # res += s[k]
            dp[i] = dp[k] + val[s[i]]   # 递推，当前位置值最大值为前一个满足距离条件的最大值+现在的值
            dp[i] = max(dp[i], dp[i-1])  # 现在的位置更新最大值，保证k位置最大值是k其前面的最大值，
    # print(res)
    return dp[-1]  # 最后为整体最大值

s = input()  # azaazaz
ans = getmax_value(s)
print(ans)

错误理解：t是原序列的子序列，就是其中任意一部分。然后看定义就是说松散子序列满足当前字母的价值减去前一个字母的价值要大于等于2.，然后就暴力循环判断，测试用例只有一个，看着答案对了，就没多想。。。

s = input()   #"azaazaz"
ans = ""
res = 0
length = len(s)
for i in range(1,length):
    if ord(s[i]) - ord(s[i-1]) >= 2:  # 满足条件，说明是子序列中的一个
        ans += s[i]
        res += ord(s[i]) - 96  # 价值从1开始

# print(ans)   # zzz
print(res)   # 78

试题 D: 管道（10分）

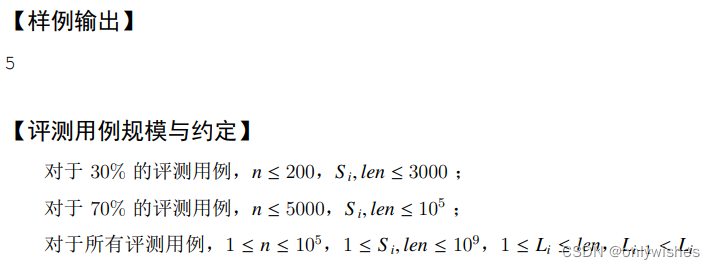
代码及思路：

首先吐槽一下，为什么测试样例只给一个啊，我写出来，为了测试一下样例，把代码中的范围缩小了下，结果就是缩小了没有改回去，真正测试肯定不通过的（还是怪自己粗心，白忙活了。。。）

这道题要求管道中每一段都检测到有水流，然后求这个条件的最早时间，在由管道每一段它根据时间不同，它周围的某一区间管道也会检测到，根据这种与区间相关的性质，我们可以想到用差分数组和前缀和来进行操作区间。如下图，构造一个区间数组，初始状态为0 ，然后对每一次时间的值，根据给的区间公式 Li-（Ti-Si）~ Li+（Ti-Si）进行求出区间左边和右边，这就可以用到差分数组，在当前t时间时对每个阀门进行求区间，然后对区间加一，当最后dp数组中从起始位置1到管道最右边都为1时，说明每段都检测到了水流，输出时间t，退出循环。

这里时间T需要我们自己寻找，那么就有遍历查找和二分查找两种方法数据量太大，暴力是过不完的。

下面是暴力解的思路：

在此基础上加上二分可以降低遍历时间 t 的时间复杂度O(n)为O(logn）

n,len = map(int,input().split())
L,S = [],[]
for i in range(n):
    a,b = map(int,input().split())
    L.append(a)
    S.append(b)
minS = min(S)  # 直接让t从最小的Si开始，就能开始检测了


for t in range(minS,100000000):  # 就是这里t的范围一定要大，。。
    dp = [0] * (len+2)  # 构造dp数组记录状态，我们定义数组管道长度区间中全为1时，t即为答案
    # 构建差分数组
    for i in range(n, 0, -1):
        dp[i] -= dp[i - 1]
    for i in range(n):  # 求一个阀门的左右区间
        if t >= S[i]:
            a = L[i] - (t-S[i])
            b = L[i] + (t-S[i])

            if a < 0:   # 最左边不能为负数
                a = 0
            if b > len:  # 最右边为管道长度
                b = len
            # print(a,b)
            # 转换加减(区间加减-->端点加减)
            dp[a] += 1
            dp[b+1] -= 1
    # 前缀相加(前缀和公式)
    for i in range(1,len+2):
        dp[i] += dp[i-1]
    # print(dp)  # 查看dp数组
    if sum(dp[1:len+1]) == len:  # 区间全为1说明完成
        print(t)
        break

# 输入
3 10
1 1
6 5
10 2

# 查看dp数组
[0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0]
[1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0]
[1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0]
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0]

# ans
5

下面是加上二分进行优化后的代码：

我们就是要找一个时间 t ,满足 t 时刻刚好覆盖区间，用二分查找这样的时间 T 会比遍历快很多。

"""
3 10
1 1
6 5
10 2
"""

n,len = map(int,input().split())
L,S = [],[]
for i in range(n):
    a,b = map(int,input().split())
    L.append(a)
    S.append(b)


def checkT(t):  # 返回当前时间T的区间状态和
    dp = [0] * (len+2)  # 构造dp数组记录状态，我们定义数组管道长度区间中全为1时，t即为答案
    # 构建差分数组
    for i in range(n, 0, -1):
        dp[i] -= dp[i - 1]
    for i in range(n):  # 求一个阀门的左右区间
        if t >= S[i]:
            a = L[i] - (t-S[i])
            b = L[i] + (t-S[i])

            if a < 0:   # 最左边不能为负数
                a = 0
            if b > len:  # 最右边为管道长度
                b = len
            # print(a,b)
            # 转换加减(区间加减-->端点加减)
            dp[a] += 1
            dp[b+1] -= 1
    # 前缀相加(前缀和公式)
    for i in range(1,len+2):
        dp[i] += dp[i-1]
    # print(dp)  # 查看dp数组
    return sum(dp[1:len+1])  # 返回该时间的区间和

l,r = 1, 100000000
while l < r:
    mid = (l+r) // 2
    if checkT(mid) < len:  # 时间不够，没覆盖完
        l = mid + 1
    elif checkT(mid) > len:  # 时间太大，不是刚好的时候
        r = mid
    else:       # 此时时间 t 刚好完全覆盖区间范围
        print(mid)
        break

试题 E: 保险箱（15）

代码及思路：

这道题就是暴力模拟了，从最后一位数字进行比较，然后判断经过加还是减最小步骤相等，然后判断有进位么，有借位么，有的话更新数字，然后继续比较，直到两数相等，累记步骤和。

n = int(input())  # 位数
x = list(map(int,input()))  # 起始
y = list(map(int,input()))  # 目标

ans = 0

def getMinPro(a,b):  # 获得当前数字变为目标数字的最小步数
    """
    :param a: 数字a变为b
    :param b:
    :return: 返回两个数，一个是a->b的步数，一个是（1,0，-1）分别表示进位加1，不变，进位减一
    """
    if a < b:   # 如果当前数字比目标数字小
        if 10-b+a > b-a:  # 一种是当前数字加x个数比减去y个数小
            return b-a,0
        else:  # 一种是当前数字加x个数比减去x个数多，这种要减
            return 10-b+a,-1   # 返回减去某个数，因为a本就小于b，减，肯定要借位，即进位减1
    elif a > b:  # 如果当前数字比目标数字大
        if 10-a+b < a-b:  # 一种是当前数字加x个数比减去y个数小
            return 10-a+b,1  # 返回加上多少个数，因为a本来就大于b ,肯定进位加1
        else:   # 一种是当前数字加x个数比减去y个数小
            return a-b,0
    else:
        return 0,0   # a,b 相等则返回0,0

def addT(x,i):  # 向高位进行进位，逢九加1=10进位
    while i >=0:
        x[i-1] += 1
        if x[i-1] == 10:
            x[i-1] = 0
            i -= 1
        else:
            break
def subT(x,i):  # 向高位借位，即高位减1，逢0减1=-1，变9继续借位
    while i >0:
        x[i-1] -= 1
        if x[i-1] == -1:
            x[i-1] = 9
            i -= 1
        else:
            break

i = n-1  # 在数组中，0是第一位，n-1为最后一位
while i>=0:   # 从最后一位开始比较两数
    buzhou,flag = getMinPro(x[i],y[i])
    # print(buzhou,flag)  # 每位的步骤及进位情况
    if flag == 1:  # 进位加，就更新数组数字
        addT(x,i)
    elif flag == -1:  # 借位减，更新数组数字
        subT(x,i)
    ans += buzhou  # 步骤加和
    i -= 1  # 当前数位比较完成，向高位推进，
print(ans)

# 输入
5
12349
54321

# 每位的步骤及进位情况
2 1
3 0
0 0
2 0
4 0

# 答案
11

试题 J: 混乱的数组（25）

代码及思路：

前5题写完时间已经不多了，看到最后一题题干这么少，测试规模x<=10!!! 这不就意味着我写10个if判断就能拿30%的分了o(*￣▽￣*)o ，于是我就真的写了10个判断。刚开始写的过程中，发现如果数字不重复的话好像只有3是321,6是4321,10是54321，而其他的数字没办法写，所以肯定会有重复数字，这样就好办了，就枚举数字找低位的数字小于高位的数字的总个数为要求的种数就行。

然而这种只能保证拿30%的分数，对于后面的要如何做才能拿到一些呢，观察一下3= 3*2 / 2

6 = 4*3 / 2 ,10 = 5*4 / 2, 发现满足一个规律，就是他们后面都是倒序遍历到1,321,4321,54321

那么以6为例可以把4看为n,3看为n-1 ，就满足n*(n-1) / 2 = x, x是我们输入的是已知的，那么把x当做常数，求n就行，最后输出就是从n到1的遍历输出。解方程得 n = (1+sqrt(1+8x)) / 2

那么对于3,6,10,15,21,28....这种特殊的数也可以输出正确答案了，他们的输出为321,4321,54321,654321,7654321,87654321....用空格隔开就好。

import math
x = int(input())
if x == 1:
    print(2)
    print(2,1,sep=" ")
elif x==2:
    print(3)
    print(2,1,1,sep=" ")
elif x==3:
    print(3)
    print(3,2,1,sep=" ")
elif x==4:
    print(4)
    print(2,2,1,1,sep=" ")
elif x==5:
    print(4)
    print(3,2,1,1,sep=" ")
elif x==6:
    print(4)
    print(4,3,2,1,sep=" ")
elif x==7:
    print(5)
    print(3,2,1,1,1,sep=" ")
elif x==8:
    print(5)
    print(3,3,2,1,1,sep=" ")
elif x==9:
    print(5)
    print(4,3,2,1,1,sep=" ")
elif x==10:
    print(5)
    print(5,4,3,2,1,sep=" ")
elif x > 10:
    n = (1 + math.sqrt(1 + 8 * x)) / 2
    print(int(n))
    for i in range(int(n), 0, -1):
        print(i, end=" ")

# 输入
28
# 输出
8
8 7 6 5 4 3 2 1

写到这里就结束了，第6,7,8,9道题当时没时间看了。最让我痛心的还是第1道题和第四道管道这两题，尤其是管道这题，写完了，测试一下数据，把t的右区间改成了7，没改回来，这我自己都不明白我这什么操作{{{(>_<)}}}，以后注意，这种感觉太难受了→_→，以上解法为我个人的解法，可能存在问题，欢迎大家指正。