1.简介
为了了解模型的泛化能力,我们需要用某个指标来衡量,这就是性能度量的意义。常用的评估指标有:混淆矩阵(Confuse Matrix)、准确率(Accuracy)、精准率(Precision)和召回率(Recall)、F1-Score、ROC曲线(Receiver Operating Characteristic Curve)、AUC(Area Under the Curve)、P-R曲线 等等。
2.混淆矩阵
针对一个二分类问题,将实例分成正类(positive)和负类(negative)两种。
把预测情况与实际情况的所有结果两两混合,结果就会出现以下4种情况,就组成了混淆矩阵,其实也可以是多分类的,这里以二分类举例子。

- 真正例(True Positive,TP):预测为正样本,真实也为正样本
- 真反例(True Negative,TN):预测为负样本,真实也为负样本
- 假正例(False Positive,FP):预测为正样本,真实为负样本
- 假反例(False Negative,FN):预测为负样本,真实为正样本
3.准确率(Accuracy)
准确率是所有样本中预测正确的样本占比,其公式如下:
A
c
c
u
r
a
c
y
=
T
P
+
T
N
T
P
+
F
P
+
T
N
+
F
N
Accuracy=\frac{TP+TN}{TP+FP+TN+FN}
Accuracy=TP+FP+TN+FNTP+TN
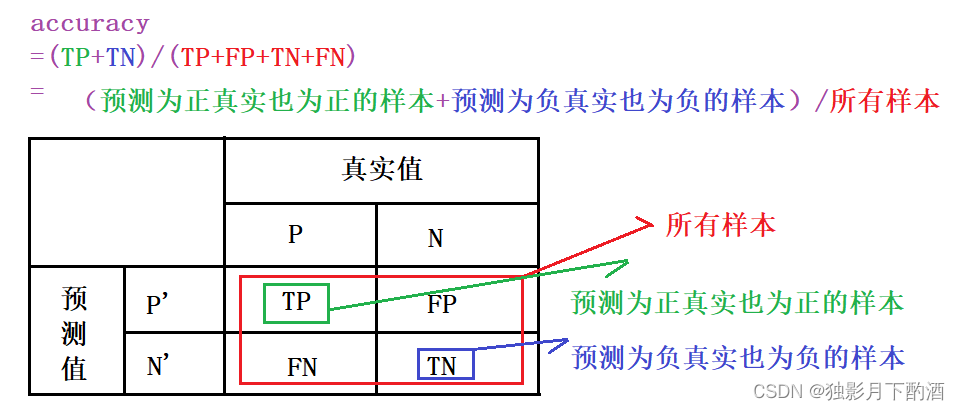
准确率有一个明显的弊端问题,就是在数据的类别不均衡,特别是有极偏的数据存在的情况下,准确率这个评价指标是不能客观评价算法的优劣的。
如:在测试集中,有1000个测试样本,999个反例,只有1个正例。如果模型对任意一个测试样本都预测是反例,那么模型的准确率就是99%,从数值上看是非常好的,但事实上,这样的算法没有任何的预测能力。
4.精准率(precision)、召回率(recall)
4.1 精准率
精准率(Precision)又称查准率,它是针对预测结果而言的,它的含义是在所有被预测为正的样本中实际为正的样本的概率,即在预测为正样本的结果中,有多少把握可以预测正确,其公式如下:
P
r
e
c
i
s
i
o
n
=
T
P
T
P
+
F
P
Precision=\frac{TP}{TP+FP}
Precision=TP+FPTP
精准率和准确率是完全不同的两个概念。精准率代表对正样本结果中的预测准确程度,而准确率则代表整体的预测准确程度,既包括正样本,也包括负样本。

4.2 召回率
召回率(Recall)又称查全率,它是针对原样本而言的,它的含义是在实际为正的样本中被预测为正样本的概率,其公式如下:
R
e
c
a
l
l
=
T
P
T
P
+
F
N
Recall=\frac{TP}{TP+FN}
Recall=TP+FNTP
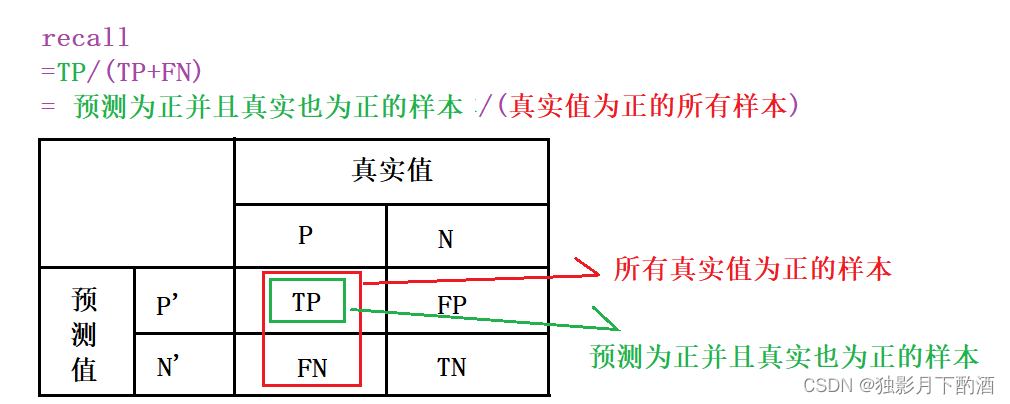
引用Wiki中的图,帮助说明下二者的关系。
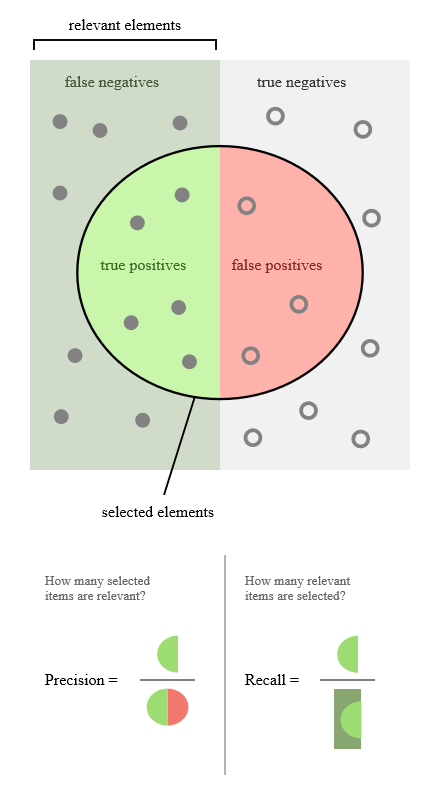
在不同的应用场景下,关注点不同,例如,在预测股票的时候,更关心Precision,即预测升的那些股票里,真的升了有多少,因为那些预测升的股票都是投钱的。而在预测病患的场景下,更关注Recall,即真的患病的那些人里预测错了情况应该越少越好。
Precision和Recall是一对此消彼长的度量。例如在推荐系统中,想让推送的内容尽可能用户全都感兴趣,那只能推送把握高的内容,这样就漏掉了一些用户感兴趣的内容,Recall就低了;如果想让用户感兴趣的内容都被推送,那只有将所有内容都推送上,宁可错杀一千,不可放过一个,这样Precision就很低了。
4.3 P-R曲线
根据学习器的预测结果(一般为一个实值或概率)对测试样本进行排序,将最可能是“正例”的样本排在前面,最不可能是“正例”的排在后面,按此顺序逐个把样本作为“正例”进行预测,每次计算出当前的P值和R值。
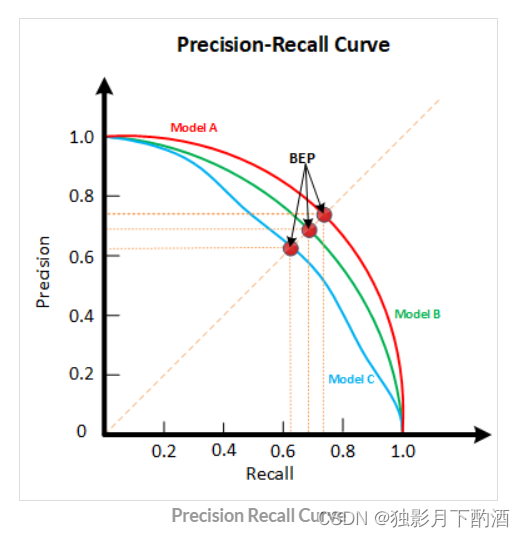
P-R曲线评估:
若一个学习器A的P-R曲线被另一个学习器B的P-R曲线完全包住,则称:B的性能优于A。若A和B的曲线发生了交叉,则谁的曲线下的面积大,谁的性能更优。但一般来说,曲线下的面积是很难进行估算的,所以衍生出了“平衡点”(Break-Event Point,简称BEP),即当P=R时的取值,平衡点的取值越高,性能更优。
5.F1-Score
通常使用Precision和Recall这两个指标,来评价二分类模型的效果。但是,Precision和Recall指标有时是此消彼长的,即精准率高了,召回率就下降。为了兼顾Precision和Recall,最常见的方法就是F-Measure,又称F-Score。F-Measure是P和R的加权调和平均,计算公式如下:
1
F
β
=
1
1
+
β
2
⋅
(
1
P
+
β
2
R
)
1
F
β
=
(
1
+
β
2
)
×
P
×
R
(
β
2
×
P
)
+
R
\begin{align} \frac{1}{F_\beta}=\frac{1}{1+\beta^2}·(\frac{1}{P}+\frac{\beta^2}{R})\\[2ex] \frac{1}{F_\beta}=\frac{(1+\beta^2)×P×R}{(\beta^2×P)+R} \end{align}
Fβ1=1+β21⋅(P1+Rβ2)Fβ1=(β2×P)+R(1+β2)×P×R
当
β
=
1
\beta=1
β=1时,也就是常说的F1-score,是P和R的调和平均,F1-Score的取值范围从0到1的,1代表模型的输出最好,0代表模型的输出结果最差 。当F1较高时,模型的性能越好。
1
F
1
=
1
2
⋅
(
1
P
+
1
R
)
F
1
=
2
×
P
×
R
P
+
R
\begin{align} \frac{1}{F_1}=\frac{1}{2}·(\frac{1}{P}+\frac{1}{R})\\[2ex] F1=\frac{2×P×R}{P+R} \end{align}
F11=21⋅(P1+R1)F1=P+R2×P×R
其中,P代表Precision,R代表Recall。
6.ROC曲线
6.1 ROC简介
ROC以及后面要讲到的AUC,是分类任务中非常常用的评价指标,本文将详细阐述。可能有人会有疑问,既然已经这么多评价标准,为什么还要使用ROC和AUC呢?
因为ROC曲线有个很好的特性:当测试集中的正负样本的分布变化的时候,ROC曲线能够保持不变。 在实际的数据集中经常会出现类别不平衡(Class Imbalance)现象,即负样本比正样本多很多(或者相反),而且测试数据中的正负样本的分布也可能随着时间变化,ROC以及AUC可以很好的消除样本类别不平衡对指标结果产生的影响。
另一个原因是,ROC和上面做提到的P-R曲线一样,是一种 不依赖于阈值(Threshold) 的评价指标,在输出为概率分布的分类模型中,如果仅使用准确率、精确率、召回率作为评价指标进行模型对比时,都必须时基于某一个给定阈值的,对于不同的阈值,各模型的Metrics结果也会有所不同,这样就很难得出一个很置信的结果。
在正式介绍ROC之前,我们还要再介绍两个指标,这两个指标的选择使得ROC可以无视样本的不平衡。这两个指标分别是:灵敏度(sensitivity)和特异度(specificity),也叫做真正率(TPR)和假正率(FPR),具体公式如下。
-
真正率(True Positive Rate , TPR),又称灵敏度:
T P R = 正样本预测正确数 正样本总数 = T P T P + F N TPR=\frac{正样本预测正确数}{正样本总数}=\frac{TP}{TP+FN} TPR=正样本总数正样本预测正确数=TP+FNTP
可以发现灵敏度和召回率是一模一样的 -
假负率(False Negative Rate , FNR) :
F N R = 正样本预测错误数 正样本总数 = F N T P + F N FNR=\frac{正样本预测错误数}{正样本总数}=\frac{FN}{TP+FN} FNR=正样本总数正样本预测错误数=TP+FNFN
- 假正率(False Positive Rate , FPR) :
F P R = 负样本预测错误数 负样本总数 = F P T N + F P FPR=\frac{负样本预测错误数}{负样本总数}=\frac{FP}{TN+FP} FPR=负样本总数负样本预测错误数=TN+FPFP
- 真负率(True Negative Rate , TNR),又称特异度:
T N R = 负样本预测正确数 负样本总数 = T N T N + F P TNR=\frac{负样本预测正确数}{负样本总数}=\frac{TN}{TN+FP} TNR=负样本总数负样本预测正确数=TN+FPTN
细分析上述公式,我们可以可看出,灵敏度(真正率) T P R TPR TPR是正样本的召回率,特异度(真负率)TNR是负样本的召回率,而假负率 F N R = 1 − T P R FNR=1−TPR FNR=1−TPR、假正率 F P R = 1 − T N R FPR=1−TNR FPR=1−TNR,上述四个量都是针对单一类别的预测结果而言的,所以对整体样本是否均衡并不敏感。举个例子:假设总样本中,90%是正样本,10%是负样本。在这种情况下我们如果使用准确率进行评价是不科学的,但是用TPR和TNR却是可以的,因为TPR只关注90%正样本中有多少是被预测正确的,而与那10%负样本毫无关系,同理,FPR只关注10%负样本中有多少是被预测错误的,也与那90%正样本毫无关系。这样就避免了样本不平衡的问题。
ROC曲线全称为受试者工作特征曲线(Receiver Operating Characteristic Curve)。ROC是一张图上的一条线(如下图所示),越靠近左上角的ROC曲线,模型的准确度越高,模型越理想;
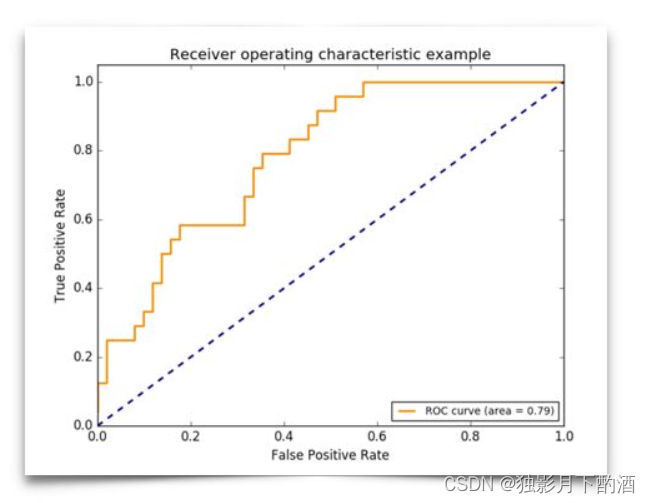
ROC曲线中,横轴是假阳率(False positive rate ,简称FPR),定义为 在所有真实的负样本中,被模型错误的判断为正例的比例 ,计算公式如下
F
P
R
=
F
P
F
P
+
T
N
FPR=\frac{FP}{FP+TN}
FPR=FP+TNFP
纵轴是真阳率(True Positive Rate,简称TPR),定义为 在所有真实的正样本中,被模型正确的判断为正例的比例,其实就是召回率,计算公式如下
T
P
R
=
T
P
T
P
+
F
N
TPR=\frac{TP}{TP+FN}
TPR=TP+FNTP
ROC曲线中,左下角的点所对应的是将所有样本判断为反例的情况,而右上角的点对应的是将所有样例判断为正例的情况;
6.2 ROC曲线的优点
阈值问题
ROC曲线也是通过遍历所有阈值来绘制整条曲线的。如果我们不断的遍历所有阈值,预测的正样本和负样本是在不断变化的,相应的在ROC曲线图中也会沿着曲线滑动。
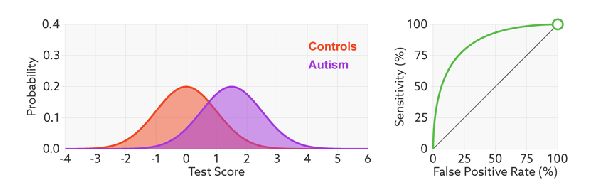
无视样本不平衡问题
当测试集中的正负样本的分布变化的时候,ROC曲线能够保持不变。
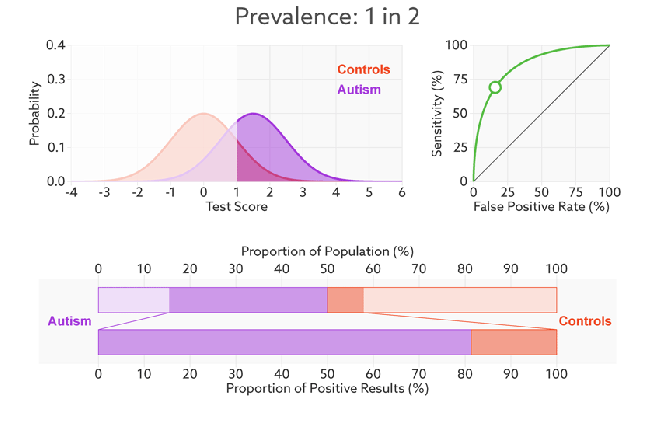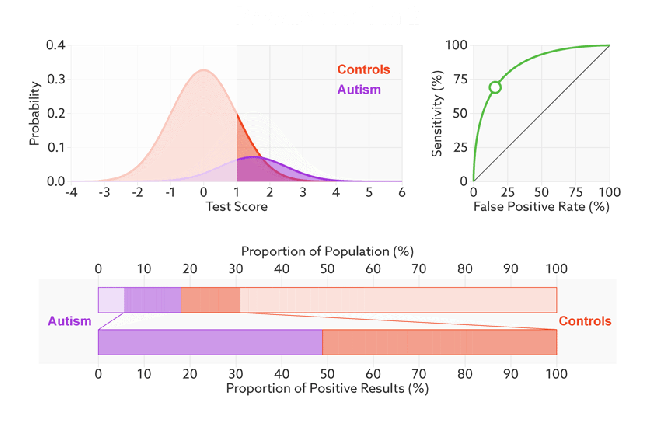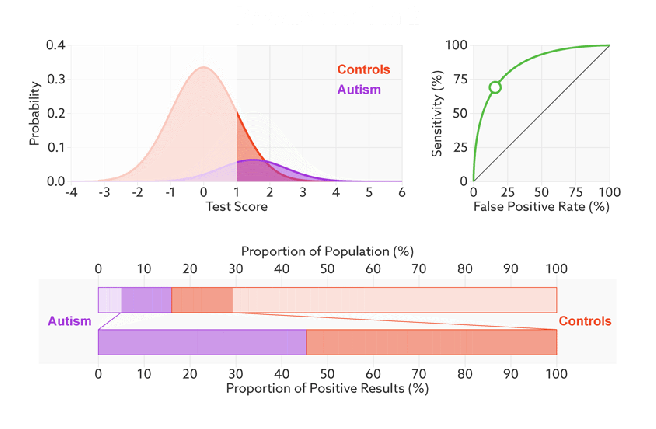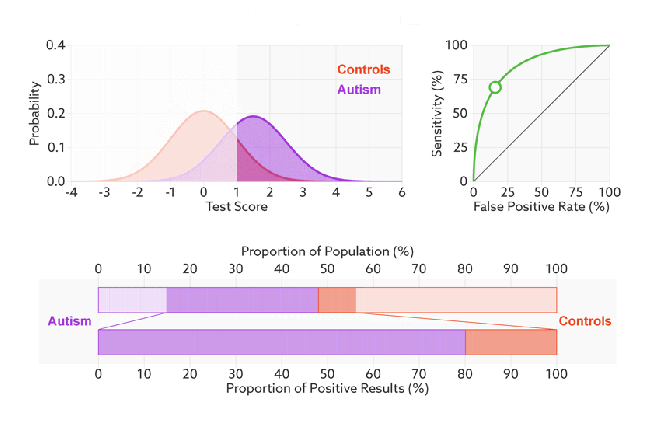
Q:如何判断一个模型的ROC曲线是好的呢?
FPR表示模型对于负样本误判的程度,而TPR表示模型对正样本召回的程度。我们所希望的当然是:负样本误判的越少越好,正样本召回的越多越好。所以总结一下就是TPR越高,同时FPR越低(即ROC曲线越陡),那么模型的性能就越好。
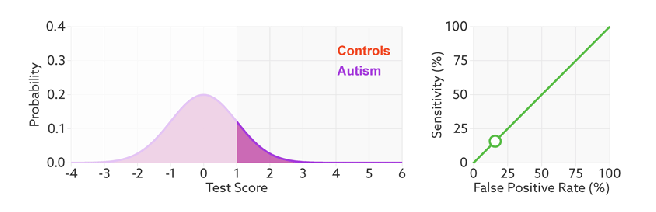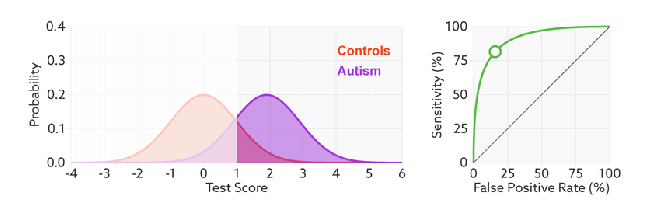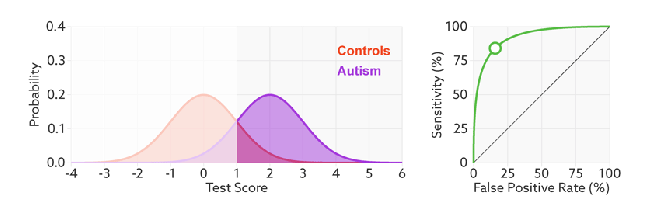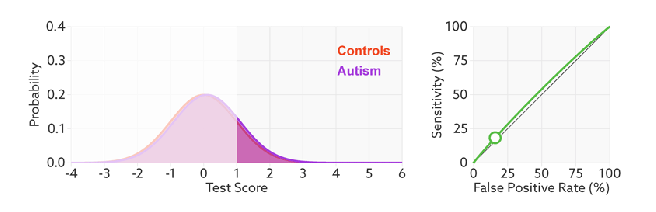
进行模型的性能比较时,与PR曲线类似,若一个模型A的ROC曲线被另一个模型B的ROC曲线完全包住,则称B的性能优于A。若A和B的曲线发生了交叉,则谁的曲线下的面积大,谁的性能更优。
6.3 如何绘制 ROC曲线
假设已经得出一系列样本被划分为正类的概率,然后按照大小排序,下图是一个示例,图中共有20个测试样本,“Class”一栏表示每个测试样本真正的标签(p表示正样本,n表示负样本),“Score”表示每个测试样本属于正样本的概率。
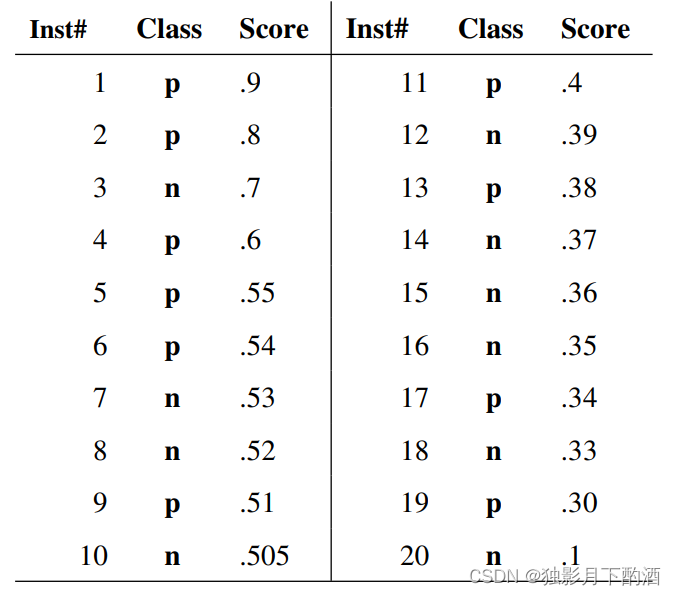
从高到低,依次将“Score”值作为阈值threshold,当测试样本属于正样本的概率大于或等于这个threshold时,认为它为正样本,否则为负样本。举例来说,对于图中的第4个样本,其“Score”值为0.6,那么样本1,2,3,4都被认为是正样本,因为它们的“Score”值都大于等于0.6,而其他样本则都认为是负样本。**每次选取一个不同的threshold,可以得到一组FPR和TPR,即ROC曲线上的一点。**这样一来,我们一共得到了20组FPR和TPR的值,将它们画在ROC曲线的结果如下图:
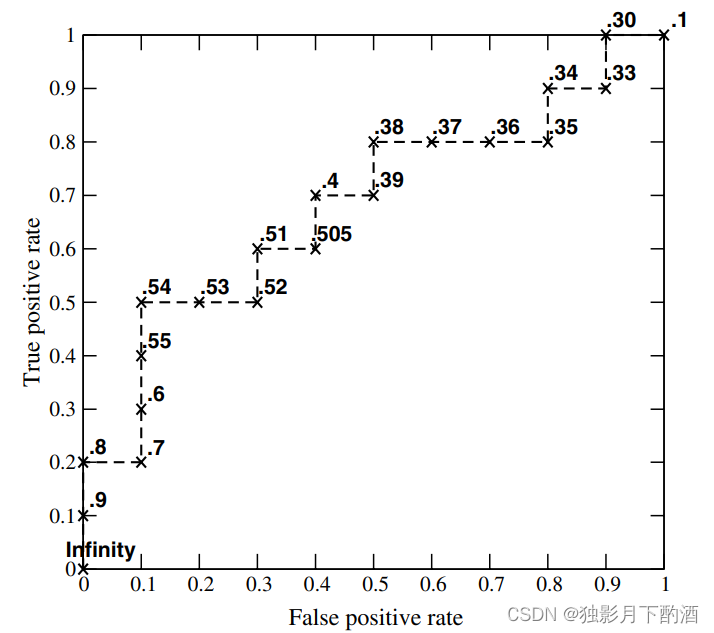
7.AUC
AUC (Area Under Curve) 被定义为ROC曲线下的面积,显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方,所以AUC的取值范围一般在0.5和1之间。
AUC对所有可能的分类阈值的效果进行综合衡量。首先AUC值是一个概率值,可以理解为随机挑选一个正样本以及一个负样本,分类器判定正样本分值高于负样本分值的概率就是AUC值。简言之,AUC值越大,当前的分类算法越有可能将正样本分值高于负样本分值,即能够更好的分类。
7.1 AUC的计算
7.1.1 计算方式1
计算出ROC曲线下面的面积,就是AUC的值。
由于我们的测试样本是有限的。我们得到的AUC曲线必然是一个阶梯状的。因此,计算的AUC也就是这些阶梯下面的面积之和。 先把score排序(假设score越大,此样本属于正类的概率越大),然后一边扫描就可以得到我们想要的AUC。但是,这么 做有个缺点,就是当多个测试样本的score相等的时,我们调整一下阈值,得到的不是曲线一个阶梯往上或者往右的延展,而是斜着向上形成一个梯形。此 时,我们就需要计算这个梯形的面积。由此可以发现使用这种方法计算AUC实际上是比较麻烦的。
7.1.2 计算方式2
从 Mann-Witney U统计角度解释:
AUC表示随机挑选一对正样本和负样本,当前分类算法依据计算出的score将正样本排在负样本前面的概率;反映了分类算法的排序能力。
由于样本的有限性,我们无法得到这个概率值,但是可以近似去估计它。最简单的方法就是利用频率去估计,即挑选出所有正负样本对,看看有多少样本对中,正样本的score大于负样本的score,如果成立就记一个,正样本的score等于负样本的score,记0.5个;记正样本为
x
+
x^+
x+,负样本为
x
−
x^-
x−,所有样本中正样本有
N
+
N^+
N+个,负样本有
N
−
N^-
N−个,正负样本的集合为
D
+
,
D
−
D^+,D^-
D+,D−,计算公式如下:
A
U
C
=
1
N
+
×
N
−
∑
x
+
∈
D
+
∑
x
−
∈
D
−
(
(
s
c
o
r
e
(
x
+
)
>
s
c
o
r
e
(
x
−
)
)
+
1
2
(
(
s
c
o
r
e
(
x
+
)
=
s
c
o
r
e
(
x
−
)
)
)
AUC=\frac{1}{N^+×N^-}\sum\limits_{x^+\in D^+}\sum\limits_{x^-\in D^-}\left((score(x^+)\gt score(x^-))+\frac{1}{2}((score(x^+)= score(x^-))\right)
AUC=N+×N−1x+∈D+∑x−∈D−∑((score(x+)>score(x−))+21((score(x+)=score(x−)))
举个栗子:
| inst# | class | score |
|---|---|---|
| 6 | p | 0.54 |
| 7 | n | 0.53 |
| 8 | n | 0.52 |
| 9 | p | 0.51 |
“Class”一栏表示每个测试样本真正的标签(p表示正样本,n表示负样本),“Score”表示每个测试样本属于正样本的概率。
正负样本对:(6,7),(6,8),(9,7),(9,8)
(6,7)中正样本被预测为正例的概率0.54,大于 负样本被预测为正例的概率0.53,记为1,同理(6,8)记为1;
(9,7)中正样本被预测为正例的概率0.51,大于 负样本被预测为正例的概率0.53,记为0,同理(9,8)记为0;
A
U
C
=
1
2
×
2
(
1
+
1
+
0
+
0
)
=
0.5
AUC=\frac{1}{2×2}(1+1+0+0)=0.5
AUC=2×21(1+1+0+0)=0.5
上述方法计算AUC的时间复杂度为
O
(
N
2
)
O(N^2)
O(N2),因为每一个样本都需要进行一次判断。
7.1.3 计算方式3
与计算方式2的计算方法是一样的,但是 复杂度减小了。 改进的方法:
① 对所有样本的score值从大到小排序
② 赋予每个样本一个Rank值,score最大真的样本Rank值为N
③ 对于score值相同的样本让它们的score值的平均值(比如A、B的score=0.7,Rank值分别为2,3,取平均值2.5)
计算公式如下:
A
U
C
=
1
N
+
×
N
−
(
∑
x
+
∈
D
+
R
a
n
k
(
x
+
)
−
1
2
N
+
(
N
+
+
1
)
)
AUC=\frac{1}{N^+×N^-}\left(\sum\limits_{x^+\in D^+}Rank(x^+)-\frac{1}{2}N^+(N^++1)\right)
AUC=N+×N−1(x+∈D+∑Rank(x+)−21N+(N++1))
理解:对样本进行Rank之后:
对于第一个正样本 x 1 + x^+_1 x1+和后面所有的样本配成 R a n k ( x 1 + ) − 1 Rank(x^+_1)-1 Rank(x1+)−1对,其中正样本的配对是不需要计算的,故而减去 N + − 1 N^+-1 N+−1(减1:自己无需和自己配对),故该样本对AUC的贡献为 R a n k ( x 1 + ) − N + Rank(x^+_1)-N^+ Rank(x1+)−N+。
对于第二个正样本 x 2 + x^+_2 x2+和后面所有的样本配成 R a n k ( x 1 + ) − 1 Rank(x^+_1)-1 Rank(x1+)−1对,其中正样本的配对是不需要计算的,故而减去 N + − 2 N^+-2 N+−2(减2:自己无需和自己配对,并且没有和前一个正样本配对),故该样本对AUC的贡献为 R a n k ( x 1 + ) − ( N + − 1 ) Rank(x^+_1)-(N^+-1) Rank(x1+)−(N+−1)。
以此类推:
对于第N个(最后一个)正样本
x
N
+
+
x^+_{N^+}
xN++和后面所有的样本配成
R
a
n
k
(
x
1
+
)
−
1
Rank(x^+_1)-1
Rank(x1+)−1对,其中正样本的配对是不需要计算的,故而减去0(减0:最后一个样本后面没有正样本了),故该样本对AUC的贡献为
R
a
n
k
(
x
1
+
)
−
1
Rank(x^+_1)-1
Rank(x1+)−1。
A
U
C
=
1
N
+
×
N
−
(
∑
i
=
1
N
R
a
n
k
(
x
i
+
)
−
(
N
+
−
i
+
1
)
)
=
1
N
+
×
N
−
(
∑
x
+
∈
D
+
R
a
n
k
(
x
+
)
−
1
2
N
+
(
N
+
+
1
)
)
\begin{align} AUC&=\frac{1}{N^+×N^-}\left(\sum\limits^N\limits_{i=1}Rank(x^+_i)-(N^+-i+1)\right)\\[2ex] &=\frac{1}{N^+×N^-}\left(\sum\limits_{x^+\in D^+}Rank(x^+)-\frac{1}{2}N^+(N^++1)\right) \end{align}
AUC=N+×N−1(i=1∑NRank(xi+)−(N+−i+1))=N+×N−1(x+∈D+∑Rank(x+)−21N+(N++1))
举个栗子:
| inst# | class | score | Rank | inst# | class | score | Rank |
|---|---|---|---|---|---|---|---|
| 1 | p | 0.9 | 20 | 11 | p | 0.4 | 10 |
| 2 | p | 0.8 | 19 | 12 | n | 0.39 | 9 |
| 3 | n | 0.7 | 18 | 13 | p | 0.38 | 8 |
| 4 | p | 0.6 | 17 | 14 | n | 0.37 | 7 |
| 5 | p | 0.55 | 16 | 15 | n | 0.36 | 6 |
| 6 | p | 0.54 | 15 | 16 | n | 0.35 | 5 |
| 7 | n | 0.53 | 14 | 17 | p | 0.34 | 4 |
| 8 | n | 0.52 | 13 | 18 | n | 0.33 | 3 |
| 9 | p | 0.51 | 12 | 19 | p | 0.3 | 2 |
| 10 | n | 0.5 | 11 | 20 | n | 0.1 | 1 |
“Class”一栏表示每个测试样本真正的标签(p表示正样本,n表示负样本),“Score”表示每个测试样本属于正样本的概率。
AUC的计算如下:
A
U
C
=
1
10
×
10
(
20
+
19
+
17
+
16
+
15
+
12
+
10
+
8
+
4
+
2
−
1
2
(
10
×
(
10
+
1
)
)
)
=
0.68
AUC=\frac{1}{10×10}(20+19+17+16+15+12+10+8+4+2-\frac{1}{2}(10×(10+1)))=0.68
AUC=10×101(20+19+17+16+15+12+10+8+4+2−21(10×(10+1)))=0.68
7.2 代码实现
import numpy as np
label_all = np.random.randint(0,2,[10,1]).tolist()
pred_all = np.random.random((10,1)).tolist()
print(label_all)
print(pred_all)
# 正样本的数量
posNum = len(list(filter(lambda s: s[0] == 1, label_all)))
if (posNum > 0):
negNum = len(label_all) - posNum
sortedq = sorted(enumerate(pred_all), key=lambda x: x[1])
posRankSum = 0
for j in range(len(pred_all)):
if (label_all[j][0] == 1):
posRankSum += list(map(lambda x: x[0], sortedq)).index(j) + 1
auc = (posRankSum - posNum * (posNum + 1) / 2) / (posNum * negNum)
print("auc:", auc)
8.总结
- 混淆矩阵是一种特定的矩阵用来呈现算法性能的可视化效。
- 准确率是预测正确的结果占总样本的百分比,当样本不平衡的时候,准确率就会失效。
- 精准率是在所有被预测为正的样本中实际为正的样本的概率。
- 精准率代表对正样本结果中的预测准确程度,而准确率则代表整体的预测准确程度,既包括正样本,也包括负样本。
- 召回率是在实际为正的样本中被预测为正样本的概率。
- 精确率和召回率是一对此消彼长的度量。
- 当测试集中的正负样本的分布变化的时候,ROC曲线能够保持不变;同时ROC曲线 是一种不依赖于阈值(Threshold)的评价指标。
- AUC的物理意义:随机挑选一个正样本以及一个负样本,分类器判定正样本分值高于负样本分值的概率,反映的是模型对样本的序关系。
本文仅作为个人学习记录所用,不作为商业用途,谢谢理解。
参考:https://zhuanlan.zhihu.com/p/37522326