剑指 Offer 51. 数组中的逆序对

难度：$hard$

---

题目描述

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

示例 1:

输入: [7,5,6,4]
输出: 5

限制：

$0<=数组长度<=50000$

---

算法

(归并排序)

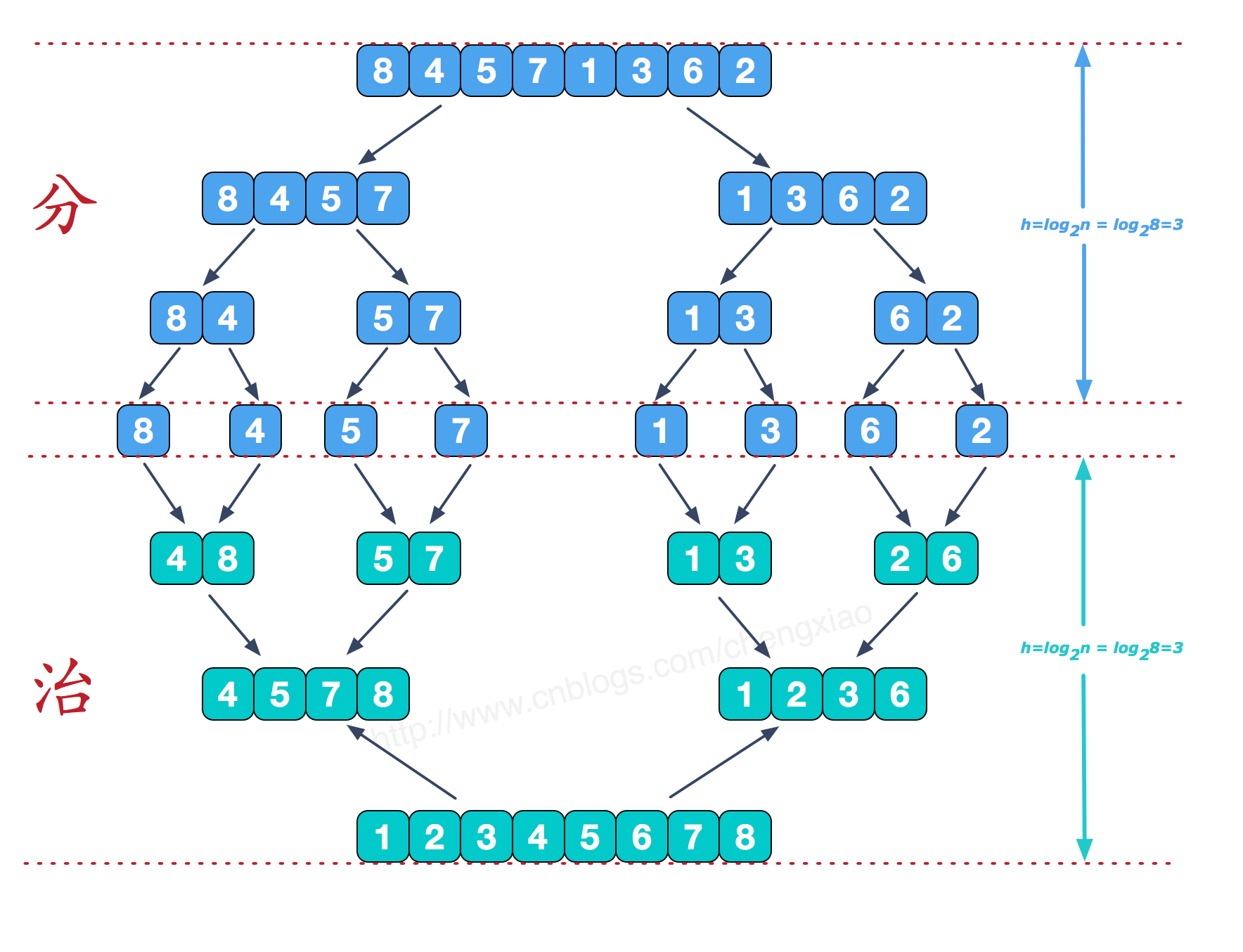
首先先看一张图：

1. 逆序对的定义：

对于数列的第 i 个和第 j 个元素，如果满足 i < j 且 a[i] > a[j]，则其为一个逆序对。
重要的地方在于，一个元素可以不只是在一个逆序对中存在。如果 k > j > i 且 a[i] > a[j] > a[k]，那么这里
有两个含 a[i] 的逆序对，分别是 (a[i], a[j]) 和 (a[i], a[k]), a[i]是可以使用多次的。
(太长不看)
举个栗子：

num:  2 3 4 5 6 1
id :  0 1 2 3 4 5

一句话概括就是求当前数组中存在几个比当前位置大的，（或者后面有几个数字比他小的） 加上2在第一个位置，后面比它小的数字是1，所以2的逆序对是(2， 1), 同理(3, 1) (4, 1) (5, 1) (6, 1)
答案是5。

2. 分析问题：

采用分治法来求解问题，为什么不是树状数组呢~~（buhui）~~,因为分治法求解此题比较简单。
按照y总的说法：我们将序列从中间分开，将逆序对分成三类：

1. 两个元素都在左边；
2. 两个元素都在右边；
3. 两个元素一个在左一个在右；

算法的大致框架为：

1. 递归算$左边$的；
2. 递归算$右边$的；
3. 算$一个左一个右$的；
4. 把三个结果加在一起
   

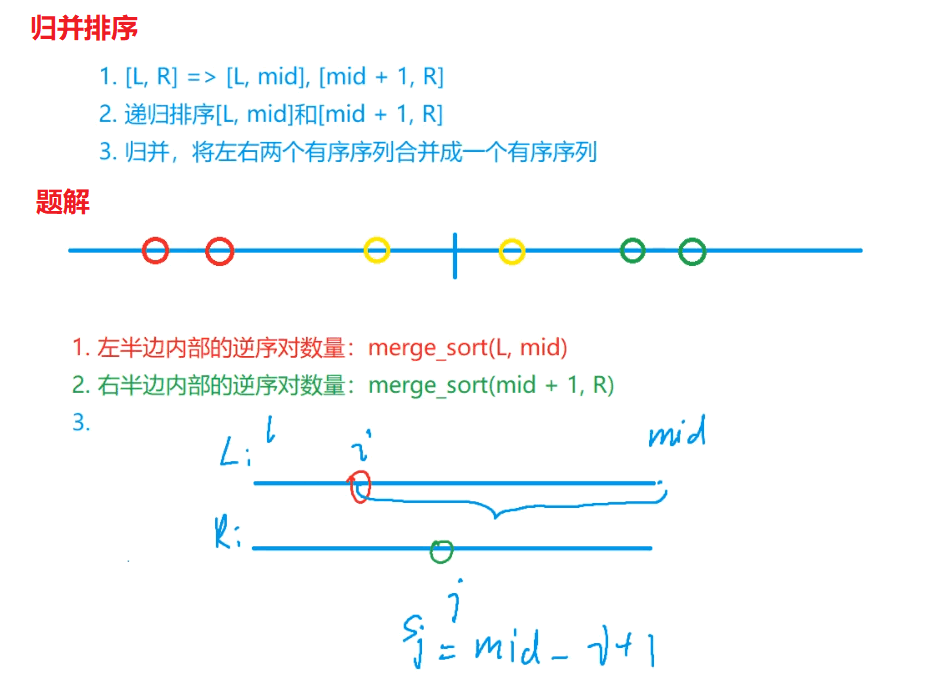
3. 问题详解：

1. 在一些题解中说到可以不用计算前两种情况，只需要看第三种情况，我的理解是:需要真正知道归并排序在做什么。这就是我们上面的那张图，归并排序分为两个大步骤；$分$和$治$，从上面的栗子中我们看出，分的步骤会把所有的数组分为一个单独的数字，所以也就解释了为什么不需要考虑前两种情况，最种都会到第三中情况上，因为只有每组只有一个数字，它没有人同组，1就是1，怎么变成2，我就吃了一碗粉，为什么付两碗的钱。所以最终都是会变成第三种情况。
2. 下面解释治.
   
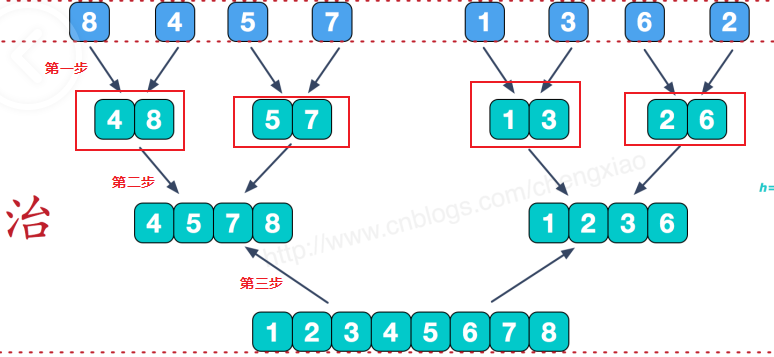
3. 第一步对元素进行排序，可以看到直接是求两个单独元素的逆序对，如果是逆序对，答案ans++,然后合并两个数字变成一个有序的数组，
4. 第二步，在对两个分组的数字进行求逆序对，此时没有到只剩下两个分组的情况，可以把这些步骤看作是内部之间求逆序对。
5. 第三步就是两个分组求逆序对。可以看到此时前后两个分组都是有序的，前面的数组的下边为l..mid，后面的下标为mid + 1...r，我们可以在归并的时候是需要把两个数组的值重新赋值到原数组中的，所以就可以比较两个数组的值，也就是可以求逆序对。如果A数组的值q[i] 大于B数组的值q[j]，代表在A数组中i~mid都是大于q[j]的，所以对于q[j]来说他的逆序对数量为mid - i + 1,同理，其他的逆序对也可以这么求。

复杂度分析

• 时间复杂度：$O(nlogn)$，其中 $n$ 是链表的长度。需要遍历链表一次

• 空间复杂度 : $O(n)$，因为归并排序需要用到一个临时数组。

C++ 代码

class Solution {
public:
    int reversePairs(vector<int>& nums) {
        return merge_sort(nums, 0, nums.size() - 1);
    }

    int merge_sort(vector<int>& nums, int l, int r)
    {
        if (l >= r) return 0;
        int mid = (l + r) / 2;
        // 分
        int res = merge_sort(nums, l, mid) + merge_sort(nums, mid + 1, r);
        // 并
        int i = l, j = mid + 1, k = 0;
        vector<int> temp;
        while (i <= mid && j <= r)
        {
            if (nums[i] <= nums[j]) temp.push_back(nums[i ++]);
            else
            {
                res += mid - i + 1;
                temp.push_back(nums[j ++]);
            }
        }

        while (i <= mid) temp.push_back(nums[i ++]);
        while (j <= r) temp.push_back(nums[j ++]);

        i = l;
        for (auto x : temp) nums[i ++] = x;

        return res;
    }
};

---