原文:Numpy Essentials
协议:CC BY-NC-SA 4.0
译者:飞龙
一、NumPy 简介
“我宁愿使用通用语言进行数学运算,也不愿尝试使用数学语言进行通用编程。”
– John D Cook
在过去的十年中,Python 已成为科学计算中最受欢迎的编程语言之一。 其成功的原因很多,随着您着手本书,这些原因将逐渐变得明显。 与许多其他数学语言(例如 MATLAB,R 和 Mathematica)不同,Python 是一种通用编程语言。 因此,它为构建科学应用并将其进一步扩展到任何商业或学术领域提供了合适的框架。 例如,考虑一个(某种)简单的应用,该应用要求您编写软件并预测博客文章的受欢迎程度。 通常,这些是您要执行此操作的步骤:
- 生成博客文章及其相应评级的语料库(假设此处的评级可适当量化)。
- 制定一个模型,该模型根据与博客文章相关的内容和其他数据生成评分。
- 根据您在步骤 1 中找到的数据来训练模型。请继续进行此操作,直到您对模型的可靠性充满信心为止。
- 将模型部署为 Web 服务。
通常,在执行这些步骤时,您会发现自己在不同的软件栈之间跳转。 第 1 步需要进行大量的网页抓取。 Web 抓取是一个非常普遍的问题,几乎每种编程语言都有一些工具可以抓取 Web(如果您已经在使用 Python,则可能会选择 BeautifulSoup 或 Scrapy)。 第 2 步和第 3 步涉及解决机器学习问题,并且需要使用复杂的数学语言或框架,例如 Weka 或 MATLAB,这只是提供机器学习功能的众多工具中的少数几种。 同样,步骤 4 可以使用许多不同的工具以多种方式实现。 没有一个正确的答案。 由于这个问题已经被许多科学家和软件开发人员充分研究和解决(在一定程度上),因此,找到可行的解决方案并不困难。 但是,诸如稳定性和可伸缩性之类的问题可能会严重限制您在问题的每个步骤中对编程语言,Web 框架或机器学习算法的选择。 这就是 Python 胜过大多数其他编程语言的地方。 前面的所有步骤(以及更多步骤)都只能使用 Python 和一些第三方 Python 库来完成。 这种使用 Python 开发软件的灵活性和便捷性正是使其成为科学计算生态系统的理想宿主。 在 Ivan Idris 所写的《Python 数据分析》中可以找到关于 Python 作为成熟的应用开发语言的非常有趣的解释。精确地讲,Python 是一种用于快速原型制作的语言,并且由于其随着时间的推移而获得了广泛的科学生态系统,它也被用于构建生产质量的软件。 这个生态系统的基础是 NumPy。
数字 Python(NumPy)是 Numeric 包的后续产品。 它最初由 Travis Oliphant 编写,是 Python 科学计算环境的基础。 它在 2005 年初从功能更广泛的 SciPy 模块分支出来,并于 2006 年中首次稳定发布。 从那以后,它在从事数学,科学和工程领域的 Python 爱好者中越来越受欢迎。 本书的目的是使您对 NumPy 足够熟悉,以便您能够使用它并使用它构建复杂的科学应用。
Python 科学栈
让我们首先简要浏览一下 Python 科学计算(SciPy)栈。
注意
请注意,SciPy 可能意味着很多事情:名为 scipy 的 Python 模块,整个 SciPy 栈,或在世界各地举行的有关科学 Python 的三个会议中的任何一个。

Figure 1: The SciPy stack, standard, and extended libraries
IPython 的主要作者 Fernando Perez 在 2012 年加拿大 PyCon 的主题演讲中说:
“科学计算的发展不仅仅是因为软件的发展,而且还因为我们作为科学家所做的不仅仅是浮点运算。”
这正是 SciPy 栈拥有如此丰富的功能的原因。 大多数 SciPy 栈的演进是由试图以通用编程语言解决科学和工程问题的科学家和工程师团队推动的。 对 NumPy 为什么如此重要的一个单方面的解释是,它提供了科学计算中大多数任务所必需的核心多维数组对象。 这就是为什么它是 SciPy 栈的根本原因。 NumPy 使用久经考验的科学库,提供了一种简单的方法来与遗留的 Fortran 和 C/C++ 数字代码对接,我们知道该库已经运行了数十年。 全世界的公司和实验室都使用 Python 将已经存在很长时间的遗留代码粘合在一起。 简而言之,这意味着 NumPy 允许我们站在巨人的肩膀上。 我们不必重新发明轮子。 这是每个其他 SciPy 包的依赖项。 NumPy ndarray对象实际上是下一章的主题,它是 Pythonic 接口,用于用 Fortran,C 和 C++ 编写的库所使用的数据结构。 实际上,NumPy ndarray对象使用的内部内存布局实现 C 和 Fortran 布局。 这将在以后的章节中详细讨论。
栈的下一层包括 SciPy,matplotlib,IPython(Python 的交互式外壳;我们将在整本书中将其用作示例,其安装和使用的详细信息将在后面的部分中提供)以及 SymPy 模块。 SciPy 提供了生态系统主要部分所依赖的大部分科学和数值功能。 Matplotlib 是 Python 中的事实绘图和数据可视化库。 IPython 是用于 Python 中科学计算的日益流行的交互式环境。 实际上,该项目已经进行了如此积极的开发并享有很高的知名度,以至于它不再局限于 Python,而且将其功能扩展到其他科学语言,尤其是 R 和 Julia。 栈中的这一层可以看作是 NumPy 的面向核心数组的功能与栈较高层提供的特定于域的抽象之间的桥梁。 这些特定于领域的工具通常称为 SciKits,受欢迎的工具包括 scikit-image(图像处理),scikit-learn(机器学习),statsmodels(统计信息),pandas(高级数据分析)等等。 由于科学的 Python 社区非常活跃,因此几乎不可能在 Python 中列出每个科学包,并且针对大量的科学问题总是有很多发展。 跟踪项目的最佳方法是参与社区。 加入邮件列表,编写代码,将软件用于日常计算需求并报告错误,这非常有用。 本书的目标之一是使您足够感兴趣,以积极地参与科学的 Python 社区。
NumPy 数组的必要性
初学者提出的一个基本问题是。 为什么数组对于科学计算完全必要? 当然,可以对任何抽象数据类型(如列表)执行复杂的数学运算。 答案在于数组的众多属性,这些属性使它们明显更有用。 在本节中,让我们看一下其中的一些属性,以强调为什么诸如 NumPy ndarray对象之类的东西根本不存在。
表示矩阵和向量
矩阵和向量的抽象数学概念是许多科学问题的核心。 数组为这些概念提供了直接的语义链接。 确实,每当一本数学文献提到矩阵时,就可以安全地将数组视为代表矩阵的软件抽象。 在科学文献中,A[ij]等表达式通常用于表示数组A的第i行和j列的元素。 NumPy 中的相应表达将简单地是A[i, j]。 对于矩阵运算,NumPy 数组还支持向量化(有关详细信息,请参见第 3 章,“使用 Numpy 数组”),这大大加快了执行速度。 向量化使代码更简洁,更易于阅读,并且更类似于数学符号。 像矩阵一样,数组也可以是多维的。 数组的每个元素都可以通过一组称为索引的整数来寻址,而使用整数集访问数组的元素的过程称为索引。 确实可以在不使用数组的情况下实现此功能,但这将很麻烦并且非常不必要。
效率
效率在软件中可能意味着很多事情。 该术语可用于指代程序的执行速度,其数据检索和存储性能,其内存开销(程序执行时消耗的内存)或其整体吞吐量。 就几乎所有这些特性而言,NumPy 数组都比大多数其他数据结构要好(只有少数例外,例如 pandas,DataFrame或 SciPy 的稀疏矩阵,我们将在后面的章节中介绍)。 由于 NumPy 数组是静态类型且同质的,因此可以用编译语言实现快速数学运算(默认实现使用 C 和 Fortran)。 效率(在同类数组上运行快速算法的可用性)使 NumPy 变得流行且重要。
易于开发
NumPy 模块是用于数学任务的现成功能的强大平台。 它极大地增加了 Python 的开发难度。 以下是该模块包含的内容的简要概述,我们将在本书中探讨其中的大部分内容。 有关 NumPy 模块的详细介绍,请参见 Travis Oliphat 所写的权威的《NumPy 指南》。 NumPy API 非常灵活,以至于科学 Python 社区已广泛采用它作为构建科学应用的标准 API。 可以参考 Van Der Walt 等人所写的《NumPy 数组:有效数值计算的结构》:
| 子模块 | 内容 |
|---|---|
numpy.core | 基本对象 |
lib | 其他工具 |
linalg | 基本线性代数 |
fft | 离散傅立叶变换 |
random | 随机数生成器 |
distutils | 增强的构建和发行版 |
testing | 单元测试 |
f2py | Fortran 代码的自动包装 |
学术界和工业界的 NumPy
有人说,如果您在时代广场站足够长的时间,就会遇到世界上每个人。 现在,您必须已经确信 NumPy 是 SciPy 的时代广场。 如果您使用 Python 编写科学应用,那么不需深入研究 NumPy,您将无能为力。 图 2 显示了不同抽象级别的科学计算中 SciPy 的范围。 红色箭头表示科学软件应具有的各种低级功能,蓝色箭头表示利用这些功能的不同应用领域。 配备 SciPy 栈的 Python 处于提供这些功能的语言的最前沿。
Google 学术搜索 NumPy 会返回近 6,280 个结果。 其中一些是有关 NumPy 和 SciPy 栈本身的论文和文章,还有许多是有关 NumPy 在各种研究问题中的应用的。 学者们喜欢 Python,SciPy 栈作为世界上无数大学和研究实验室中科学编程的主要语言越来越受欢迎,这说明了 Python。 许多科学家和软件专业人员的经验已发布在 Python 网站上:
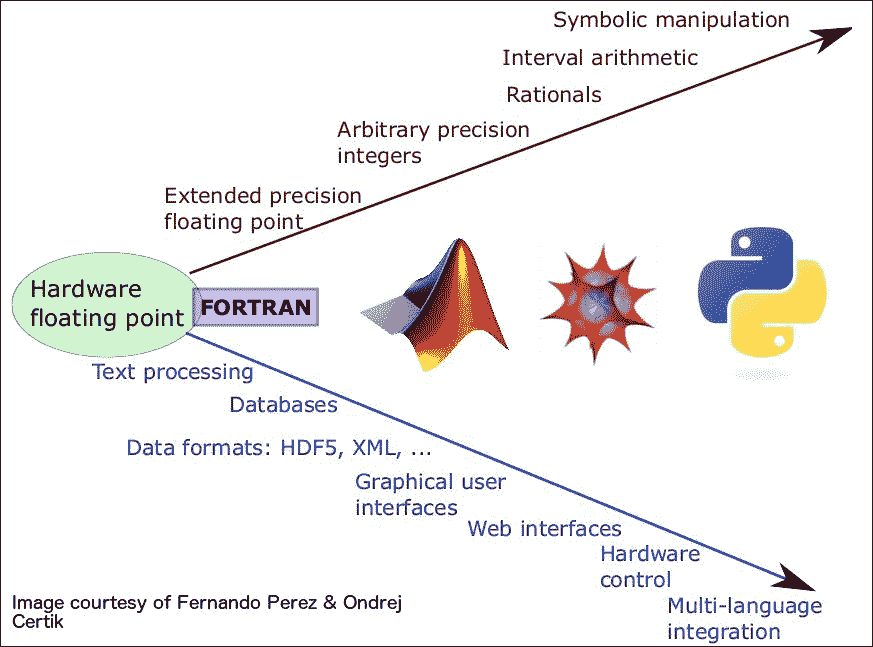
Figure 2: Python versus other languages
书中使用的代码约定
现在,Python 和 NumPy 的信誉已经确立,让我们动手吧。
本书中所有 Python 代码使用的默认环境是 IPython。 下一节将介绍如何安装 IPython 和其他工具。 在整本书中,您只需在命令窗口或 IPython 提示符下输入输入即可。 除非另有说明,否则code将引用 Python 代码,command将引用 bash 或 DOS 命令。
所有 Python 输入代码都将按照以下代码段格式进行格式化:
In [42]: print("Hello, World!")
上一小段中的In [42]:表示这是第 42 个 IPython 会话输入。 同样,所有命令行输入的格式将如下:
$ python hello_world.py
在 Windows 系统上,相同的命令如下所示:
C:\Users\JohnDoe> python hello_world.py
为了保持一致,无论操作系统如何,$符号都将用于表示命令行提示符。 诸如C:\Users\JohnDoe>之类的提示将不会出现在书中。 通常,$符号表示 Unix 系统上的 bash 提示,但是相同的命令(无需键入实际的美元符号或任何其他字符)也可以在 Windows 上使用。 但是,如果您使用的是 Cygwin 或 Git Bash,则也应该能够在 Windows 上使用 Bash 命令。
请注意,如果您在 Windows 上安装 Git,则默认情况下 Git Bash 可用。
安装要求
让我们看一下在继续之前需要设置的各种要求。
使用 Python 发行版
本书所需的三个最重要的 Python 模块是 NumPy,IPython 和 matplotlib。 在本书中,代码基于 Python 3.4 / 2.7 兼容版本,NumPy 1.9 版本和 matplotlib 1.4.3。 安装这些要求(甚至更多)的最简单方法是安装完整的 Python 发行版,例如 Enthought Canopy,EPD,Anaconda 或 PythonXY。 一旦安装了其中任何一个,就可以安全地跳过本节的其余部分,并且应该可以开始了。
注意
面向 Canopy 用户的注意事项:可以使用 Canopy GUI,该 GUI 包括嵌入式 IPython 控制台,文本编辑器和 IPython Notebook 编辑器。 使用命令行时,为了获得最佳效果,请使用 Canopy 的“工具”菜单中的 Canopy 终端。
Windows OS 用户注意事项:除了 Python 发行版,您还可以从 Ghristoph Gohlke 网站安装预构建的 Windows python 扩展包。
使用 Python 包管理器
您还可以使用以下命令之一使用 Python 包管理器(例如 enpkg,Conda,PIP 或 EasyInstall)来安装需求。 将numpy替换为您要安装的其他任何包名称,例如ipython,matplotlib等:
$ pip install numpy
$ easy_install numpy
$ enpkg numpy # for Canopy users
$ conda install numpy # for Anaconda users
使用本机包管理器
如果要使用的 Python 解释器随操作系统一起提供,而不是第三方安装,则您可能更喜欢使用特定于操作系统的包管理器,例如 aptitude,yum 或 Homebrew。 下表说明了包管理器和用于安装 NumPy 的相应命令:
| 包管理器 | 命令 |
|---|---|
apt | $ sudo apt-get install python-numpy |
yum | $ yum install python-numpy |
brew | $ brew install numpy |
请注意,在带有 Homebrew 的 OS X 系统上安装 NumPy(或任何其他 Python 模块)时,Python 最初应与 Homebrew 一起安装。
有关详细的安装说明,请参见 NumPy,IPython 和 matplotlib 的相应网站。 作为预防措施,要检查 NumPy 是否已正确安装,请打开 IPython 终端并键入以下命令:
In [1]: import numpy as np
In [2]: np.test()
如果第一个语句看起来什么也没做,则表明这是一个好兆头。 如果执行时没有任何输出,则表示已安装 NumPy 并将其正确导入到 Python 会话中。 第二条语句运行 NumPy 测试套件。 这不是绝对必要的,但永远不要太谨慎。 理想情况下,它应运行几分钟并产生测试结果。 它可能会生成一些警告,但是这些都不会引起警报。 如果您愿意,也可以运行 IPython 和 matplotlib 的测试套件。
注意
请注意,只有从源代码安装了 matplotlib 时,matplotlib 测试套件才能可靠运行。 但是,测试 matplotlib 并不是非常必要。 如果您可以导入 matplotlib 而没有任何错误,则表明它可以使用了。
恭喜你! 我们现在准备开始。
总结
在本章中,我们向自己介绍了 NumPy 模块。 我们了解了 NumPy 是如何为从事科学计算工作的人们提供的有用软件工具。 我们安装了完成本书其余部分所需的软件。
在下一章中,我们将介绍功能强大的 NumPy ndarray对象,向您展示如何有效地使用它。
二、NumPy ndarray对象
面向数组的计算是计算科学的核心。 这是大多数 Python 程序员都不习惯的。 尽管列表或字典的理解是相对于数组的,有时与数组的用法类似,但是在性能和操作上,列表/字典和数组之间还是存在巨大差异。 本章介绍了 NumPy 中的基本数组对象。 它涵盖了可以从 NumPy 数组的固有特性中收集的信息,而无需对该数组执行任何外部操作。
本章将涉及的主题如下:
numpy.ndarray以及如何使用它-面向基本数组的计算numpy.ndarray内存访问,存储和检索的性能- 索引,切片,视图和副本
- 数组数据类型
numpy.ndarray入门
在本节中,我们将介绍 numpy ndarray的一些内部结构,包括其结构和行为。 开始吧。 在 IPython 提示符中输入以下语句:
In [1]: import numpy as np
In [2]: x = np.array([[1,2,3],[2,3,4]])
In [3]: print(x)
NumPy 与其他模块(例如 Python 标准库中的math模块)中的函数共享其函数名称。 不建议使用如下所示的导入:
from numpy import *
因为它可能会覆盖全局名称空间中已经存在的许多函数,所以不建议这样做。 这可能会导致您的代码出现意外行为,并可能在其中引入非常细小的错误。 这也可能会在代码本身中造成冲突(例如 numPy 具有any并会与系统any关键字发生冲突),并可能在检查或调试一段代码时引起混乱。 因此,重要的是建议始终使用带有显式名称的导入 numPy,例如第一行中使用的np约定:-import numpy as np,这是用于导入目的的标准约定,因为它有助于开发人员找出函数的来源。 这可以避免大型程序中的许多混乱。
如我们将看到的,可以用多种方式创建 NumPy 数组。 创建数组的最简单方法之一是使用array函数。 注意,我们向函数传递了一个列表列表,组成列表的长度相等。 每个组成列表成为数组中的一行,并且这些列表的元素填充了结果数组的列。 array函数可以在列表甚至嵌套列表上调用。 由于此处输入的嵌套级别是 2,因此生成的数组是二维的。 这意味着可以使用两个整数集对数组进行索引。 计算数组维数的最简单方法是检查数组的ndim属性:
In [4]: x.ndim
Out [4]: 2
这也可以通过检查数组的shape属性以其他(间接)方式来实现。 数组的维数将等于您在shape属性中看到的数字。 (但是请注意,这并不是shape属性的目的。):
In [5]: x.shape
Out [5]: (2, 3)
这意味着该数组具有两行三列。 重要的是要注意,与 MATLAB 和 R 不同,NumPy 数组的索引是从零开始的。 也就是说,NumPy 数组的第一个元素索引为零,而最后一个元素索引为整数n-1,其中n是数组沿相应维度的长度。 因此,对于我们刚刚创建的数组,可以使用一对零来访问数组左上角的元素,并且可以使用索引来访问右下角的元素(1,2):
In [6]: x
Out[6]:
array([[1, 2, 3],
[2, 3, 4]])
In [7]: x[0,0]
Out[7]: 1
In [8]: x[1,2]
Out[8]: 4
ndarray对象具有许多有用的方法。 要获取可以在ndarray对象上调用的方法的列表,请在 IPython 提示符下键入array变量(在前面的示例中为x),然后按TAB。 这应该列出该对象可用的所有方法。 作为练习,尝试与其中一些玩耍。
数组索引和切片
NumPy 为数组提供了强大的索引功能。 NumPy 中的索引功能变得如此流行,以至于其中许多功能又重新添加到 Python 中。
在许多方面,为 NumPy 数组建立索引与为列表或元组建立索引非常相似。 存在一些差异,随着我们的进行,这些差异将变得显而易见。 首先,让我们创建一个尺寸为100 x 100的数组:
In [9]: x = np.random.random((100, 100))
简单的整数索引的工作方式是在一对方括号内键入索引,然后将其放置在数组变量旁边。 这是一种广泛使用的 Python 构造。 具有__getitem__方法的任何对象都将响应此类索引。 因此,要访问第 42 行和第 87 列中的元素,只需键入:
In [10]: y = x[42, 87]
像列表和其他 Python 序列一样,也支持使用冒号为一系列值建立索引。 以下语句将打印x矩阵的第k行。
In [11]: print(x[k, :])
冒号可以被认为是所有元素的字符。 因此,前面的语句实际上意味着打印第k行的所有字符。 同样,可以使用x[:,k]访问列。 反转数组也类似于反转列表,例如x[::-1]。
数组的索引部分也称为数组的切片,它创建端口或整个数组的副本(我们将在后面的部分中介绍副本和视图) 。 在数组的上下文中,单词“切片”和“索引”通常可以互换使用。
下图显示了不同切片和索引技术的非常简洁的概述:

ndarray的内存布局
ndarray对象的一个特别有趣的属性是flags。 输入以下代码:
In [12]: x.flags
它应该产生如下内容:
Out[12]:
C_CONTIGUOUS : True
F_CONTIGUOUS : False
OWNDATA : True
WRITEABLE : True
ALIGNED : True
UPDATEIFCOPY : False
flags属性保存有关数组的内存布局的信息。 输出中的C_CONTIGUOUS字段指示该数组是否为 C 样式数组。 这意味着该数组的索引就像 C 数组一样完成。 在 2D 数组的情况下,这也称为行优先索引。 这意味着,当在数组中移动时,行索引将首先增加,然后列索引将增加。 在多维 C 样式数组的情况下,最后一个维度首先递增,然后是最后一个,但最后一个递增,依此类推。
同样,F_CONTIGUOUS属性指示该数组是否为 Fortran 样式的数组。 据说这样的数组具有列主索引(R,Julia 和 MATLAB 使用列主数组)。 这意味着,当在数组中移动时,第一个索引(沿着列)首先增加。
知道索引样式之间的差异很重要,尤其是对于大型数组,因为如果以正确的方式应用索引,则可以大大加快对数组的操作。 让我们通过练习来演示这一点。
声明一个数组,如下所示:
In [13]: c_array = np.random.rand(10000, 10000)
这将产生一个名为c_array的变量,它是一个二维数组,其随机数为一亿。 (我们使用了 NumPy 中random子模块中的rand函数,我们将在下一部分中对其进行处理)。 接下来,从c_array创建一个 Fortran 样式的数组,如下所示:
In [14]: f_array = np.asfortranarray(c_array)
您可以通过读取flags属性来分别检查c_array和f_array是否确实为 C 和 Fortran 风格。 接下来,我们定义以下两个函数:
In [15]: def sum_row(x):
'''
Given an array `x`, return the sum of its zeroth row.
'''
return np.sum(x[0, :])
In [16]: def sum_col(x):
'''
Given an array `x`, return the sum of its zeroth column.
'''
return np.sum(x[:, 0])
现在,让我们使用 IPython 的%timeit魔术函数在两个数组上测试这两个函数的性能:
注意
IPython 提供了一些魔术函数来帮助我们更好地理解代码。 有关更多详细信息,请参见这里。
In [17]: %timeit sum_row(c_array)
10000 loops, best of 3: 21.2 µs per loop
In [18]: %timeit sum_row(f_array)
10000 loops, best of 3: 157 µs per loop
In [19]: %timeit sum_col(c_array)
10000 loops, best of 3: 162 µs per loop
In [20]: %timeit sum_col(f_array)
10000 loops, best of 3: 21.4 µs per loop
如我们所见,对 C 数组的行求和比对其列求和要快得多。 这是因为,在 C 数组中,一行中的元素被放置在连续的内存位置中。 对于 Fortran 数组,情况恰好相反,其中列的元素布置在连续的内存位置中。
提示
请注意,确切的数字可能会因所使用的操作系统,RAM 和 Python 发行版而异,但是执行时间之间的相对顺序应保持不变。
这是一个重要的区别,它使您可以根据要执行的算法或运算的类型将数据适当地排列在一个数组中。 知道这种区别可以帮助您将代码加速几个数量级。
视图和副本
通过切片和索引访问数据主要有两种方法。 它们称为副本和视图:您可以直接从数组访问元素,也可以创建仅包含访问的元素的数组副本。 由于视图是原始数组的引用(在 Python 中,所有变量都是引用),因此修改视图也将修改原始数组。 对于副本,情况并非如此。
NumPy 其他例程中的may_share_memory函数可用于确定两个数组是彼此的副本还是彼此的视图。 尽管此方法在大多数情况下都能胜任,但由于使用启发式方法,因此并不总是可靠的。 它也可能返回错误的结果。 但是,出于介绍性目的,我们将其视为理所当然。
通常,切片数组会创建一个视图,对其进行索引会创建一个副本。 让我们通过一些代码片段研究这些差异。 首先,让我们创建一个随机的100x10数组。
In [21]: x = np.random.rand(100,10)
现在,让我们提取数组的前五行,并将它们分配给变量y。
In [22]: y = x[:5, :]
让我们看看y是否是x的视图。
In [23]: np.may_share_memory(x, y)
Out[23]: True
现在让我们修改数组y,看看它如何影响x。 将y的所有元素设置为零:
In [24]: y[:] = 0
In [25]: print(x[:5, :])
Out[25]: [[ 0\. 0\. 0\. 0\. 0\. 0\. 0\. 0\. 0\. 0.]
[ 0\. 0\. 0\. 0\. 0\. 0\. 0\. 0\. 0\. 0.]
[ 0\. 0\. 0\. 0\. 0\. 0\. 0\. 0\. 0\. 0.]
[ 0\. 0\. 0\. 0\. 0\. 0\. 0\. 0\. 0\. 0.]
[ 0\. 0\. 0\. 0\. 0\. 0\. 0\. 0\. 0\. 0.]]
该代码段打印出五行零。 这是因为y只是一个视图,是对x的引用。
接下来,让我们创建一个副本以查看区别。 我们使用前面的方法使用随机函数来创建x数组,但是这次我们使用numpy.empty初始化y数组以首先创建一个空数组,然后将值从x复制到y。 因此,现在y不再是x的视图/参考; 它是一个独立的数组,但具有与x相同的值。 让我们再次使用may_share_memory函数来验证y是x的副本:
In [26]: x = np.random.rand(100,10)
In [27]: y = np.empty([5, 10])
In [28]: y[:] = x[:5, :]
In [29]: np.may_share_memory(x, y)
Out[29]: False
让我们更改y中的值,并检查x的值是否也发生变化:
In [30]: y[:] = 0
In [31]: print(x[:5, :])
您应该看到前面的代码段在初始化x时打印了五行随机数,因此将y更改为0不会影响x。
创建数组
数组可以通过多种方式创建,例如从其他数据结构,通过读取磁盘上的文件或从 Web 创建。 就本章而言,其目的是使我们熟悉 NumPy 数组的核心特性,我们将使用列表或各种 NumPy 函数创建数组。
从列表创建数组
创建数组的最简单方法是使用array函数。 若要创建有效的数组对象,数组函数的参数必须至少满足以下条件之一:
- 它必须是有效的可迭代值或序列,可以嵌套
- 它必须具有返回有效的 numpy 数组的
__array__方法
考虑以下代码段:
In [32]: x = np.array([1, 2, 3])
In [33]: y = np.array(['hello', 'world'])
第一个条件对于 Python 列表和元组始终为true。 从列表或元组创建数组时,输入可能包含不同的(异构)数据类型。 但是,数组函数通常会将所有输入元素转换为数组所需的最合适的数据类型。 例如,如果列表同时包含浮点数和整数,则结果数组将为float类型。 如果它包含一个整数和一个布尔值,则结果数组将由整数组成。 作为练习,请尝试从包含任意数据类型的列表创建数组。
使用range函数是创建整数列表以及数组的最便捷方法之一:
In [34]: x = range(5)
In [35]: y = np.array(x)
NumPy 具有称为arange的便捷函数,该函数结合了range和array函数的功能。 前两行代码与此等效:
In [36]: x = np.arange(5)
对于多维数组,只需嵌套输入列表,如下所示:
In [37]: x = np.array([[1, 2, 3],[4, 5, 6]])
In [38]: x.ndim
Out[38]: 2
In [39]: x.shape
Out[39]: (2, 3)
前面的示例仅说明如何从现有数组或一系列数字创建 NumPy 数组。 接下来,我们将讨论创建具有随机数的数组。
创建随机数组
NumPy 中的random模块提供了各种函数来创建任何数据类型的随机数组。 在整本书中,我们将非常频繁地使用此模块来演示 NumPy 中函数的工作。 random模块大致由以下函数组成:
- 创建随机数组
- 创建数组的随机排列
- 生成具有特定概率分布的数组
我们将在本书中详细介绍所有这些内容。 在本章中,我们将重点介绍random模块中的两个重要函数-rand和random。 这是一个简单的代码段,展示了这两个函数的使用:
In [40]: x = np.random.rand(2, 2, 2)
In [41]: print(x.shape)
Out[41]: (2, 2, 2)
In [42]: shape_tuple = (2, 3, 4)
In [43]: y = np.random.random(shape_tuple)
In [44]: print(y.shape)
Out[44]: (2, 3, 4)
注意传递给两个函数的参数之间的细微差别。 随机函数接受元组作为参数,并创建维数等于元组长度的数组。 各个尺寸的长度等于元组的元素。 另一方面,rand函数采用任意数量的整数参数,并返回一个随机数组,使得其维数等于传递给该函数的整数参数的数量 ,并且各个维度的长度等于整数参数的值。 因此,前面的代码段中的x是三维数组(传递给函数的参数数量),并且x的三个维度中的每个维度的长度均为2(每个参数的值)。 rand是random的便捷函数。 这两个函数可以互换使用,只要传递的参数分别对两个函数均有效即可。
但是,这两个函数的主要缺点是-它们只能创建浮点数组。 如果我们想要一个随机整数数组,则必须将这些函数的输出转换为整数。 但是,这也是一个重大问题,因为 NumPy 的int函数将浮点数截断为最接近 0 的整数(这与floor函数等效)。 因此,将rand或random的输出强制转换为整数将始终返回零数组,因为这两个函数都返回[0, 1)区间内的浮点数。 可以使用randint函数解决此问题,如下所示:
In [45]: LOW, HIGH = 1, 11
In [46]: SIZE = 10
In [47]: x = np.random.randint(LOW, HIGH, size=SIZE)
In [48]: print(x)
Out[48]: [ 6 9 10 7 9 5 8 8 9 3]
randint函数带有三个参数,其中两个是可选的。 第一个参数表示输出值的期望下限,第二个可选参数表示输出值的(专有)上限。 可选的size参数是一个元组,用于确定输出数组的形状。
还有许多其他函数,例如将随机数生成器植入随机子模块中。 有关详细信息,请参考这里。
其他数组
还有一些其他的数组创建函数,例如zeros(),ones(),eye()和其他一些函数(类似于 MATLAB 中的函数)可用于创建 NumPy 数组。 它们的使用非常简单。 数组也可以从文件或从 Web 填充。 我们将在下一章中处理文件 I/O。
数组的数据类型
数据类型是 NumPy 数组的另一个重要内在方面,它的内存布局和索引也是如此。 只需检查数组的dtype属性即可找到 NumPy 数组的数据类型。 尝试以下示例检查不同数组的数据类型:
In [49]: x = np.random.random((10,10))
In [50]: x.dtype
Out[50]: dtype('float64')
In [51]: x = np.array(range(10))
In [52]: x.dtype
Out[52]: dtype('int32')
In [53]: x = np.array(['hello', 'world'])
In [54]: x.dtype
Out [54]: dtype('S5')
许多数组创建函数提供默认的数组数据类型。 例如,np.zeros和np.ones函数默认创建充满浮点数的数组。 但是也可以使它们创建其他数据类型的数组。 考虑以下示例,这些示例演示如何使用 dtype 参数创建任意数据类型的数组。
In [55]: x = np.ones((10, 10), dtype=np.int)
In [56]: x.dtype
Out[56]: dtype('int32')
In [57]: x = np.zeros((10, 10), dtype='|S1')
In [58]: x.dtype
Out[58]: dtype('S1')
有关 NumPy 支持的数据类型的完整列表,请参考这里。
总结
在本章中,我们介绍了 NumPy ndarray对象的一些基础知识。 我们研究了一些创建 NumPy 数组的基本方法。 我们还研究了数组的副本和视图之间的差异,以及它们如何影响使用索引和切片的情况。 我们看到了 NumPy 提供的内存布局之间的细微差别。 现在,我们已经配备了ndarray对象的基本词汇,并且可以开始使用 NumPy 的核心功能。 在下一章中,我们将探索ndarray的更多细节,并使用某些技巧和窍门(通用函数和形状操作)向您展示其中的一些技巧,以使您的 NumPy 脚本加速!
三、使用 NumPy 数组
NumPy 数组的优点在于您可以使用数组索引和切片来快速访问数据或执行计算,同时保持 C 数组的效率。 还支持许多数学运算。 在本章中,我们将深入研究使用 NumPy 数组。 在本章结束之后,您将对使用 NumPy 数组及其大部分功能感到满意。
这是本章将涉及的主题列表:
- NumPy 数组的基本操作和属性
- 通用函数(
ufunc)和辅助函数 - 广播规则和形状操作
- 屏蔽 NumPy 数组
向量化运算
所有 NumPy 操作都是向量化的,您可以将操作应用于整个数组,而不是分别应用于每个元素。 与使用循环相比,这不仅整齐方便,而且还提高了计算性能。 在本节中,我们将体验 NumPy 向量化操作的强大功能。 在开始探索此主题之前,一个值得牢记的关键思想是始终考虑整个数组集而不是每个元素。 这将帮助您享受有关 NumPy 数组及其性能的学习。 让我们从标量和 NumPy 数组之间进行一些简单的计算开始:
In [1]: import numpy as np
In [2]: x = np.array([1, 2, 3, 4])
In [3]: x + 1
Out[3]: array([2, 3, 4, 5])
数组中的所有元素通过1同时添加。 这与 Python 或大多数其他编程语言有很大不同。 NumPy 数组中的元素都具有相同的dtype; 在前面的示例中,这是numpy.int(根据计算机的不同是 32 位或 64 位); 因此,NumPy 可以节省在运行时检查每个元素的类型的时间,这通常是由 Python 完成的。 因此,只需应用以下算术运算:
In [4]: y = np.array([-1, 2, 3, 0])
In [5]: x * y
Out[5]: array([-1, 4, 9, 0])
两个 NumPy 数组逐个元素相乘。 在前面的示例中,两个数组的形状相同,因此此处不应用广播(我们将在后面的部分中解释不同的形状,NumPy 数组操作和广播规则。)数组x中的第一个元素乘以数组y中的第一个元素,依此类推。 这里要注意的重要一点是,两个 NumPy 数组之间的算术运算不是矩阵乘法。 结果仍然返回相同形状的 NumPy 数组。 NumPy 中的矩阵乘法将使用numpy.dot()。 看一下这个例子:
In [6]: np.dot(x, y)
Out[6]: 12
NumPy 还支持两个数组之间的逻辑比较,并且比较也被向量化。 结果返回一个布尔值,并且 NumPy 数组指示两个数组中的哪个元素相等。 如果比较两个不同形状的数组,结果将仅返回一个False,这表明两个数组不同,并且实际上将比较每个元素:
In [7]: x == y
Out[7]: array([False, True, True, False], dtype=bool)
从前面的示例中,我们可以深入了解 NumPy 的元素操作,但是使用它们的好处是什么? 我们怎么知道通过这些 NumPy 操作进行了优化? 我们将使用上一章中介绍的 IPython 中的%timeit函数,向您展示 NumPy 操作和 Python for循环之间的区别:
In [8]: x = np.arange(10000)
In [9]: %timeit x + 1
100000 loops, best of 3: 12.6 µs per loop
In [10]: y = range(10000)
In [11]: %timeit [i + 1 for i in y]
1000 loops, best of 3: 458 µs per loop
x 和y这两个变量的长度相同,并且执行相同的工作,其中包括向数组中的所有元素添加值。 在 NumPy 操作的帮助下,性能比普通的 Python for循环要快得多(我们在这里使用列表推导来编写整洁的代码,这比普通的 Python for循环要快,但是与普通的 Python for循环相比,NumPy 的性能却更好)。 知道这个巨大的区别可以通过用 NumPy 操作替换循环来帮助您加速代码。
正如我们在前面的示例中提到的,性能的提高归因于 NumPy 数组中一致的dtype。 可以帮助您正确使用 NumPy 数组的技巧是在执行任何操作之前始终考虑dtype ,因为您很可能会在大多数编程语言中进行此操作。 下面的示例将为您展示使用相同操作的巨大不同结果,但这是基于不同的dtype数组:
In [12]: x = np.arange(1,9)
In [13]: x.dtype
Out[13]: dtype('int32')
In [14]: x = x / 10.0
In [15]: x
Out[15]: array([ 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8])
In [16]: x.dtype
Out[16]: dtype('float64')
In [17]: y = np.arange(1,9)
In [18]: y /= 10.0
In [19]: y
Out[19]: array([0, 0, 0, 0, 0, 0, 0, 0])
In [20]: y.dtype
Out[20]: dtype('int32')
两个变量x和y完全相同:都是numpy.int32数组,范围从1到8(如果使用 64 位计算机,则可能会得到numpy.int64)并除以float 10.0。 但是,当x除以浮点数时,将使用dtype = numpy.float64创建一个新的 NumPy 数组。 这是一个全新的数组,但是具有相同的变量名x,因此x中的dtype进行了更改。 另一方面,y使用/=符号,该符号始终沿用y数组的dtype值。 因此,当它除以10.0时,不会创建新的数组; 仅更改y元素中的值,但dtype 仍为numpy.int32。 这就是x和y最终具有两个不同数组的原因。 请注意,从 1.10 版本开始,NumPy 不允许将浮点结果强制转换为整数。 因此,必须提高TypeError。
通用函数(ufunc)
NumPy 具有许多通用函数(所谓的ufunc),因此可以利用它们来发挥自己的优势,从而尽可能地减少循环以优化代码。 ufunc在数学,三角函数,汇总统计信息和比较运算方面有很好的覆盖范围。 有关详细的ufunc列表,请参考在线文档。
由于 NumPy 中有大量的ufunc,我们很难在一章中涵盖所有这些函数。 在本节中,我们仅旨在了解如何以及为何应使用 NumPy ufuncs。
基本ufunc入门
大多数ufunc都是一元或二进制的,这意味着它们只能接受一个或两个参数,然后逐元素地或在数学中应用它们。 这称为向量化运算或 NumPy 算术运算,我们已在前面的部分中进行了说明。 以下是一些常见的ufunc:
In [21]: x = np.arange(5,10)
In [22]: np.square(x)
Out[22]: array([25, 36, 49, 64, 81])
ufuncs 中广泛支持数学运算,其中一些基本与numpy.square()或numpy.log()基本相同,而另一些则是高级三角运算,例如numpy.arcsin(),numpy.rad2deg()等。 在这里np.mod()检索除法的余数:
In [23]: y = np.ones(5) * 10
In [24]: np.mod(y, x)
Out[24]: array([ 0., 4., 3., 2., 1.])
一些ufunc具有相似的名称,但它们的功能和行为却大不相同。 首先查看在线文档,以确保获得期望的结果。 这是numpy.minimum() 和numpy.min()的示例:
In [25]: np.minimum(x, 7)
Out[25]: array([5, 6, 7, 7, 7])
In [26]: np.min(x)
Out[26]: 5
如您所见,numpy.minimum()比较两个数组并返回两个数组的最小值。 1 是数组值的形状,其值为 7,因此将其广播到[7, 7, 7, 7, 7]。 我们将在下一节中讨论 NumPy 广播规则。 numpy.min(),仅接受一个必需的参数,并返回数组中最小的元素。
使用更高级的函数
大多数ufunc具有可选参数,以在使用它们时提供更大的灵活性。 以下示例将使用numpy.median()。 这是在numpy.repeat()函数创建的二维数组上使用可选的axis 参数完成的,以重复x数组三次并将其分配给z变量:
In [27]: z = np.repeat(x, 3).reshape(5, 3)
In [28]: z
Out[28]:
array([[5, 5, 5],
[6, 6, 6],
[7, 7, 7],
[8, 8, 8],
[9, 9, 9]])
In [29]: np.median(z)
Out[29]: 7.0
In [30]: np.median(z, axis = 0)
Out[30]: array([ 7., 7., 7.])
In [31]: np.median(z, axis = 1)
Out[31]: array([ 5., 6., 7., 8., 9.])
我们可以不使用axis参数就可以看到numpy.median()函数默认情况下会展平数组并返回中值元素,因此仅返回一个值。 使用axis自变量,如果将其应用于 0,则该操作将基于该列; 因此,我们获得了一个新的 NumPy 数组,其长度为3(z变量中总共有3列)。 虽然axis = 1,它基于行执行操作,所以我们有了一个包含五个元素的新数组。
ufuncs 不仅提供可选参数来调整操作,而且其中许多还具有一些内置方法,从而提供了更大的灵活性。 以下示例使用numpy.add()中的accumulate()累积对所有元素应用add()的结果:
In [32]: np.add.accumulate(x)
Out[32]: array([ 5, 11, 18, 26, 35])
第二个示例将numpy.multiply()上的矩阵外部运算应用于来自两个输入数组的所有元素对。 在此示例中,两个数组来自x。 multiply()的外部产品的最终形状为5x5:
In [33]: np.multiply.outer(x, x)
Out[33]:
array([[25, 30, 35, 40, 45],
[30, 36, 42, 48, 54],
[35, 42, 49, 56, 63],
[40, 48, 56, 64, 72],
[45, 54, 63, 72, 81]])
如果您需要更高级的函数,则可以考虑构建自己的ufunc,这可能需要使用 Python-C API,或者您也可以使用 Numba 模块(向量化装饰器)来实现自定义的ufunc。 在本章中,我们的目标是了解 NumPy ufunc,因此我们将不介绍自定义的ufunc。 有关更多详细信息,请参阅 NumPy 的联机文档,名为编写自己的ufunc或 Numba 文档,创建 Numpy 通用函数。
广播和形状操作
NumPy 操作大部分是按元素进行的,这需要一个操作中的两个数组具有相同的形状。 但是,这并不意味着 NumPy 操作不能采用两个形状不同的数组(请参阅我们在标量中看到的第一个示例)。 NumPy 提供了在较大的数组上广播较小尺寸的数组的灵活性。 但是我们不能将数组广播成几乎任何形状。 它需要遵循某些约束; 我们将在本节中介绍它们。 要记住的一个关键思想是广播涉及在两个不同形状的数组上执行有意义的操作。 但是,不当广播可能会导致内存使用效率低下,从而减慢计算速度。
广播规则
广播的一般规则是确定两个数组是否与尺寸兼容。 需要满足两个条件:
- 两个数组的大小应相等
- 其中之一是 1
如果不满足上述条件,将引发ValueError异常,以指示数组具有不兼容的形状。 现在,我们将通过三个示例来研究广播规则的工作原理:
In [35]: x = np.array([[ 0, 0, 0],
....: [10,10,10],
....: [20,20,20]])
In [36]: y = np.array([1, 2, 3])
In [37]: x + y
Out[37]:
array([[ 1, 2, 3],
[11, 12, 13],
[21, 22, 23]])
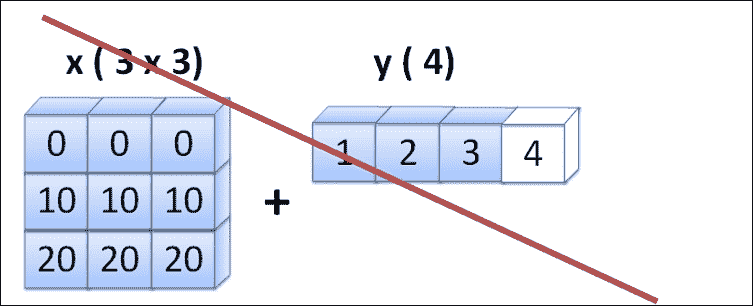
让我们将前面的代码制作成图表,以帮助我们理解广播。 x变量的形状为(3, 3),而y的形状仅为 3。但是在 NumPy 广播中,y的形状转换为1x3; 因此,该规则的第二个条件已得到满足。 通过重复将y广播到x的相同形状。 +操作可以按元素应用。
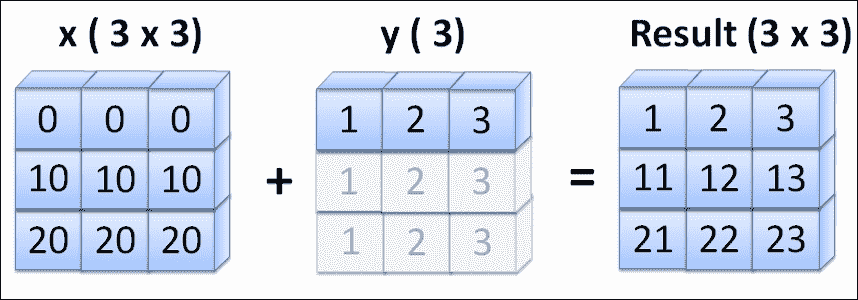
Numpy broadcasting on different shapes of arrays, where x(3,3) + y(3)
接下来,我们将向您展示广播两个数组的结果:
In [38]: x = np.array([[0], [10], [20]])
In [39]: x
Out[39]:
array([[ 0],
[10],
[20]])
In [40]: x + y
Out[40]:
array([[ 1, 2, 3],
[11, 12, 13],
[21, 22, 23]])
前面的示例向您展示x和y的广播方式。 x按列广播,而y按行广播,因为它们的形状在形状上均等于1。 满足第二个广播条件,并且新结果数组是3x3。
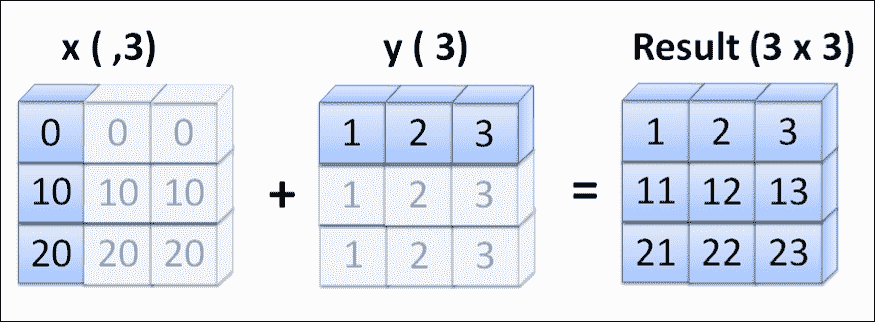
让我们看一下最后一个示例,其中两个数组不能满足广播规则的要求:
In [41]: x = np.array([[ 0, 0, 0],
....: [10,10,10],
....: [20,20,20]])
In [42]: y = np.arange(1,5)
In [43]: x + y
ValueError: operands could not be broadcast together with shapes (3,3) (4)
在第三个示例中,由于x和y在行维度上具有不同的形状,并且它们都不等于1,因此无法执行广播。 因此,不能满足任何广播条件。 NumPy 抛出ValueError,告诉您形状不兼容。
重塑 NumPy 数组
了解广播规则之后,这里的另一个重要概念是重塑 NumPy 数组,尤其是在处理多维数组时。 通常只在一个维度上创建一个 NumPy 数组,然后将其重塑为多维,反之亦然。 这里的一个关键思想是,您可以更改数组的形状,但不应更改元素的数量。 例如,您无法将3xe数组整形为10x1数组。 整形前后,元素的总数(或ndarray内部组织中的所谓数据缓冲区)应保持一致。 或者,您可能需要调整大小,但这是另一回事了。 现在,让我们看一些形状操作:
In [44]: x = np.arange(24)
In [45]: x.shape = 2, 3, -1
In [46]: x
Out[46]:
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
基本的重塑技术会更改numpy.shape属性。 在前面的示例中,我们有一个形状为(24,1)的数组,更改了shape属性后,我们获得了一个相同大小的数组,但是形状已更改为2x3x4组成。 注意, -1的形状是指转移数组的剩余形状尺寸。
In [47]: x = np.arange(1000000)
In [48]: x.shape = 100, 100, 100
In [49]: %timeit x.flatten()
1000 loops, best of 3: 1.14 ms per loop
In [50]: %timeit x.ravel()
1000000 loops, best of 3: 330 ns per loop
前面的示例是将100 x 100 x 100数组整形为一个尺寸; 在这里,我们应用numpy.flatten()和numpy.ravel()这两个函数来折叠数组,同时我们还比较了执行时间。 我们注意到numpy.flatten()和numpy.ravel()之间的速度差异很大,但是它们都比三层 Python 循环快得多。 两个函数在性能上的差异是np.flatten()从原始数组创建副本,而np.ravel()只是更改视图(如果您不记得副本和视图之间的区别,请回到第 2 章, “NumPy ndarray对象”)。
这个例子只是向您展示了 NumPy 提供了许多功能,其中一些可以产生相同的结果。 选择满足您目的的功能,同时为您提供优化的性能。
向量堆叠
重塑会更改一个数组的形状,但是如何通过大小相等的行向量构造二维或多维数组呢? NumPy 为这种称为向量堆叠的解决方案提供了解决方案。 在这里,我们将通过三个示例使用三个不同的栈函数来实现基于不同维度的两个数组的组合:
In [51]: x = np.arange (0, 10, 2)
In [52]: y = np.arange (0, -5, -1)
In [53]: np.vstack([x, y])
Out[53]:
array([[ 0, 2, 4, 6, 8],
[ 0, -1, -2, -3, -4]])
Numpy.vstack()通过垂直堆叠两个输入数组来构造新数组。 新数组是二维的:
In [54]: np.hstack([x, y])
Out[54]: array([ 0, 2, 4, 6, 8, 0, -1, -2, -3, -4])
numpy.hstack()水平合并两个数组时,新数组仍是一维的:
In [55]: np.dstack([x, y])
Out[55]:
array([[[ 0, 0],
[ 2, -1],
[ 4, -2],
[ 6, -3],
[ 8, -4]]])
numpy.dstack()有点不同:它沿三维方向在深度方向上按顺序堆叠数组,因此新数组是三维的。
在下面的代码中,如果您使用numpy.resize()更改数组大小,则您正在放大数组,它将重复自身直到达到新大小; 否则,它将把数组截断为新的大小。 这里要注意的一点是ndarray也具有resize()操作,因此在此示例中,您还可以通过键入x.resize(8)来使用它来更改数组的大小; 但是,您会注意到放大部分填充了零,而不是重复数组本身。 另外,如果您已将数组分配给另一个变量,则无法使用ndarray.resize()。 Numpy.resize()创建一个具有指定形状的新数组,该数组的限制比ndarray.resize()少,并且是在需要时用于更改 NumPy 数组大小的更可取的操作:
In [56]: x = np.arange(3)
In [57]: np.resize(x, (8,))
Out[57]: array([0, 1, 2, 0, 1, 2, 0, 1])
布尔掩码
在 NumPy 中,索引和切片非常方便且功能强大,但是使用布尔掩码,效果会更好! 让我们首先创建一个布尔数组。 请注意,NumPy 中有一种特殊的数组,称为掩码数组。 在这里,我们不讨论它,但是我们还将解释如何使用 NumPy 数组扩展索引和切片:
In [58]: x = np.array([1,3,-1, 5, 7, -1])
In [59]: mask = (x < 0)
In [60]: mask
Out[60]: array([False, False, True, False, False, True], dtype=bool)
从前面的示例中我们可以看到,通过应用<逻辑符号,我们将标量应用于 NumPy 数组,并将新数组命名为mask,它仍被向量化并返回与x形状相同的True/False 布尔值,表示x中的哪个元素符合标准:
In [61]: x [mask] = 0
In [62]: x
Out[62]: array([1, 3, 0, 5, 7, 0])
使用掩码,我们可以在不知道数组索引的情况下访问或替换数组中的任何元素值。 不用说,无需使用for循环即可完成此操作。
以下示例显示了如何对掩码数组求和,其中True代表 1,False 代表 0。我们创建了 50 个随机值,范围从0到1,其中 20 个大于0.5; 但是,对于随机数组,这是非常期望的:
In [69]: x = np.random.random(50)
In [70]: (x > .5).sum()
Out[70]: 20
辅助函数
除了 Python 和其他在线文档中的help()和dir()函数之外,NumPy 还提供了一个辅助函数numpy.lookfor()来帮助您找到所需的正确函数。 参数是一个字符串,可以采用函数名称或任何与之相关的形式。 让我们尝试查找与resize相关的操作的更多信息,我们在前面的部分中进行了介绍:
In [71]: np.lookfor('resize')
Search results for 'resize'
---------------------------
numpy.ma.resize
Return a new masked array with the specified size and shape.
numpy.chararray.resize
Change shape and size of array in-place.
numpy.oldnumeric.ma.resize
The original array's total size can be any size.
numpy.resize
Return a new array with the specified shape.
总结
在本章中,我们介绍了 NumPy 及其ufunc的基本操作。 我们看了 NumPy 操作和 Python 循环之间的巨大差异。 我们还研究了广播的工作原理以及应避免的情况。 我们也试图理解掩蔽的概念。
使用 NumPy 数组的最好方法是尽可能地消除循环,并在 NumPy 中使用 ufuncs。 请记住广播规则,并谨慎使用它们。 将切片和索引与掩码一起使用可提高代码效率。 最重要的是,在使用时要玩得开心。
在接下来的几章中,我们将介绍 NumPy 的核心库,包括日期/时间和文件 I/O,以帮助您扩展 NumPy 的使用体验。
四、NumPy 核心和子模块
在上一章介绍了这么多 NumPy 函数之后,我希望您仍然记得 NumPy 的核心,即ndarray对象。 我们将完成ndarray的最后一个重要属性:步幅,它将为您提供完整的内存布局图。 另外,该向您展示 NumPy 数组不仅可以处理数字,还可以处理各种类型的数据; 我们将讨论记录数组和日期时间数组。 最后,我们将展示如何从文件中读取/写入 NumPy 数组,并开始使用 NumPy 进行一些实际的分析。
本章将涉及的主题是:
- NumPy 数组的核心:内存布局
- 结构数组(记录数组)
- NumPy 数组中的日期时间
- NumPy 数组中的文件 I/O
步幅
步幅是 NumPy 数组中的索引方案,它指示要跳转以查找下一个元素的字节数。 我们都知道 NumPy 的性能改进来自具有固定大小项的同构多维数组对象numpy.ndarray对象。 我们已经讨论了ndarray对象的shape(维度),数据类型和顺序(C 风格的行主要索引数组和 Fortran 风格的列主要数组)。现在让我们仔细看看步幅。
让我们首先创建一个 NumPy 数组并更改其形状以查看步幅的差异。
-
创建一个 NumPy 数组,看一下步幅:
In [1]: import numpy as np In [2]: x = np.arange(8, dtype = np.int8) In [3]: x Out[3]: array([0, 1, 2, 3, 4, 5, 6, 7]) In [4]: x.strides Out[4]: (1,) In [5]: str(x.data) Out[5]: '\x00\x01\x02\x03\x04\x05\x06\x07'创建一维数组
x,其数据类型为 NumPy 整数8,这意味着数组中的每个元素都是 8 位整数(每个 1 字节,总共 8 个字节)。 步幅表示遍历数组时在每个维度上步进的字节元组。 在上一个示例中,它是一个维度,因此我们将元组获得为(1, )。 每个元素与其前一个元素相距 1 个字节。 当我们打印出x.data时,我们可以获得指向数据开头的 Python 缓冲区对象,在示例中从x01到x07。 -
更改形状并查看步幅变化:
In [6]: x.shape = 2, 4 In [7]: x Out[7]: array([[0, 1, 2, 3], [4, 5, 6, 7]], dtype=int8) In [8]: x.strides Out[8]: (4, 1) In [9]: str(x.data) Out[9]: '\x00\x01\x02\x03\x04\x05\x06\x07' In [10]: x.shape = 1,4,2 In [11]: x.strides Out[11]: (8, 2, 1) In [12]: str(x.data) Out[12]: '\x00\x01\x02\x03\x04\x05\x06\x07'现在我们将
x的尺寸更改为 2 乘以 4,然后再次检查步幅。 我们可以看到它变为(4, 1),这意味着第一维中的元素相隔四个字节,并且数组需要跳转四个字节才能找到下一行,但是第二维中的元素仍相隔 1 个字节, 跳一个字节以查找下一列。 让我们再次打印出x.data,我们可以看到数据的内存布局保持不变,但是步幅改变了。 当我们将形状更改为三维时,会发生相同的行为:1 x 4 x 2数组。 (如果我们的数组是按照 Fortran 样式顺序构建的,会怎样?由于形状的变化,步幅将如何变化?尝试创建一个以列为主的数组,并执行相同的操作来检验这一点。) -
所以现在我们知道了什么是步幅,以及它与
ndarray对象的关系,但是步幅如何改善我们的 NumPy 体验? 让我们进行一些步幅操作以更好地理解这一点:两个数组的内容相同,但步幅却有所不同:In [13]: x = np.ones((10000,)) In [14]: y = np.ones((10000 * 100, ))[::100] In [15]: x.shape, y.shape Out[15]: ((10000,), (10000,)) In [16]: x == y Out[16]: array([ True, True, True, ..., True, True, True], dtype=bool) -
我们创建两个 NumPy 数组
x和y并进行比较; 我们可以看到两个数组相等。 它们具有相同的形状,所有元素都是一个,但是实际上这两个数组在内存布局方面是不同的。 让我们简单地使用您在第 2 章, “NumPyndarray对象”中了解的flags属性来检查两个数组的内存布局。In [17]: x.flags Out[17]: C_CONTIGUOUS : True F_CONTIGUOUS : True OWNDATA : True WRITEABLE : True ALIGNED : True UPDATEIFCOPY : False In [18]: y.flags Out[18]: C_CONTIGUOUS : False F_CONTIGUOUS : False OWNDATA : False WRITEABLE : True ALIGNED : True UPDATEIFCOPY : False -
我们可以看到
x数组在 C 和 Fortran 顺序中都是连续的,而y则不是。 让我们检查一下步幅差异:In [19]: x.strides, y.strides Out[19]: ((8,), (800,))数组
x是连续创建的,因此在同一维中,每个元素相隔八个字节(numpy.ones的默认dtype是 64 位浮点数); 但是,y是由每 100 个元素10000 * 100的子集创建的,因此内存布局中的索引架构不是连续的。 -
尽管
x和y具有相同的形状,但y中的每个元素彼此相距 800 个字节。 使用 NumPy 数组x和y时,您可能不会注意到索引的差异,但是内存布局确实会影响性能。 让我们使用 IPython 中的%timeit函数进行检查:In [18]: %timeit x.sum() 100000 loops, best of 3: 13.8 µs per loop In [19]: %timeit y.sum() 10000 loops, best of 3: 25.9 µs per loop
通常,在固定的高速缓存大小的情况下,当步幅大小变大时,命中率(在高速缓存中找到数据的内存访问量的百分比)相对较低,而未命中率(必须访问的内存访问量的百分比) 到内存)将会更高。 缓存命中时间和未命中时间构成了平均数据访问时间。 让我们尝试从缓存的角度再次来看我们的示例。 步幅较小的数组x快于y步幅较大的数组。 性能差异的原因是 CPU 将数据从主存储器分块地拉到其缓存中,步幅越小意味着需要的传输越少。 有关详细信息,请参见下图,其中红线表示 CPU 缓存的大小,蓝框表示包含数据的内存布局。
显然,如果同时需要x和y,则 100 个蓝色框的数据将减少x所需的缓存时间。
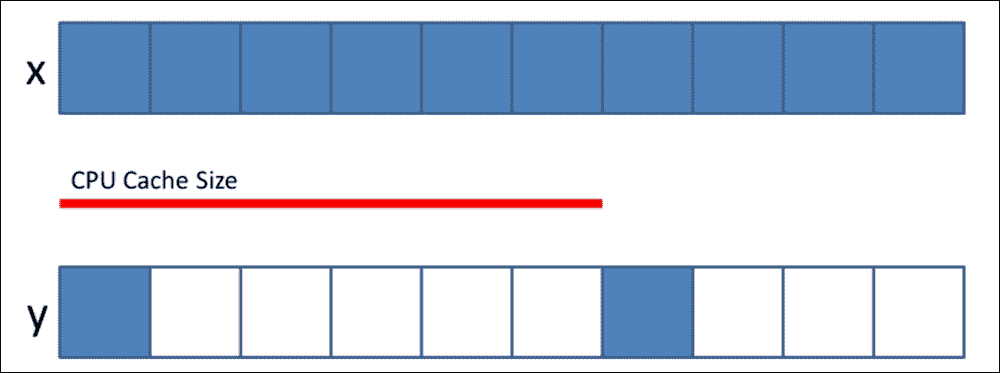
Cache and the x, y array in the memory layout
结构化数组
结构化数组或记录数组在执行计算时很有用,同时您可以将密切相关的数据保持在一起。 例如,当您处理事件数据并且每个事件都包含地理坐标和发生时间时,在计算最终结果时,您可以轻松地找到相关的地理位置和时间点以进行进一步的可视化。 NumPy 还提供了创建记录数组的强大功能,因为一个 NumPy 数组中存在多种数据类型。 但是,在 NumPy 中仍然需要遵守的一个原则是,每个字段中的数据类型(您可以将其视为记录中的列)需要是同质的。 以下是一些简单的示例,向您展示其工作方式:
In [20]: x = np.empty((2,), dtype = ('i4,f4,a10'))
In [21]: x[:] = [(1,0.5, 'NumPy'), (10,-0.5, 'Essential')]
In [22]: x
Out[22]:
array([(1, 0.5, 'NumPy'), (10, -0.5, 'Essential')],
dtype=[('f0', '<i4'), ('f1', '<f4'), ('f2', 'S10')])
在上一个示例中,我们使用numpy.empty()创建了一个一维记录数组,并指定了元素的数据类型-第一个元素是i4(32 位整数,其中i代表有符号整数, 4表示 4 个字节,例如np.int32),第二个元素是 32 位浮点数(f代表float也是 4 个字节),第三个元素是长度小于或等于 10 的字符串。我们按照指定的数据类型顺序将值分配给定义的数组。
您可以看到x的打印输出,该输出现在包含三种不同类型的记录,并且我们还在dtype中获得了默认字段名称:f0,f1和f2。 当然,您可以指定字段名称,如以下示例所示。
这里要注意的一件事是,我们使用了打印输出数据类型-i4和f4前面有一个<,而<代表字节顺序大端(指示内存地址增加顺序):
In [23]: x[0]
Out[23]: (1, 0.5, 'NumPy')
In [24]: x['f2']
Out[24]:
array(['NumPy', 'Essential'], dtype='|S10')
检索数据的方式保持不变,我们使用索引来获取记录,但是此外,我们可以使用字段名称来获取某些字段的值,因此在上一个示例中,我们使用f2来获取字符串字段。 在下面的示例中,我们将创建名为y的x视图,并查看其如何与原始记录数组交互:
In [25]: y = x['f0']
In [26]: y
Out[26]: array([ 1, 10])
In [27]: y[:] = y * 10
In [28]: y
Out[28]: array([ 10, 100])
In [29]: y[:] = y + 0.5
In [30]: y
Out[30]: array([ 10, 100])
In [31]: x
Out[31]:
array([(10, 0.5, 'NumPy'), (100, -0.5, 'Essential')],
dtype=[('f0', '<i4'), ('f1', '<f4'), ('f2', 'S10')])
这里y是x中字段f0的视图。 在记录数组中,NumPy 数组的特征仍然保留。 当您将标量 10 乘以时,它仍然适用于y的整个数组(广播规则),并且始终采用数据类型。 您可以在乘法之后看到,我们在y上添加了0.5,但是由于字段f0的数据类型是 32 位整数,结果仍然是[10, 100]。 另外,y是x中f0的视图,因此它们共享相同的内存块。 当我们在y中进行计算后打印出x时,我们发现x中的值也已更改。
在进一步介绍记录数组之前,让我们先整理一下如何定义记录数组。 最简单的方法如上一个示例所示,在该示例中,我们初始化 NumPy 数组,并使用字符串参数指定字段的数据类型。
NumPy 可以接受多种形式的字符串参数(有关详细信息,请参见这里; 最优选的可以选自以下之一:
| 数据类型 | 表示形式 |
|---|---|
b1 | 字节 |
i1,i2,i4,i8 | 1、2、4 和 8 个字节的带符号整数 |
u1,u2,u4,u8 | 1、2、4 和 8 个字节的无符号整数 |
f2,f4,f8 | 2、4 和 8 个字节的浮点数 |
c8,c16 | 8 和 16 个字节的复数 |
a<n> | 长度为n的定长字符串 |
您也可以在字符串参数前面加上重复的数字或形状,以定义字段的维,但是在记录数组中,它仍仅被视为一个字段。 在下面的示例中,让我们尝试使用形状作为字符串参数的前缀:
In [32]: z = np.ones((2,), dtype = ('3i4, (2,3)f4'))
In [32]: z
Out[32]:
array([([1, 1, 1], [[1.0, 1.0, 1.0], [1.0, 1.0, 1.0]]),
([1, 1, 1], [[1.0, 1.0, 1.0], [1.0, 1.0, 1.0]])],
dtype=[('f0', '<i4', (3,)), ('f1', '<f4', (2, 3))])
在前面的示例中,字段f0是尺寸为3的一维数组,f1是形状为(2, 3)的二维数组。 现在,我们很清楚记录数组的结构以及如何定义它。 您可能想知道默认字段名称是否可以更改为对您的分析有意义的名称? 当然可以! 这是这样的:
In [33]: x.dtype.names
Out[33]: ('f0', 'f1', 'f2')
In [34]: x.dtype.names = ('id', 'value', 'note')
In [35]: x
Out[35]:
array([(10, 0.5, 'NumPy'), (100, -0.5, 'Essential')],
dtype=[('id', '<i4'), ('value', '<f4'), ('note', 'S10')])
通过将新的字段名称分配回dtype对象中的名称属性,我们可以获得自定义的字段名称。 或者,您可以通过使用带有元组的列表或字典来初始化记录数组时执行此操作。 在以下示例中,我们将使用列表和字典来创建两个具有自定义字段名称的相同记录数组:
In [36]: list_ex = np.zeros((2,), dtype = [('id', 'i4'), ('value', 'f4', (2,))])
In [37]: list_ex
Out[37]:
array([(0, [0.0, 0.0]), (0, [0.0, 0.0])],
dtype=[('id', '<i4'), ('value', '<f4', (2,))])
In [38]: dict_ex = np.zeros((2,), dtype = {'names':['id', 'value'], 'formats':['i4', '2f4']})
In [39]: dict_ex
Out[39]:
array([(0, [0.0, 0.0]), (0, [0.0, 0.0])],
dtype=[('id', '<i4'), ('value', '<f4', (2,))])
在列表示例中,我们为每个字段创建一个元组(字段名称,数据类型和形状)。 shape参数是可选的; 您也可以使用数据类型参数指定形状。 使用字典定义字段时,有两个必需的键(names和formats),每个键都有大小相等的值列表。
在继续下一节之前,我们将向您展示如何一次访问记录数组中的多个字段。 以下示例仍使用我们在自定义字段开头创建的数组x:id,value和note:
In [40]: x[['id', 'note']]
Out[40]:
array([(10, 'NumPy'), (100, 'Essential')],
dtype=[('id', '<i4'), ('note', 'S10')])
您可能会发现此示例过于简单; 如果是这样,您可以尝试使用来自维基百科的数据从包含国家名称,人口和排名的真实示例创建一个新的记录数组。 这样会更有趣!
NumPy 中的日期和时间
当您进行时间序列分析时,日期和时间很重要,从简单的事情(如在博物馆中累积每天的访客)到复杂的事情(如对犯罪预测的趋势回归)。 从 NumPy 1.7 开始,NumPy 核心支持日期时间类型(尽管它仍处于试验阶段,并且可能会发生变化)。 为了区别于 Python 中的datetime对象,数据类型称为datetime64。
本节将介绍numpy.datetime64的创建,时间增量算法以及单位与 Python 之间的转换datetime。 让我们使用 ISO 字符串创建一个numpy.datetime64对象:
In [41]: x = np.datetime64('2015-04-01')
In [42]: y = np.datetime64('2015-04')
In [43]: x.dtype, y.dtype
Out[43]: (dtype('<M8[D]'), dtype('<M8[M]'))
x和y都是numpy.datetime64对象,并由 ISO 8601 字符串构造(通用日期格式-有关详细信息,请参见这里。 但是x的输入字符串包含天单位,而y的字符串则没有。 创建 NumPy datetime64时,它将自动从输入字符串的形式中进行选择,因此当我们为x和y都打印出dtype时,我们可以看到x的单位为D。 ]代表几天,而y和单位M代表几个月。 <也是字节序,这里是大端,M8是datetime64的缩写(从np.int64实现)。 numpy.datetime64支持的默认日期单位是年(Y),月(M),周(W)和天(D),而时间单位是小时(h)。 ,分钟(m),秒(s)和毫秒(ms)。
当然,我们在创建数组时可以指定单位,也可以使用numpy.arange()方法创建数组的序列。 请参阅以下示例:
In [44]: y = np.datetime64('2015-04', 'D')
In [45]: y, y.dtype
Out[45]: (numpy.datetime64('2015-04-01'), dtype('<M8[D]'))
In [46]: x = np.arange('2015-01', '2015-04', dtype = 'datetime64[M]')
In [47]: x
Out[47]: array(['2015-01', '2015-02', '2015-03'], dtype='datetime64[M]')
但是,当 ISO 字符串仅包含日期单位时,不允许指定时间单位。 将触发TypeError,因为日期单位和时间单位之间的转换需要选择时区和给定日期的特定时间:
In [48]: y = np.datetime64('2015-04-01', 's')
TypeError: Cannot parse "2015-04-01" as unit 's' using casting rule 'same_kind'
接下来,我们将对两个numpy.datetime64数组进行减法运算,您将看到只要两个数组之间的日期/时间单位是可转换的,广播规则仍然有效。 我们使用先前创建的相同数组x,并为以下示例创建一个新的y:
In [49]: x
Out[49]: array(['2015-01', '2015-02', '2015-03'], dtype='datetime64[M]')
In [50]: y = np.datetime64('2015-01-01')
In [51]: x - y
Out[51]: array([ 0, 31, 59], dtype='timedelta64[D]')
有趣的是,x减去y的结果数组是[0, 31, 59],而不是日期,并且dtype更改为timedelta64[D]。 由于 NumPy 的核心没有物理量系统,因此创建了timedelta64数据类型以补充datetime64。 在上一个示例中,[0, 31, 59]是x中每个元素中从2015-01-01开始的单位,单位是天(D)。 您也可以在datetime64和timedelta64之间进行算术运算,如以下示例所示:
In [52]: np.datetime64('2015') + np.timedelta64(12, 'M')
Out[52]: numpy.datetime64('2016-01')
In [53]: np.timedelta64(1, 'W') / np.timedelta64(1, 'D')
Out[53]: 7.0
在本节的最后部分,我们将讨论numpy.datetime64和 Python datetime之间的转换。 尽管datetime64对象从 NumPy 数组继承了许多特征,但是使用 Python datetime对象(例如date和year属性,isoformat等)仍然有一些好处,反之亦然 。 例如,您可能具有datetime对象的列表,并且可能希望将其转换为用于算术或其他 NumPy 函数的numpy.datetime64。 在下面的示例中,我们将以两种方式将现有的datetime64数组x转换为 Python datetime列表:
In [54]: x
Out[54]: array(['2015-01', '2015-02', '2015-03'], dtype='datetime64[M]')
In [55]: x.tolist()
Out[55]:
[datetime.date(2015, 1, 1),
datetime.date(2015, 2, 1),
datetime.date(2015, 3, 1)]
In [56]: [element.item() for element in x]
Out[56]:
[datetime.date(2015, 1, 1),
datetime.date(2015, 2, 1),
datetime.date(2015, 3, 1)]
我们可以看到带有for循环的numpy.datetime64.tolist()和numpy.datetime64.item()可以实现相同的目标,即将数组转换为 Python datetime对象的列表。 但是不用说,我们都知道哪种方法更适合进行转换(如果您不知道答案,请快速浏览第 3 章,“使用 Numpy 数组”。)另一方面,如果您已经有了 Python datetime的列表,并想将其转换为 NumPy datetime64数组,则只需使用numpy.array()函数。
NumPy 文件 I/O
现在我们可以执行 NumPy 数组计算和操作,并且知道如何构造记录数组,现在是时候进行一些实际的分析了,方法是将文件读入 NumPy 数组并将结果数组输出到文件中以进行进一步的分析。
我们应该谈论先读取文件然后导出文件。 但是现在,我们将逆转此过程,先创建一个记录数组,然后将其输出到 CSV 文件。 我们将导出的 CSV 文件读入 NumPy 记录数组,并将其与原始记录数组进行比较。 我们将要创建的样本数组将包含一个带有连续整数的id字段,一个包含随机浮点数的value字段和一个带有numpy.datetime64['D']的date字段。 本练习将使用您从前面的章节中获得的所有知识。 让我们开始创建记录数组:
In [57]: id = np.arange(1000)
In [58]: value = np.random.random(1000)
In [59]: day = np.random.random_integers(0, 365, 1000) * np.timedelta64(1,'D')
In [60]: date = np.datetime64('2014-01-01') + day
In [61]: rec_array = np.core.records.fromarrays([id, value, date], names='id, value, date', formats='i4, f4, a10')
In [62]: rec_array[:5]
Out[62]:
rec.array([(0, 0.07019801437854767, '2014-07-10'),
(1, 0.4863224923610687, '2014-12-03'),
(2, 0.9525277614593506, '2014-03-11'),
(3, 0.39706873893737793, '2014-01-02'),
(4, 0.8536589741706848, '2014-09-14')],
dtype=[('id', '<i4'), ('value', '<f4'), ('date', 'S10')])
我们首先创建代表所需字段的三个 NumPy 数组:id,value和date。 创建date字段时,我们将numpy.datetime64与大小为1000的随机 NumPy 数组结合使用,以模拟从2014-01-01到2014-12-31范围内的随机日期(365 天)。
然后我们使用numpy.core.records.fromarrays()函数将三个数组合并为一个记录数组,并分配names(字段名称)和formats(数据类型)。 这里要注意的一件事是,记录数组不支持numpy.datetime64对象,因此我们将其作为长度为 10 的日期/时间字符串存储在数组中。
如果您使用的是 Python 3,则会在记录数组(例如b'2014-09-25')的日期/时间字符串的前面找到前缀b。 b在这里代表“字节字面值”,这意味着它仅包含 ASCII 字符(Python 3 中的所有字符串类型均为 Unicode,这是 Python 2 和 3 之间的一大变化)。 因此,在 Python 3 中,将对象(datetime64)转换为字符串将添加前缀以区分普通字符串类型。 但是,这不会影响下一步将记录数组导出到 CSV 文件中的操作:
In [63]: np.savetxt('./record.csv', rec_array, fmt='%i,%.4f,%s')
我们使用numpy.savetxt()函数来处理导出,并使用fmt参数将第一个参数指定为导出文件的位置,数组名称和格式。 我们有三个具有三种不同数据类型的字段,我们想在 CSV 文件的每个字段之间添加,。 如果您更喜欢其他定界符,请在fmt参数中替换逗号。 我们还消除了value字段中的冗余数字,因此我们使用%.4f仅在文件的小数点后指定四位数字。 现在,您可以转到我们在第一个参数中指定的文件位置,以检查 CSV 文件。 在电子表格软件程序中将其打开,您将看到以下内容:
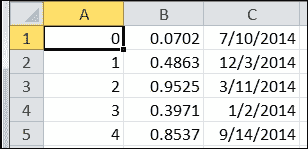
接下来,我们将 CSV 文件读取到记录数组中,并使用value字段生成一个名为mask的掩码字段,该掩码字段表示一个大于或等于 0.75 的值。 然后,我们将新的mask字段追加到记录数组。 让我们先阅读 CSV 文件:
In [64]: read_array = np.genfromtxt('./record.csv', dtype='i4,f4,a10', delimiter=',', skip_header=0)
In [65]: read_array[:5]
Out[65]:
array([(0, 0.07020000368356705, '2014-07-10'),
(1, 0.486299991607666, '2014-12-03'),
(2, 0.9524999856948853, '2014-03-11'),
(3, 0.3971000015735626, '2014-01-02'),
(4, 0.8536999821662903, '2014-09-14')],
dtype=[('f0', '<i4'), ('f1', '<f4'), ('f2', 'S10')])
我们使用numpy.genfromtxt()将文件读入 NumPy 记录数组。 第一个参数仍然是我们要访问的文件位置,dtype参数是可选的。 如果未指定,NumPy 将使用各列的内容分别确定dtype参数。 由于我们清楚地了解数据,因此建议您在每次读取文件时指定一次。
delimiter参数也是可选的,默认情况下,任何连续的空格都用作分隔符。 但是,对于 CSV 文件,我们使用了,。 我们在方法中使用的最后一个可选参数是skip_header。 尽管我们没有在文件中的记录顶部添加字段名称,但是 NumPy 提供了跳过文件开头多行的功能。
除了skip_header之外,numpy.genfromtext()函数还支持 22 种以上的操作参数以微调数组,例如定义缺失值和填充值。 有关更多详细信息,请参阅这里。
现在将数据读到记录数组中,您将发现第二个字段是小数点后四位数以上,这是我们在导出 CSV 时指定的。 这样做的原因是因为我们在读取时使用f4作为其数据类型。NumPy 将填充空数字,但有效的四位数字与文件中的数字相同。 您可能还会注意到我们丢失了字段名,因此让我们指定它:
In [66]: read_array.dtype.names = ('id', 'value', 'date')
本练习的最后一部分是创建一个基于value字段的值大于或等于0.75的掩码变量。 我们将新的掩码数组作为新列附加到read_array中:
In [68]: mask = read_array['value'] >= 0.75
In [69]: from numpy.lib.recfunctions import append_fields
In [70]: read_array = append_fields(read_array, 'mask', data=mask, dtypes='i1')
In [71]: read_array[:5]
Out[71]:
masked_array(data = [(0, 0.07020000368356705, '2014-07-10', 0)
(1, 0.486299991607666, '2014-12-03', 0)
(2, 0.9524999856948853, '2014-03-11', 1)
(3, 0.3971000015735626, '2014-01-02', 0)
dtype = [('id', '<i4'), ('value', '<f4'), ('date', 'S10'), ('mask','i1')])
仅当直接导入numpy.lib.recfunctions且模块中具有append_field()函数时,才能访问它。 追加一个记录数组就像追加一个 NumPy 数组一样简单:第一个参数是基本数组;第二个参数是基本数组。 第二个参数是新字段名称mask以及与之关联的数据; 最后一个参数是数据类型。 由于掩码是布尔数组,因此 NumPy 会自动将掩码应用于记录数组,但是我们仍然可以看到在read_array中添加了一个新字段,掩码的值反映了阈值(>= 0.75) value字段。 这只是向您展示如何将 NumPy 数组与数据文件连接的开始。 现在是时候对您的数据进行一些真实的分析了!
总结
在本章中,我们介绍了ndarray对象的最后一个重要组成部分:步幅。 当您使用不同的方式初始化 NumPy 数组时,我们看到了内存布局和性能上的巨大差异。 我们还了解了记录数组(结构化数组)以及如何在 NumPy 中操纵日期/时间。 最重要的是,我们看到了如何使用 NumPy 读写数据。
NumPy 的强大功能不仅在于其性能或功能,还在于它使分析变得如此容易。 尽可能多地将 NumPy 与您的数据一起使用!
接下来,我们将研究使用 NumPy 进行线性代数和矩阵计算。
五、NumPy 中的线性代数
NumPy 专为数值计算而设计; 在引擎盖下,它仍然是功能强大的ndarray对象,但同时 NumPy 提供了不同类型的对象来解决数学问题。 在本章中,我们将介绍矩阵对象和多项式对象,以帮助您使用非 ndarray 方法解决问题。 同样,NumPy 提供了许多标准的数学算法并支持多维数据。 虽然矩阵无法执行三维数据,但更可取的是使用ndarray对象以及线性代数和多项式的 NumPy 函数(更广泛的 SciPy 库是线性代数的另一个不错的选择,但是 NumPy 是我们关注的重点) 书)。 现在让我们使用 NumPy 进行一些数学运算!
本章将涉及的主题是:
- 矩阵和向量运算
- 分解
- 多项式运算
- 回归和曲线拟合
矩阵类型
对于线性代数,使用矩阵可能更直接。 NumPy 中的矩阵对象继承了ndarray的所有属性和方法,但严格来说是二维的,而ndarray可以是多维的。 使用 NumPy 矩阵的众所周知的优点是它们提供矩阵乘法作为*表示法; 例如,如果x和y是矩阵,则x * y是它们的矩阵乘积。 但是,从 Python 3.5 / NumPy 1.10 开始,新的运算符“
但是,从 Python 3.5 / NumPy 1.10 开始,新的运算符@支持本机矩阵乘法。 因此这是使用ndarray的另一个很好的理由。
但是,矩阵对象仍提供方便的转换,例如逆和共轭转置,而ndarray不提供。 让我们从创建 NumPy 矩阵开始:
In [1]: import numpy as np
In [2]: ndArray = np.arange(9).reshape(3,3)
In [3]: x = np.matrix(ndArray)
In [4]: y = np.mat(np.identity(3))
In [5]: x
Out[5]:
matrix([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])
In [6]: y
Out[6]:
matrix([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
有两种创建或转换为 NumPy 矩阵对象的方法,更优选的方法是使用numpy.mat()或numpy.matrix()。 两种方法都创建矩阵,但是numpy.matrix()创建一个副本,而numpy.mat()仅更改视图; 等效于numpy.matrix(data, copy = False)。 在前面的示例中,我们创建了两个矩阵,两个矩阵均来自ndarray对象(np.identity(3)返回3 x 3的单位数组)。 当然,您可以使用字符串或列表来创建矩阵,例如:np.matrix('0 1 2; 3 4 5; 6 7 8')和np.matrix([[0,1,2],[3,4,5],[6,7,8]])将创建与x相同的矩阵。 在以下示例中,我们将执行一些基本的矩阵运算:
In [7]: x + y
Out[7]:
matrix([[ 1., 1., 2.],
[ 3., 5., 5.],
[ 6., 7., 9.]])
In [8]: x * x
Out[8]:
matrix([[ 15, 18, 21],
[ 42, 54, 66],
[ 69, 90, 111]])
In [9]: np.dot(ndArray, ndArray)
Out[9]:
array([[ 15, 18, 21],
[ 42, 54, 66],
[ 69, 90, 111]])
In [10]: x**3
Out[10]:
matrix([[ 180, 234, 288],
[ 558, 720, 882],
[ 936, 1206, 1476]])
In [11]: z = np.matrix(np.random.random_integers(1, 50, 9).reshape(3,3))
In [12]: z
Out[12]:
matrix([[32, 21, 28],
[ 2, 24, 22],
[32, 20, 22]])
In [13]: z.I
Out[13]:
matrix( [[-0.0237 -0.0264 0.0566]
[-0.178 0.0518 0.1748]
[ 0.1963 -0.0086 -0.1958]])
In [14]: z.H
Out[14]:
matrix([[32 2 32]
[21 24 20]
[28 22 22]])
您可以从前面的示例中看到,当我们使用*表示法时,当您为ndarray使用numpy.dot()时,它会应用矩阵乘法(我们将在下一节中讨论)。 同样,**功率符号以矩阵方式完成。 我们还根据随机函数创建了一个矩阵z,以显示该矩阵何时可逆(非奇异)。 您可以使用numpy.matrix.I获得逆矩阵。 我们还可以使用numpy.matrix.H进行共轭(Hermitian)转置。
现在我们知道了如何创建矩阵对象并执行一些基本操作,是时候进行一些练习了。 让我们尝试求解一个简单的线性方程。 假设我们有一个线性方程A x = b,我们想知道x的值。 可能的解决方案如下:
A-1A x = A-1 b
I x = A-1 b
x = A-1 b
我们通过将A和b的逆数相乘来获得x,所以我们用numpy.matrix来做到这一点:
In [15]: A = np.mat('3 1 4; 1 5 9; 2 6 5')
In [16]: b = np.mat([[1],[2],[3]])
In [17]: x = A.I * b
In [18]: x
Out[18]:
matrix([[ 0.2667],
[ 0.4667],
[-0.0667]])
In [21]: np.allclose(A * x, b)
Out[21]: True
我们获得了x,并使用numpy.allclose()在公差范围内比较了 LHS 和 RHS。 默认的绝对公差为1e-8。 结果返回True,这意味着 LHS 和 RHS 在公差范围内相等,这验证了我们的解决方案。 尽管numpy.matrix()采用普通矩阵形式,但在大多数情况下ndarray足以满足您进行线性代数的需要。 现在我们将简单比较ndarray和matrix的性能:
In [20]: x = np.arange(25000000).reshape(5000,5000)
In [21]: y = np.mat(x)
In [22]: %timeit x.T
10000000 loops, best of 3: 176 ns per loop
In [23]: %timeit y.T
1000000 loops, best of 3: 1.36 µs per loop
此示例显示了转置时ndarray和matrix之间的巨大性能差异。 x和y都具有5,000 x 5,000元素,但是x是二维ndarray,而y将其转换为相同的形状matrix。 即使计算已通过 NumPy 优化,NumPy 矩阵也将始终以矩阵方式进行运算。
虽然默认情况下ndarray会反转尺寸而不是对轴进行置换(矩阵始终对轴进行置换),但这是ndarray中完成的一项巨大的性能改进技巧。 因此,考虑到线性代数的性能,ndarray 特别适用于大型数据集。 仅在必要时使用matrix。 在继续下一节之前,让我们看一下另外两个matrix对象属性,这些属性将matrix转换为基本的ndarray:
In [24]: A.A
Out[24]:
array([[3, 1, 4],
[1, 5, 9],
[2, 6, 5]])
In [25]: A.A1
Out[25]: array([3, 1, 4, 1, 5, 9, 2, 6, 5])
前面的示例使用了我们在线性方程实践中创建的矩阵A。 numpy.matrix.A返回基本的ndarray,numpy.matrix.A1返回一维的ndarray。
NumPy 中的线性代数
在进入 NumPy 的线性代数类之前,我们将在本节的开头介绍五种向量积。 让我们从numpy.dot()产品开始逐一回顾它们:
In [26]: x = np.array([[1, 2], [3, 4]])
In [27]: y = np.array([[10, 20], [30, 40]])
In [28]: np.dot(x, y)
Out[28]:
array([[ 70, 100],
[150, 220]])
numpy.dot()函数执行矩阵乘法,其详细计算如下所示:
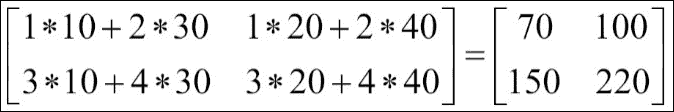
numpy.vdot()处理多维数组的方式与numpy.dot()不同。 它不执行矩阵乘积,而是首先将输入参数展平到一维向量:
In [29]: np.vdot(x, y)
Out[29]: 300
numpy.vdot()的详细计算如下:
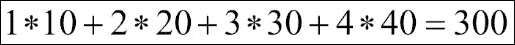
numpy.outer()函数是两个向量的外积。 如果输入数组不是一维的,则它将变平。 假设扁平化的输入向量A的形状为(M, ),扁平化的输入向量B的形状为(N, )。 那么结果形状将是(M, N):
In [100]: np.outer(x,y)
Out[100]:
array([[ 10, 20, 30, 40],
[ 20, 40, 60, 80],
[ 30, 60, 90, 120],
[ 40, 80, 120, 160]])
numpy.outer()的详细计算如下:
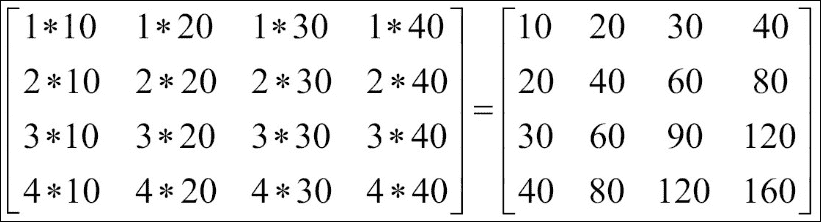
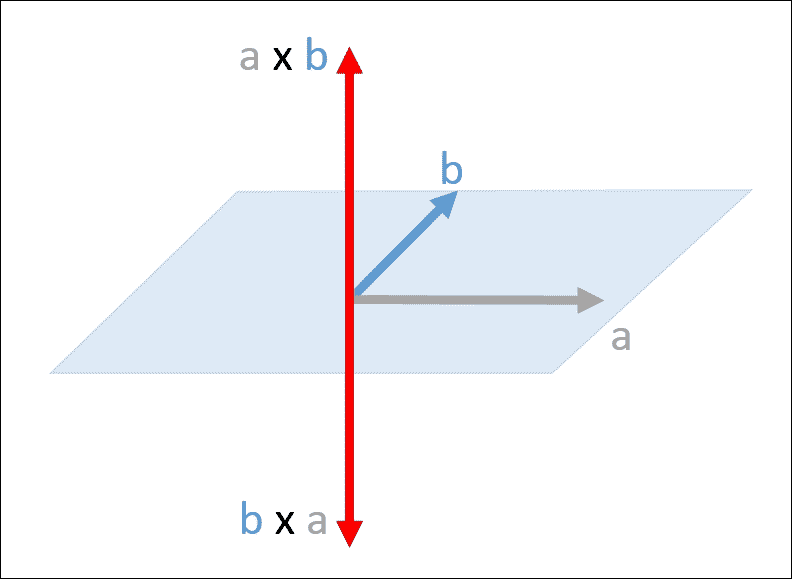
最后一个是numpy.cross()乘积,它是三维空间中两个向量的二进制运算(并且仅适用于向量),其结果是垂直于两个输入数据的向量(a,b)。 如果您不熟悉外部产品,请参考这里。 以下示例显示a和b是向量数组,以及(a,b)和(b,a)的叉积:
In [31]: a = np.array([1,0,0])
In [32]: b = np.array([0,1,0])
In [33]: np.cross(a,b)
Out[33]: array([0, 0, 1])
In [34]: np.cross(b,a)
Out[34]: array([ 0, 0, -1])
下图显示了详细的计算,并且两个向量a与b的叉积由a x b表示:
NumPy 为标准向量例程提供了前面的功能。 现在,我们将讨论本节的关键主题:用于线性代数的numpy.linalg子模块。 将 NumPy ndarray与numpy.linalg结合使用会比numpy.matrix()更好。
注意
如果您希望将 scipy 作为程序的依赖项,则scipy.linalg具有比numpy.linalg更高级的功能,例如矩阵中的三角函数以及更多的分解选择。 但是,NumPy 包含所有基本操作。
在以下示例中,我们将介绍numpy.linalg的其余基本操作,并使用它们来求解矩阵部分中的线性方程:
In [35]: x = np.array([[4,8],[7,9]])
In [36]: np.linalg.det(x)
Out[36]: -20.000000000000007
前面的示例计算方阵的行列式。 当然,我们可以使用numpy.linalg.inv()来计算数组的逆数,就像我们使用numpy.matrix.I一样:
In [37]: np.linalg.inv(x)
Out[37]:
array([[-0.45, 0.4 ],
[ 0.35, -0.2 ]])
In [38]: np.mat(x).I
Out[38]:
matrix([[-0.45, 0.4 ],
[ 0.35, -0.2 ]])
从前面的示例中,我们可以看到numpy.linalg.inv()提供与numpy.matrix.I相同的结果。 唯一的区别是numpy.linalg返回ndarray。 接下来,我们将再次回到线性方程式A x = b,以了解如何使用numpy.linalg.solve()获得与使用矩阵对象相同的结果:
In [39]: x = np.linalg.solve(A,b)
In [40]: x
Out[40]:
matrix([[ 0.2667],
[ 0.4667],
[-0.0667]])
numpy.linalg.solve(A,b)计算x的解,其中第一个输入参数(A)代表系数数组,第二个参数(b)代表坐标或因变量值。 numpy.linalg.solve()函数支持输入数据类型。 在示例中,我们使用矩阵作为输入,因此输出还返回一个矩阵x。 我们也可以使用ndarray 作为输入。
使用 NumPy 进行线性代数运算时,最好仅使用一种数据类型,即ndarray或matrix。 不建议在计算中使用混合类型。 原因之一是减少了不同数据类型之间的转换。 另一个原因是要避免两种类型的计算中的意外错误。 由于ndarray对数据尺寸的限制较少,并且可以执行所有类似矩阵的运算,因此与matrix相比,ndarray与numpy.linalg结合使用是首选的。
分解
numpy.linalg提供了分解,在本节中,我们将介绍两种最常用的分解:奇异值分解(svd)和 QR 因式分解。 让我们首先计算特征值和特征向量。 在我们开始之前,如果您不熟悉特征值和特征向量,可以在这里进行检查。 开始吧:
In [41]: x = np.random.randint(0, 10, 9).reshape(3,3)
In [42]: x
Out[42]:
array([[ 1, 5, 0]
[ 7, 4, 0]
[ 2, 9, 8]])
In [42]: w, v = np.linalg.eig(x)
In [43]: w
Out[43]: array([ 8., 8.6033, -3.6033])
In [44]: v
Out[44]:
array([[ 0., 0.0384, 0.6834]
[ 0., 0.0583, -0.6292]
[ 1., 0.9976, 0.3702]]
)
在前面的示例中,首先我们使用numpy.random.randint ()创建了一个3 x 3的ndarray,然后使用np.linalg.eig()计算了特征值和特征向量。 该函数返回两个元组:第一个元组是特征值,每个元组根据其多重性重复;第二个元组是规范化的特征向量,其中v[: , i]列是与特征值w[i]相对应的特征向量。 在此示例中,我们将元组解压缩为w和v。 如果输入ndarray是复数值,则计算出的特征向量也将是复数类型,如下面的示例所示:
In [45]: y = np.array([[1, 2j],[-3j, 4]])
In [46]: np.linalg.eig(y)
Out[46]:
(array([ -0.3723+0.j, 5.3723+0.j]),
array([[0.8246+0.j , 0.0000+0.416j ],
[-0.0000+0.5658j, 0.9094+0.j ]]))
但是,如果输入ndarray是实数,则计算出的特征值也将是实数; 因此,在计算时,我们应注意舍入错误,如以下示例所示:
In [47]: z = np.array([[1 + 1e-10, -1e-10],[1e-10, 1 - 1e-10]])
In [48]: np.linalg.eig(z)
Out[48]:
(array([ 1., 1.]), array([[0.70710678, 0.707106],
[0.70710678, 0.70710757]]))
ndarrayz是实型(numpy.float64),因此在计算特征值时会自动四舍五入。 从理论上讲,特征值应为1 ± 1e-10,但从第一个np.linalg.eig()可以看出特征值都向上舍入为1。
svd可以认为是特征值的扩展。 我们可以使用numpy.linalg.svd()分解M x N数组,所以让我们从一个简单的例子开始:
In [51]: np.set_printoptions(precision = 4)
In [52]: A = np.array([3,1,4,1,5,9,2,6,5]).reshape(3,3)
In [53]: u, sigma, vh = np.linalg.svd(A)
In [54]: u
Out[54]:
array([[-0.3246, 0.799 , 0.5062],
[-0.7531, 0.1055, -0.6494],
[-0.5723, -0.592 , 0.5675]])
In [55]: vh
Out[55]:
array([[-0.2114, -0.5539, -0.8053],
[ 0.4633, -0.7822, 0.4164],
[ 0.8606, 0.2851, -0.422 ]])
In [56]: sigma
Out[56]: array([ 13.5824, 2.8455, 2.3287])
在此示例中,numpy.linalg.svd()返回了三个元组数组,我们将其解压缩为三个变量:u,sigma和vh,其中u代表A的左奇异向量(AA-1的特征向量),vh是A的右奇异向量(A-1A的特征向量的逆矩阵),sigma是A的非零奇异值(AA-1和A-1A的特征值)。 在该示例中,存在三个特征值,它们按顺序返回。 您可能会对结果感到怀疑,所以让我们做一些数学运算来验证它:
In [57]: diag_sigma = np.diag(sigma)
In [58]: diag_sigma
Out[58]:
array([[ 13.5824, 0\. , 0\. ],
[ 0\. , 2.8455, 0\. ],
[ 0\. , 0\. , 2.3287]])
In [59]: Av = u.dot(diag_sigma).dot(vh)
In [60]: Av
Out[60]:
array([[ 3., 1., 4.],
[ 1., 5., 9.],
[ 2., 6., 5.]])
In [61]: np.allclose(A, Av)
Out[61]: True
输入数组A可以转换为svd中的U ∑ V*,其中∑是奇异向量的值。 但是,从 NumPy 返回的sigma是具有非零值的数组,我们需要将其设为向量,因此在此示例中,形状为(3, 3)。 我们首先使用numpy.diag()制作sigma对角矩阵diag_sigma。 然后我们只需在u,diag_sigma和vh之间执行矩阵乘法,以检查计算结果(Av)是否与原始输入A相同,这意味着我们验证了 svd 结果。
QR 分解(有时称为极坐标分解)可用于任何M x N数组,并将其分解为正交矩阵(Q)和上三角矩阵(R)。 让我们尝试使用它来解决先前的Ax = b问题:
In [62]: b = np.array([1,2,3]).reshape(3,1)
In [63]: q, r = np.linalg.qr(A)
In [64]: x = np.dot(np.linalg.inv(r), np.dot(q.T, b))
In [65]: x
Out[65]:
array([[ 0.2667],
[ 0.4667],
[-0.0667]])
我们使用numpy.linalg.qr()分解A以获得q和r。 因此现在将原始方程式转换为(q * r) x = b。 我们可以使用r和q和b的逆矩阵乘法(点积)获得x。 由于q是一个单位矩阵,因此我们使用了转置而不是逆。 如您所见,结果x与我们使用矩阵和numpy.linalg.solve()时的结果相同; 这是解决线性问题的另一种方法。
注意
通常,三角矩阵逆的计算效率更高,因为您可以创建一个大型数据集并比较不同解决方案之间的性能。
多项式运算
NumPy 还提供了使用多项式的方法,并包括一个名为numpy.polynomial的包,用于创建,操作和拟合多项式。 常见的应用是内插和外推。 在本节中,我们的重点仍然是将ndarray与 NumPy 函数一起使用,而不是使用多项式实例。 (不用担心,我们仍将向您展示多项式类的用法。)
正如我们在矩阵类部分所述,将ndarray与 NumPy 函数结合使用是首选,因为ndarray可以在任何函数中接受,而矩阵和多项式对象则需要转换,尤其是在与其他程序通信时。 它们都提供了方便的属性,但是在大多数情况下,ndarray足够好。
在本节中,我们将介绍如何基于一组根来计算系数,以及如何求解多项式方程,最后我们将求值积分和导数。 让我们从计算多项式的系数开始:
In [66]: root = np.array([1,2,3,4])
In [67]: np.poly(root)
Out[67]: array([ 1, -10, 35, -50, 24])
numpy.poly()返回一阶多项式系数数组,其根是从最高到最低指数的给定数组root。 在此示例中,我们采用根数组[1,2,3,4]并返回多项式,等效于x^4 - 10x^3 + 35x^2 - 50x + 24。
我们需要注意的一件事是输入根数组应该是一维或正方形二维数组,否则会触发ValueError。 当然,我们也可以执行相反的操作:使用numpy.roots()根据系数计算根:
In [68]: np.roots([1,-10,35,-50,24])
Out[68]: array([ 4., 3., 2., 1.])
现在,假设我们有方程式y = x^4 - 10x^3 + 35x^2 - 50x + 24,当x = 5时我们想知道y的值。 我们可以使用numpy.polyval()来计算:
In [69]: np.polyval([1,-10,35,-50,24], 5)
Out[69]: 24
numpy.polyval()具有两个输入参数,第一个是多项式的系数数组,第二个是用于求值给定多项式的特定点值。 我们也可以输入x的序列,结果将返回ndarray,其值对应于给定的x序列。
接下来我们将讨论积分和导数。 我们将继续以x^4 - 10x^3 + 35x^2 - 50x + 24的示例为例:
In [70]: coef = np.array([1,-10,35,-50,24])
In [71]: integral = np.polyint(coef)
In [72]: integral
Out[72]: array([ 0.2 , -2.5 , 11.6667, -25\. , 24\. , 0\. ])
In [73]: np.polyder(integral) == coef
Out[73]: array([ True, True, True, True, True], dtype=bool)
In [74]: np.polyder(coef, 5)
Out[74]: array([], dtype=int32)
在此示例中,我们对整数演算使用numpy.polyint(),结果等于:
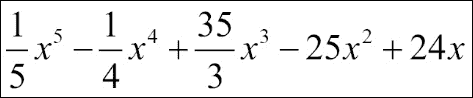
默认积分常数为 0,但我们可以使用输入参数k进行指定。 您可以自己做一些练习,以获得不同的k的积分。
让我们回到前面的示例-完成积分后,我们立即使用numpy.polyder()执行了微积分,并将导数与原始coef数组进行了比较。 我们得到了五个True布尔数组,它们验证了两个数组是否相同。
我们还可以在numpy.polyder()中指定区分的顺序(默认为 1)。 如我们所料,当我们计算四阶多项式的五阶导数时,它将返回一个空数组。
现在,我们将使用多项式类的实例重复这些示例,以查看用法的差异。 使用numpy.polynomial类的第一步是初始化多项式实例。 开始吧:
In [75]: from numpy.polynomial import polynomial
In [76]: p = polynomial.Polynomial(coef)
In [77]: p
Out[77]: Polynomial([ 1., -10., 35., -50., 24.], [-1, 1], [-1, 1])
请注意,在返回的p类型旁边是Polynomial类的实例,并且返回了三部分。 第一部分是多项式的系数。 第二个是domain,它表示多项式中的输入值间隔(默认为[-1, 1])。 第三个是window,它根据多项式将域间隔映射到相应的间隔(默认也是[-1, 1]):
In [78]: p.coef
Out[78]: array([ 1., -10., 35., -50., 24.])
In [79]: p.roots()
Out[79]: array([ 0.25 , 0.3333, 0.5 , 1\. ])
使用Polynomial实例,我们可以简单地调用coef属性以显示系数的ndarray。 roots()方法将显示根。 接下来,我们将求值特定值的多项式5:
In [80]: polynomial.polyval(p, 5)
Out[80]: Polynomial([ 5.], [-1., 1.], [-1., 1.])
集成和派生还使用Polynomial类中的内置函数roots()完成,但函数名称更改为integ()和derive():
In [81]: p.integ()
Out[81]: Polynomial([ 0\. , 1\. , -5\. , 11.6667, -12.5 , 4.8 ], [-1., 1.], [-1., 1.])
In [82]: p.integ().deriv() == p
Out[82]: True
多项式包还提供了特殊的多项式,例如 Chebyshev,Legendre 和 Hermite。 有关这些内容的更多详细信息,请参考这里。
总之,在大多数情况下,ndarray和 NumPy 函数可以解决与多项式有关的问题。 它们也是一种更可取的方式,因为程序中类型之间的转换较少,这意味着较少的潜在问题。 但是,在处理特殊多项式时,我们仍然需要多项式包。 我们几乎完成了数学部分。 在下一节中,我们将讨论线性代数的应用。
应用 – 回归和曲线拟合
由于我们在讨论线性代数的应用,因此我们的经验来自实际案例。 让我们从线性回归开始。 因此,假设我们对一个人的年龄与其睡眠质量之间的关系感到好奇。 我们将使用 2012 年大不列颠睡眠调查在线提供的数据。
有 20,814 人参加了调查,年龄范围从 20 岁以下到 60 岁以上,他们通过 4 到 6 分对他们的睡眠质量进行了评估。
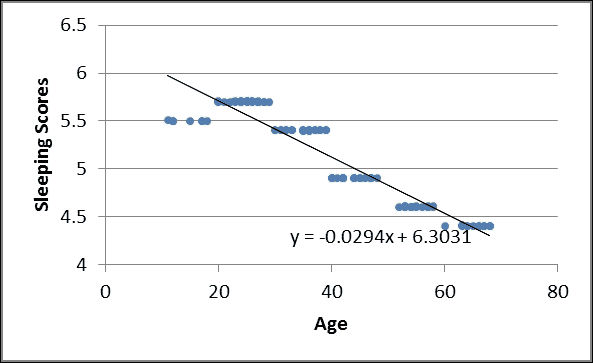
在这种情况下,我们将只使用 100 作为总人口,并模拟年龄和睡眠得分,其分布与调查结果相同。 我们想知道他们的年龄在增长,睡眠质量(分数)增加还是减少? 如您所知,这是一个隐藏的线性回归实践。 一旦我们绘制了年龄和睡眠分数的回归线,通过观察该线的斜率,就可以得出答案。
但是在讨论应该使用哪个 NumPy 函数以及如何使用它之前,让我们首先创建数据集。 根据调查,我们知道 20 岁以下的参与者占 7%,21 岁至 30 岁的参与者占 24%,31 岁至 40 岁的参与者占 21%,60 岁以上的参与者占 21% 。因此,我们首先创建一组列表,代表每个年龄组的人数,并使用numpy.random.randint()模拟我们 100 个人口中的实际年龄,以查看年龄变量。 现在我们知道了每个年龄段的睡眠分数分布,我们称其为scores:这是[5.5, 5.7, 5.4, 4.9, 4.6, 4.4]的列表,[5.5, 5.7, 5.4, 4.9, 4.6, 4.4]是根据年龄段从最小到最大的顺序排列的。 在这里,我们还使用np.random.rand()函数以及均值(来自分数列表)和标准方差(均设置为0.01)来模拟分数分布(当然,如果您有一个好的数据集,则可以使用) ,最好只使用上一章介绍的numpy.genfromtxt()函数):
In [83]: groups = [7, 24, 21, 19, 17, 12]
In [84]: age = np.concatenate([np.random.randint((ind + 1)*10, (ind + 2)*10, group) for ind, group in enumerate(groups)])
In [85]: age
Out[85]:
array(
[11, 15, 12, 17, 17, 18, 12, 26, 29, 24, 28, 25, 27, 25, 26, 24, 23, 27, 26, 24, 27, 20, 28, 20, 22, 21, 23, 25, 27, 24, 25, 35, 39, 33, 35, 30, 32, 32, 36, 38, 31, 35, 38, 31, 37, 36, 39, 30, 36, 33, 36, 37, 45, 41, 44, 48, 45, 40, 44, 42, 47, 46, 47, 42, 42, 42, 44, 40, 40, 47, 47, 57, 56, 53, 53, 57, 54, 55, 53, 52, 54, 57, 53, 58, 58, 54, 57, 55, 64, 67, 60, 63, 68, 65, 66, 63, 67, 64, 68, 66]
)
In [86]: scores = [5.5, 5.7, 5.4, 4.9, 4.6, 4.4]
In [87]: sim_scores = np.concatenate([.01 * np.random.rand(group) + scores[ind] for ind, group in enumerate(groups)] )
In [88]: sim_scores
Out[88]:
array([
5.5089, 5.5015, 5.5024, 5.5 , 5.5033, 5.5019, 5.5012,
5.7068, 5.703 , 5.702 , 5.7002, 5.7084, 5.7004, 5.7036,
5.7055, 5.7024, 5.7099, 5.7009, 5.7013, 5.7093, 5.7076,
5.7029, 5.702 , 5.7067, 5.7007, 5.7004, 5.7 , 5.7017,
5.702 , 5.7031, 5.7087, 5.4079, 5.4082, 5.4083, 5.4025,
5.4008, 5.4069, 5.402 , 5.4071, 5.4059, 5.4037, 5.4004,
5.4024, 5.4058, 5.403 , 5.4041, 5.4075, 5.4062, 5.4014,
5.4089, 5.4003, 5.4058, 4.909 , 4.9062, 4.9097, 4.9014,
4.9097, 4.9023, 4.9 , 4.9002, 4.903 , 4.9062, 4.9026,
4.9094, 4.9099, 4.9071, 4.9058, 4.9067, 4.9005, 4.9016,
4.9093, 4.6041, 4.6031, 4.6016, 4.6021, 4.6079, 4.6046,
4.6055, 4.609 , 4.6052, 4.6005, 4.6017, 4.6091, 4.6073,
4.6029, 4.6012, 4.6062, 4.6098, 4.4014, 4.4043, 4.4013,
4.4091, 4.4087, 4.4087, 4.4027, 4.4017, 4.4067, 4.4003,
4.4021, 4.4061])
现在我们有了年龄和睡眠得分,每个变量都有 100 次事件。 接下来,我们将计算回归线:y = mx + c,其中y代表sleeping_score,而x代表age。 回归线的 NumPy 函数为numpy.linalg.lstsq(),它将系数矩阵和因变量值作为输入。 因此,我们要做的第一件事是将变量年龄打包到一个系数矩阵中,我们称之为AGE:
In [87]: AGE = np.vstack([age, np.ones(len(age))]).T
In [88]: m, c = np.linalg.lstsq(AGE, sim_scores)[0]
In [89]: m
Out[90]: -0.029435313781
In [91]: c
Out[92]: 6.30307651938
现在我们有斜率m和常数c。 我们的回归线是y = -0.0294x + 6.3031,这表明,随着年龄的增长,人的睡眠分数/质量会略有下降,如下图所示:
您可能认为回归线方程看起来很熟悉。 还记得我们在矩阵部分求解的第一个线性方程吗? 是的,您也可以使用numpy.linalg.lstsq()来求解Ax = b方程,实际上这将是本章的第四个解决方案。 自己尝试; 用法与您使用numpy.linalg.solve()时非常相似。
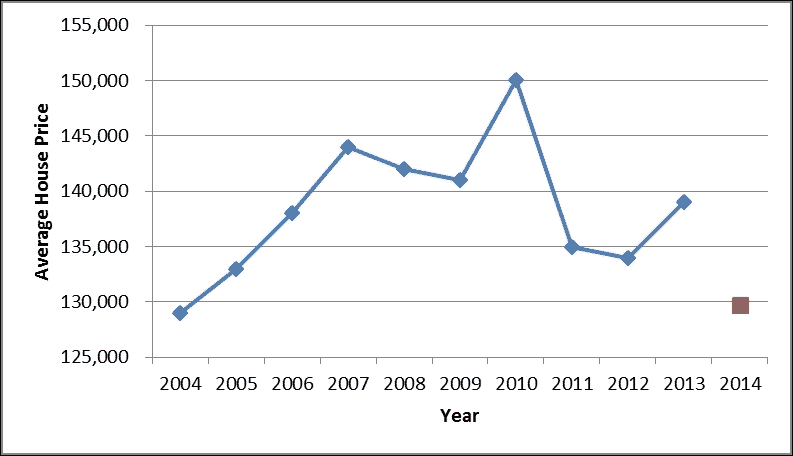
但是,并非每个问题都能简单地通过绘制回归线来回答,例如按年的房价。 它显然不是线性关系,可能是平方或三次关系。 那么我们如何解决这个问题呢? 让我们使用房价指数(国家统计局中的统计数据),然后选择 2004 年至 2013 年。我们将平均房价(英镑)调整为通胀因素; 我们想知道明年的平均价格。
在寻求解决方案之前,让我们首先分析问题。 问题的背后是多项式曲线拟合问题; 我们想找到最适合我们的问题的多项式,但是我们应该为它选择哪个 NumPy 函数? 但是在此之前,让我们创建两个变量:每年的价格price和房屋的年份year:
In [93]: year = np.arange(1,11)
In [94]: price = np.array([129000, 133000, 138000, 144000, 142000, 141000, 150000, 135000, 134000, 139000]).
In [95]: year
Out[95]: array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
现在我们有了年份和价格数据,我们假设它们之间的关系是平方的。 我们的目标是找到多项式:y = ax^2 + bx + c表示关系(一种典型的最小二乘法)。y代表price,x代表year。 这里我们将使用numpy.polyfit()帮助我们找到该多项式的系数:
In [97]: a, b, c = np.polyfit(year, price, 2)
In [98]: a
Out[98]: -549.242424242
In [99]: b
Out[99]: 6641.66666667
In [100]: c
Out[100]: 123116.666667
In [101]: a*11**2 + b*11 + c
Out[101]: 129716.66666666642
我们从numpy.polyfit()获得了多项式的所有系数,它采用三个输入参数:第一个代表自变量:year; 第二个是因变量:price; 最后一个是多项式的阶数,在这种情况下为 2。现在我们只需要使用year = 11(从 2004 年起 11 年),就可以计算出估算价格。 您可以在下图中看到结果:
NumPy 可以从线性代数中获得许多应用,例如插值和外推,但是我们不能在本章中全部介绍它们。 我们希望本章为您使用 NumPy 解决线性或多项式问题提供一个良好的开端。
总结
在本章中,我们介绍了线性代数的矩阵类和多项式类。 我们研究了两个类提供的高级功能,还看到了ndarray在进行基本转置时的性能优势。 我们还介绍了numpy.linalg类,它提供了许多函数来处理ndarray的线性或多项式计算。
在本章中,我们做了很多数学运算,但同时也发现了如何使用 NumPy 帮助我们回答一些现实问题。
在下一章中,我们将了解傅立叶变换及其在 NumPy 中的应用。