题目介绍

该题目取自力扣（LeetCode）面试题 17.04. 消失的数字
链接：消失的数字
该题目主要考察时间复杂度的把握，题目如下：
数组nums包含从0到n的所有整数，但其中缺了一个。请编写代码找出那个缺失的整数。你有办法在O(n)时间内完成吗？
注意：本题相对书上原题稍作改动
示例 1：
输入：[3,0,1]
输出：2
示例 2：
输入：[9,6,4,2,3,5,7,0,1]
输出：8
提示1：
你需要多长时间才能算出缺失数字的最小有效位?
提示2：
要找到缺失的数字中的最小有效位，你其实知道有多少个 0 和 1。例如，如果你看到最小有效位有 3 个 0 和 3 个 1，那么缺失的数字的最小值必定是 1。想想看:在任何 0 和 1 的序列中，你会得到 0，然后是 1，然后又是 0，然后又是 1，以此类推。
提示3：
一旦确定最小有效位是 0(或 1)，就可以排除所有不以 0 作为最小有效位的数。这个问题和前面的有什么不同?

第一种解法：按位异或

这个解法我们先看一张图：
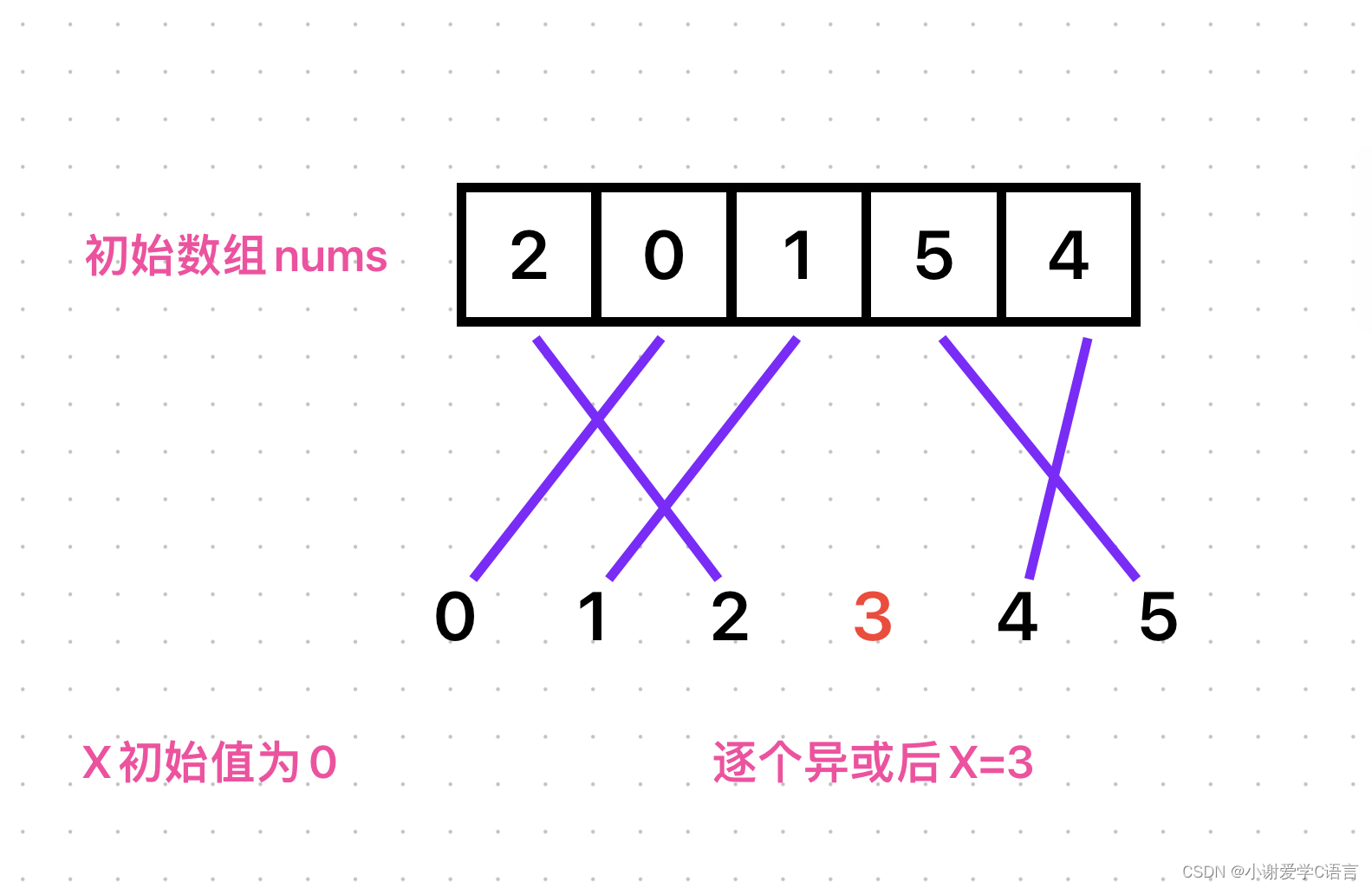
在这里插入图片描述
这种算法的思路主要是先设临时变量x=0，让它与nums数组中的数遍历按位异或，
此时x保存按位异或的值，再与0-n按位异或，最后得到的值就是缺的那个数字。
代码如下：

int missingNumber(int* nums, int numsSize){
    int misNum = 0;
    for(int i = 0; i < numsSize; i++)
    misNum ^= nums[i];
    for(int j = 0; j < numsSize + 1; j++)
    misNum ^= j;
    return misNum;
}

这里主要是利用了按位异或的特性，任何数与他本身按位异或得到的就是0；
那么在这里x按位异或了本身缺失数字的数组nums，再按位异或0-n的数字，
最后剩下的自然就是缺失的数字了。
时间复杂度：O(n)
空间复杂度：O(1)

第二种解法：公式运算

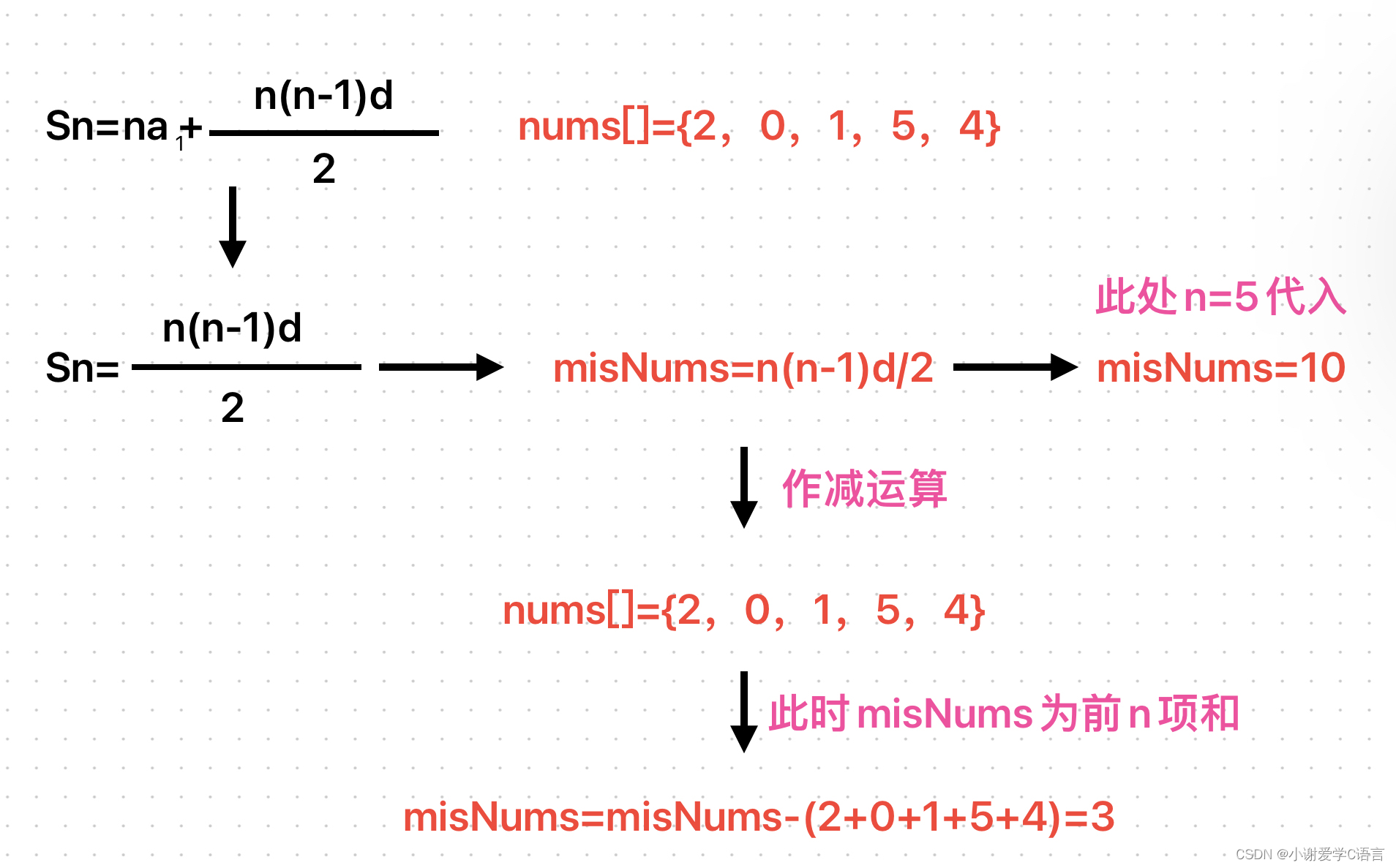
在这里插入图片描述
我们可以先看一张图，我们知道0-n在数学当中是一个自然数数列，那么他的前n项和公式就可以简化为[n(n-1)d]/2,那么这里的思路就是利用数列的前n项和公式先计算出0-n的总和，再建立一个临时变量k,利用一个for循环将nums中的元素逐个相加，最后两数相减得到的自然就是消失的数了。
代码如下：

int missingNumber(int* nums, int numsSize){
    int misNum = (numsSize+1)*numsSize/2;
    int k=0;
    for(int j = 0; j < numsSize; j++)
    k+=nums[j];
    misNum = misNum-k;
    return misNum;
}

时间复杂度：O(n)
空间复杂度：O(1)

第三种解法：临时数组

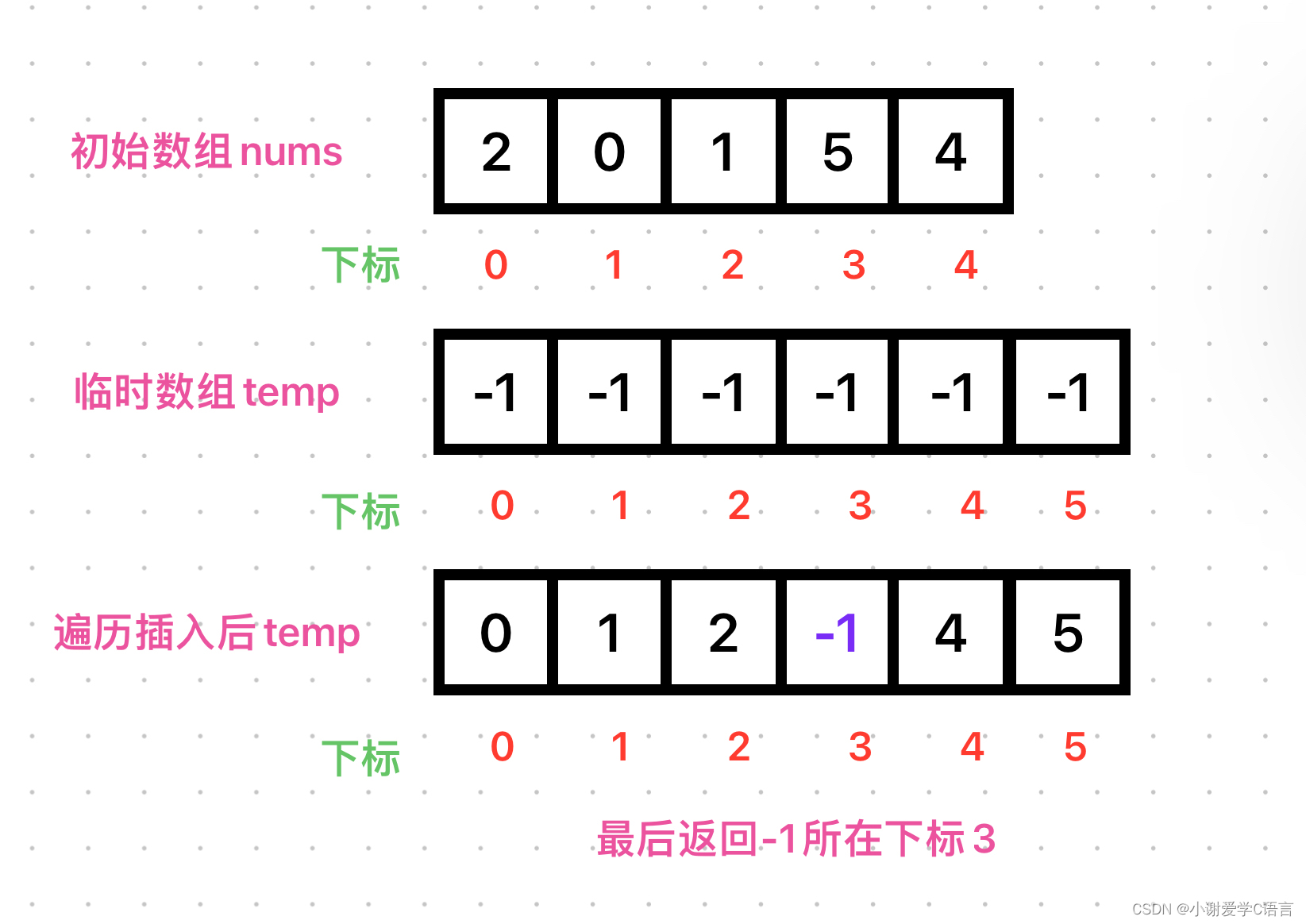
在这里插入图片描述
这里的思路就是用空间换时间，首先我们建立一个临时数组temp，使用malloc函数进行动态内存分配，临时数组temp比初始数组要多一个元素位置，然后将每一个位置都赋值为-1（因为nums是0-n，只有负数不会重复，想给负多少都可以），再将nums中的元素利用for循环逐个找到temp中对应下标进行赋值，最后剩下的-1所对应的下标即为消失的数字，最后再用for循环遍历数组，找到值为-1的元素下标，返回下标即为消失的数字（别忘记把temp的空间释放，否则会造成内存泄露的问题）。
代码如下：

int missingNumber(int* nums, int numsSize)
{
    int* temp = (int*)malloc(sizeof(int) * (numsSize + 1));
    if (temp == NULL)
    {
        perror("missingNumber::malloc");
        return 0;
    }
    int i = 0;
    for (i = 0; i < numsSize + 1; i++)
    {
        *(temp+i) = -1;
    }
    for (i = 0; i < numsSize; i++)
    {
        temp[*nums] = *nums;
        nums++;
    }
    for (i = 0; i < numsSize + 1; i++)
    {
        if (*(temp + i) == -1)
        {
            free(temp);
            temp == NULL;
            return i;
        }
    }
    return ;
}

时间复杂度：O(n)
空间复杂度：O(n)

第四种解法：相加再相减

这种方法和公式法类似，这个的好处在于不用怎么动脑子，简单粗暴，先设立临时变量misNum,让misNum和0-n的值逐个相加，再利用一个for循环对nums数组进行遍历相减，最后得到的misNum的值即为消失的数。
代码如下：

int missingNumber(int* nums, int numsSize){
    int misNum = 0;
    for(int j = 0; j < numsSize + 1; j++)
    misNum += j;
    for(int i = 0; i < numsSize; i++)
    misNum -= nums[i];
    return misNum;
}

时间复杂度：O(n)
空间复杂度：O(1)

第五种解法：快排加二分查找

这种方法需要学到后序的数据结构中快速排序的知识，如果尚未学习，可以只参照前面4种解法，后续我还会出单独的板块介绍各类排序。

快速排序使用了“分治法”和“递归”技巧，将一个数组分成两个子数组，其中一个子数组的所有元素都小于另一个子数组的所有元素，并按照同样的方式对这两个子数组进行排序。快速排序中的关键步骤是“Partition（划分）”函数，它选择一个pivot（枢轴），然后通过交换元素的方式，将数组分成两个部分。

在该代码的“Partition”函数中，我们选择第一个元素为枢轴（pivot），然后使用两个指针low和high，从数组的两端开始遍历数组，交换两个指针所指的元素，以保证左侧的元素小于pivot，右侧的元素大于pivot。最后，将枢轴元素放在正确的位置上。

在“QuickSort”函数中，我们使用“Partition”函数将数组划分为两个子数组，然后对这两个子数组递归地进行排序。

在“missingNumber”函数中，我们先对输入数组进行排序，然后使用二分查找的技巧来找到缺失的数字。具体来说，我们定义左侧指针为0，右侧指针为数组的长度，然后计算中间位置mid，如果mid处的元素等于mid，则说明缺失的数字在mid的右侧，我们将左指针移到mid的右侧，否则缺失的数字在mid的左侧，我们将右指针移到mid的左侧。最终，左侧指针指向的位置就是消失的数字。
代码如下：

 int Partition(int *A, int low, int high){
    int pivot=A[low];
    while(low<high){
        while(low<high && A[high]>=pivot) high--;
        A[low]=A[high];
        while(low<high && A[low]<=pivot) low++;
        A[high]=A[low];
    }
    A[low]=pivot;
    return low;
 }

 void QuickSort(int *A, int low, int high){
    if(low<high){
        int PartitionPos = Partition(A,low, high);
        QuickSort(A,low,PartitionPos-1);
        QuickSort(A,PartitionPos+1, high);
    }

 }

int missingNumber(int* nums, int numsSize){
    QuickSort(nums, 0, numsSize-1);
    int left=0, right=numsSize;
    while(left<right){
        int mid=left+(right-left)/2;
        if(nums[mid]==mid){
            left=mid+1;
        }
        else{
            right=mid;
        }
    }
    return left;

}