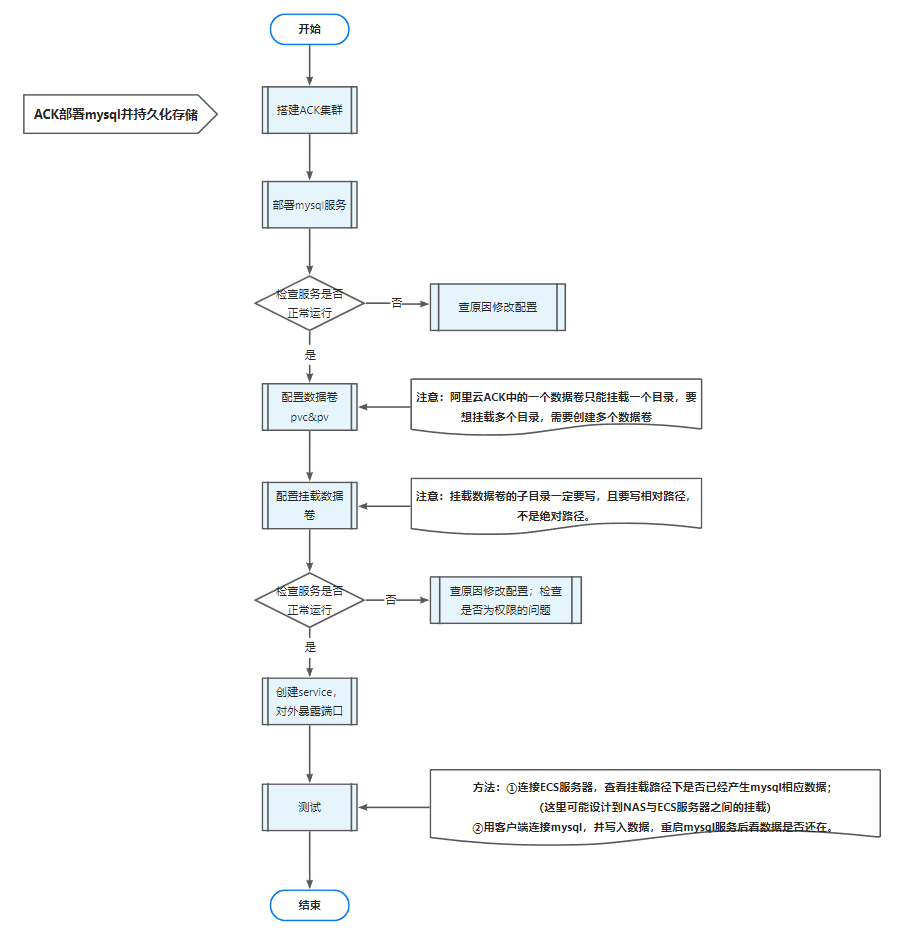
二分法
二分查找:找目标值位置
二分法是一种适用于特殊场景下的分治算法。
这里的特殊场景指的是,二分法需要作用在一个具有单调性的区间内。
比如,我们熟知的二分查找,就是一种二分法的具体实现,二分查找必须在一个升序或者降序的数组内,才能正确地找到目标值。
下面举个例子,演示下二分查找的过程:
有升序数组 arr = [1, 3, 5, 7, 9, 11, 13],请找出元素3在数组中的索引位置?
我们首先要为二分查找定义一个初始的查找范围[L, R],通常情况下 L = 0, R = arr.length-1,如下图所示,即两个指针分别指向数组的首尾:

这里其实不好看单调性,我们将其转化为单调函数f(x) = 2x + 1,其中x是元素索引位置,f(x)是元素值,目标值为target

有了L,R后,我们就需要求出其中间位置mid = (L + R)/ 2

然后比较f(mid)和target的大小:
- 若 f(mid) > target,那么当前f(x)是单调递增的,因此target的位置 < mid
- 若 f(mid) < target,那么当前f(x)是单调递增的,因此target的位置 > mid
- 若 f(mid) == target,那么当前f(x)是单调递增的,因此target的位置 == mid
我们根据f(mid)和target的大小,就能知道target的索引位置和mid的关系,那么知道了target索引位置和mid的关系,有什么用呢?
答案是,可以缩小二分查找的范围。
- 若 f(mid) > target,那么当前f(x)是单调递增的,因此target的位置 < mid,那么下次二分查找的右边界R就可以左移到mid-1
- 若 f(mid) < target,那么当前f(x)是单调递增的,因此target的位置 > mid,那么下次二分查找的左边界就可以右移到mid+1
比如本题target=3,此时f(mid) = 7,则f(mid) > target,由于f(x)是单调递增的,可得target的位置 < mid,因此下次二分查找的右边界R就可以左移到mid-1
即如下图所示

这里需要思考的是,为什么R不是左移到mid(即索引3),而是左移到了mid-1(即索引2)?
其实这个原因很简单,我们已经知道了f(mid) > target了,即说明mid位置不可能是所求目标值target的位置,因此我们下次二分查找的区间没有必要包含此时的mid位置。
进入新的二分区间L,R后,我们继续取中间位置 mid = (L + R) / 2

此时可以发现,f(mid) == target,那么此时mid位置就是目标值target的位置,可以直接返回。
如果用代码实现上面二分查找逻辑的话,如下:
Java
public class Main {
public static void main(String[] args) {
// int[] arr = {1, 3, 5, 7, 9, 11, 13};
int[] arr = {13, 11, 9, 7, 5, 3, 1};
int target = 3;
System.out.println(binarySearch(arr, target));
}
// 二分查找
public static int binarySearch(int[] arr, int target) {
int l = 0;
int r = arr.length - 1;
// 是否是单调递增的数组
boolean isIncremental = arr[l] < arr[r];
while (l <= r) {
int mid = (l + r) / 2;
int midVal = arr[mid];
if (midVal > target) {
if (isIncremental) r = mid - 1;
else l = mid + 1;
} else if (midVal < target) {
if (isIncremental) l = mid + 1;
else r = mid - 1;
} else {
return mid;
}
}
return -1;
}
}
JS
// 二分查找
function binarySearch(arr, target) {
let l = 0;
let r = arr.length - 1;
// 单调性确认
const isIncremental = arr[l] < arr[r];
while (l <= r) {
const mid = Math.floor((l + r) / 2);
const midVal = arr[mid];
if (midVal > target) {
isIncremental ? (r = mid - 1) : (l = mid + 1);
} else if (midVal < target) {
isIncremental ? (l = mid + 1) : (r = mid - 1);
} else {
return mid;
}
}
return -1;
}
// 测试
const target = 3;
const arr = [1, 3, 5, 7, 9, 11, 13];
console.log(binarySearch(arr, target));
arr.reverse();
console.log(binarySearch(arr, target));
Python
# 二分查找
def binarySearch(arr, target):
l = 0
r = len(arr) - 1
# 单调性确认
isIncremental = arr[l] < arr[r]
while l <= r:
mid = (l + r) // 2
midVal = arr[mid]
if midVal > target:
if isIncremental:
r = mid - 1
else:
l = mid + 1
elif midVal < target:
if isIncremental:
l = mid + 1
else:
r = mid - 1
else:
return mid
return -1
# 测试
arr = [1, 3, 5, 7, 9, 11, 13]
target = 3
print(binarySearch(arr, target))
arr.reverse()
print(binarySearch(arr, target))
二分查找:找目标值有序插入位置
上面算法实现中,我们可以发现,如果找不到目标值的位置,算法直接返回了-1,即表示数组中没有目标值元素。
但是有时候,我们会有一个需求,那就是如果数组中不存在目标值,那么就返回目标值在数组中的有序插入位置。
什么意思呢?
比如,arr = [1, 3, 5, 7, 9, 11, 13],现在目标值是4,那么我们应该将目标值插入到数组哪个位置,才能保证数组有序性不被破坏呢?
答案很明显,目标值4的插入位置是索引2。即插入后,arr = [1, 3, 4, 5, 7, 9, 11, 13]
下面是基于之前的二分查找逻辑,找目标值4位置的演示过程



最后L == R时,还可以进入while循环,此时mid == L == R,但是依旧 f(mid) > target,此时由于单调递增,因此target的位置应该在mid的左侧,即R = mid - 1

此时R < L,退出循环。
我们可以发现此时L指向的位置就是target的插入位置。
大家有兴趣的话,可以继续尝试下单调递减数组,最终结论是一样的。
因此,其实前面二分查找算法如果最终找不到目标值位置,那么最后L指针的位置其实就是目标值target的有序插入位置。
那么我们该如何返回这个有序插入位置呢?
根据Java的Arrays.binarySearch设计,有序插入位置返回为 -L-1。
比如上面例子中L=2,那么binarySearch就要返回-3。
为什么要这么设计呢?
如果数组中可以找到目标值,那么目标值索引可能是0~arr.length-1中任意一个。
因此,数组中如果找不到目标值,那么此时我们不能直接目标值的有序插入位置,这会产生冲突,即搞不清楚binarySearch返回值是目标值的索引位置,还是有序插入位置。
而为了避免冲突,有序插入位置都设计为负数。即从-1开始。比如有序插入位置L=0,那么binarySearch就返回-1,即-L-1。
因此,前面binarySearch方法的实现,可以新增一个返回有序插入位置的功能:
Java
public class Main {
public static void main(String[] args) {
int[] arr = {1, 3, 5, 7, 9, 11, 13};
int target = 4;
int idx = binarySearch(arr, target);
if (idx < 0) {
System.out.println(-idx - 1);
}
}
// 二分查找
public static int binarySearch(int[] arr, int target) {
int l = 0;
int r = arr.length - 1;
// 是否是单调递增的数组
boolean isIncremental = arr[l] < arr[r];
while (l <= r) {
int mid = (l + r) / 2;
int midVal = arr[mid];
if (midVal > target) {
if (isIncremental) r = mid - 1;
else l = mid + 1;
} else if (midVal < target) {
if (isIncremental) l = mid + 1;
else r = mid - 1;
} else {
return mid;
}
}
// 若查找目标值,则返回目标值在数组中的有序插入位置l,为了避免产生冲突,返回-l-1
return -l - 1;
}
}
JS
// 二分查找
function binarySearch(arr, target) {
let l = 0;
let r = arr.length - 1;
// 单调性确认
const isIncremental = arr[l] < arr[r];
while (l <= r) {
const mid = Math.floor((l + r) / 2);
const midVal = arr[mid];
if (midVal > target) {
isIncremental ? (r = mid - 1) : (l = mid + 1);
} else if (midVal < target) {
isIncremental ? (l = mid + 1) : (r = mid - 1);
} else {
return mid;
}
}
// 若查找目标值,则返回目标值在数组中的有序插入位置l,为了避免产生冲突,返回-l-1
return -l - 1;
}
// 测试
const target = 4;
const arr = [1, 3, 5, 7, 9, 11, 13];
const idx = binarySearch(arr, target);
if (idx < 0) {
console.log(-idx - 1);
}
Python
# 二分查找
def binarySearch(arr, target):
l = 0
r = len(arr) - 1
# 单调性确认
isIncremental = arr[l] < arr[r]
while l <= r:
mid = (l + r) // 2
midVal = arr[mid]
if midVal > target:
if isIncremental:
r = mid - 1
else:
l = mid + 1
elif midVal < target:
if isIncremental:
l = mid + 1
else:
r = mid - 1
else:
return mid
# 若查找目标值,则返回目标值在数组中的有序插入位置l,为了避免产生冲突,返回-l-1
return -l-1
# 测试
arr = [1, 3, 5, 7, 9, 11, 13]
target = 4
idx = binarySearch(arr, target)
if idx < 0:
print(-idx-1)三分法
三分法的应用场景
通过前面对二分法的研究,我们可以发现二分法必须在一个单调性区间内工作。
那么如果某区间不是一个单调性的,
比如有区间[l, r],其中[l, x]满足单调递增,而[x, r]满足单调递减, 即一个凸函数,即如下图所示

或者,有区间[l, r],其中[l, x]是单调递减的,而[x, r]是单调递增的,即一个凹函数,如下图所示

此时二分法可以找到极值点吗?
- 极值点就是凸函数的最大值点,或者凹函数的最小值点。
答案是不可以的,因为二分法只能在单调区间内工作,而极值点处于一个非单调区间内,因此二分法无法正确找到凹凸函数的极值点。
此时我们就需要借助三分法来实现凹凸函数找极值点。
三分法找极值点有两种策略:
- 三等份
- 近似三等份
三等份
前面研究二分法时,我们是找L,R的中间位置mid,并比较f(mid)和target的大小,来确定target的位置在mid的左侧还是右侧,或者就是mid本身。
而对于凹凸函数而言,我们需要找到L,R区间的三等份点。
什么是三等份点?即可以将[L, R]区间均分为三等份的两个点,
比如下图mL,mR就是三等份点

[L,R]区间被mL和mR点均分为了L~mL,mL~mR,mR~R三个等份区间。
如果 f(mL) <= f(mR),那么对于凸函数而言,极值点必然在mL的右侧,但是极值点和mR的位置关系是不确定的,如下图所示


反之,如果 f(mL) >= f(mR),那么对于凸函数而言,极值点必然在mR的左侧,但是极值点和mL的位置关系不确定。
因此,对于凸函数而言:
如果 f(mL) <= f(mR),那么可以确定极值点位置在mL的右侧,即此时缩小三分区间时,可以将L右移到mL位置。
如果 f(mL) >= f(mR),那么可以确定极值点位置在mR的左侧,即此时缩小三分区间时,可以将R左移到mR位置。
当新的[L, R]区间确认后,则可以继续进行三等份点确认,然后重复上面逻辑。
那么何时结束呢?
三分法和二分法的区别在于,三分法的L < R总是成立,为什么呢?
因为上面缩小区间时,L是直接移动到mL位置,或者R直接移动到mR位置。大家可以看下这个视频,从04:19开始
【【4K算法详解】【二分与三分】从二分法到牛顿法,领着你的思维带你观望方程求解与数值优化算法】
此时就需要一个精度,即当L和R之间的距离小于等于某个精度时,就可以认为当前L或R就是所求的极值点位置。这里的精度通常用eps表示。
我们用代码代码实现三分法找极值
Java
public class Main {
public static void main(String[] args) {
// 测试
System.out.println(trichotomy(-100, 10));
}
// 凸函数 f(x) = -x^2
public static double f(double x) {
return -x * x;
}
// 求凸函数极值
public static double trichotomy(double l, double r) {
// 精度
double eps = 0.00001;
while (r - l >= eps) {
double thridPart = (r - l) / 3;
// 靠左三等份点
double ml = l + thridPart;
// 靠右三等份点
double mr = r - thridPart;
// 凸函数l,r移动逻辑
if (f(ml) < f(mr)) {
l = ml;
} else {
r = mr;
}
}
return l;
}
}
JS
// 凸函数 f(x) = -x^2
function f(x) {
return -(x ** 2);
}
// 求凸函数极值
function trichotomy(l, r) {
// 精度
const eps = 0.00001;
while (r - l >= eps) {
const thridPart = (r - l) / 3;
// 靠左三等份点
const ml = l + thridPart;
// 靠右三等份点
const mr = r - thridPart;
// 凸函数l,r移动逻辑
if (f(ml) < f(mr)) {
l = ml;
} else {
r = mr;
}
}
return l;
}
// 测试
console.log(trichotomy(-100, 10));
Python
# 凸函数 f(x) = -x^2
def f(x):
return -(x ** 2)
# 求凸函数极值
def trichotomy(l, r):
# 精度
eps = 0.00001
while r - l >= eps:
thridPart = (r - l) / 3
# 靠左三等份点
ml = l + thridPart
# 靠右三等份点
mr = r - thridPart
# 凸函数l,r移动逻辑
if f(ml) < f(mr):
l = ml
else:
r = mr
return l
# 测试
print(trichotomy(-100, 10))
近似三等份
上面算法是将[L,R]区间均分为三等份,而更优的策略是直接找[L,R]的中间点mid,然后只根据mid点就能确定极值点的位置。
怎么办到的呢?如下图所示mid是L,R的中间点。

此时我们可以找一个很小的精度accuracy,然后比较两个位置点的关系:
- mid + accuracy
- mid - accuracy
对于凸函数而言:
- 如果 f(mid - accuracy) < f(mid + accuracy),那么说明mid点处于凸函数的上升区间中,即极值点位置在mid的右侧,下次缩小区间时,应该让L = mid
- 如果 f(mid - accuracy) > f(mid + accuracy),那么说明mid点处于凸函数的下降区间中,即极值点位置在mid的左侧,下次缩小区间时,应该让R = mid
实现代码如下
Java
public class Main {
public static void main(String[] args) {
// 测试
System.out.println(trichotomy(-100, 10));
}
// 凸函数 f(x) = -x^2
public static double f(double x) {
return -x * x;
}
// 求凸函数极值
public static double trichotomy(double l, double r) {
// 精度
double eps = 0.00001;
double accuracy = 0.000000001;
while (r - l >= eps) {
double mid = (r + l) / 2;
// 凸函数l,r移动逻辑
if (f(mid - accuracy) < f(mid + accuracy)) {
l = mid;
} else {
r = mid;
}
}
return l;
}
}
JS
// 凸函数 f(x) = -x^2
function f(x) {
return -(x ** 2);
}
// 求凸函数极值
function trichotomy(l, r) {
// 精度
const eps = 0.00001;
const acc = 0.0000000001;
while (r - l >= eps) {
const mid = (r + l) / 2;
if (f(mid - acc) < f(mid + acc)) {
l = mid;
} else {
r = mid;
}
}
return l;
}
// 测试
console.log(trichotomy(-100, 10));
Python
# 凸函数 f(x) = -x^2
def f(x):
return -(x ** 2)
# 求凸函数极值
def trichotomy(l, r):
# 精度
eps = 0.00001
acc = 0.0000000001
while r - l >= eps:
mid = (r + l) / 2
if f(mid - acc) < f(mid + acc):
l = mid
else:
r = mid
return l
# 测试
print(trichotomy(-100, 10))
洛谷P3328 【模板】三分法
题目链接
P3382 【模板】三分法 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
三等份求解
Java
import java.util.Scanner;
public class Main {
static int n;
static double l;
static double r;
static double[] a;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
l = sc.nextDouble();
r = sc.nextDouble();
a = new double[n + 1];
for (int i = 0; i <= n; i++) {
a[i] = sc.nextDouble();
}
System.out.println(getResult());
}
public static double getResult() {
while (r - l >= 0.000001) {
double ml = l + (r - l) / 3.0;
double mr = r - (r - l) / 3.0;
if (f(ml) < f(mr)) l = ml;
else r = mr;
}
return l;
}
public static double f(double x) {
double ans = 0;
for (int i = n; i >= 0; i--) {
ans += Math.pow(x, i) * a[n - i];
}
return ans;
}
}JS
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
let n, l, r, a;
rl.on("line", (line) => {
lines.push(line);
if (lines.length == 2) {
[n, l, r] = lines[0].split(" ").map(Number);
a = lines[1].split(" ").map(Number);
console.log(getResult());
}
});
const eps = 1e-5;
function getResult() {
while (r - l >= eps) {
let k = (r - l) / 3;
let ml = l + k;
let mr = r - k;
if (f(ml) > f(mr)) r = mr;
else l = ml;
}
return l;
}
function f(x) {
let ans = 0;
for (let i = n; i >= 0; i--) {
ans += Math.pow(x, i) * a[n - i];
}
return ans;
}
Python
# 输入获取
n, l, r = map(float, input().split())
n = int(n)
a = list(map(float, input().split()))
def f(x):
ans = 0
for i in range(n, -1, -1):
ans += pow(x, i) * a[n - i]
return ans
# 算法入口
def getResult(l, r):
eps = 1e-5
while r - l >= eps:
k = (r - l) / 3
ml = l + k
mr = r - k
if f(ml) < f(mr):
l = ml
else:
r = mr
return l
print(getResult(l, r))
近似三等份求解
Java
import java.util.Scanner;
public class Main {
static int n;
static double l;
static double r;
static double[] a;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
l = sc.nextDouble();
r = sc.nextDouble();
a = new double[n + 1];
for (int i = 0; i <= n; i++) {
a[i] = sc.nextDouble();
}
System.out.println(getResult());
}
static double eps = 1e-5;
public static double getResult() {
while (r - l >= eps) {
double mid = (l + r) / 2.0;
if (f(mid - eps) < f(mid + eps)) {
l = mid;
} else {
r = mid;
}
}
return l;
}
public static double f(double x) {
double ans = 0;
for (int i = n; i >= 0; i--) {
ans += Math.pow(x, i) * a[n - i];
}
return ans;
}
}JS
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
let n, l, r, a;
rl.on("line", (line) => {
lines.push(line);
if (lines.length == 2) {
[n, l, r] = lines[0].split(" ").map(Number);
a = lines[1].split(" ").map(Number);
console.log(getResult());
}
});
function getResult() {
const eps = 1e-5;
while (r - l >= eps) {
const mid = (r + l) / 2;
if (f(mid - eps) < f(mid + eps)) l = mid;
else r = mid;
}
return l;
}
function f(x) {
let ans = 0;
for (let i = n; i >= 0; i--) {
ans += Math.pow(x, i) * a[n - i];
}
return ans;
}
Python
# 输入获取
n, l, r = map(float, input().split())
n = int(n)
a = list(map(float, input().split()))
def f(x):
ans = 0
for i in range(n, -1, -1):
ans += pow(x, i) * a[n - i]
return ans
# 算法入口
def getResult(l, r):
eps = 1e-5
while r - l >= eps:
mid = (l + r) / 2
if f(mid - eps) < f(mid + eps):
l = mid
else:
r = mid
return l
print(getResult(l, r))