1206. 设计跳表

不使用任何库函数，设计一个 跳表 。

跳表 是在 O(log(n)) 时间内完成增加、删除、搜索操作的数据结构。跳表相比于树堆与红黑树，其功能与性能相当，并且跳表的代码长度相较下更短，其设计思想与链表相似。

例如，一个跳表包含 [30, 40, 50, 60, 70, 90] ，然后增加 80、45 到跳表中，以下图的方式操作：

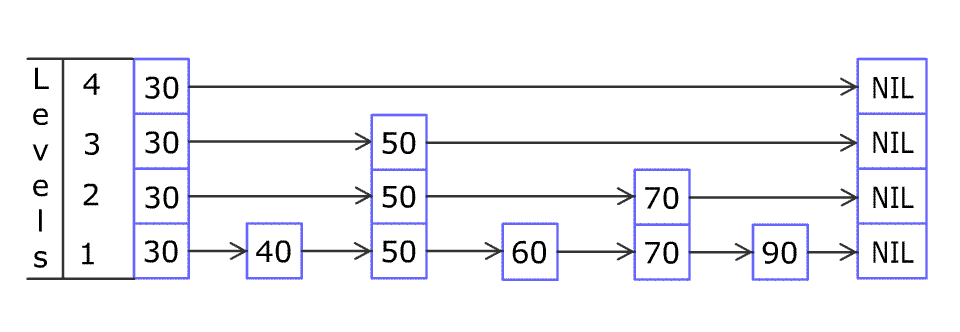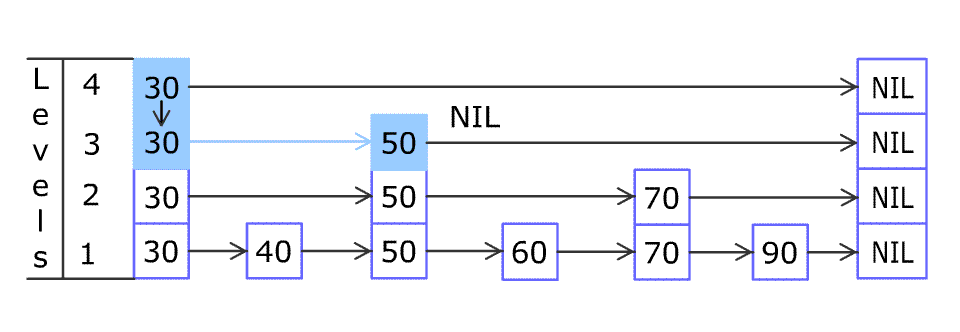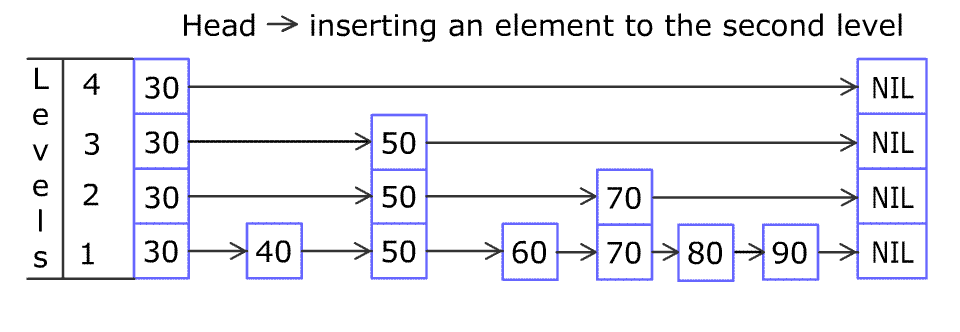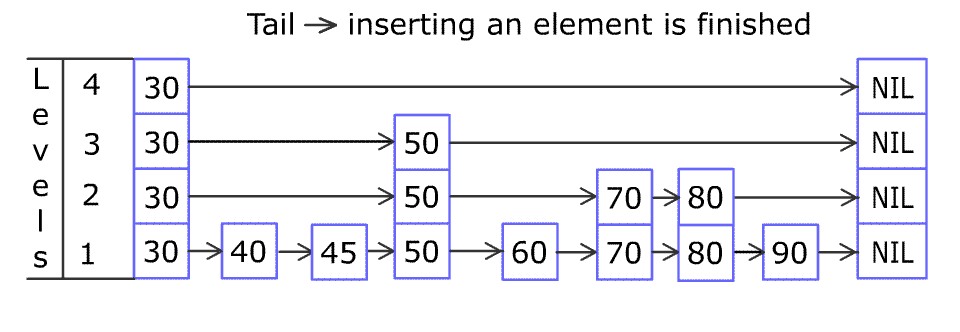
跳表中有很多层，每一层是一个短的链表。在第一层的作用下，增加、删除和搜索操作的时间复杂度不超过 O(n)。跳表的每一个操作的平均时间复杂度是 O(log(n))，空间复杂度是 O(n)。

在本题中，你的设计应该要包含这些函数：

bool search(int target) : 返回target是否存在于跳表中。
void add(int num): 插入一个元素到跳表。
bool erase(int num): 在跳表中删除一个值，如果 num 不存在，直接返回false. 如果存在多个 num ，删除其中任意一个即可。
注意，跳表中可能存在多个相同的值，你的代码需要处理这种情况。

跳表结点 SkipNode

struct SkipNode {
    int val;
    vector<SkipNode*> next;
    SkipNode(int val, int level) :val(val), next(level, nullptr) {};
};

跳表 Skiplist 

class Skiplist {
private:
    SkipNode* head;//头结点（初始化为最高层数） 
    int level;//当前跳表的最高层数（除了头结点） 
public:
    bool search(int target)
    {
        从当前最高层开始遍历，如果当前结点的下一个结点大于target（或者为nullptr），
        则进入当前结点的下一层，继续向右遍历。
    }
    void add(int num)
    {
        创建一个新结点，给它随机一个层数newlevel，然后更新当前最高层数；
        接着从当前最高层开始遍历，如果当前结点的下一个结点大于target（或者为nullptr），
        则让新结点指向当前结点的下一个结点，当前结点指向新结点
        注意：自顶向下，从newlevel ~ 0都要连一次
    }
    bool erase(int num)
    {
        从当前最高层开始遍历，如果当前结点的下一个结点大于target（或者为nullptr），
        则进入当前结点的下一层，继续向右遍历。
        如果当前结点的下一个结点等于target，则让当前结点指向下一个的下一个结点，完成删除
        注意：自顶向下，要删的结点，每一层都要删一次

        删除完成之后，记得更新当前跳表的最高层数       
    }
};

实现代码： 

#include <bits/stdc++.h>
using namespace std;
const int MAX_LEVEL = 8;//最高8层 

struct SkipNode {
    int val;
    vector<SkipNode*> next;
    SkipNode(int val, int level) :val(val), next(level, nullptr) {};
};

class Skiplist {
private:
    SkipNode* head;//头结点（初始化为最高层数） 
    int level;//当前跳表的最高层数（除了头结点） 
public:
    Skiplist() :head(new SkipNode(-1, MAX_LEVEL)), level(0) {}
    int randomLevel()//插入一个新结点时，随机它的层数 
    {
        int rlevel = 1;
        while (rand() % 2 == 0 && rlevel < MAX_LEVEL)//如果随机出 0，层数+1，如果随机出 1，结束递增 
        {
            rlevel++;
        }
        return rlevel;
    }
    //查找 
    bool search(int target)
    {
        SkipNode* cur = head;
        for (int i = level - 1; i >= 0; i--)//从最高层开始 
        {
            while (cur->next[i] != nullptr && cur->next[i]->val < target)//向右遍历，直至当前结点的下一个结点 >= target
            {
                cur = cur->next[i];
            }
            if (cur->next[i] != nullptr && cur->next[i]->val == target)
            {
                return true;
            }
            //如果当前结点的下一个结点 > target，则进入下一层 
        }
        return false;
    }
    //添加 
    void add(int num)
    {
        int newlevel = randomLevel();//随机一个层数 
        if (newlevel > level)//更新 level 
        {
            level = newlevel;
        }
        SkipNode* newNode = new SkipNode(num, newlevel);
        SkipNode* cur = head;
        for (int i = level - 1; i >= 0; i--)
        {
            while (cur->next[i] != nullptr && cur->next[i]->val < num)
            {
                cur = cur->next[i];
            }
            if (i < newlevel)//插入一个新增结点 
            {
                newNode->next[i] = cur->next[i];
                cur->next[i] = newNode;
            }
        }
    }
    bool erase(int num)
    {
        SkipNode* cur = head;
        SkipNode* toDelete = nullptr;
        for (int i = level - 1; i >= 0; i--)
        {
            while (cur->next[i] != nullptr && cur->next[i]->val < num)
            {
                cur = cur->next[i];
            }
            if (cur->next[i] != nullptr && cur->next[i]->val == num)
            {
                toDelete = cur->next[i];
                cur->next[i] = toDelete->next[i];//在 当前这一层 上删除目标结点 
            }
        }
        //更新 level 
        while (level >= 1 && head->next[level - 1] == nullptr) {
            level--;
        }
        //delete 防止内存泄露 
        if (toDelete != nullptr) {
            delete toDelete;
            return true;
        }
        else {
            return false;
        }
    }
};

int main()
{
    Skiplist* skiplist = new Skiplist();
    skiplist->add(1);
    skiplist->add(2);
    skiplist->add(3);
    cout << skiplist->search(0) << endl;   // 返回 0
    skiplist->add(4);
    cout << skiplist->search(1) << endl;   // 返回 1
    cout << skiplist->erase(0) << endl;    // 返回 0
    cout << skiplist->erase(1) << endl;    // 返回 1
    cout << skiplist->search(1) << endl;   // 返回 0
}