目录
1. 概述
2. 指定软件设计
3. 验证设计规范
4. 验证预期属性
1. 概述
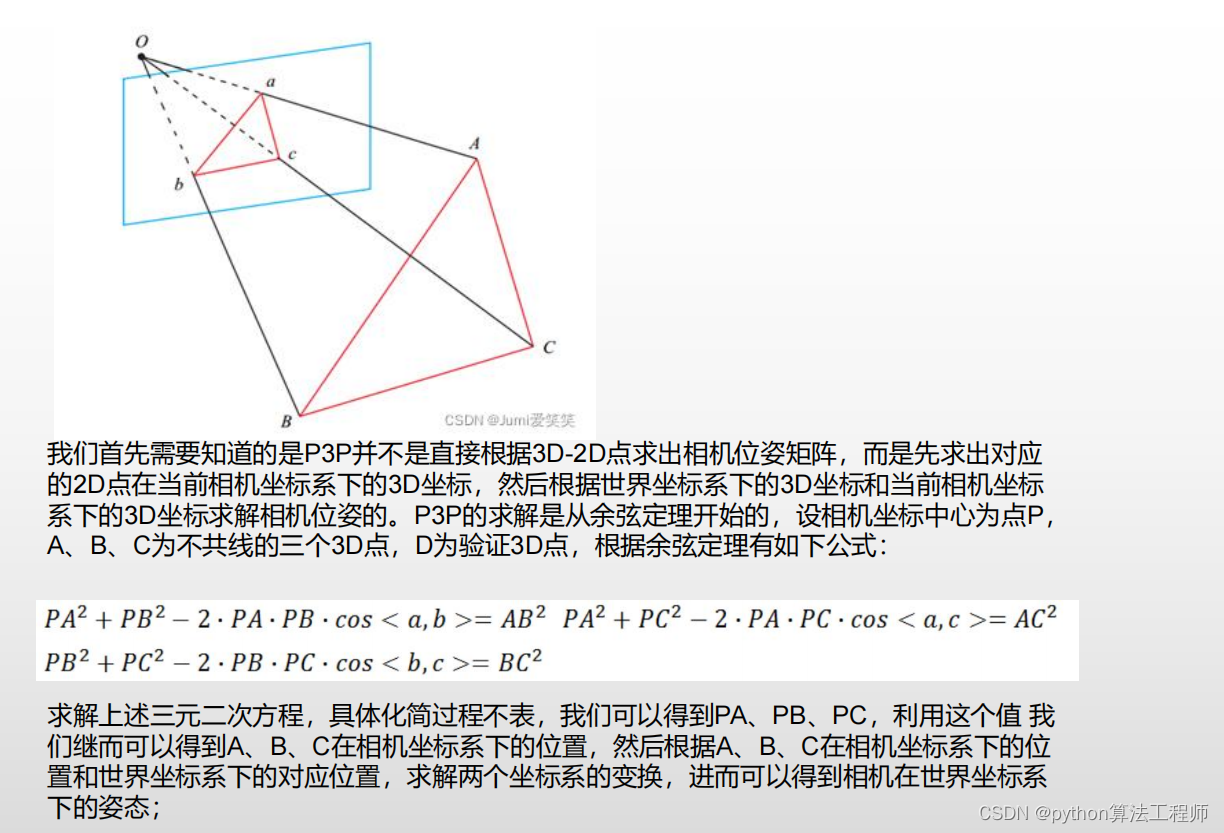
在第一章中,我们将解释如何使用 Alloy 来探索一个非常简单的软件组件的设计,即大多数操作系统中存在的众所周知的垃圾箱 或回收站。目的是对如何使用 Alloy 指定和分析软件设计进行简要的(有时是肤浅的)概述。Alloy 规范语言和分析技术的全部细节将在以下章节中给出。

Trash 的目标是:
- 1. 使已删除的文件仍然可以恢复,直到执行清空 Trash 的(可撤消的)操作
- a. 当文件被删除时,它存储在 Trash 中;
- b. 仍在 Trash 中时,可以恢复文件;
- c. 清空后,Trash 中包含的所有文件将被永久删除。
- b. 仍在 Trash 中时,可以恢复文件;
- a. 当文件被删除时,它存储在 Trash 中;
更具体地说,在本章中,我们将展示如何在以下任务中使用 Alloy:
-
在非常抽象的层次上正式指定垃圾桶组件的结构和行为的设计。
-
通过仿真验证此设计,即使用 Alloy Analyzer 检查它是否允许 Trash 的某些预期行为。
-
引出并验证 Trash 组件的一些预期属性。
2. 指定软件设计
转换系统(Transition systems)是推理系统行为最标准的形式主义之一,是描述和推理软件系统设计的一种非常方便和抽象的形式主义。转换系统包含系统在随时间演化时可能处于的不同状态(states),识别其中哪些是可能的初始状态(initial states),并通过识别将每个状态连接到每个可能的后续状态的转换(transitions)来清楚地描述系统如何演化。
指定转换系统的第一步是描述其状态的结构。在 Alloy 中:
系统的结构是根据集合(sets)和关系(relations)来描述的。
集合(sets)称为签名(signatures),并使用关键字
sig声明,后跟强制签名名称和括在大括号之间的可选字段(field)声明列表。
字段(fields)是将封闭签名的元素连接到其他元素的关系(relations)。
我们不会在本章中使用字段,因此我们在本例中的签名声明在名称后总是有一对空括号。
在 Alloy 中,签名由所谓的原子(atoms)组成,没有任何内部结构或任何特定语义的元素,其名称将由 Analyzer 自动生成。默认情况下,在 Alloy 中,所有签名和关系的值都是不可变的。要声明可变(或变量)签名,只需 var 在签名声明之前添加关键字。
在非常抽象的层面上,我们可以使用两个集合来描述 Trash 组件的状态:文件系统中随时存在的文件集合,以及当前在垃圾桶中的文件的子集。因此,在我们的 Alloy 规范中,我们将分别声明两个变量签名:File 和 Trash。为了表明后者是前者的子集,在声明中, Trash 我们将使用关键字 in 后跟包含签名的名称。因此,Trash state 的 Alloy 规格如下。
var sig File {}
var sig Trash in File {}
在这个例子中,签名 File 是一个顶级签名(top-level signature),不包含在任何其他签名中,而是 Trash 一个子集签名(subset signatur)。
在 Alloy 中,所有顶级签名都是不相交的。可变顶级签名也是如此:
它们总是不相交的,即使在不同的时间点,这意味着原子(atoms)不能在状态转换中从一个顶级签名移动到另一个顶级签名。
在描述了我们系统的状态之后,我们现在可以继续指定它的预期行为,即 Trash 转换系统的初始状态和转换是什么。与许多正式规范语言不同,Alloy 没有特殊的语法来声明此转换系统。相反,它遵循 Leslie Lamport 在动作的时间逻辑(Temporal Logic of Actions)中引入的想法,即通过一个时态逻辑公式来隐式地指定转换系统,该公式识别哪些是其有效的执行轨迹。
轨迹(trace)是无限的状态序列,充分描述了系统的可能行为。
指定转换系统的公式通常由两部分组成:
- a. 一个公式指定什么是有效的初始状态;
- b. 另一个指定每个状态下可能的转换。
在我们的示例中,在初始状态下我们有一个空垃圾桶。要测试一组是否为空,我们可以使用关键字 no,后面跟要检查的集合表达式(为了检查它是否为非空,我们可以使用关键字 some,并检查它是否至多包含一个元素,关键字 lone)。要施加约束以限制系统的有效痕迹,我们可以使用关键字 fact 后跟一个可选的名称和一个用大括号括起来的公式。如果该公式不包含时间运算符,即如果它是一个普通的一阶公式,它约束状态中的集合和关系的值,那么它只需要保持在每条轨迹的初始状态。在我们的示例中,有效的初始状态因此可以由以下事实指定。
fact init {
no Trash
}
要指定有效的转换,首先考虑系统中的事件(events)(或操作)会更容易。每个事件都会引发许多转换。对于垃圾箱组件,我们有三个事件:
- a. 删除文件
- b. 恢复文件
- c. 清空垃圾箱
要指定一个事件,我们将编写一个公式,该公式适用于轨迹的特定状态,前提是该事件可以在该状态下发生,并且轨迹的下一个状态是该事件的有效结果。这两个条件通常分别称为守卫(guard)和事件的影响(effect)。为了指定影响,我们需要以某种方式评估下一个状态下公式的值,或者参考下一个状态下集合和关系的值。为了评估下一个状态下的公式,我们在它前面加上时间运算符 after。为了评估下一个状态下的表达式,我们将其附加操作符'。出于可读性原因,在单独的谓词(predicates)中指定每个事件很方便。
谓词是一个命名的公式,只有在调用时才会成立(例如在事实中)。
要声明谓词,应使用关键字 pred,后跟谓词名称、可选的谓词参数列表和括在花括号中的公式。例如,空垃圾事件可以通过以下三个公式的结合来指定。
pred empty {
some Trash and // guard
after no Trash and // effect on Trash
File' = File - Trash // effect on File
}
第一个条件是我们事件的守卫,它声明垃圾桶只能在集合 Trash 包含一些文件的状态下清空。在守卫之后,我们有两个条件来指定它的影响。在指定事件时,我们应该考虑它对构成状态的所有变量集和关系有何影响。
如果没有关于特定变量集或关系的任何规定,那么将没有限制该集合或关系如何演变的约束,这意味着它可以在事件发生时自由变化。
如果意图是让该集合或关系在事件发生时保持不变,则必须添加一个明确的公式,说明下一个状态的值与当前值相同。
这种“不变”的效果条件通常称为帧条件(frame conditions)。
在空垃圾事件的情况下,第一个效果条件表明在下一个状态下 Trash 集合将为空(此效果也可以由 no Trash' 指定),第二个效果条件表明,下一个状态的 File 集的值是从当前值(操作符 - 表示集合差异、 & 集合交集和 + 集合联合)中减去 Trash 中的文件集的结果。
Tip - 提高规范的可读性
Alloy 对布尔运算符有双重语法:它们既可以用典型的编程语言风格的运算符编写,也可以使用各自的英文单词。我们有 ! 和 not 用于否定、&& 和 and 用于关联、|| 和 or 用于分离、=> 和 implies 用于蕴涵,<=> 和 iff 用于等价。Alloy 语法被设计得非常简洁和可读。操作符英文版的使用进一步增加了规范的可读性,将成为本书的首选风格。在一个 fact 或 predicate 中,写在不同行的公式是隐式连接的,因此在 empty 谓词的前两行结尾处的 and 关键字是不需要的,省略它们进一步增加了事件规范的可读性。
当文件(当前不在垃圾桶中)被移动到垃圾桶时,会发生删除文件事件。此事件可以由以下谓词指定,由要删除的文件参数化。请注意帧条件 File:将文件移动到垃圾箱不会永久删除它,因此文件系统中的文件集保持不变。
pred delete [f : File] {
not (f in Trash) // guard
Trash' = Trash + f // effect on Trash
File' = File // frame condition on File
}
Important - 一切都是一个集合(set)!
细心的读者可能想知道这个谓词类型中的表达式 Trash + f 是如何检查的,因为联合运算符被应用于set Trash 和 file atom f。在 Alloy 中,每个表达式都表示一个集合,特别是变量的值是一个只包含该变量值的单例集合。所以 Trash + f 中的 f 是一组文件,就像 Trash 一样,可以计算两者的并集。乍看之下,这可能有些奇怪,但这正是 Alloy 的优秀细节之一,进一步简化了它的语义和语法(通过大幅减少语言中运算符的数量)。另一个例子是 in 操作符,它实际上测试集合包含而不是像人们可能期望的那样设置成员资格。同样,因为 f 表示一个单例集,所以 Trash 中的表达式 f 间接地检查 f 是否是 Trash 的成员,所以同样的 in 操作符可以很容易地用于这两个目的。
恢复文件事件规范与删除文件事件规范非常相似。
pred restore [f : File] {
f in Trash // guard
Trash' = Trash - f // effect on Trash
File' = File // frame condition on File
}
指定了我们的三个事件后,我们现在需要约束系统的有效转换。这可以通过强加一个事实来实现,即在系统演化过程中的每个可能状态下,三个事件之一必须成立。为了对轨迹的所有状态施加约束,我们可以使用时间运算符 always 后跟所需的公式。使用此运算符,我们可以轻松地指定 Trash 组件示例的有效转换,如下所示。
fact trans {
always (empty or (some f : File | delete[f] or restore[f]))
}
请注意存在量词 some 的用法,以在每个状态下“选择”要删除或恢复的文件。
3. 验证设计规范
现在我们已经有了 Trash 组件预期行为的第一个规范,在继续验证其预期属性之前,建议对其进行验证以检查其行为是否确实符合预期。执行此类验证的典型方法是使用某种用户引导的模拟。Alloy Analyzer 有多种机制,允许用户探索和验证设计,包括一个交互式探索模式类似的模拟。
Alloy 的一个显着特征是分析命令( commands)可以与规范中的声明和事实一起包含在内。有两个分析命令,都接受谓词或括在大括号中的公式(在这种情况下是一个可选的命令名称):
命令
run指示分析器检查公式(和声明的事实)的可满足性,如果是的话,产生一个令人满意的实例(instance);
check命令指示分析器检查公式的有效性(假设声明的事实为真),如果不是这样则产生一个反例实例(counter-example instance)。
在具有可变集合(mutable sets)和关系(relations)的规范的情况下,一个实例是一个有效的执行轨迹,一个无限的状态序列,每个状态都是对声明的集合和字段的评估。
Note - 实例还是模型?
在介绍逻辑的语义时,公式的实例通常被称为模型:一个公式的模型是其自由变量的估值,使该公式为真。在 Alloy 中,术语模型经常被用来表示系统的规范,而术语实例则被用来表示满足的估值。在 Alloy 的说法中,模型一词的使用与其他软件设计的技术和语言是一致的,即统一建模语言,其中软件模型正是我们用规范表示的那种人工制品。
Alloy的另一个显著特点是,分析命令返回的实例以图形的形式描述:
属于不同集合的原子是节点(以方框描述),关系是边(以箭头描述)。此外,这种图形描述可以使用主题(themes)进行定制,即可以根据节点和边所属的集合和关系来定制其颜色和形状。
开始验证一个规范的通常方法是定义一个空的 run 命令:一个空的公式等同于真,这个命令基本上要求一个满足所有声明事实的实例。如果没有返回,那么事实是不一致的,很可能我们的系统规范有问题,需要纠正。为了启动模拟过程,我们将在我们的规范中添加一个空命令(名为example)。
run example {}
要执行一个规范的单个命令,或重新执行最后一个命令,只需按 cmd-e 或分析器窗口工具栏上的Execute 按钮。如果你有多条命令,要选择执行哪一条,请到 Execute 菜单中选择需要的命令。如果命令被命名,你会看到名称,否则你会看到一个自动生成的名称,由命令的类型(run 或 check)组成,后面是 $ 和一个连续的数字标识。在执行了这个 example 的命令后,我们得到了以下实例。

这里我们看到的是符合我们规范的执行轨迹的描述。在工具栏下面,Alloy 可视化器显示了实例轨迹的描述,在这种情况下,它由两个状态组成,第二个状态之后是回到初始状态的循环。因此,这个轨迹是两个状态的无限交替序列。Alloy Analyzer 返回的所有轨迹都是这种类型:一个有限的状态序列,然后循环回到之前的一个状态。所有的执行轨迹都是无限的,但该工具只返回和描述那些可以用回环来有限地表示的轨迹。在窗口的下半部分,可视化工具专注于轨迹的特定转换,以典型的 Alloy 风格描述前状态和后状态:原子根据其所属的签名依次命名,属于子集签名(如 Trash)的原子用该签名名称标记。可变集合(Mutable sets)(和关系(relations))默认是用虚线画的,但这可以在主题中改变。被描述的两个状态是在轨迹中显示为白色的状态,所有的状态在轨迹描述中都会保持中心位置。当 visualizer 窗口弹出时,被描述的 transition 总是第一个,左边的状态是轨迹的初始状态。在这个例子中,我们可以推断出第一个转换是由于一个文件的删除:最初我们有一个不在垃圾箱中的文件,而在第二个状态中这个文件在垃圾箱中:唯一可能导致这个转换的事件是一个删除。
要在轨迹中导航,即向前和向后移动以关注不同的转换,只需分别按工具栏中的 → 或 ← 按钮(或者是 cmd-→ 和 cmd-←)。例如,通过继续关注第二个转换,我们得到以下结果。
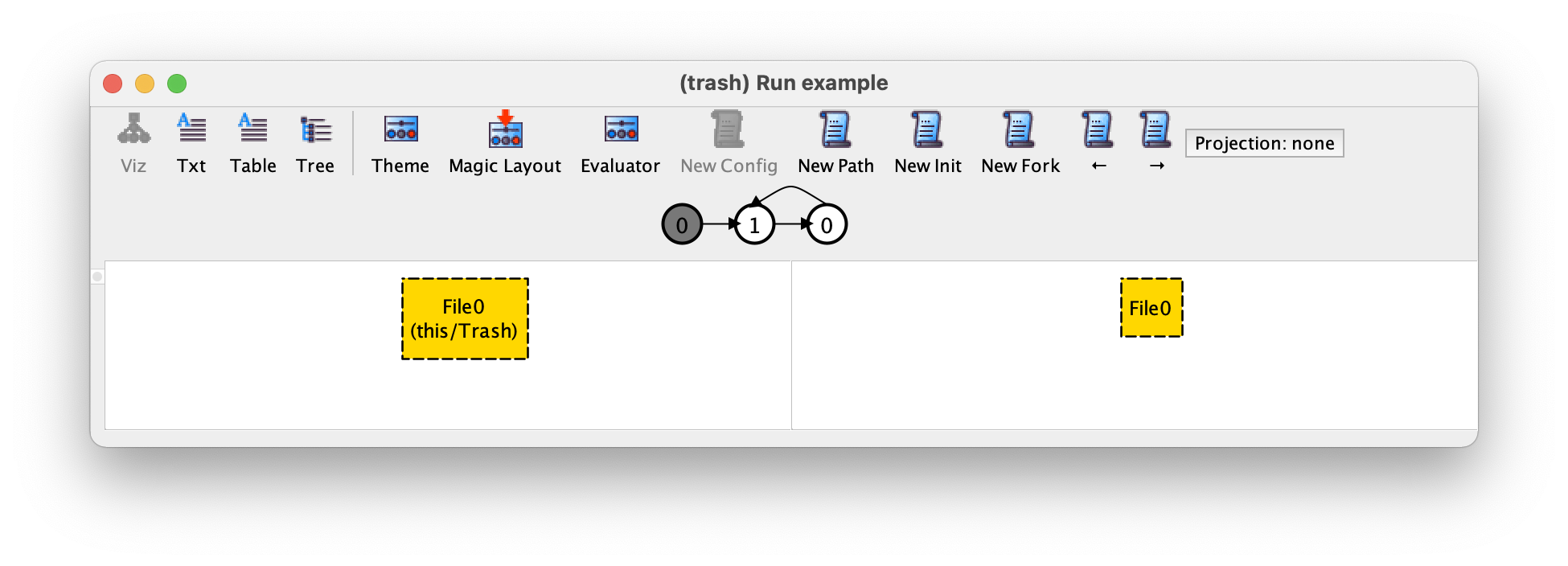
第二个转换是由一个恢复事件引起的:在前状态下,File0 在垃圾桶中,而在后状态下,它不再存在。因此我们可以得出结论,我们的第一个实例是在删除和立即恢复 File0 之间的无限交替,这是系统的有效执行。
Note - 显示与转换(transition)对应的事件。
Alloy 实例可视化器(visualiser)并不显示与转换相对应的事件。实际上,Alloy 中没有事件的概念:我们的事件是由三个正常的逻辑谓词来模拟的,所以可视化器没有办法知道这些是应该被特别处理的事件。另一个问题是,一个转换可能不只对应于一个事件:经常有两个不同的事件可以引起同一个转换,在这个抽象的规范层面上,没有办法(也没有兴趣)区分哪一个实际发生。在大多数例子中,也就是像我们的运行例子这样简单的例子中,推断哪个事件发生是有点微不足道的。然而,在一些更复杂的设计中,情况就不是这样了。在 Alloy 建模技巧一章中,我们将介绍一个Alloy idiom,它允许将可能导致每个转换的事件的名称(或名称)可视化。
在 Alloy 实例可视化窗口的工具栏上,我们可以找到三个按钮,可以用来要求分析器提供替代实例:
New Config
这个按钮要求得到一个新的轨迹,这个轨迹在不可变的集合和关系的值上有所不同。通常情况下,不可变的元素构成了系统的配置(configuration)(例如,描述一个要执行协议的特定网络拓扑结构),按下这个按钮,我们将得到一个具有不同配置的执行轨迹。在这个例子中,我们所有的集合都是可变的,所以这个按钮是不适用的,是灰色的。
New Path
此按钮要求一个新的(不同的)执行轨迹(又名路径)。
New Init
这个按钮要求用不同的初始值对可变集合和关系进行新的追踪,使我们能够快速探索从不同初始条件开始的情景。
New Fork
最后,这个按钮要求提供一个不同的轨迹,其行为直到我们目前关注的(左侧)前状态为止,但在这一点上有不同的转换。如果可以的话,前状态将保持不变,我们将看到一个不同的后状态。后状态可能是同一(非决定性)事件的不同结果,或者是不同事件的结果。
例如,如果此时我们按下 New Fork,我们可以获得以下实例。
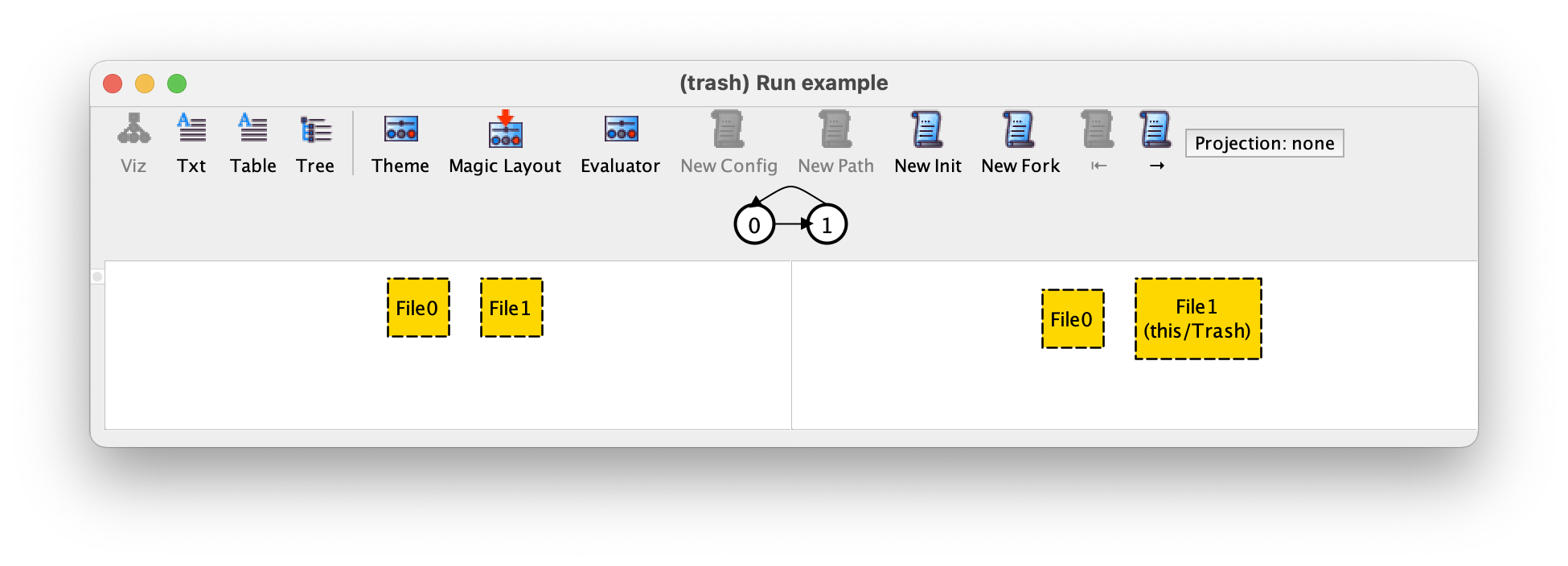
我们现在在初始状态下有两个不同的文件,只是 File1 被删除了。如果我们按 → 我们可以看到在第二次转换中这个文件被恢复了。
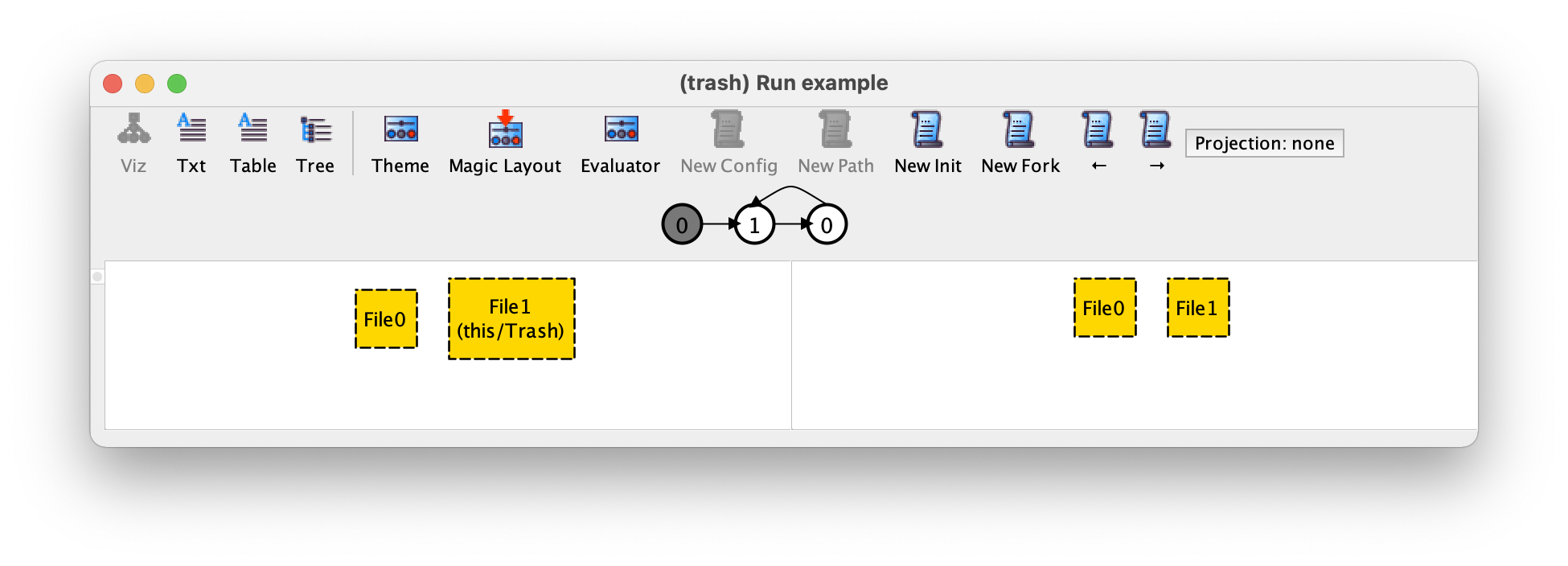
如果现在我们按 New Fork,我们会得到以下轨迹。
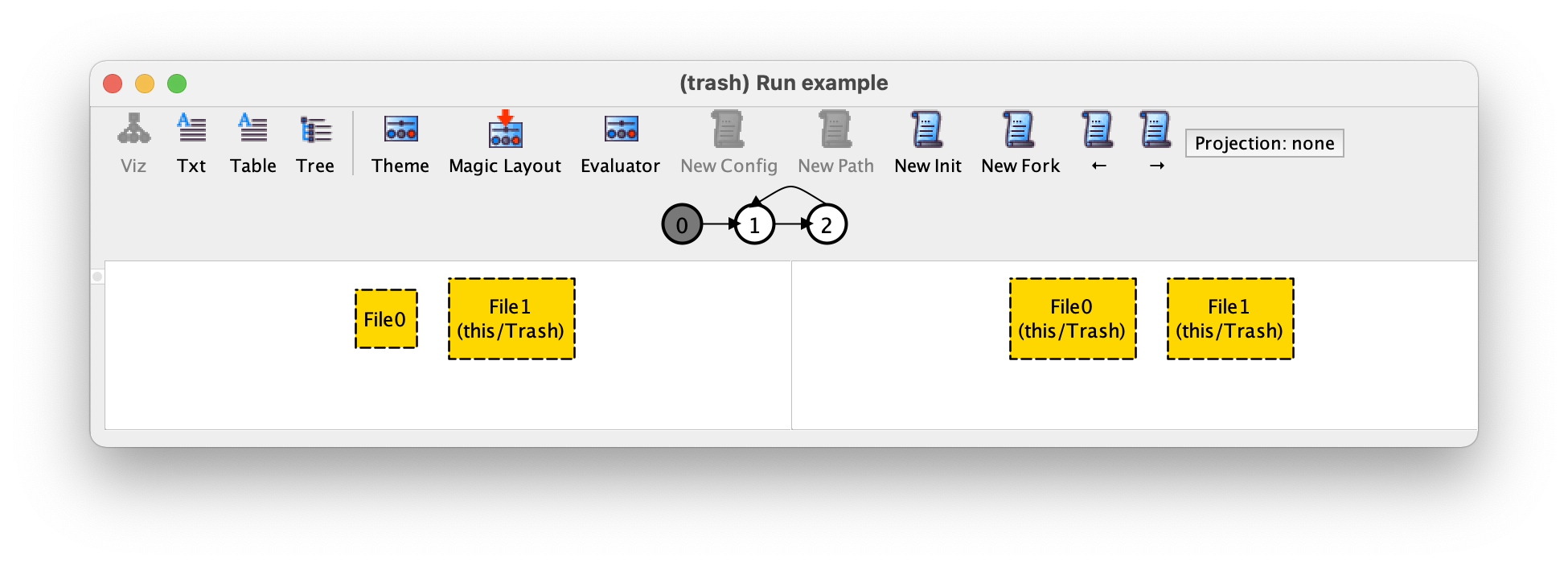
在这个轨迹中,第二个转换是另一次删除(文件 File0)而不是恢复(文件 File1)。现在我们的轨迹从删除文件 File1 开始,然后是删除和恢复文件 File0 的无限次交替。New Fork 是验证设计规范时使用的主要工具,因为它允许我们以一种与其他形式化验证或模型检查工具中的模拟非常相似的方式探索替代行为。
在继续验证我们的设计之前,让我们自定义我们的可视化,例如为垃圾桶中的文件设置不同的颜色。要做到这一点,只需按下工具条上的 Theme 按钮。在左侧,你会看到许多主题定制选项。只要选择 Trash 这一设置,并在左上方的第一个下拉菜单中选择红色,如下所示。
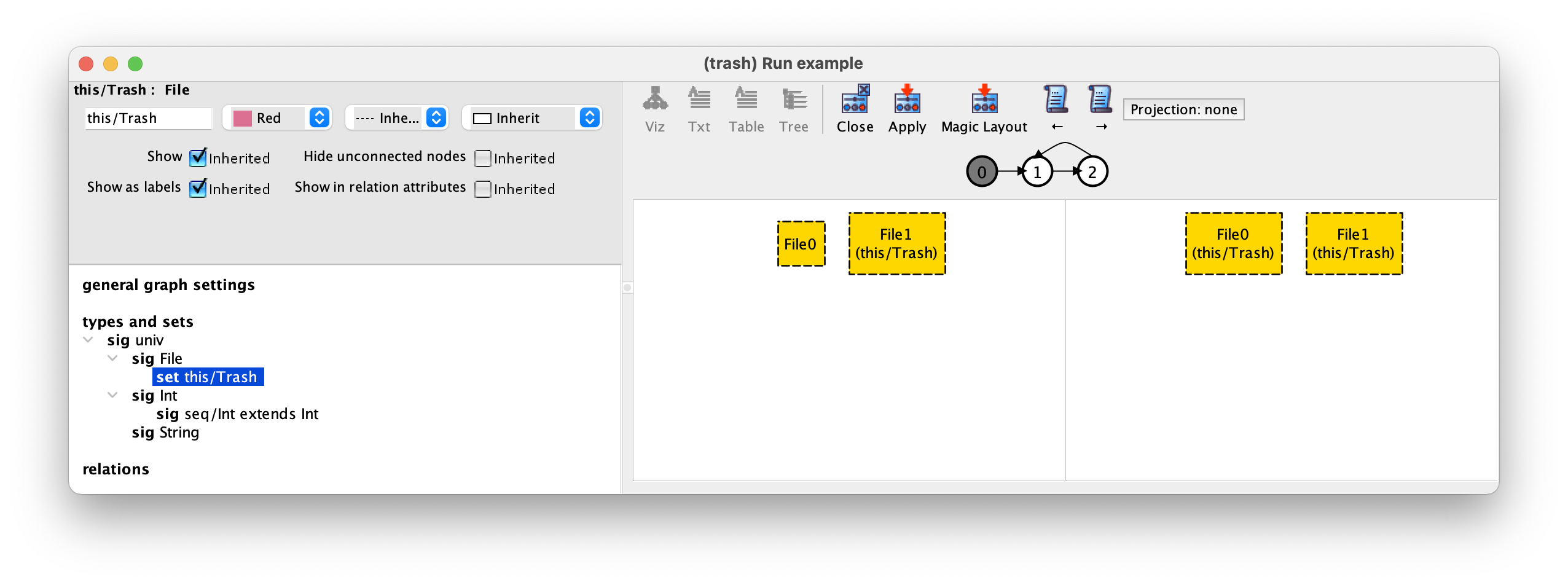
在工具栏中选择 Apply 然后 Close 后,我们的轨迹现在将显示如下。
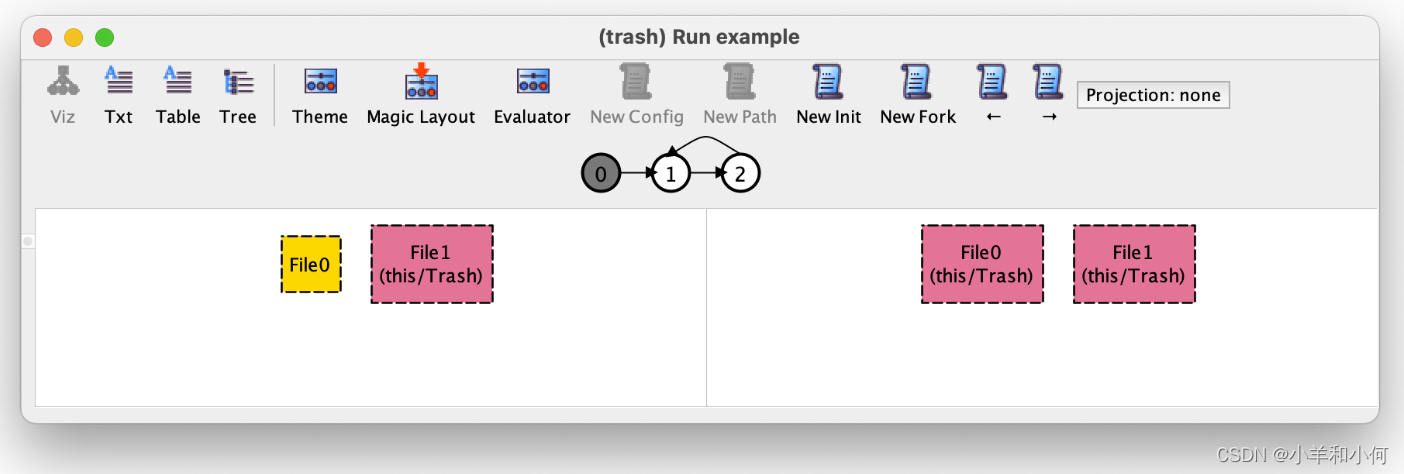
主题自定义菜单中有很多选项,在处理更大更复杂的系统时,这将成为一个非常有用的功能,有助于更好地理解执行轨迹。
如果我们现在按下 New Init,再次要求对我们的文件集进行不同的初始估值,我们会得到以下轨迹,最初我们在文件系统中有三个文件而不是两个。
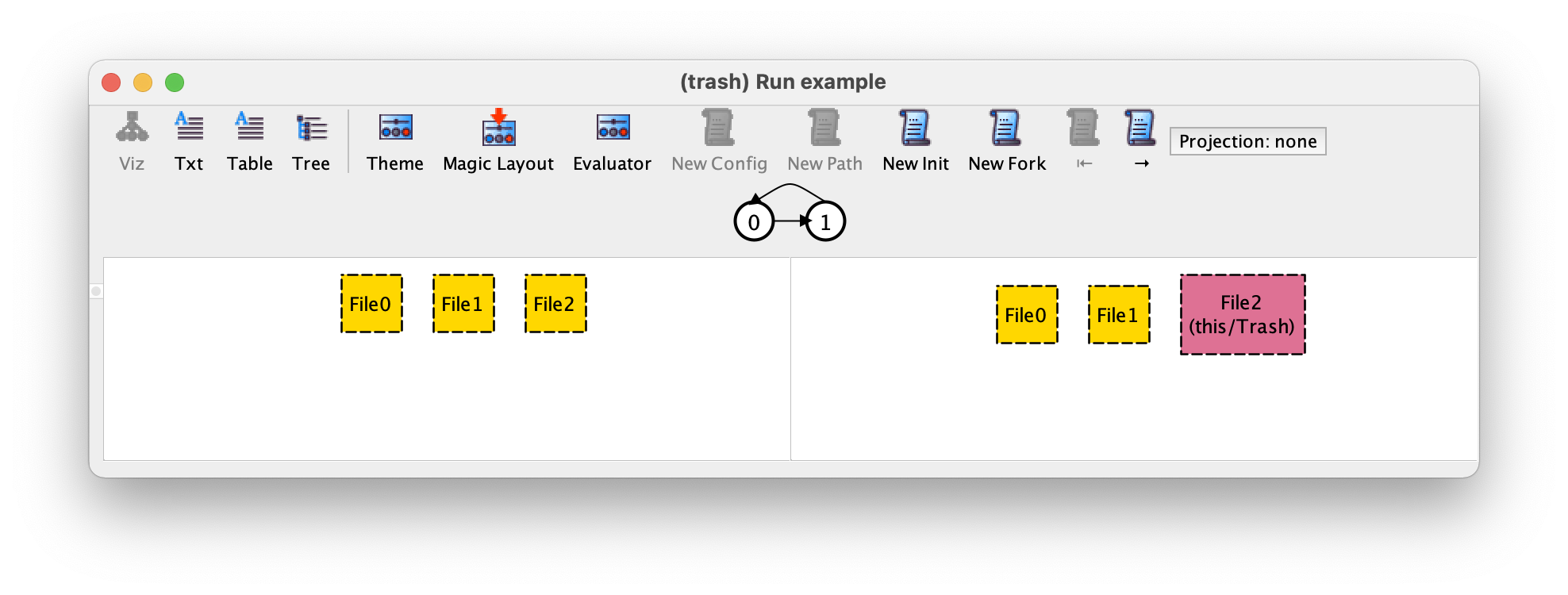
再按一次 New Init,我们得到以下信息。
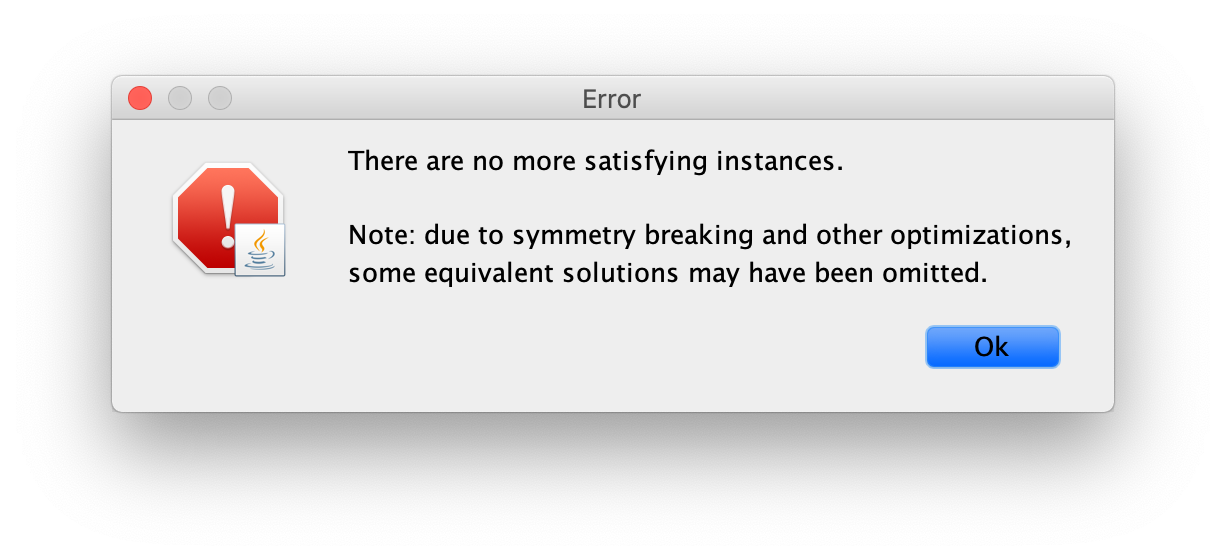
这起初可能看起来相当令人惊讶。首先,为什么分析器没有返回实例,例如,最初我们有三个以上的文件!?第二,为什么分析器没有返回这样的实例,例如,最初有两个名为 File1 和 File2 的文件,而不是上面的 File0 和 File1!?前一种情况是由于作用域(scopes)造成的。为了实现自动分析,Alloy 对所有签名的大小施加了一个约束。这个约束是由命令的范围定义的。默认情况下,所有顶级签名的范围是3,这意味着每个顶级签名最多只能使用三个原子来构建实例。这个范围可以通过在命令后面使用关键字 for 来改变,然后再加上所有顶层签名所需的全局范围。也可以为特定的签名设置不同的作用域,方法是在这个全局作用域后面加上关键字 but 和一个以逗号分隔的不同签名的作用域列表。例如,如果我们的 run 命令是
run example {} for 5
所有顶级签名的范围(在本例中仅为 File)设置为 5。如果我们按几次 New Init,我们可以获得以下实例:
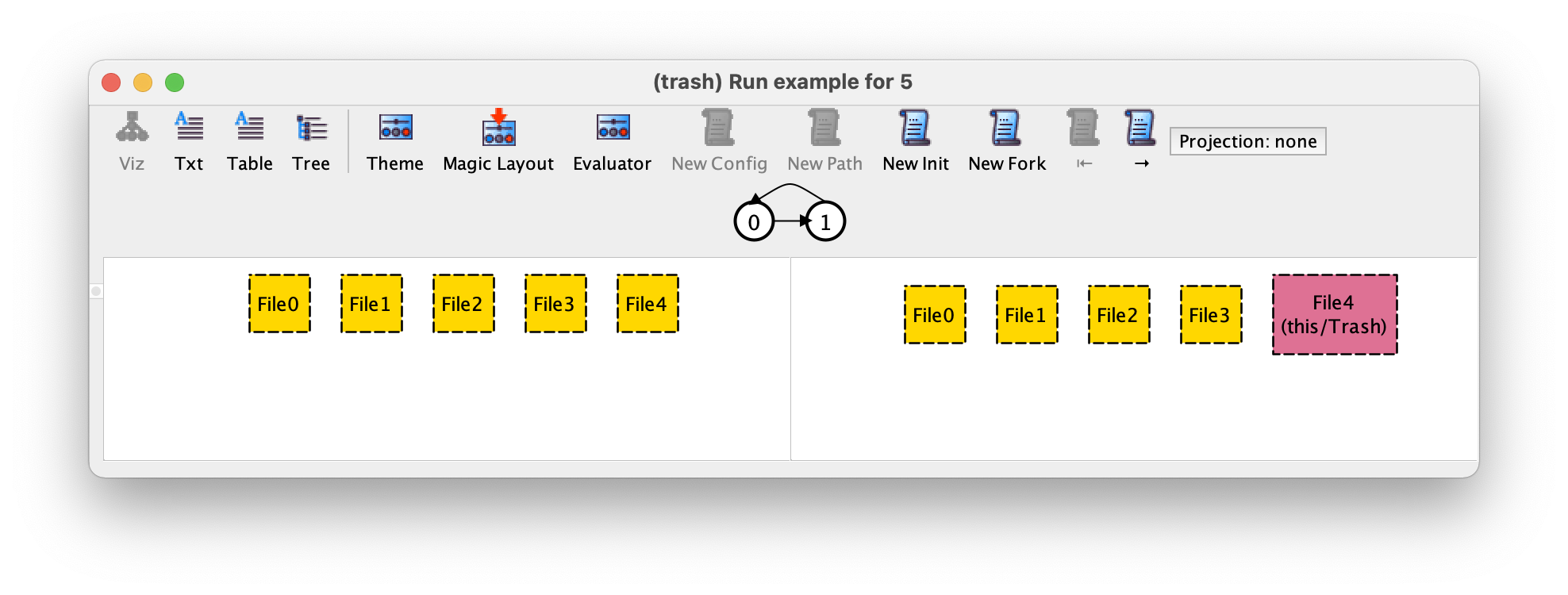
第二个省略是由于对称性破坏(symmetry breaking)。如前所述,原子没有附带语义。特别是,Analyzer 为它们创建的名字是没有意义的: File0 并不是现实世界文件系统中存在的一个特定文件的名字,而只是一个随机的名字,以帮助我们将其与其他文件区分开来。因此,两个仅在原子名称上有差异的实例实际上是同一个实例(它们在原子重命名方面是同构的),向用户展示这两个实例只会妨碍对规范的理解。为了避免这种情况,同时也为了加快分析速度,Analyzer 实现了一个强大的对称性破坏机制,将大多数同构(对称)实例排除在搜索之外。
为了结束我们的验证,让我们试着用分析器找到一个具体的轨迹例子,即最初我们有一个单一的文件,然后被删除,最后垃圾箱被清空。为了做到这一点,我们重新执行我们的 example 运行命令,获得所需的初始状态。
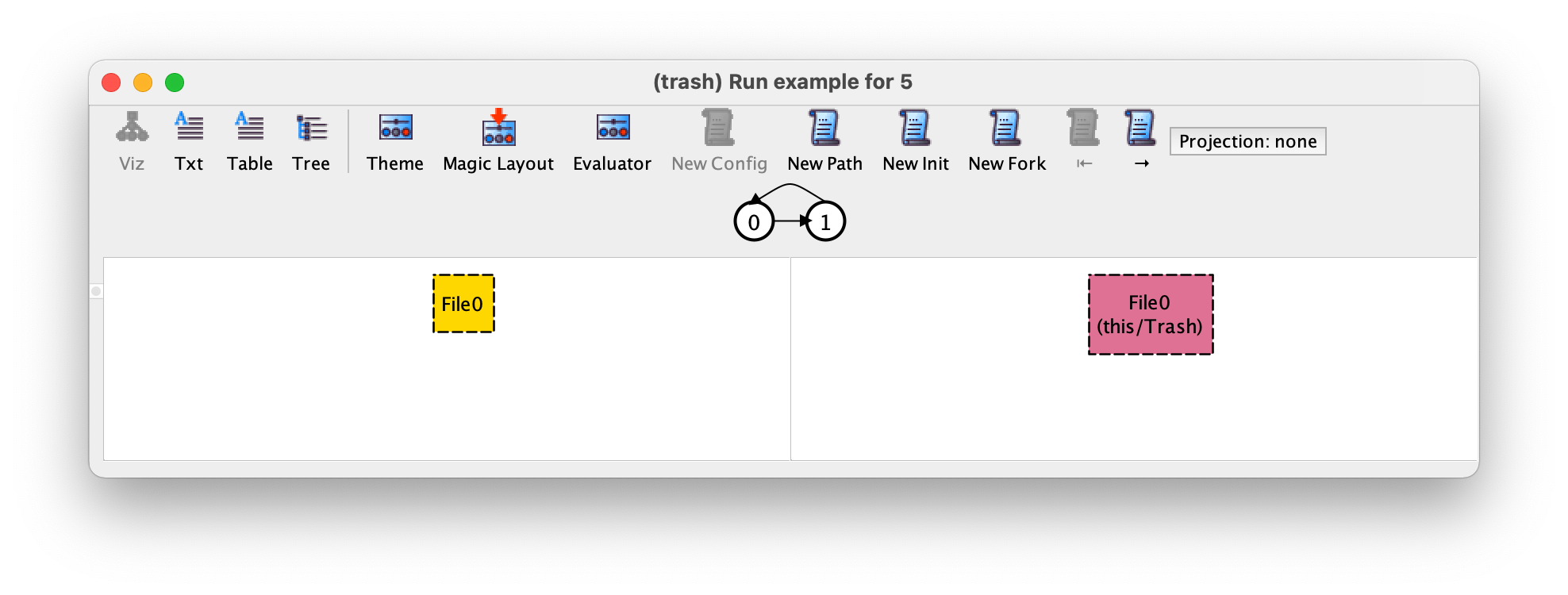
然后我们按 → 移动到第二个转换,它对应于先前删除的文件的恢复。
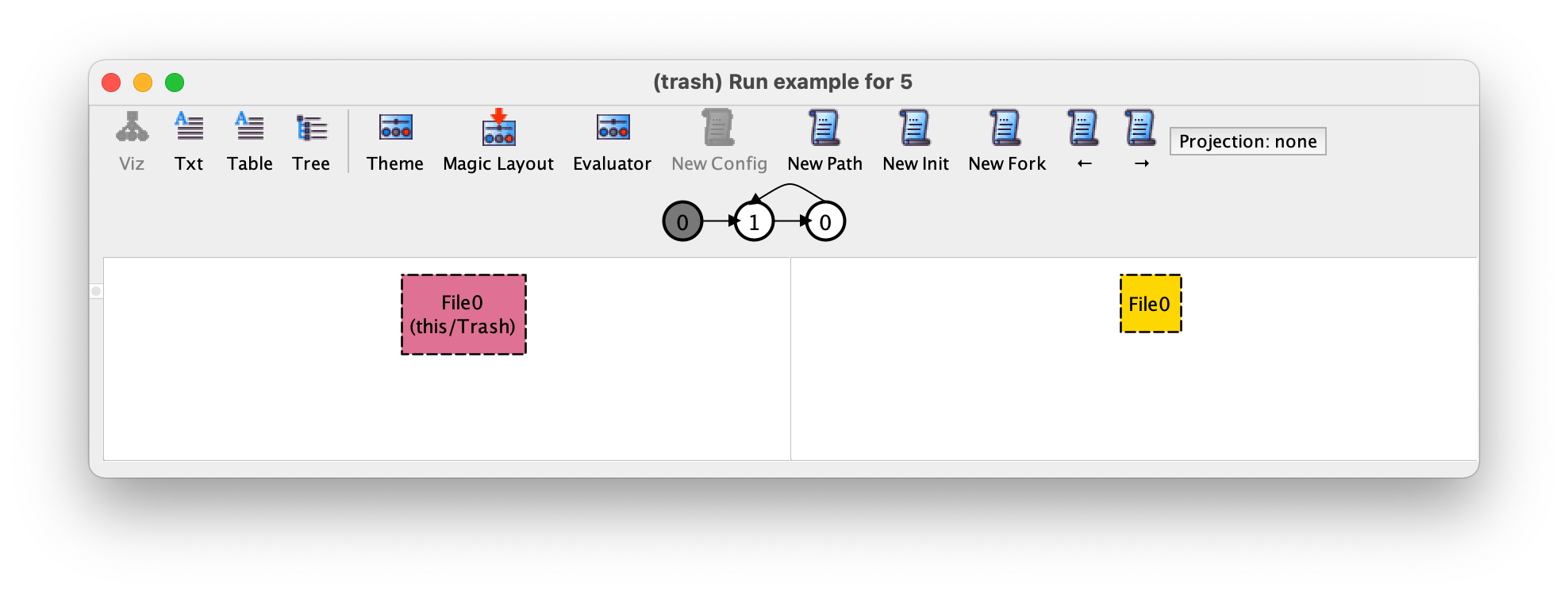
然后,要请求不同的转换,即对应于垃圾清空事件的转换,我们按 Fork。令人惊讶的是,我们得到的不是更令人满意的实例窗口,而不是没有文件的不同下一个状态!

这意味着,我们肯定想在我们的系统中允许这种执行轨迹,但根据我们的规范,目前这种轨迹不认为是有效的。事实上,目前的规范不允许文件系统中的所有文件被永久删除,我们可以通过定义下面的 run 命令来确认,现在有一个公式,要求轨迹到达一个最终没有文件的点。执行这个命令没有产生任何实例,这清楚地表明我们的规范是错误的。
run no_files { eventually no File } for 5
在此命令的公式中,我们使用了时间运算符 eventually:如果接下来的公式至少在轨迹的一个状态上是真的,那么轨迹就满足这个运算符。
那么,我们的规范有什么问题呢?问题在于,事实 trans 规定在任何时间点,三个事件(delete、restore 或 empty)中的一个必须发生。由于 empty 有一个 guard,要求垃圾桶有一些文件,而其他两个事件也要求至少有一个文件存在,所以当没有更多的文件时,这三个事件中没有一个可以发生。这意味着不可能有一个无限的轨迹,其中一个状态没有文件,因为在这一点上不可能有转换。要修复我们的规范,有很多选择。例如,我们可以指定一个允许创建新文件的事件。或者,为了保持我们的规范只关注垃圾箱部分,我们可以添加一个事件,以捕捉我们系统的用户在系统中做其他事情而不影响垃圾箱的可能性(非常真实)。当只考虑我们对垃圾桶的抽象中的集合时,这个事件将完全没有影响,所以这个事件的规范只由框架条件组
pred do_something_else {
File' = File
Trash' = Trash
}
有了这个谓词,我们现在可以按如下方式修复我们对有效转换的规范。
fact trans {
always (empty or (some f : File | delete[f] or restore[f]) or do_something_else)
}
如果我们现在重新执行该no_files命令,我们将获得以下实例,其中我们基本上没有任何文件,虽然有点令人惊讶,但应将其视为我们设计的有效实例。
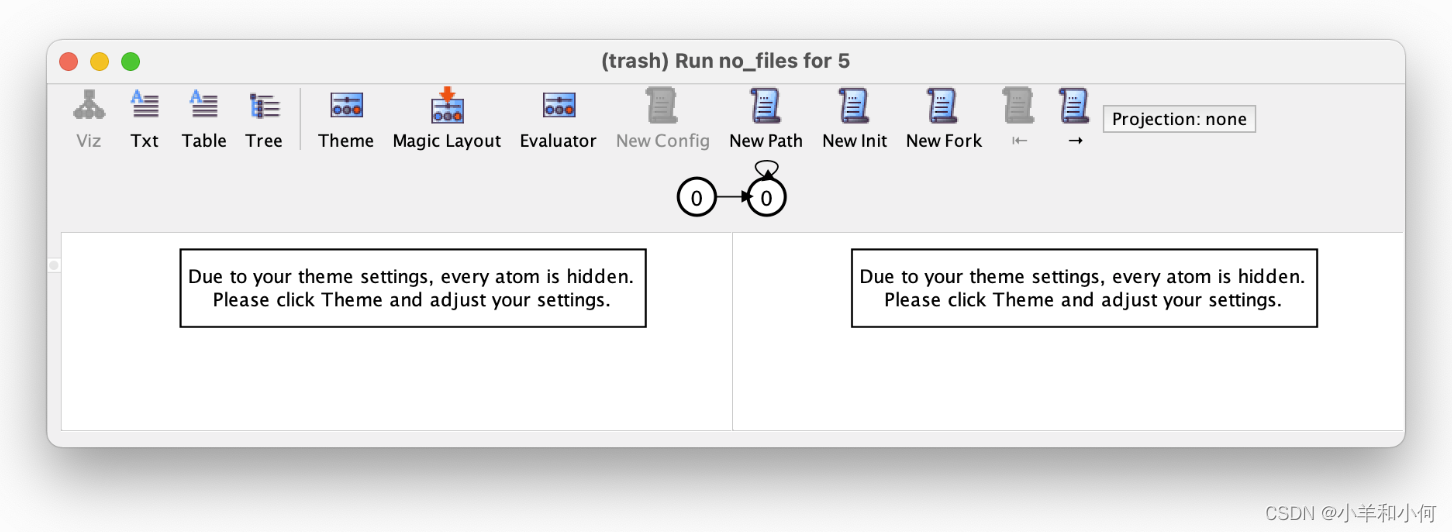
Note - 一个更快的方法来检测我们的问题。
细心的读者可以注意到,其实在这个验证过程中,我们的规范的问题本可以更早地被发现。在
example命令中,当按下 Next Init 来获取初始状态下不同数量的文件的实例时,在得到一个有三个文件的实例后,没有更多令人满意的实例出现了。在这一点上,我们本可以注意到分析器没有得到初始状态下没有任何文件的实例,这本来是可能的。
为了搜索一个最初有一些文件但最终都被永久删除的例子,我们可以从命令的 example 开始做一个 "模拟",使用 → 和 New Fork,直到我们到达一个垃圾箱为空的点,或者直接改变 no_files 命令来直接搜索这样一个例子。
run no_files {
some File
eventually no File
} for 5
回顾一下,如果没有任何时间运算符,添加的约束只适用于第一个状态。执行这个命令会得到一个有单个文件的实例,这个文件被立即删除。通过按下→,我们得到以下对应于清空垃圾的转换。

4. 验证预期属性
Alloy 的一个优点是使用相同的逻辑来指定系统及其预期属性。在许多正式规范语言和验证工具(即大多数模型检查器)中,每种语言都使用不同的语言。在 Alloy 中,我们使用时态逻辑,其中我们已经看到了一些关键运算符,即always和eventually。到目前为止,我们的公式恰好由这些运算符中的一个后跟一些约束组成,因此公式的含义很容易理解:在 的情况下,随后的公式必须在迹线的所有状态下都为真,才能被 always视为有效实例,并且在 eventually该公式必须至少在一种状态下为真。然而,公式可以包含多个这样的运算符,可能是嵌套的,这进一步使它们的理解复杂化。正如时态逻辑入门章节中详述的那样,时态公式实际上是在轨迹的特定状态下计算的。最外层的公式在初始状态下被评估,但嵌套的时间公式可能会在轨迹的不同状态下被评估,具体取决于封闭的时间运算符。因此,时间运算符的(非正式)语义如下:
在验证了我们的设计之后,我们现在开始对它的一些预期属性进行规范和验证。为了举例说明,我们将考虑以下(相当琐碎的)属性,但关于这个例子还可以有更多的规定。
- 每一个恢复的文件都必须是之前被删除的。
- 如果所有的文件都在垃圾桶里,我们清空它,那么就不会再有文件存在。
Alloy 的一个好处是,同样的逻辑被用来指定系统和它的预期属性。在许多形式化的规范语言和验证工具(即大多数模型检查器)中,每一种语言都是不同的。在 Alloy 中,我们使用时间逻辑,我们已经看到了其中的一些关键运算符,即 always 和 eventually。到目前为止,我们的公式正是由这些运算符中的一个加上一些约束组成的,所以公式的含义很容易掌握:在 always 的情况下,接下来的公式必须在跟踪的所有状态下为真,才能被认为是一个有效的实例,而在 eventually 的情况下,公式必须至少在一个状态下为真。然而,公式可以包含几个这样的运算符,有可能是嵌套的,这使它们的理解更加复杂。
一个时态公式实际上是在一个轨迹的特定状态下被评估的。最外层的公式在初始状态下被评估,但是嵌套的时态公式可能在轨迹的不同状态下被评估,这取决于包围的时态操作符。所以,时间运算符的(非正式)语义如下:
always
当在某一特定状态下进行评估时,接下来的公式在该状态和所有后续状态下必须为真。
eventually
当在某一特定状态下进行评估时,接下来的公式必须在该状态下或在以下至少一个状态下为真。
after
当在一个特定的状态下进行评估时,接下来的公式在下一个状态下必须为真(这个状态永远存在,因为痕迹是无限的)。
现在我们将介绍另外几个可能会派上用场的时间运算符。这些时间运算符的性质与上述不同,因为它们制约着过去的行为,而我们到目前为止看到的那些运算符则制约着未来的行为。
historically
当在某一特定状态下进行评估时,接下来的公式在该状态和之前的所有状态下必须为真。
once
当在某一特定状态下进行评估时,接下来的公式必须在该状态或至少在之前的一个状态下为真。
要由 check 命令来验证的属性应该写在断言中。一个断言是用关键字 assert 来声明的,后面是一个标识符,以及一个用大括号括起来的公式。例如,上面的第一个属性可以被指定如下。
assert restore_after_delete {
always (all f : File | restore[f] implies once delete[f])
}
这里我们有一个嵌套时态运算符的例子。最外层的总是规定公式 all f : File | restore[f] implies once delete[f] 在执行轨迹的所有状态下都是真的。这个公式中的 all 是一个普遍的量词,意味着在所有的状态下,restore[f] implies once delete[f] 对该状态下文件系统中的每个文件 f 来说都必须是真的。这个公式规定,只要在某个状态下观察到某个特定文件的还原事件,那么这个文件的删除事件之前一定被观察到。为了验证这个断言,我们可以使用一个 check 命令,后面跟着要检查的断言名称。
check restore_after_delete
这个命令没有产生反例实例,意味着断言很可能是有效的。注意,该命令对顶层签名有一个隐含的范围,所以这个结果意味着断言对最多3个文件的文件系统有效。在 Alloy 中,命令也有一个范围,即在强制回环之前的痕迹的有限前缀的大小。默认情况下,这个范围是10,意味着验证只检查最多有10个不同状态(和转换)的反例轨迹。这是一种被称为有界模型检查的验证技术。Alloy Analyzer 搜索长度增加的反例,并保证返回最短的反例,如果存在的话。要改变这种约束,只需设置特殊签名 steps 的范围。例如,为了验证上述属性,对最多有5个文件的文件系统和最多有20个不同状态的跟踪,范围可以设置如下。
check restore_after_delete for 5 but 20 steps
这个命令也没有产生反例。因此,在这么大的范围内,我们的属性很可能确实是有效的。尽管分析在签名方面总是有界限的,但我们可以在轨迹的大小方面进行无界限的模型检查(unbounded model checking),基本上可以验证由任意数量的状态组成的轨迹的属性。要做到这一点,我们必须首先在 Options 菜单中选择一个支持无界模型检查的求解器。目前,只有 nuXmv 求解器支持这一功能。Solver 是 Analyzer 在后端使用的分析工具,用于执行实际的实例和反例的搜索。对于有界模型检查,可以使用许多不同的求解器:其中一些在特定的例子中可能比其他的快得多,所以如果你的分析命令非常慢,总是值得尝试一下。为了验证我们的属性,对于最多有 3 个文件和任何长度的痕迹的文件系统,范围可以设置为如下。
check restore_after_delete for 3 but 1.. steps
同样,没有找到反例!
第二个属性可以指定如下。
assert delete_all {
always ((Trash = File and empty) implies always no File)
}
Basically, in every state where the formula Trash = File and empty holds (all files are in the trash bin and the empty event occurs) the formula no File (no files exist) must forever hold. To verify this property (with bounded model checking) we could issue the following command.
基本上,在每一个公式 Trash = File and empty 成立的状态下(所有的文件都在垃圾桶里,并且空事件发生),公式 no File(没有文件存在)必须永远成立。为了验证这个属性(使用有界模型检查),我们可以发出以下命令。
Trash = File and emptyno File
check delete_all
令人惊讶的是,这个命令产生了以下具有三种不同状态的反例,我们展示了其中的前两个转换。
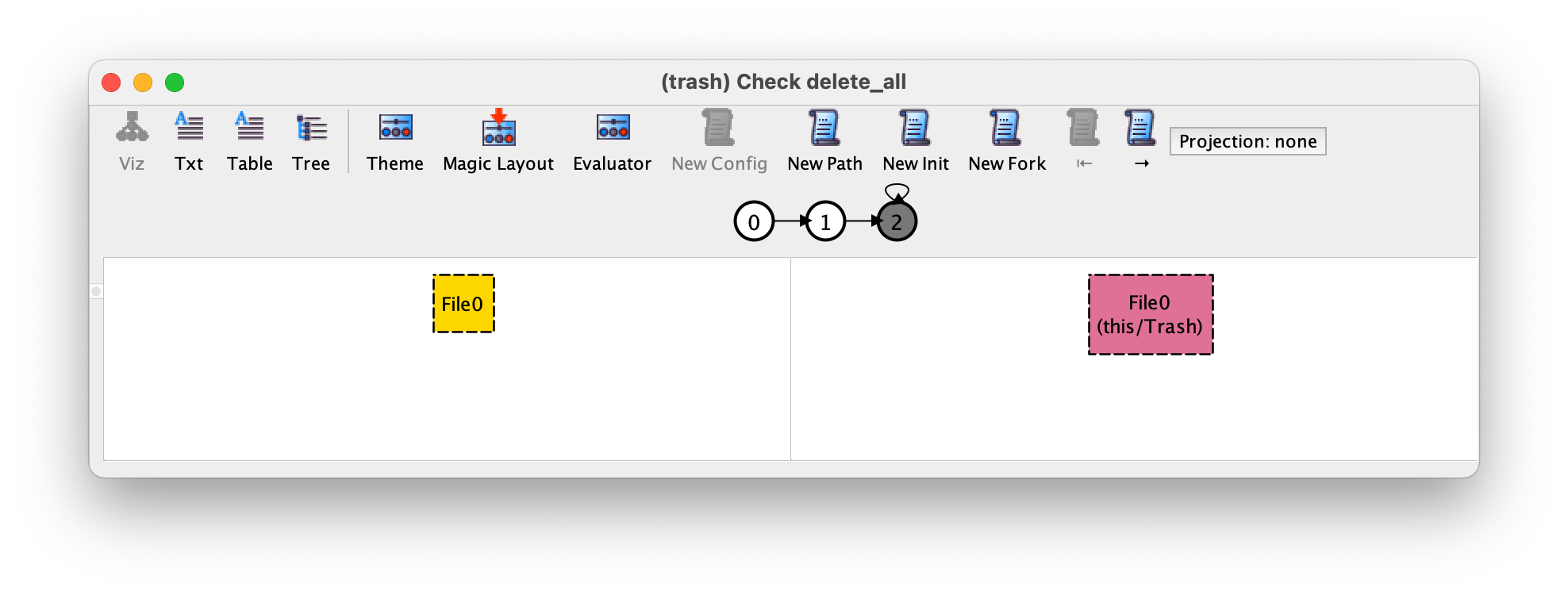
注意,这与我们运行 no_files 命令时得到的实例完全相同。乍看之下,这个跟踪并不像一个有效的反例,因为在删除了唯一存在的文件并清空了垃圾桶之后,文件系统仍然永远是空的。这种情况下的问题是,我们对属性的规范是有问题的(而不是对系统的规范,希望它仍然是正确的)。时间运算符的语义 always 要求随后的公式在公式被评估的状态下也成立,所以在上面的规范中,我们实际上是要求文件系统在发生空事件的同一状态下也是空的。这不是我们想要的:相反,我们应该要求文件系统永远是空的,但只在空事件发生后的(后)状态开始。我们可以通过在最内层的 always 之前添加一个 after 操作符来修复我们对该属性的规范。
assert delete_all {
always ((Trash = File and empty) implies after always no File)
}
现在该 check 命令不再产生反例,我们可以得出结论,我们的 Trash 组件设计很可能满足这两个属性!
![[Netty源码] ByteBufAllocator内存管理器相关问题 (十一)](https://img-blog.csdnimg.cn/b8146c9d0f284aa68618e3deb89c4290.png)