typescript 八叉树的简单实现

news2025/1/20 13:26:46

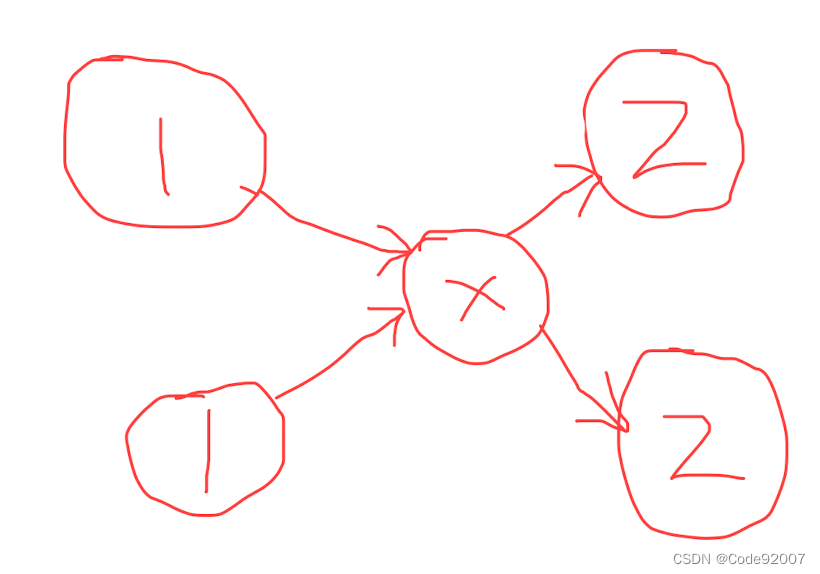
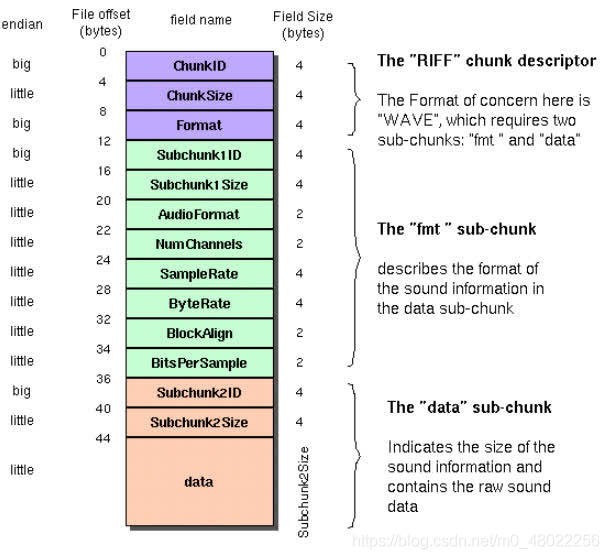
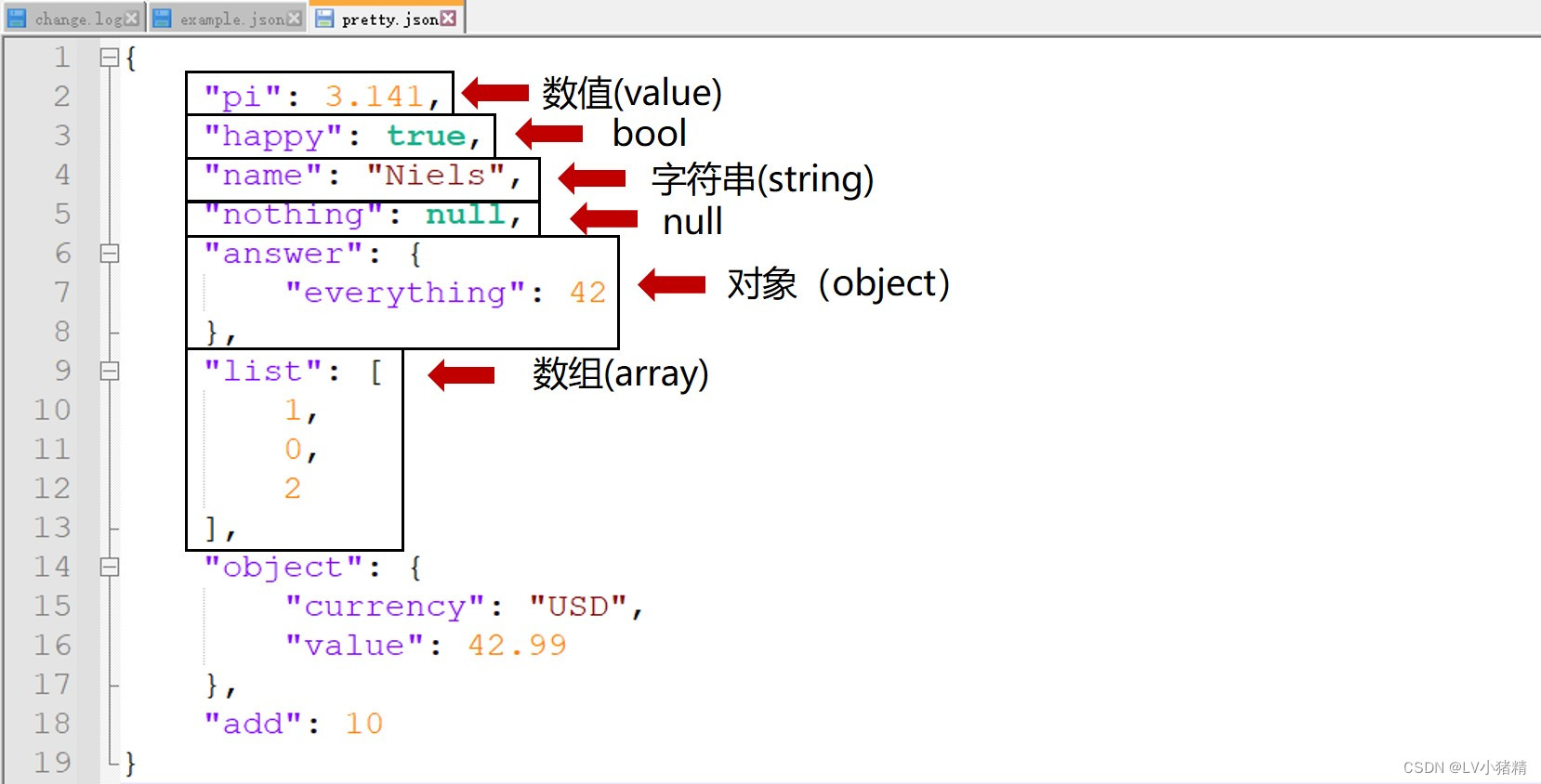
查了一些文章，准备自己用typescript写一个简单的八叉树场景管理。

所谓的简单，就是所有元素都是边长为1的立方体。

元素类和树节点类

//元素类，因为都是边长为1的立方体，所以就用cube命名
export class CubeData {
  public readonly position: Vec3 = new Vec3();
}

export class OcTreeNode {
  constructor(centerPosition: Vec3) {
    this.centerPosition.set(centerPosition);
  }
  centerPosition: Vec3 = new Vec3();//中心坐标
  children: OcTreeNode[] = [];//包含的子节点
  items: CubeData[] = [];//包含的元素数组
  sideLength = 0;//边长
  level = 0;//节点深度
}

其中Vec3为三维向量类，这里主要用来存储坐标。

判断元素是否和节点相交

需要x，y，z三个轴向的中心距离小于半边长之和。

即：

const isXIn = Math.abs(item.position.x - ocTree.centerPosition.x) < intersectDistance;
const isYIn = Math.abs(item.position.y - ocTree.centerPosition.y) < intersectDistance;
const isZIn = Math.abs(item.position.z - ocTree.centerPosition.z) < intersectDistance;
if (isXIn && isYIn && isZIn) {
//相交，则推入元素数组
   ocTree.items.push(item);
}

八叉树划分

进行围绕该节点的八个方向进行划分，划分的节点坐标基数是：

    [[1, 1, 1],
    [1, 1, -1],
    [1, -1, 1],
    [1, -1, -1],
    [-1, 1, 1],
    [-1, 1, -1],
    [-1, -1, 1],
    [-1, -1, -1]]

这些数据是基数，划分的节点的坐标应该是基数*变成的四分之一然后加上该节点的中心坐标。

然后，对包含元素大于1个的节点进行划分，直至最后划分到边长为1的节点。

    if (ocTree.items.length > 1 && ocTree.sideLength > 1) {
      for (let i = 0; i < APPConfig.ocTreeChildrenOffsetArray.length; i++) {
        const [x, y, z] = APPConfig.ocTreeChildrenOffsetArray[i];
        this.toolVec
          .set(x, y, z)
          .multiplyScalar(ocTree.sideLength / 4)
          .add(ocTree.centerPosition);
        const childOcTree = new OcTreeNode(this.toolVec);
        childOcTree.level = ocTree.level + 1;
        childOcTree.sideLength = ocTree.sideLength / 2;
        ocTree.children.push(childOcTree);
        this.initOcTree(childOcTree, ocTree.items);
      }
    }

为了避免在边长为1的节点里出现两个位置一样的元素，然后进行无意义划分，需要限制一下，不能对边长为1的节点进行划分。