题目
n*m(2<=n,m<=1e6,n*m<=1e6)的矩阵,
第i行第j列元素a[i][j](0<=a[i][j]<=n*m)
对于值为0的元素,你可以将其赋值为任意正整数,
不同位置的0元素,可以被赋值成不同的正整数
然后,你可以执行以下操作若干次:
1. 选择行i和行j,对于k∈[1,m],交换a[i][k]和a[j][k]
2. 选择列i和列j,对于k∈[1,n],交换a[k][i]和a[k][j]
若干次操作后,问矩阵是否能满足以下条件:
- A1,1≤A1,2≤⋯≤A1,W≤A2,1≤A2,2≤⋯≤A2,W≤A3,1≤⋯≤AH,1≤AH,2≤⋯≤AH,W
即每一行行内非严格递增,且第i行的最大值不超过第i+1的最大值
思路来源
官方题解
题解
首先,0是可以被忽略的,假设在一个非严格递增序列中插入0,
则0总可以赋值成其相邻左侧,或相邻右侧的值,使得序列的非严格递增性质保持不变
然后,矩阵会有一个行限制和一个列限制
1. 行限制,记每一行的最小值和最大值(mn,mx),然后按mn排增序,
则排增序之后,第i项的mx需要小于等于第i+1项的mn
2. 列限制,行操作完之后,每次只能交换两列,若干次操作后,
相当于找到一个列号的排列,使得每一行内成非严格递增
对于同一行不同列内的两个值来说,若j1列的值v1<j2列的值v2,则列j1需要在列j2左侧
连一条边之后,相当于需要对m列确定一个拓扑序,
但如果对每一行暴力连边,一行内的边数最多是C(m,2)的,总数n*C(m,2),不能接受
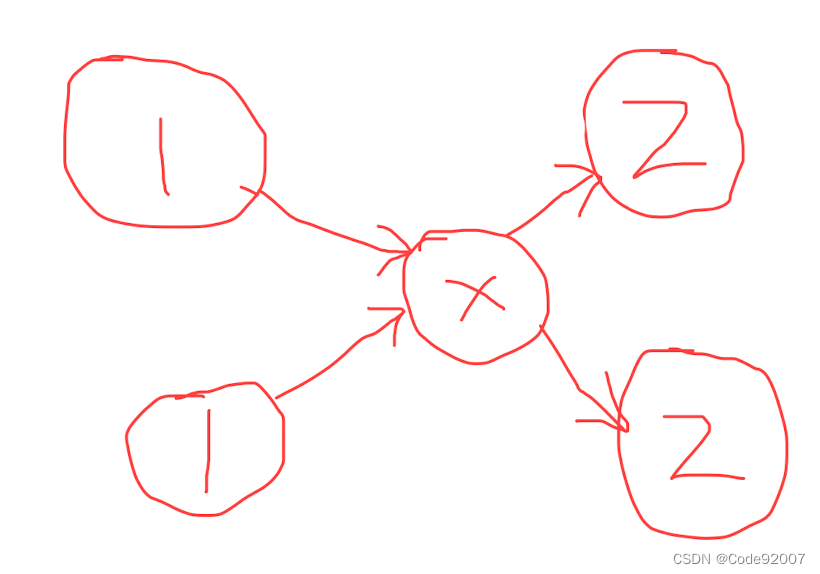
假设有两列的值是1,两列的值是2,考虑按如下图示,优化建边数
优化后,总的点数大致在2e6级别,而边数也大致在4e6级别,直接topo排序即可
图示
暴力连边
建虚点x连边
心得
虚点的做法,典中典,
之前只是在最短路中搞过虚点,实际这题说明,
需要连n*m条边的场合,都可以考虑尝试是不是能优化成n+m条边的
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> P;
const int N=2e6+10,INF=0x3f3f3f3f;
int n,m,in[N],tot,id;
P b[N],x[N];
vector<int>e[N];
queue<int>q;
void add(int u,int v){
e[u].push_back(v);
in[v]++;
}
int main(){
scanf("%d%d",&n,&m);
vector<vector<int>>a(n+1,vector<int>(m+1,0));
id=m;
for(int i=0;i<n;++i){
int c=0,cnt=0,mn=N,mx=0;
for(int j=0;j<m;++j){
scanf("%d",&a[i][j]);
cnt+=(!a[i][j]);
if(a[i][j]){
x[c++]=P(a[i][j],j);
mn=min(mn,a[i][j]);
mx=max(mx,a[i][j]);
}
}
if(cnt==m)continue;
b[tot++]=P(mn,mx);
sort(x,x+c);// 列限制
int las=-1;
for(int j=0;j<c;){
int k=j;
while(k+1<c && x[k+1].first==x[k].first)k++;
if(~las)for(int l=j;l<=k;++l)add(las,x[l].second);
las=id++;
for(int l=j;l<=k;++l)add(x[l].second,las);
j=k+1;
}
}
sort(b,b+tot);// 行限制
for(int i=1;i<tot;++i){
if(b[i-1].second>b[i].first){
cout<<"No"<<endl;
return 0;
}
}
for(int i=0;i<id;++i){
if(!in[i])q.push(i);
}
while(!q.empty()){
int u=q.front();q.pop();
id--;
for(auto &v:e[u]){
if(!(--in[v])){
q.push(v);
}
}
}
cout<<(!id?"Yes":"No")<<endl;
return 0;
}