数据结构与算法中的图
图的定义与术语
在线性结构之间,数据元素之间满足唯一的线性关系。每个数据元素(除第一个和最后一个外)只有一个****直接前趋和直接后继**
在树形结构中,数据元素之间有着明显的层次关系,并且每个数据元素只与上一层中的一个元素,(parenet node)及下一层中的多个元素(孩子节点)相关。
(线性结构、树形结构、图形结构)
在图形结构中,节点之间的关系是任意的,图中的任意两个数据元素之间都有可能相关。因此说,图是一种复杂的非线性结构。
图用 G = ( V , E ) G = (V,E) G=(V,E)表示,其中:
- V V V是顶点(vertex)的集合。
-
E
E
E是边(edge)的集合。
根据图中的边是否有方向,可以分为有向图和无向图。
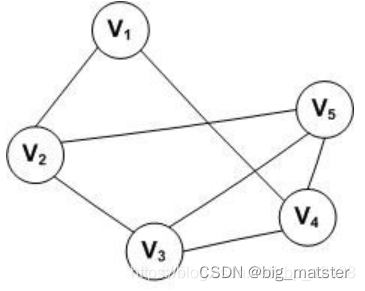
无向图
对于一个图,若每条边都是没有方向的。则称该图为无向图。
有向图
对于一个图,若每条边都是有方向的,则称该图为有向图。
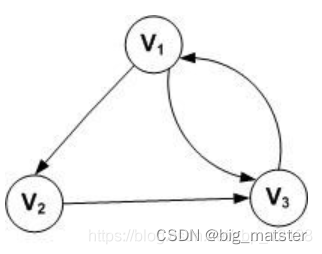
完全图
任意两个节点都有一条边相相连。
稀疏图
有很少边或弧的图,其指标为稀疏因子,若稀疏因子小于0.05,可认为是稀疏图。
密集图
有较多边或弧的图。
顶点的度
对于无向图,顶点的度表示以该顶点作为一个端点边的数目,比如上面的无向图,中顶点
V
3
V_3
V3的度
D
(
V
3
)
=
3
D(V_3) = 3
D(V3)=3
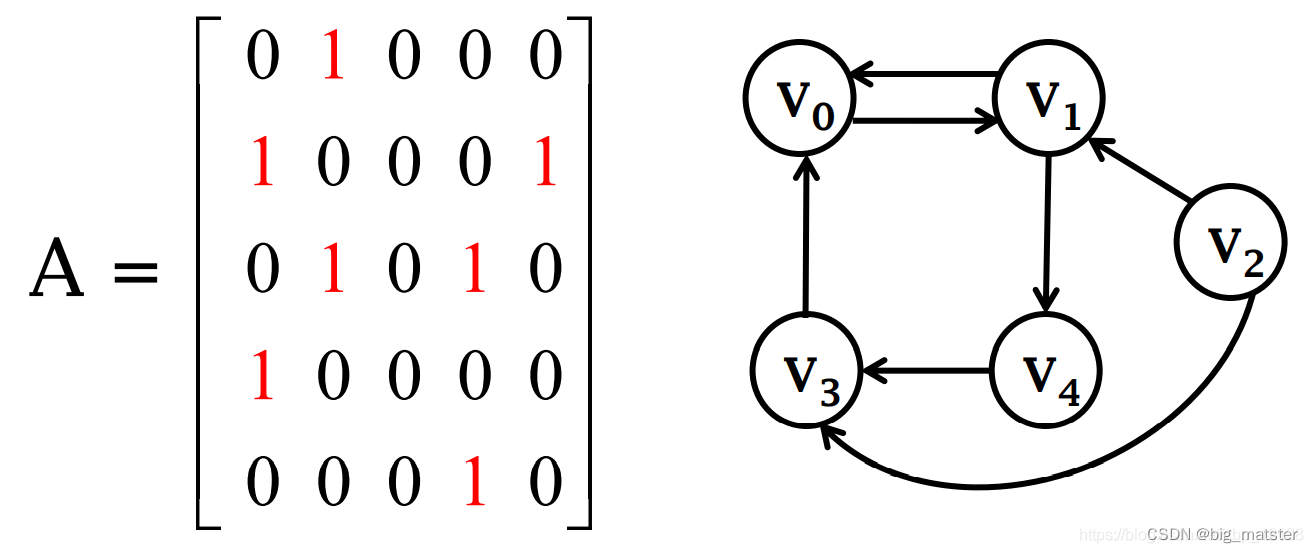
对于有向图,顶点的度分为入度和出度。某一顶点的度等于其入读和出度之和。
入度
入度表示以该顶点为终点的入边的数目。
出度
出度以该顶点为起点的出边的数目。
子图

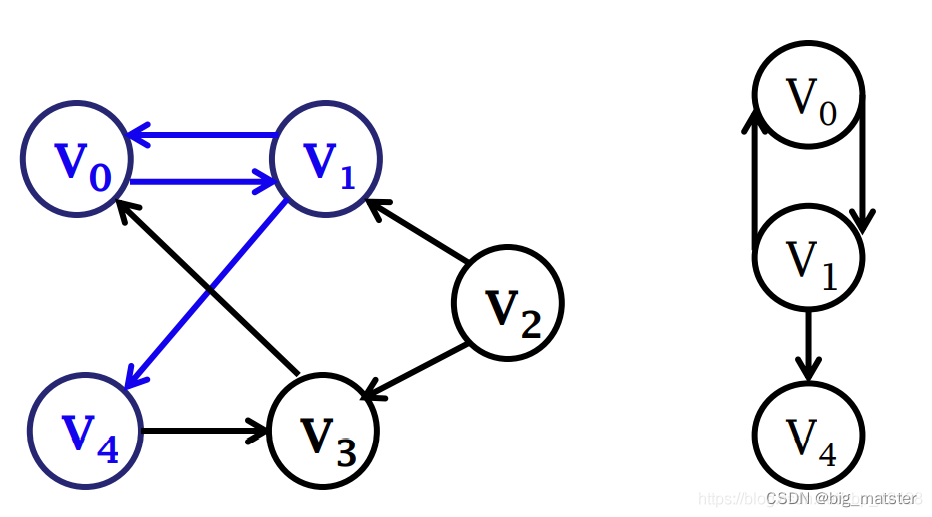
路径
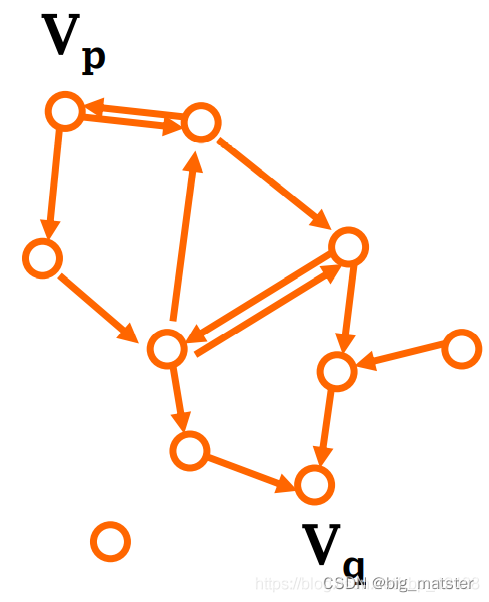

换句话说,路径都是从图上的一点出发,到图上另一点的方法。
从图上的一点出发,到图上另一点的方法可能不止一个,即可能有多个路径。
回路
回路也称为环,简单来说,回路是指一条路径的终点和起点为同一个顶点。
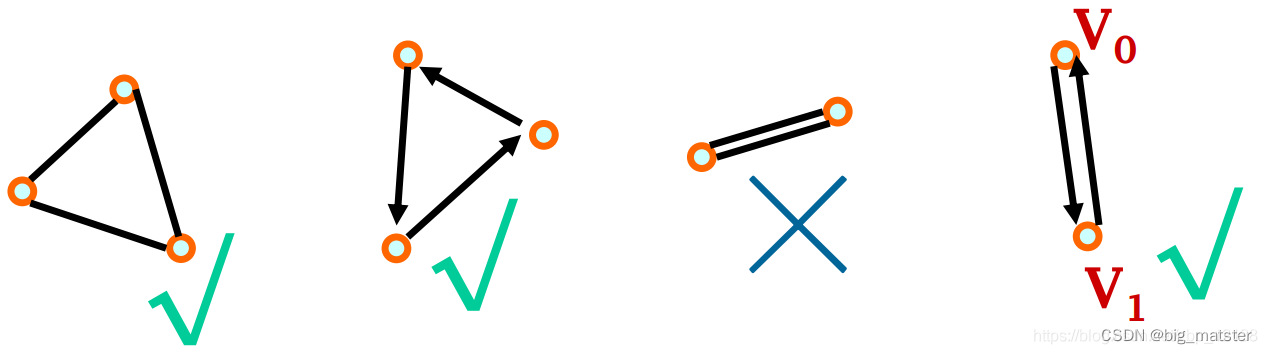
无向图中,如果两个节点之间有平行边,容易让人误看作环。
网络
带权重的连通图称为网。
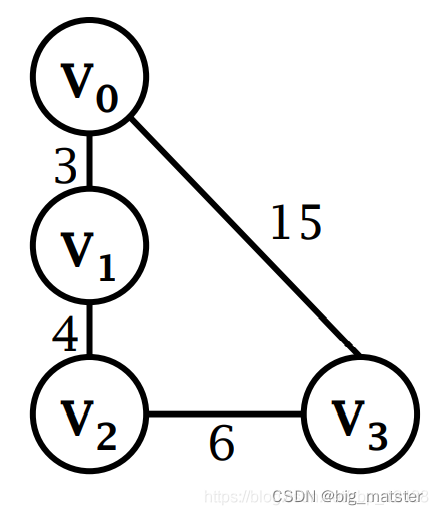
图的存储结构
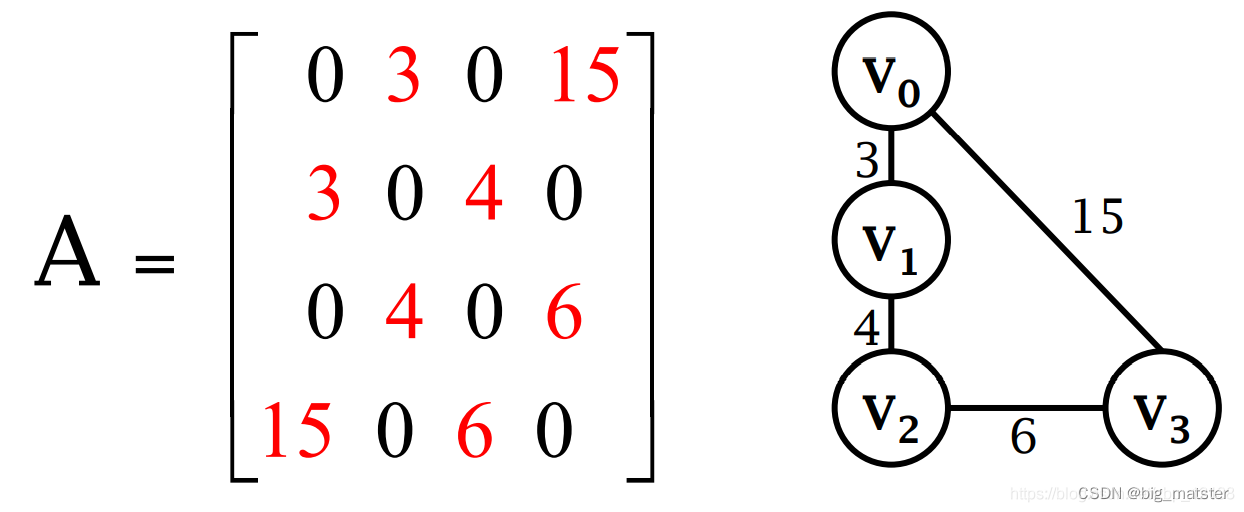
相邻矩阵
图的相邻矩阵,或邻接矩阵,表示顶点之间的邻接关系。即有没有边。
有向图的相邻矩阵
无向图的相邻矩阵
邻接表
对于稀疏图,可以采用邻接表存储法。
- 边较少,相邻矩阵就会出现大量的零元素
- 相邻矩阵的零元素就会耗费大量的存储空间和时间。
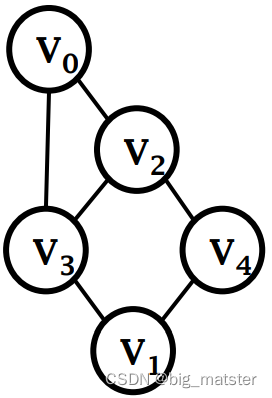
顶点和边的信息如下:
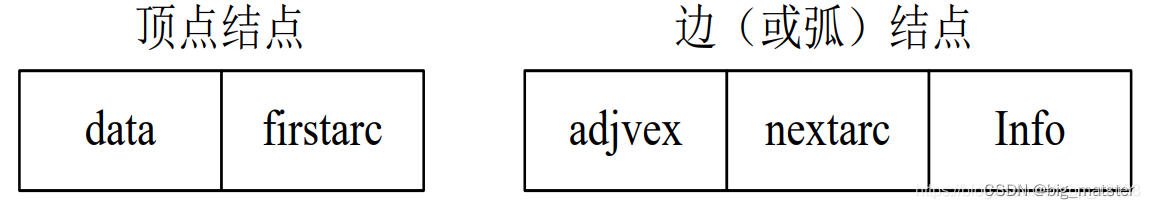
无向图的邻接表示
无向图同一条边,在邻接表中出现两次。
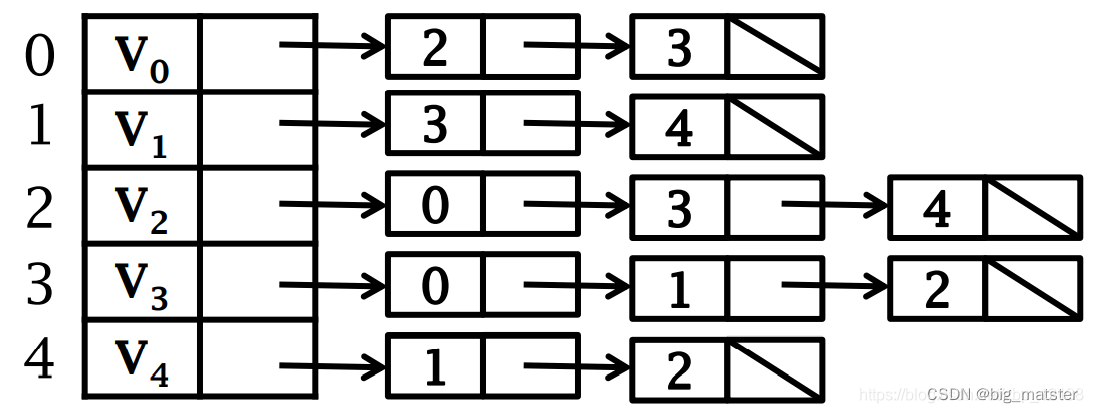
上面的图用邻接表可以表示:
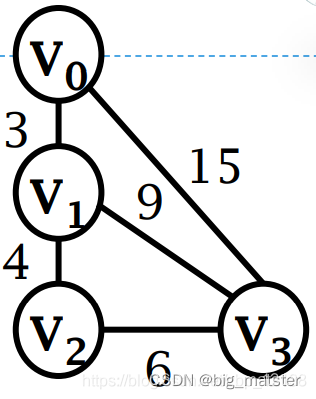
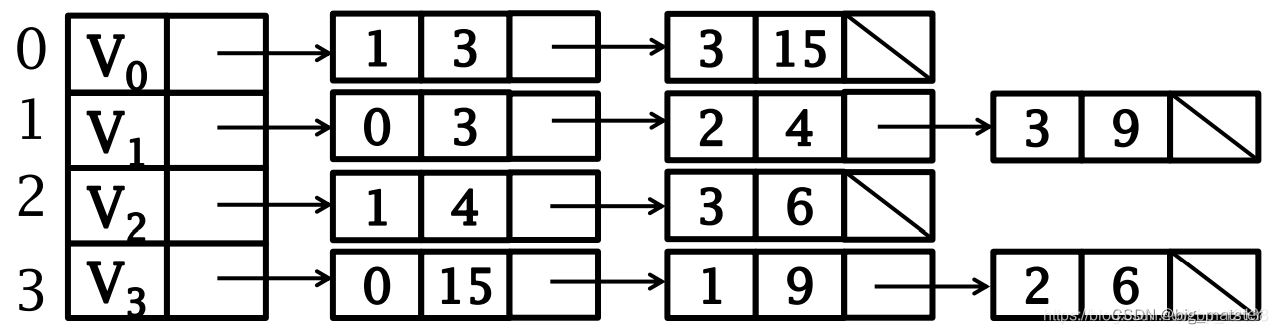
带权图的邻接表表示
有向图的邻接表(出边表)
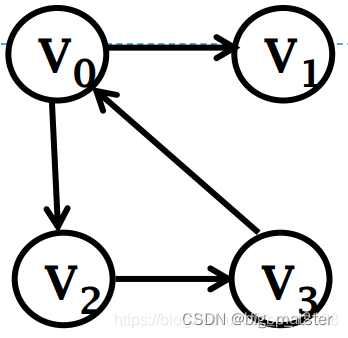
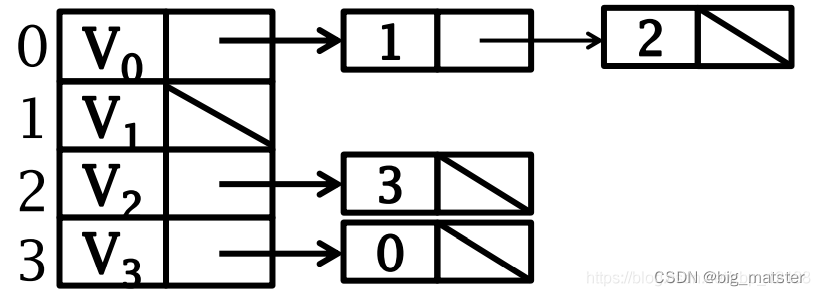
有向图逆邻接表(入边表)
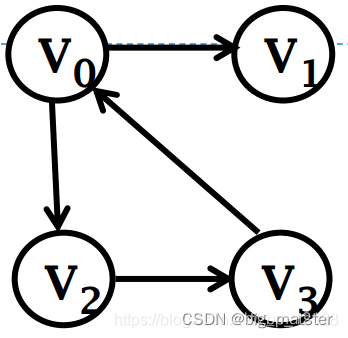
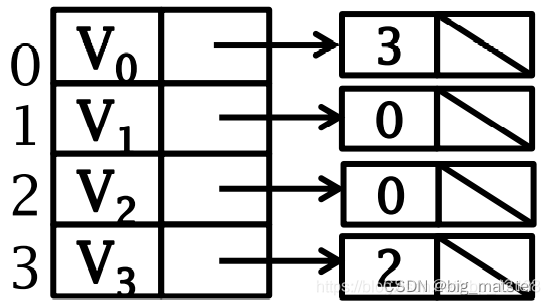
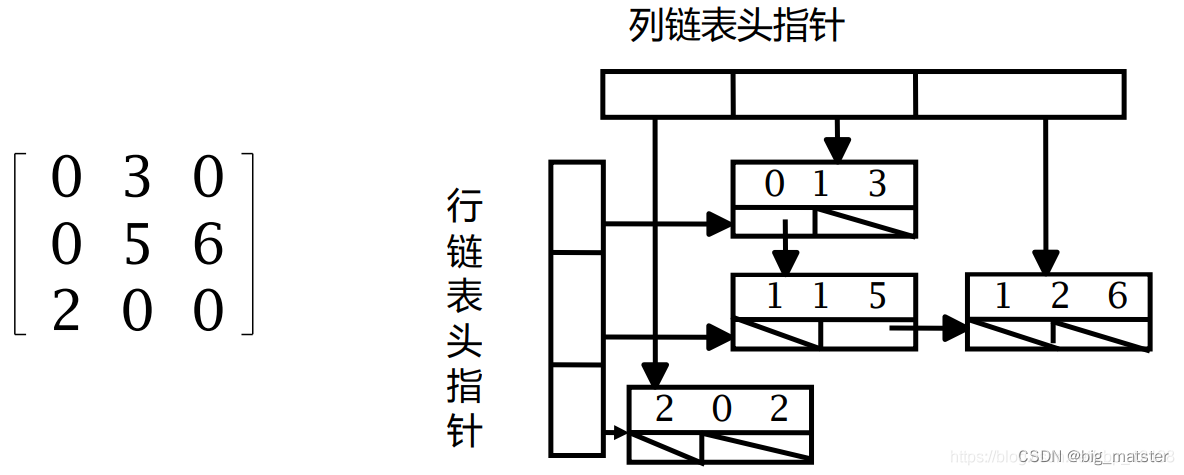
十字链表
十字链表可以看作是邻接表和逆邻接表的结合。
对应于有向图的每一条弧有一个条目:共有5个域:
- 头 : headvex
- 尾:tailvex
- 下一条共尾弧:tailnextarc
- 下一条共弧: headnextarc
- 弧权值等info域。
顶点表目有3个域组成:
- data 域
- firstinarc 第一条以该顶点为终点的弧
- firstoutarc 第一条以该顶点为始点的弧

十字链表有两组链表组成: - 行和列的指针序列
每个结点都包含两个指针: - 同一行的后继
- 同一列的后继
图的遍历
图的遍历是给出一个图 G G G和其中的任意一个顶点 V 0 V0 V0,从 V 0 V0 V0出发系统的访问 G G G中的所有的顶点,每个顶点访问而且只访问一次。
从一个顶点出发,试探性的访问其余顶点,同时必须考虑到下列情况:
- 从一个顶点出发,可能不能到达所有其他的顶点,如非连通图。
- 也有可能会陷入死循环,如存在回路的图。
一般情况下,可以为每个顶点保留一个标志位: - 算法开始时,所有顶点的标志位置零。
- 在遍历过程中,当某个顶点被访问时候,其标志位就会被标记为已访问。
深度优先遍历
深度优先搜索(简称DFS) 类似于树的先根次序遍历,尽可能先对纵深方向进行搜索:
** 选取一个未访问的点 v 0 v0 v0 作为源点
- 访问顶点$ v0$
- 递归地深搜遍历 $v0 $邻接到的其他顶点
- 重复上述过程直至从 $v0 $有路径可达的顶点都已被访问过
- 再选取其他未访问顶点作为源点做深搜,直到图的所有顶点都被访问过。
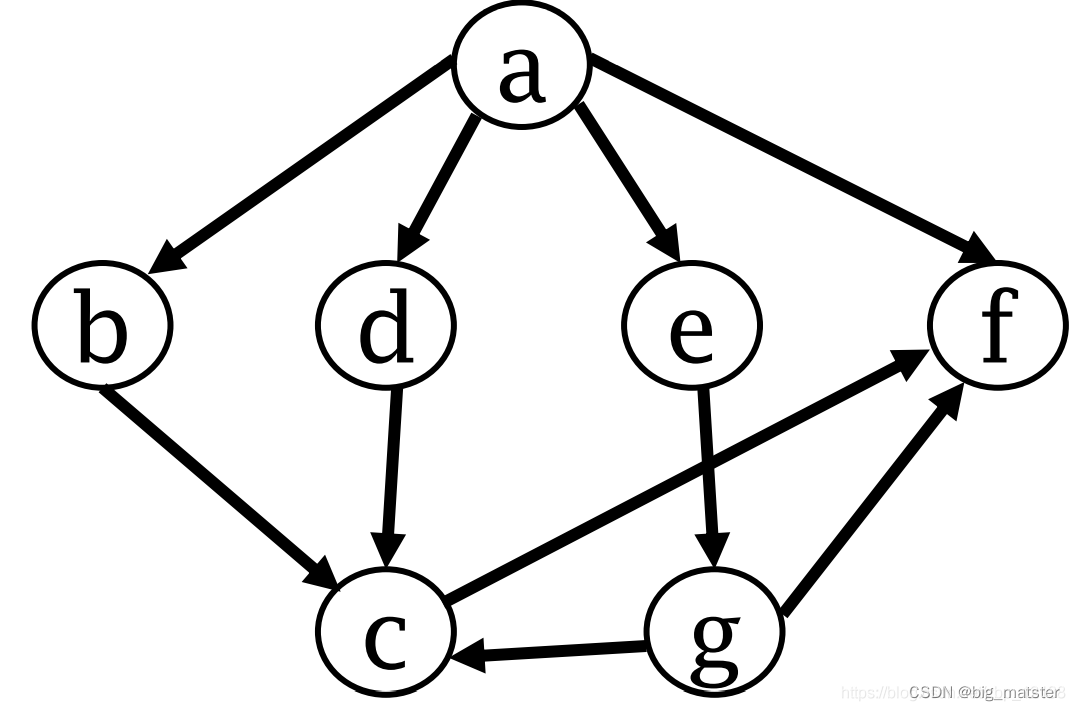
深度优先遍历的顺序是:
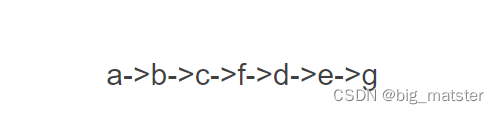
广度优先遍历
*** 广度优先搜搜**,其遍历过程是:
- 从图中的某个顶点 v0 出发
- 访问并标记了顶点 v0 之后
- 一层层横向搜索 v0 的所有邻接点
- 对这些邻接点一层层横向搜索,直至所有由 v0 有路径可达的顶点都已被访问过
- 再选取其他未访问顶点作为源点做广搜,直到所有点都被访问过
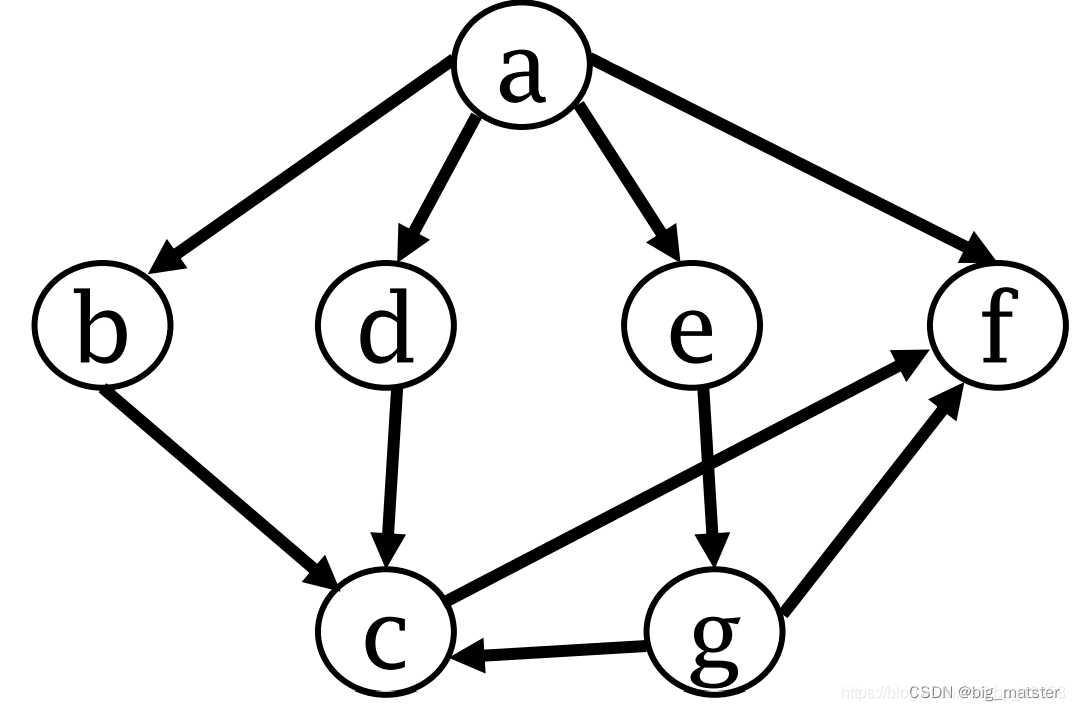
广度优先搜索的顺序是:

最短路径
单源最短路径

迪杰斯特拉算法

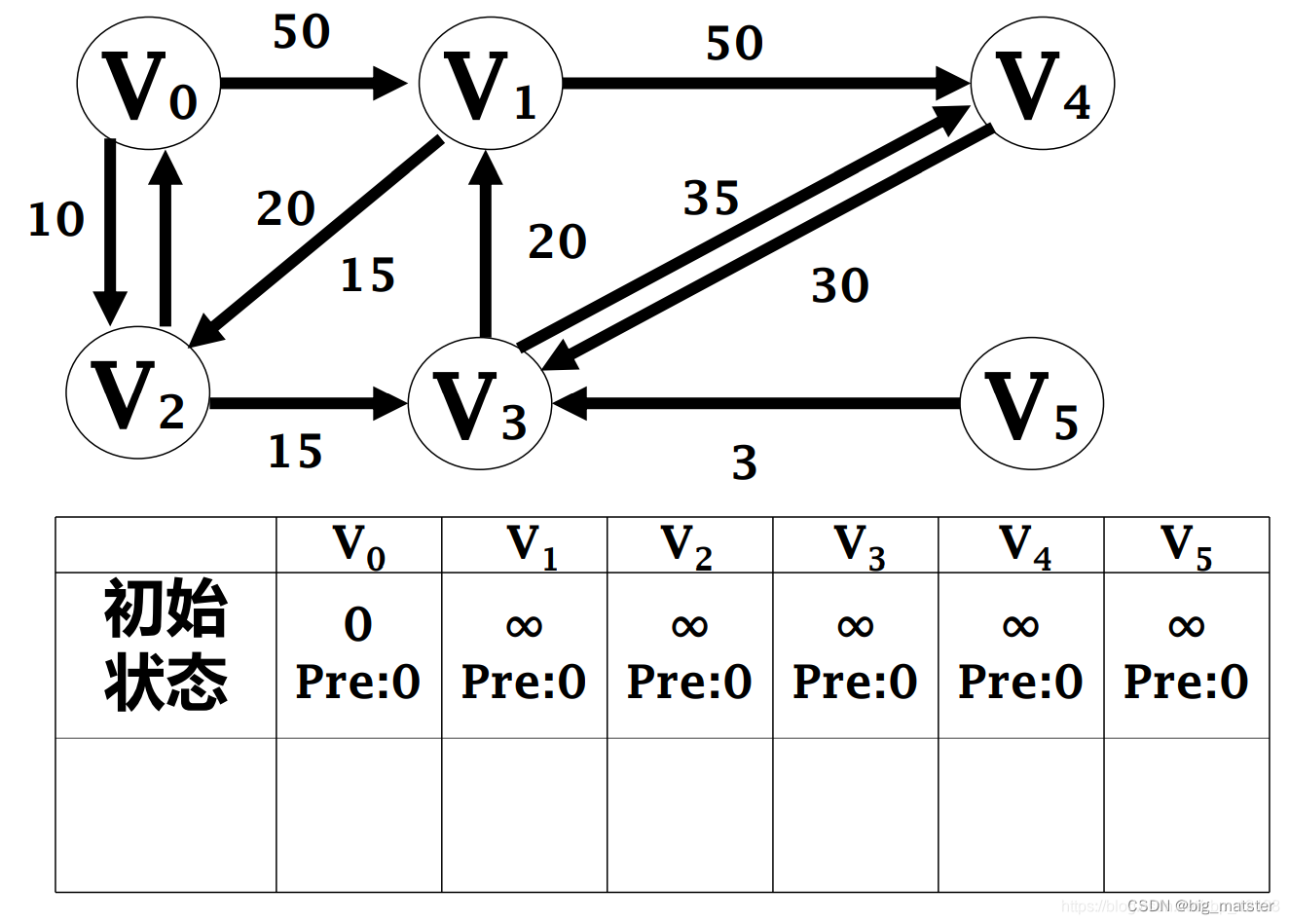
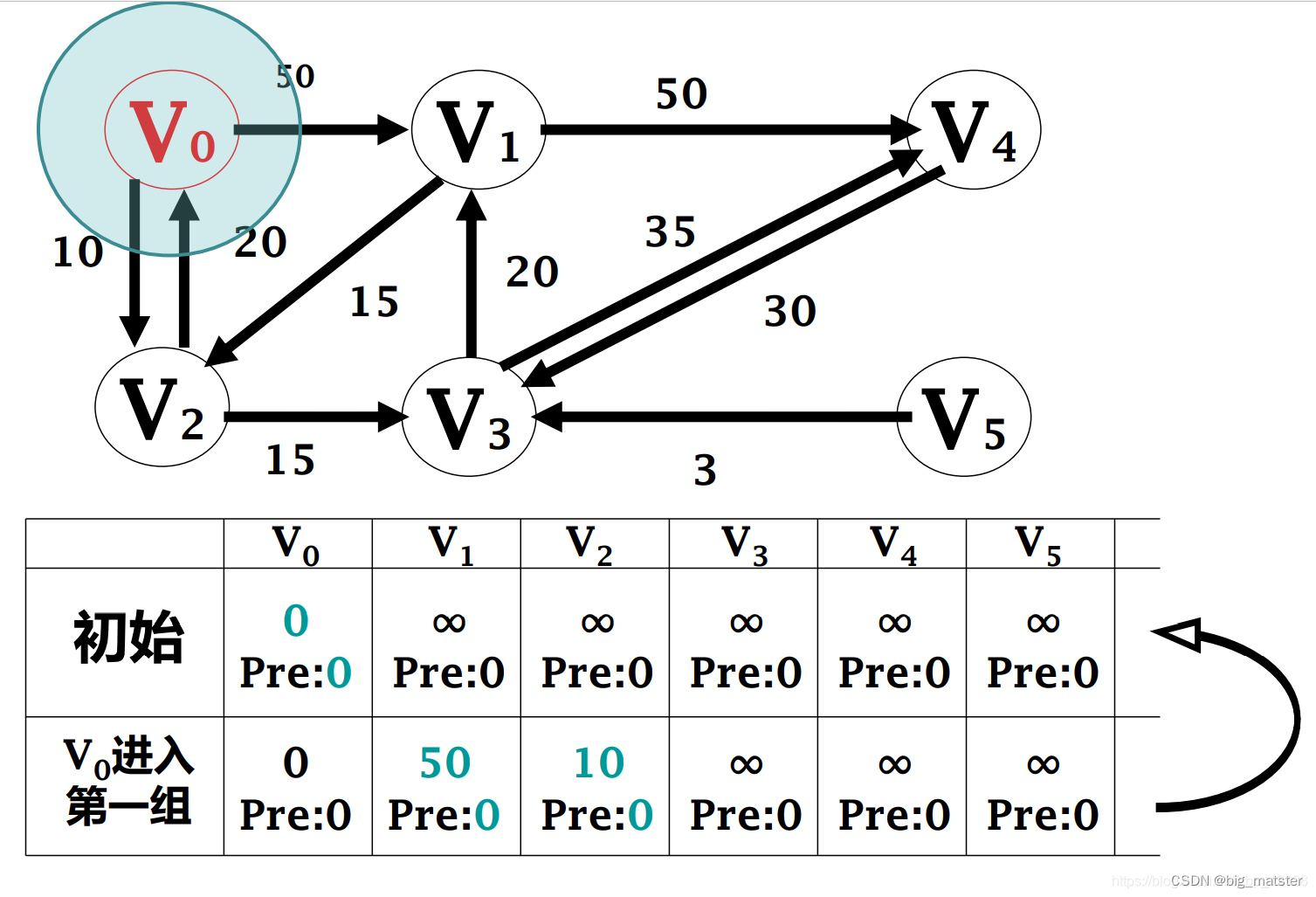
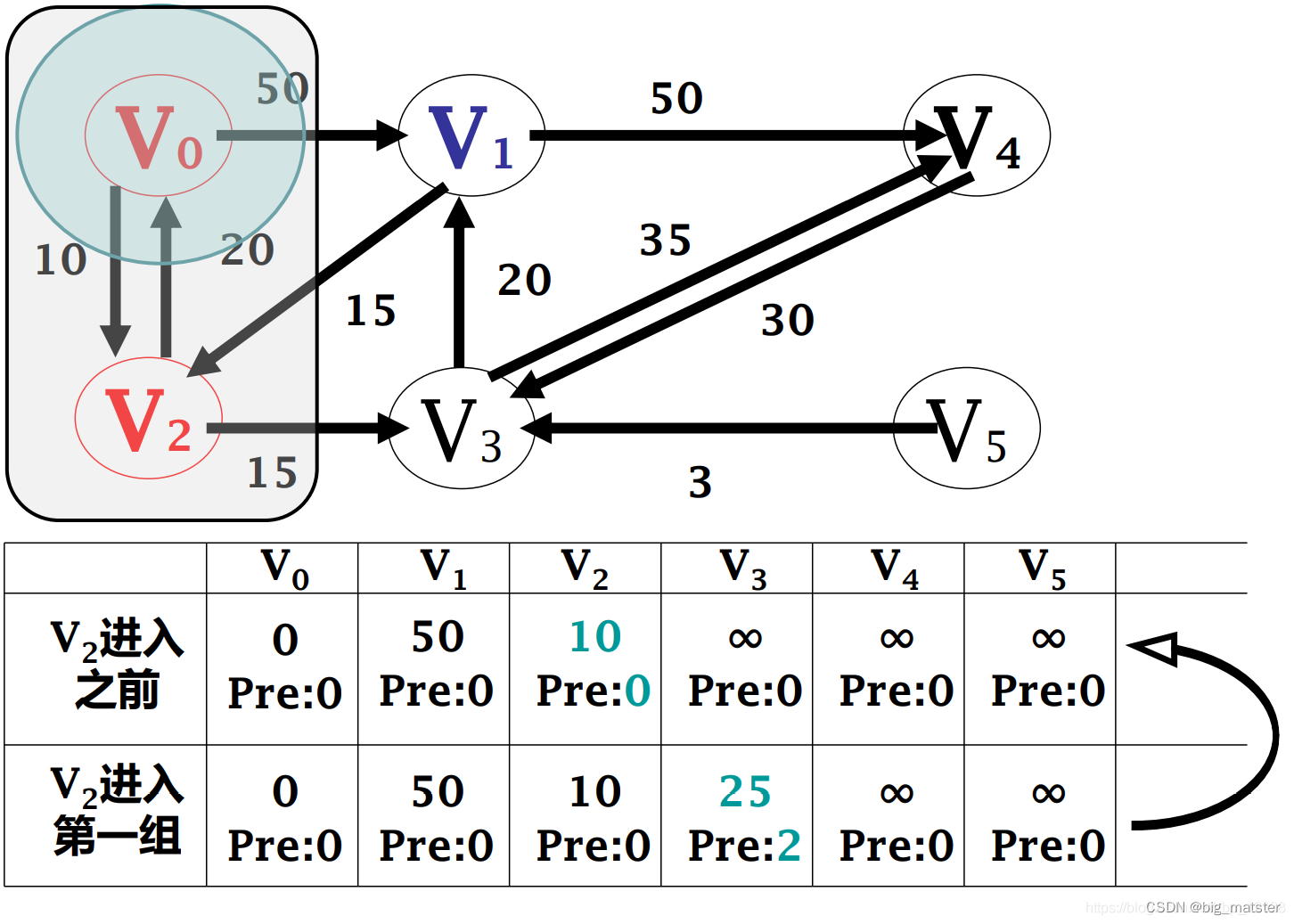
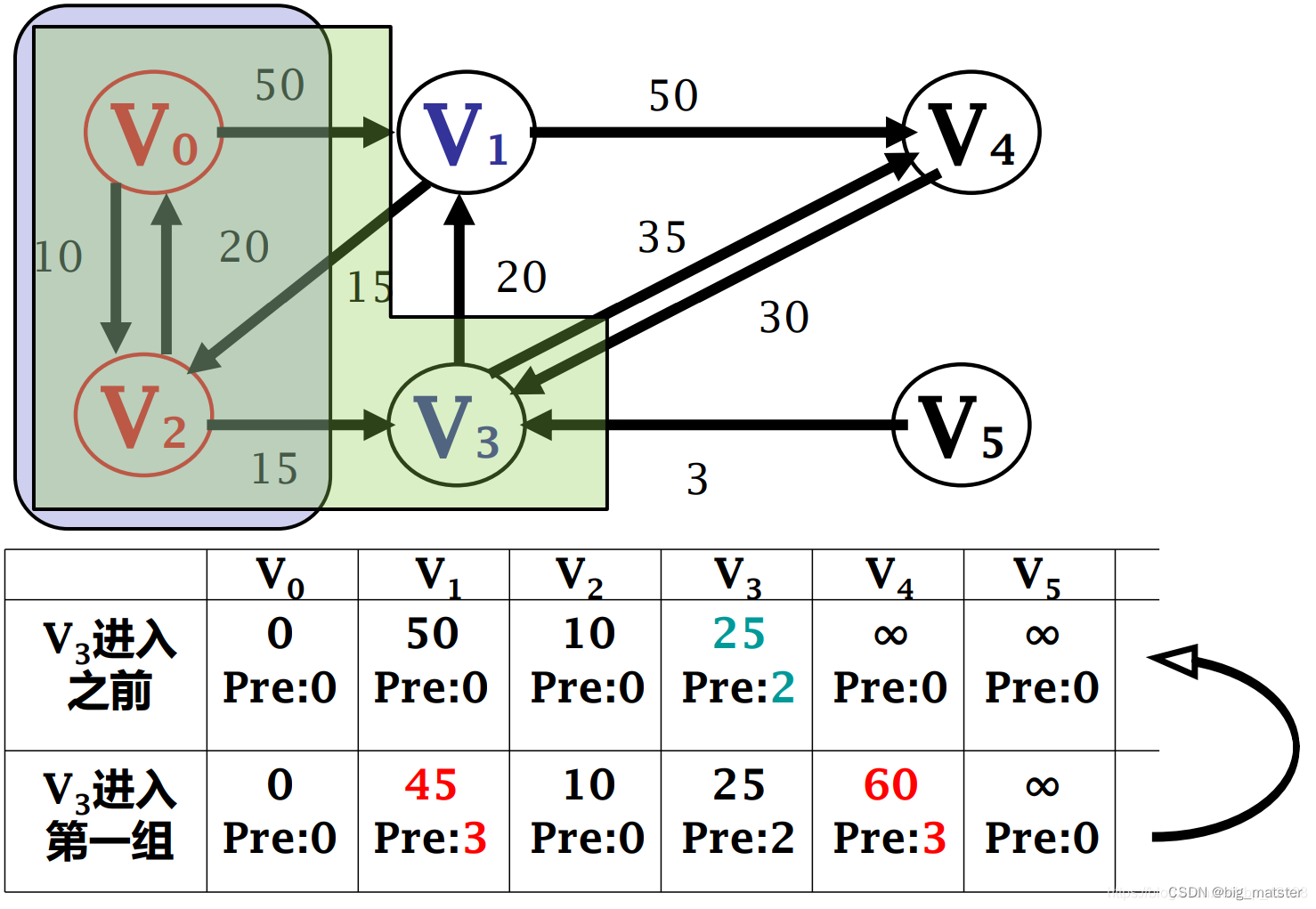
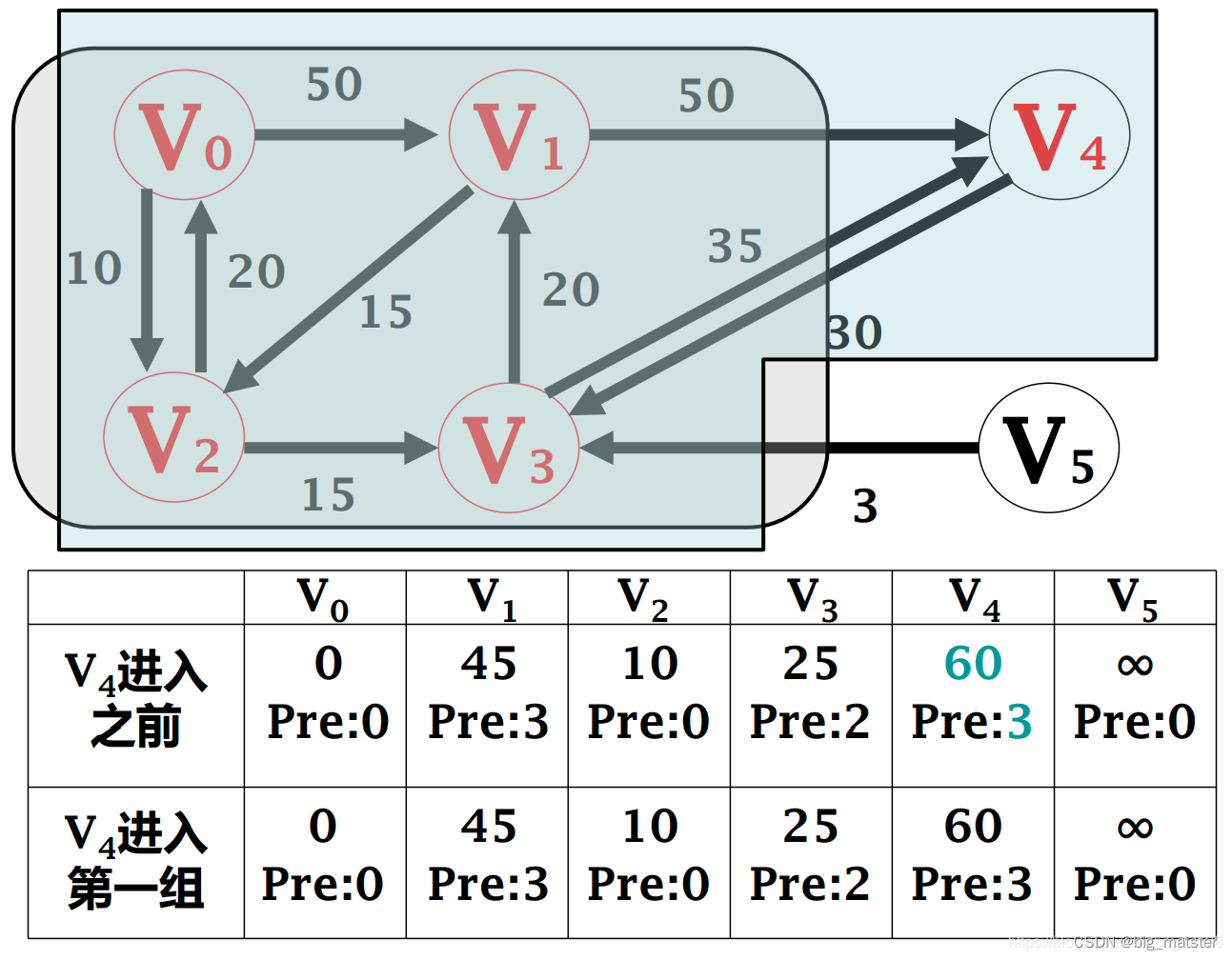
算法单源最短路径迭代过程:

该算法是贪心法, 不适用于负权值的情况,因为权直当做最小取进来后,不会返回去重新计算,即使不存在负的回路,也可能有在后面出现的负权值,从而导致整体计算错误。
每对结点间的最短路径
Floyd算法对每对结点之间的最短路径。
用邻接矩阵adj来表示带权有向 图。
基本思想

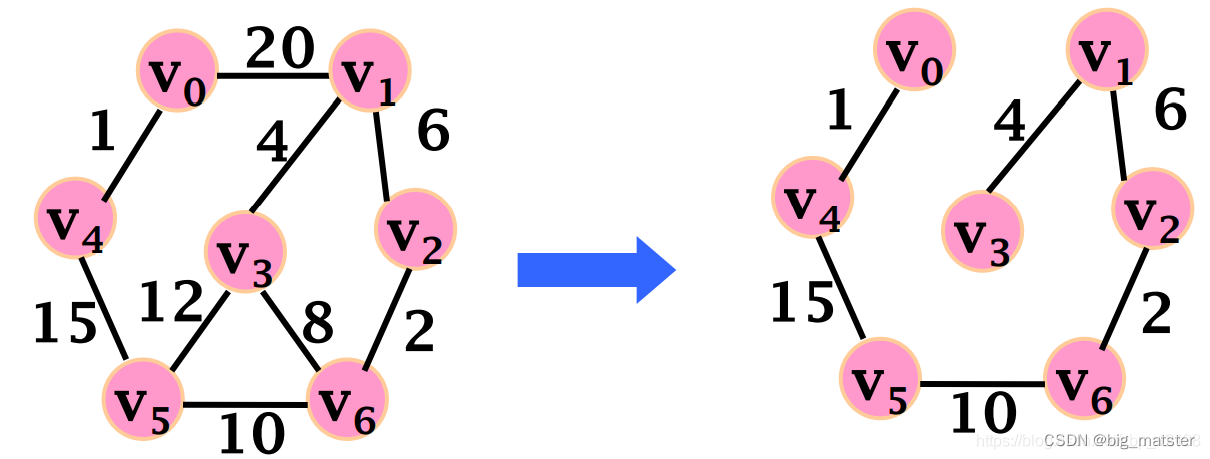
最小生成树
图 G G G的生成树是一颗包含所有顶点的树,树上的所有权值总和表示代价,那么在 G G G的所有的生成树中,代价最小的生成树,称为 G G G的最小生成树。
总结
不用太在意,慢慢的总结完整后,开始研究图结构及其存储,全部将其搞定都行啦的样子与打算。
不用太在意,其他的学习,要学会用可以用计算机自动计算出来‘
先助攻研读论文在说其他的样子域打算。