考点目录

文章目录

考点目录
复习准备
1. 数据挖掘的标准流程
2. 数据挖掘的主要功能
3. 数据探索的主要内容及其意义
- 数据质量分析
- - 1.异常值分析
  - 2.缺失值分析
- 数据特征分析
- - 1.分布分析
  - 6.相关性分析
4. 数据预处理的作用及其主要任务
5. 常见的噪声处理方法
6.常用的缺失值处理方法
7. 常用的数据变换方法
8. 常见的离群点检测方法
9. 数据的基本统计描述中常用的方法
10. 五数概括以及如何使用箱线图来识别列群点
11. apriori 算法实现的基本流程
- 1. 相关概念
- 2. 算法原理
12. FP-growth 算法实现的基本流程
- 1. 构建FP-tree
- 2. 通过条件模式基挖掘FP-tree
13.14. k-means DBSCAN算法请参考链接
15. ID3 算法的流程与步骤
- 基本概念
- 例题流程
16. C4.5 算法的流程与基本步骤
- 基本概念
- 例题流程
算法小结
17. 常见的集成方法及原理
18. 常见相似性度量
19. 模型评估的常用方法
20. 相关分析

复习准备

数据挖掘期末考试会给考纲，不同学校可能有所不同，大家看问题选取所需。另外有不正确的地方，或者遗漏的地方希望大家在评论区斧正和补充。

1. 数据挖掘的标准流程

商业理解：业务理解。
数据理解：认识数据、数据探索。
数据准备：数据选择和数据预处理。
建立模型：选择算法构建模型。
模型评估：评估模型是否满足商业应用需求，达成业务目标。
方案实施：部署。

2. 数据挖掘的主要功能

特征描述、鉴别、关联、分类、聚类、趋势和离群点分析。

3. 数据探索的主要内容及其意义

内容：数据质量分析和数据特征分析。

数据质量分析就是检测原始数据是否有脏数据。（异常值、缺失值、不一致的值）

数据质量分析

1.异常值分析

异常值分析就是检验数据是否含有不合理的数据（一般主要和实际业务考虑）
判断异常值方法主要有：

简单统计量分析
描述性统计describe（），能够查看哪些数据是不合理的，最常用的统计量有最大值，最小值，来判断这个变量是否超出了合理的范围。例如客户的最大年龄为200岁，该变量的取值存在异常。
3σ原则
如果数据服从正态分布，在3σ原则下，异常值被定义为一组测定值与平均值的偏差超过3倍标准差的值。
箱型图分析
箱型图提供了识别异常值的标准：小于Q1-1.5IQR或大于Q3+1.5IQR
Q1称为下四分位数
Q3称为上四分位数
IQR称为四分位数间距，也就是Q3-Q1之差

2.缺失值分析

包括记录中某个字段的信息缺失和记录的缺失。对于缺失值分析，要知道造成缺失值的原因，只有知道其原因，才能对症下药

造成缺失值的原因主要有俩种：

人为原因和非人为原因
人为原因：在录入数据时，可能认为该信息不重要或者忘记填写，造成信息遗漏
非人为原因：有些信息暂时无法获取或者获取的代价过大和某些信息属性值根本就不存在，例如一个未婚者的配偶姓名

数据特征分析

1.分布分析

主要揭示数据的分布特征和分布类型，可从定量数据和定性数据俩个角度考虑

对于定量数据，想要了解其分布类型是对称或者非对称的，可以通过绘制频率分布表，频率分布直方图进行直观分析

对于定性分类数据，可以用饼图和条形图直观显示分布情况

2.对比分析

3.统计量分析

4.周期性分析

5.贡献度分析（28法则）

6.相关性分析

绘制散点图或散点图矩阵（多个变量之间）
计算相关系数

个性相关系数：一般用于俩个连续性变量且服从正态分布

斯皮尔曼相关系数：一般用于不服从正态分布的变量，分类变量或等级变量之间的关联性

（3）系数检验

T检验

（4）判定系数

衡量回归方程对y的解释程度，R越大，说明拟合效果越好，说明X与之间的相关性越强

总结: 在得到原始数据后，一般要进行探索分析，数据质量分析要求我们要检测出数据是否存在异常值，和缺失值，数据特征分析要求我们通过频率分布分析，对比分析，帕累托图分析，周期性分析，相关性分析，对数据存在的某种规律和趋势预先了解。

4. 数据预处理的作用及其主要任务

作用：为了改善数据挖掘分析工作，减少时间，降低成本和提高质量。

主要任务

数据清洗： 填充缺失值，平滑噪声数据识别或删除异常值，纠正数据的不一致性。
数据集成： 针对多元异构数据，集成多个数据库、数据集、或文件。
数据规约：
维归约：数据压缩技术，特征选择和属性构造。
数值规约：抽样。
数据变换： 规范化、离散化、概念分层。

5. 常见的噪声处理方法

分箱

首先对数据进行排序并划分到(等频的)箱子中.
然后通过分箱的均值、中值、边界值进行平滑

回归

通过将数据拟合到回归函数中使其平滑.

离群点分析

聚类:检测并删除异常值.
统计学假设检验.
人工检测出可疑值.

6.常用的缺失值处理方法

忽略元组

进行监督学习，类标签缺失。
元组有多个缺失值。

人工填写缺失值：费时费力，不可取。

缺失值填充

使用常量填充，如分类变量新增一个类别 unknown。
使用属性的中心度量：中位数，众数，均值等。
使用元组同类所有样本属性的均值，中位数等。
推断最可能的值：回归，贝叶斯公式，决策树等。

7. 常用的数据变换方法

平滑：去除数据中的噪声。
属性构造：根据给定的属性构造新的属性。
聚合：汇总或聚集
规范化：按比例缩小到更小的范围内。最大-最小规范化，z-score规范化，小数定标。
离散化

8. 常见的离群点检测方法

分类

基于领域专家经验：有监督、半监督、无监督方法。
基于正常数据对异常值的假设(模型)：统计学、基于邻近性和聚类方法。

统计学方法

给定数据集中的对象是由随机过程（模型）产生的。
基本原理：学习一个拟合给定数据集的生成模型，然后识别该模型低概率区域中的对象，把他们作为离群点。
统计学方法的有效性在很大程度上取决于统计模型的假设在真实数据中是否成立。
常用方法：参数方法和非参数方法。

9. 数据的基本统计描述中常用的方法

PPT的内容

目的：为了更好的理解数据，中心趋势，变化和扩散。
数据分散性：中位数，最大值，最小值，分位数，离群点，方差等。
数值维度：对于排序区间，数据分布：多粒度分析；排序区间的箱线图或分位数分析。
计算度量的离散分析：映射测量成数值尺寸；对转换后的立方体进行箱线图或分位数分析。

参考书的内容

中心趋势度量：均值、中位数、众数。
度量数据散布：极差、四分位数、方差、标准差、四分位数极差。
数据的基本统计描述的图形显示。

注意：这两个地方表达的内容都是大同小异，根据老师的考纲走，可以找老师去问问这里，反正我周一就要问哦。

10. 五数概括以及如何使用箱线图来识别列群点

五数概括：从上至下，最大观测值、Q3、Q2、Q1、最小观测值。

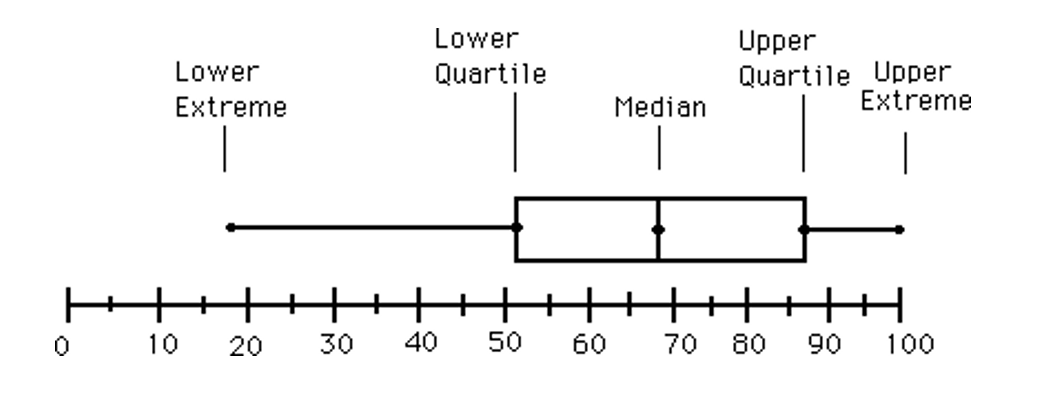
在这里插入图片描述

解释一下这图是怎么画的，四分位数：Q1,Q2,Q3。三条线把整个数据集分成四部分(中间砍四刀)。其次这里的最小观测值和最大观测值分别为：Q1 - 1.5 IQR,Q3 + 1.5 IQR. 其中 IQR 是四分位数极差 = Q3 - Q1 .注意：最大观测值和最小观测值不是固定的，根据数据集来定，但是一定在这个区间里面，超出了按照离群点来处理。

下面开始上硬菜了，嘿嘿嘿，算法来喽。

11. apriori 算法实现的基本流程

1. 相关概念

项集：项的集合成为项集。
k 项集：包含 k 个项的集合称为 k 项集，如：X = { $x_1,x_2,....,x_k$ }。
绝对支持度或支持度计数：指包含X项集的事务数。
相对支持度：项集 X 的绝对事务数与数据集事务总数的比值。
平繁项集：如果 X 的相对支持度大于预定义的最小支持度阈值，则项集 X 将频繁出现。

支持度s,反应规则的有用性。
$\rightarrow Y)=P(X \cup Y)=\operatorname{support}(X \cup Y)$

置信度c,反应规则的确定性。
$\rightarrow Y)=P(Y \mid X)=\frac{\operatorname{support}(X \cup Y)}{\operatorname{support}(X)}$

给出一个例题图：可能与你的概论学的有所差异，但是看着下面这张图，你就明白了。（60%，75%）代表的是（支持度，置信度）。

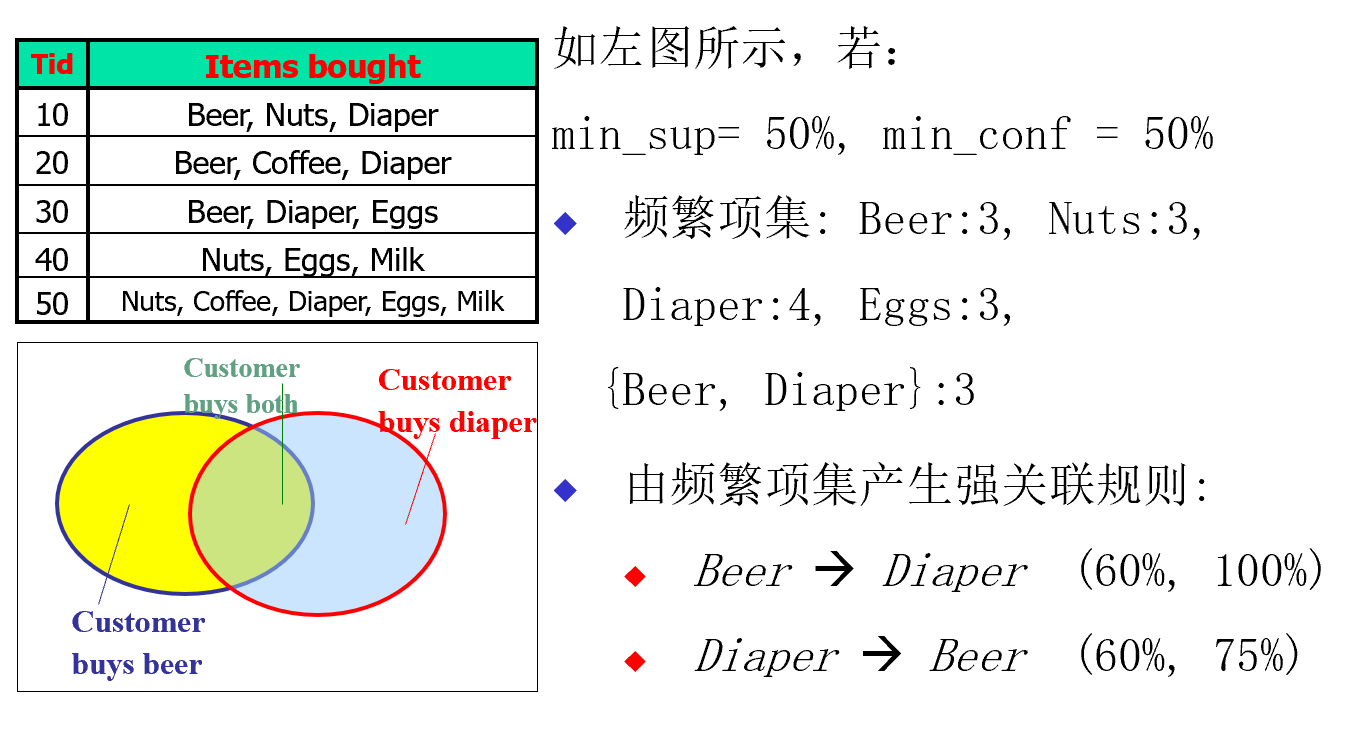
在这里插入图片描述

2. 算法原理

先验性质：频繁项集的所有非空子集也一定是频繁的。
反单调性：如果一个集合不能通过测试那么它的所有超集也不能通过相同的测试。
方法步骤;

首先扫描数据库获得频繁 1 项集。
从长度为 k 的频繁项集生成长度（k+1）的候选项集。
使用最小支持度来筛选候选集。
当不能生成频繁项集或者候选集时终止。

还是一张图解决问题：

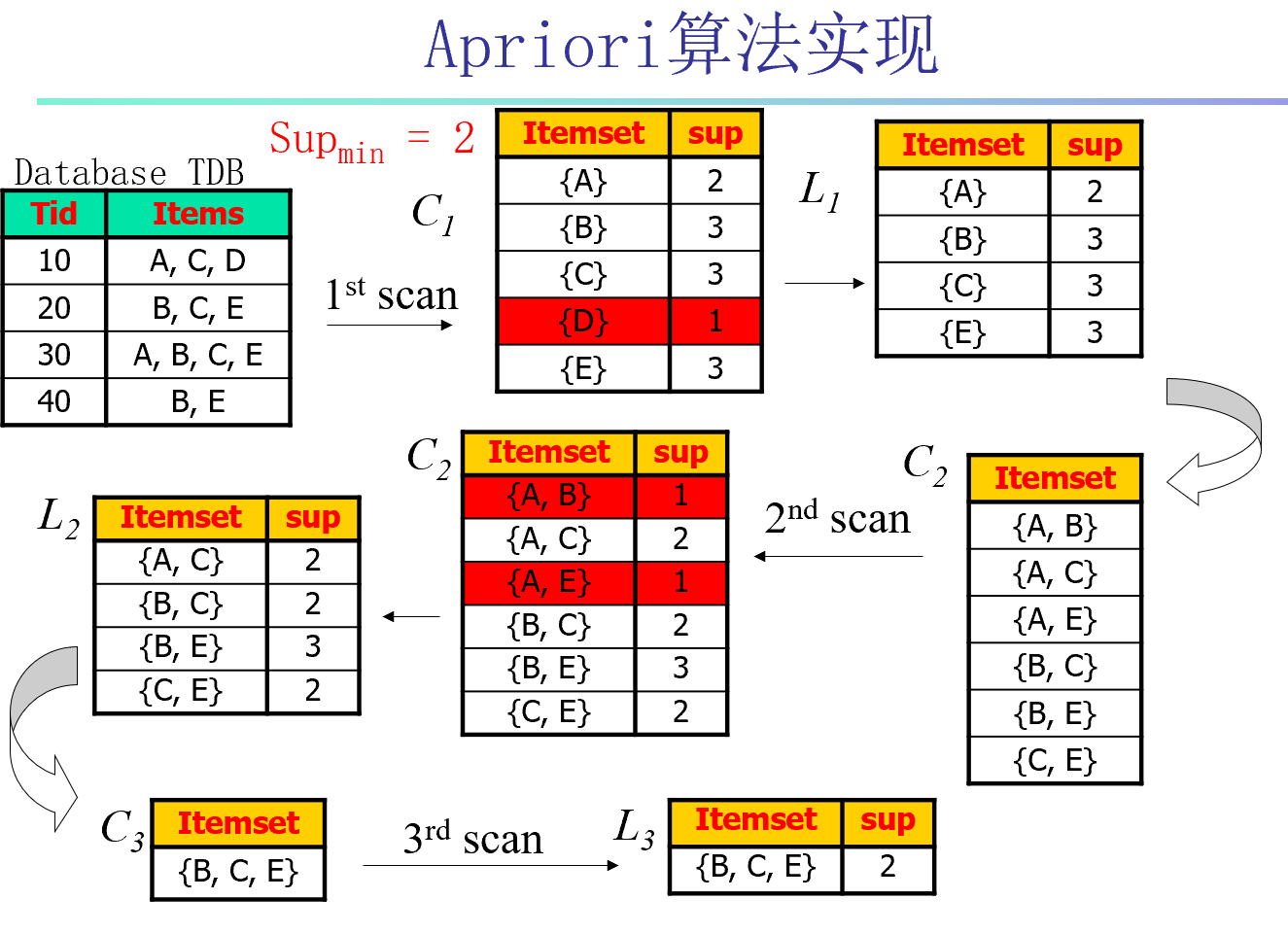
在这里插入图片描述

在这里我们第一要知道算法流程怎么用文字来描述，其次集合这张图懂得怎么使用这个算法。

12. FP-growth 算法实现的基本流程

Apriori 算法的瓶颈：广度优先，候选集生成和测试：通常会产生大量的候选集。
FP-growth:深度优先搜索，避免显示生成候选集。
主要理念：短模式到长模式，只是用局部频繁项。

1. 构建FP-tree

扫描数据库，查找 1 项集：和 Apriori 算法相同。
按频率降序排序形成频繁项列表。
再次扫描数据库构建 FP-tree.

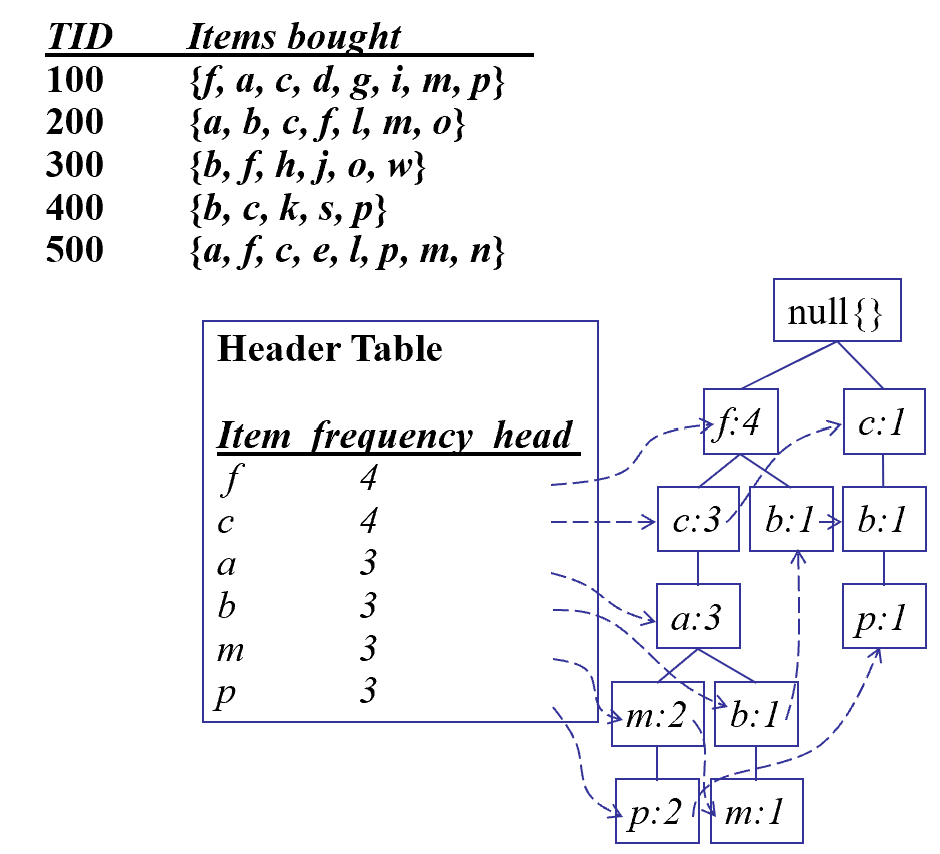
在这里插入图片描述

2. 通过条件模式基挖掘FP-tree

对每个条件模式基：

将每个项的计数累加到基数中。
为模式中的频繁项构建FP-tree.(每个项的支持度都要大于最小支持度的阈值)

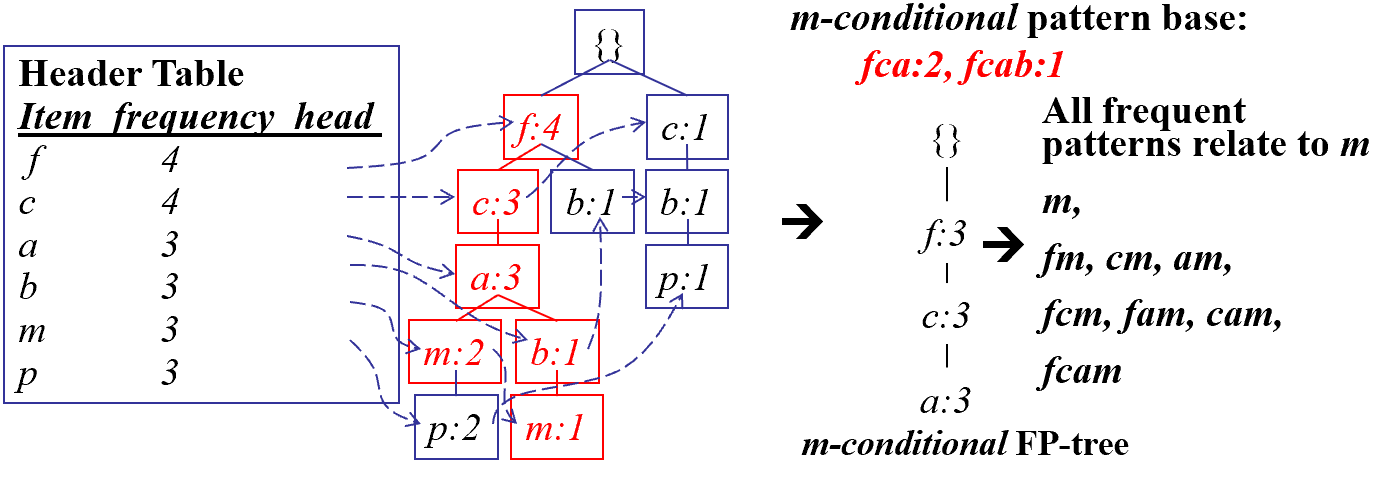
在这里插入图片描述

我们从最大频率的 f 开始，然后就去往下组合，fc 在事务集有多少，fa 又有多少，就这样链接关联下去就可建立一棵树。

在这里插入图片描述

看这张图来挖掘FP-tree,am 条件模式基就是 am 上面的父亲和祖宗，cm,cam 同样如此一直往上追溯到根节点。他的数目怎么算？就是等于开头字母在此路径上的数目，比如am,看到FP-tree中，a=3,m=2,那么它的条件模式基计数为 3.值得注意的是我们画FP-tree的根结点是空值哦！

13.14. k-means DBSCAN算法请参考链接

点击这里，当然可以去看看其他博主怎么说，欢迎battle！

15. ID3 算法的流程与步骤

ID3 算法主要选取信息增益来对数据集进行分割，下面来看一看具体怎么做的吧。

基本概念

选择信息增益最高的属性。
设 $P_i$ 为 D 中任意一个元组属于类 $C_i$ 的非零概率估计。
期望信息熵是数据集 D 中每条数据完成分类所需要的信息：
$\operatorname{Info}(D)=-\sum_{i=1}^{m} p_{i} \log _{2}\left(p_{i}\right)$
使用属性 A 将数据集 D 分成 V 个部分后还需要多少信息完成数据集分类，值越小，分区纯度越高。
$\operatorname{Info}_{A}(D)=\sum_{j=1}^{v} \frac{\left|D_{j}\right|}{|D|} \times \operatorname{Info}\left(D_{j}\right)$
其中 V 是数据分区数， $D_j|$ 表示第 j 个分区的长度， $\frac{|D_j|}{|D|}$ 表示第 j 个分区的权重。
信息增益：通过属性 A 上的分支获得的信息如下：
$\operatorname{Gain}(A)=\operatorname{Info}(D)-\operatorname{Info}_{A}(D)$

下面我们通过一道例题来巩固一下：

例题流程

下表是一些带有标记类的训练集 D, 训练集的列是一些特征，表中最后一列是类标号，就是需要我们分类的。

在这里插入图片描述

计算信息熵： $\operatorname{Infor}(D)=-\frac{9}{15} \times \log _{2} \frac{9}{15}-\frac{6}{15} \times \log _{2} \frac{6}{15}=0.971$
计算按照每个特征进行划分的信息熵 Info $_A$ (D),假设我们用 A,B,C,E分别代表学历、婚否、是否有车、收入水平。分别计算出每个属性分类的信息熵。
$\begin{aligned} \operatorname{Info_A}(D) &=\frac{5}{15} \times\left(-\frac{2}{5} \log _{2} \frac{2}{5}-\frac{3}{5} \log _{2} \frac{3}{5}\right) \\ &+\frac{5}{15} \times\left(-\frac{3}{5} \log _{2} \frac{3}{5}-\frac{2}{5} \log _{2} \frac{2}{5}\right) \\ &+\frac{5}{15} \times\left(-\frac{4}{5} \log _{2} \frac{4}{5}-\frac{1}{5} \log _{2} \frac{1}{5}\right)=0.888 \end{aligned}$
同理：
$\begin{aligned} & \operatorname{Info_B}(D)=\frac{10}{15} \times\left(-\frac{6}{10} \log _{2} \frac{6}{10}-\frac{4}{10} \log _{2} \frac{4}{10}\right)+\frac{5}{15} \times \left(-\frac{5}{5} \log _{2} \frac{5}{5}\right)=0.647 \\ & \operatorname{Info_C}(D) = \frac{9}{15} \times\left(-\frac{6}{9} \log _{2} \frac{6}{9}-\frac{3}{9} \log _{2} \frac{3}{9}\right)+\frac{6}{15} \times\left(-\frac{6}{6} \log _{2} \frac{6}{6}\right)=0.951 \\ & \operatorname{Info}_{E}(D) = \frac{5}{15} \times\left(-\frac{4}{5} \log _{2} \frac{4}{5}-\frac{1}{5} \log _{2} \frac{1}{5}\right)+\frac{6}{15} \times\left(-\frac{2}{6} \log _{2} \frac{2}{6}-\frac{4}{6} \log _{2} \frac{4}{6}\right) + \frac{4}{15} \times\left(-\frac{4}{4} \log _{2} \frac{4}{4}\right)=0.608 \end{aligned}$

3.计算信息增益：
$\begin{array}{l} \operatorname{Gain}_{A}(D)=\operatorname{Info}(D)-\operatorname{Info} _{A}(D)=0.083 \\ \operatorname{Gain}_B(D)=\operatorname{Info}(D)-\operatorname{Info} _{B}(D)=0.324 \\ \operatorname{Gain_C}(D)=\operatorname{Info}(D)-\operatorname{Info}_{C}(D)=0.020 \\ \operatorname{Gain}_{E}(D)=\operatorname{Info} (D)-\operatorname{Info}_{E}(D)=0.363 \end{array}$

选择信息增益最大 E(收入水平) 作为结点进行分割，纯的块不管，不纯的我们继续重复1-3，此时应该把纯的给剔除掉（叶子节点），缩小数据集。直到所有类别都分好类为止。

16. C4.5 算法的流程与基本步骤

C4.5算法在构建决策树的时候，分类属性选择的是具有最大信息增益率 的特征，这样通过分裂属性的信息，一定程度上避免了由于特征太分散而造成的误差。流程与 ID3 相似。
C4.5 连续值处理：

根据连续属性进行排序，用不同的值对数据集进行动态分割，把数据集分成两部分，一部分大于某值，一部分小于某值。
进行信息增益计算，最大值的那块作为最后划分。
假设属性 A 是连续值，必须确定 A 的最佳分裂点，其中分裂点是 A 上的阈值。将 A 的值按照递增排序，没对相邻值的中间可能作为分裂点。当 A 具有 n 个值时，需要计算 n-1 个划分。

基本概念

属性选择：信息增益会偏向多值属性。
C4.5 选择信息增益率（信息增益归一化），可以更好处理连续值。
$\operatorname{SplitInfo}_{A}(D)=-\sum_{j=1}^{v} \frac{\left|D_{j}\right|}{|D|} \times \log _{2}\left(\frac{\left|D_{j}\right|}{|D|}\right)$
信息增益率：
$\frac {Gain(A)}{\operatorname {SplitInfo}_A(D)}$

利用上图计算信息增益率：Gain(income) = 0.029
$\text { SplitInfo }{ }_{income}(D)=-\frac{4}{14} \times \log _{2}\left(\frac{4}{14}\right)-\frac{6}{14} \times \log _{2}\left(\frac{6}{14}\right)-\frac{4}{14} \times \log _{2}\left(\frac{4}{14}\right)=1.557$

$\operatorname{GainRatio}_ { income }=\frac{0.029}{1.557}=0.019$

例题流程

在这里插入图片描述

设 A,B,C,E 分别表示：年龄，吸烟史，有无家族病史，体重范围。

首先计算按照每个特征进行分裂的信息增益率，处理连续值：

在这里插入图片描述

我们可以在年龄为 44 处的地方断开。

计算各个特征分裂信息：
$\begin{array}{l} \operatorname{SplitInfo}_{A}(Z)=-\sum_{j=1}^{n} \frac{\left|Z_{j}\right|}{|Z|} \times \log _{2}\left(\frac{\left|Z_{j}\right|}{|Z|}\right)\\ \\=-\frac{7}{15} \times \log_{2} \frac{7}{15}-\frac{8}{15} \times \log _{2} \frac{8}{15}=0.997 \\ \\\operatorname { SplitInfo}_{B}(Z)=-\frac{9}{15} \times \log_{2} \frac{9}{15}-\frac{3}{15} \times \log _{2} \frac{3}{15}-\frac{3}{15} \times \log _{2} \frac{3}{15}=1.371 \\ \\\operatorname { SplitInfo}_{C}(Z)=-\frac{6}{15} \times \log_{2} \frac{6}{15}-\frac{9}{15} \times \log _{2} \frac{9}{15}=0.971 \\ \\\operatorname { SplitInfo}_{E}(Z)=-\frac{2}{15} \times \log _{2} \frac{2}{15}-\frac{2}{15} \times \log _{2} \frac{2}{15}-\frac{3}{15} \times \log _{2} \frac{3}{15}-\frac{6}{15} \times \log _{2} \frac{6}{15}-\frac{2}{15} \times \log _{2} \frac{2}{15}=2.156 \end{array}$
计算各属性的信息增益率：
$\begin{array}{l} g_{r}(Z, A)=\frac{g(Z \mid A)}{\operatorname{SplitInfo} _{A}(Z)}=\frac{\operatorname{Info}(Z)-\operatorname{Info} (Z \mid A)}{\operatorname{SplitInfo} _{A}(Z)}=\frac{0.997-0.566}{0.997}=0.432 \\ \\g_{r}(Z, B)=\frac{g(Z \mid B)}{\operatorname{SplitInfo} _{B}(Z)}=\frac{\operatorname{Info}(Z)-\operatorname{Info} (Z \mid B)}{\operatorname{SplitInfo} _{B}(Z)}=\frac{0.997-0.778}{1.371}=0.160 \\ \\g_{r}(Z, C)=\frac{g(Z \mid C)}{\operatorname{SplitInfo} _{C}(Z)}=\frac{\operatorname{Info}(Z)-\operatorname{Info} (Z \mid C)}{\operatorname{SplitInfo} _{C}(Z)}=\frac{0.997-0.459}{0.971}=0.554 \\ \\g_{r}(Z, E)=\frac{g(Z \mid E)}{\operatorname{SplitInfo} _{E}(Z)}=\frac{\operatorname{Info}(Z)-\operatorname{Info} (Z \mid D)}{\operatorname{SplitInfo} _{D}(Z)}=\frac{0.997-0.393}{2.156}=0.280 \end{array}$