【车间调度】基于matlab混合蛙跳算法 (SFLA) 求解简单调度问题【含Matlab源码 2247期】

⛄一、车间调度简介

在传统的SFLA中，每一个青蛙的位置代表一个解，若干个青蛙组成的种群代表一个解的集合，种群被划分为不同的组，即模因组，对每个模因组执行搜索过程，当达到终止条件后，重新将模因组合并成新的种群，这个过程称作种群重组。搜索和重组过程持续进行直到满足终止条件。

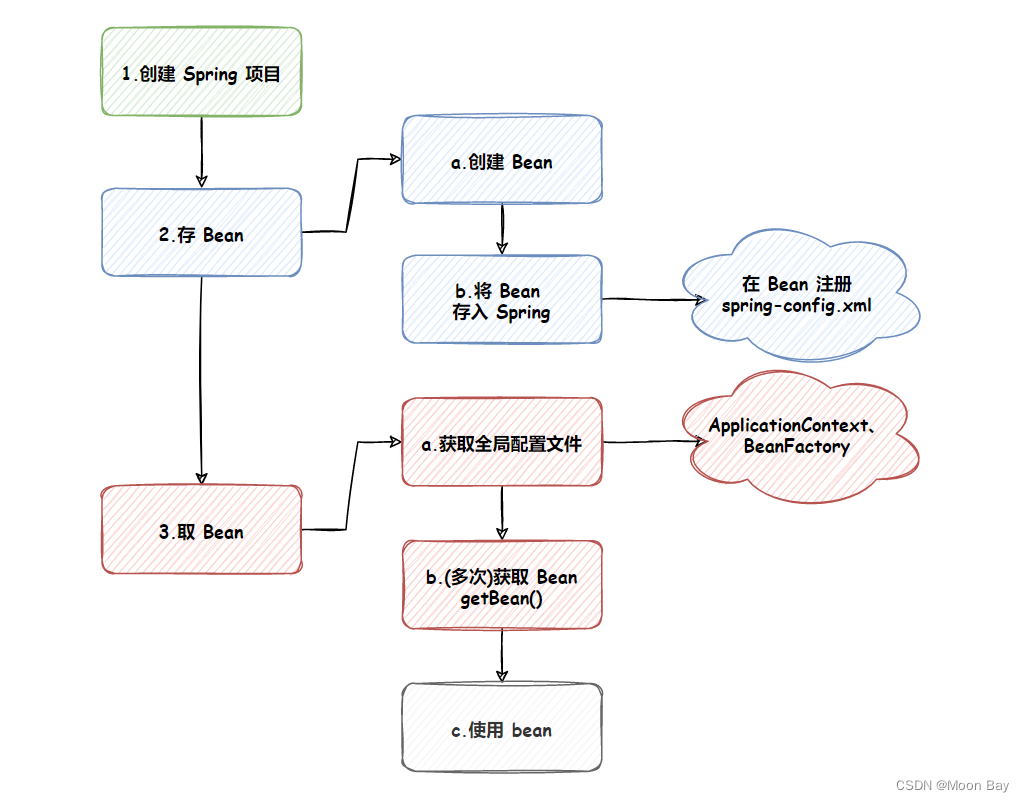
在FJSP中，每一个青蛙代表一个个体，即一个可行解，每一个可行解都有一个评价其优劣的指标，即目标值。考虑到传统SFLA依靠位置更新公式来产生新解，这种方式难以应用于FJSP这种离散问题中，所以需要对SFLA离散化，构建合理的编码解码以及搜索重组方式。
　
1 编码
FJSP包含两个基本问题，即工序调度问题和机器分配问题,因此，该问题的解决方案通常由两部分组成[16,17,18],工序串和机器串，工序串表示所有工件的加工顺序，机器串表示工件对应所选择的加工机器号。一个3×3的FJSP实例如表1所示。其中“2”表示第一个工件的第一道工序在1号机器上加工的时间为2,“-”表示该工件的该道工序不能在该机器上加工，以此类推。一个完整的解决方案可以表示为{[132123]|[332112]},第一部分{[1 3 2 1 2 3]}表示工序加工顺序，数字代表工件号，数字出现的次数则代表对应工件的第几道工序。第二部分{[3 3 2 1 1 2]}表示对应工件所选择的加工机器。　
表1 3×3FJSP实例
在这里插入图片描述
2 解码
解码是为了将工序串和机器串转换所求的目标值，在此基础上合理地安排各个工件在机器上加工，从而使得目标值最优。本文为了实现染色体解码对解空间的高效搜索，设计了一种进化贪婪插入法(evolutionary greedy insertion, EGI),其解码过程如图1所示。
在这里插入图片描述
图1 EGI解码过程示意图
工序Oij即将在机器Mb上加工，根据当前加工情况，有三段空闲可供选择，Idle1、Idle2和Idle3三段空闲时间均大于等于Oij的加工时间。Idle1的开始时间小于Oi(j-1)结束时间，故不满足约束条件。Idle2和Idle3都满足约束条件，而Idle2更接近Oij的加工时间，所以选择Idle2插入。相对于一般的解码方法，EGI提供了更多可供选择的空闲时间段，更利于找到最优解。

3 种群初始化
初始种群质量的优劣对于算法而言至关重要，一个高质量的种群能够为算法的进化提供一个优越的起点，使算法减少从差解到优解的搜寻时间。本算法采用了ZHANG等[19]提出的GLS初始化方法，即全局选择(global selection, GS)、局部选择(local selection, LS)和随机选择(random selection, RS),除此以外，再加入一种全局最小化(global minimization, GM)方法，选择可选机器集中加工时间最短的那一台机器进行加工。在上述多种启发式规则启发下生成的初始种群能够为算法的进化提供一个较好的起点，加快算法的整体收敛速度。

4 族群划分
混合蛙跳算法区别于其他算法最大的特点就是对种群进行分组，而传统的随机划分方式由于不能平衡各个组内青蛙的优劣程度，会大大增加算法求解的随机性，使得算法的收敛速度变慢。本文算法采用LEI等[20]提出的二元锦标赛选择方式将种群划分成w个族群V(V1,V2,…,Vw),先从种群中选择最好的w个个体依次作为每个族群中的第一个个体，再从余下的个体中利用锦标赛选择法补充每个族群的剩余个体，即从剩下的种群中随机选择两个个体Q1和Q2,优秀的那一个个体进入V1,作为V1中的第二个个体，较差的那个返回种群；再从种群中随机选择两个个体，较好的那一个进入V2,作为V2中的第二个个体，以此类推，直至所有的族群被填满。

5 族群内进化策略
对于每一个族群内的个体来说，如果都采用相同的进化策略，则难以对不同质量的个体进行有针对性的进化，所以为了避免盲目进化，通常在各自族群内部会区分出优劣个体，然后对其采用不同的更新策略进行优化。对族群中优秀的个体采用邻域搜索，加强对更优解的挖掘。对族群中的劣势解，则采用全局加局部结合的协调优化策略，平衡整个族群中个体的优劣程度，加快算法的收敛速度。

6 更新策略
6.1 交叉操作
交叉的目的是为了获得新的个体，在尽量保证优良基因不被破坏的情况下，对解空间进行高效搜索，因而交叉操作应该满足可行性、继承性和非冗余性。针对FJSP的特性，ZHANG等[21]提出的POX交叉法，因其具有低约束性，并且可以避免冲突检测，所以被普遍用来完成对工序编码层的交叉操作。本文对POX交叉法进行局部改进，提出一种改进的交叉法(improved intersection method, IIM),具体步骤如下：

步骤1:选出两条染色体P1、P2作为父代，P1=[1 3 2 4 3 1 2 4 3],P2=[3 1 1 2 4 4 2 3 3];

步骤2:将工件集J={1,2,3,4}分为两个非空子集，J1={1,2},J2={3,4};

步骤3:复制P1中包含在J1中的基因按原顺序插入子代染色体C1中，复制P2中包含在J1中的基因按原顺序插入子代染色体C2中；

步骤4:复制P2中包含在J2中的基因按原顺序插入C1中，复制P1中包含在J2中的基因按原顺序插入C2中，得到C1=[1 3 2 4 4 1 2 3 3],C2=[3 1 1 2 4 3 2 4 3];

步骤5:对C1、C2进行倒序操作得到C3、C4,C3=[3 3 2 1 4 4 2 3 1],C4=[3 4 2 3 4 2 1 1 3],对C1、C2、C3、C4进行解码操作，选取最优的两个解代替C1、C2。

而对于机器编码层采用多点交叉方式，可避免产生非法解。具体步骤如下：

步骤1:随机选择两条机器染色体L1和L2,L1=[1 2 5 3 4 2 6 1 5],L2=[3 3 5 2 1 4 2 3 3];

步骤2:生成一个和机器染色体维度一样的0、1数组X,X=[0 0 1 1 0 0 1 0 0];

步骤3:找到矩阵中所有1所在的位置；

步骤4:将所有位置1上的L1和L2的基因对换得到L1′和L2′,L1′=[1 2 5 2 4 2 2 1 5],L2′=[3 3 4 3 4 2 6 3 3]。

6.2 局部搜索操作
为了提高算法的搜索能力和开发能力，在保持种群多样性的同时又能够提高算法的收敛能力，本文算法采用了分别针对于工序编码层和机器编码层的局部搜索策略。

(1)针对工序编码层OS,采用如下步骤进行局部搜索操作：
步骤1:选择一条工序染色体P,P=[1 3 2 4 1 1 2 2 3];

步骤2:随机选择两个工序数相等的工件J1和J2,J1={1},J2={2},找出它们所有工序在染色体中的位置；

步骤3:交换两个工件对应所有工序的位置，并保持原来的顺序，得到新的工染色体P′,P′=[2 3 1 4 2 2 1 1 3]。

(2)针对机器编码层，结合图2具体搜索步骤如下：
步骤1:选择一组染色体，其中工序染色体为P,P=[1 1 2 3 3 1 4 2 4];机器染色体为L,L=[2 1 3 2 3 1 3 2 1];对应加工时间矩阵为T,T=[1 2 1 3 1 4 1 2 2 ];

步骤2:计算出所有机器上的总负载Ptotal,Ptotal=[8 6 3];最大完成时间Cmax,Cmax=9;计算得到所有机器的负载率，其中每台机器的负载率P=Ptotal/Cmax,P=[0.89 0.67 0.33],并排序得到负载率最高和最低的机器；

步骤3:在满足约束条件的情况下，从负载率最高的机器上选择该机器加工的最后一道工序移动到负载率最低的那一台机器上，从图2可以看出，在未进行该局部搜索时，最大完成时间为9,经过该局部搜索，将M1上的O42移动到M3上，得到的最大完成时间为8。
在这里插入图片描述
图2 机器局部搜索

7 ISFLA算法整体框架
根据上述改进策略，结合FJSP,提出的ISFLA框架流程图如图3所示。
在这里插入图片描述
图3 ISFLA流程图

⛄二、部分源代码

function pop = RunFLA(pop, params)

%% FLA Parameters
q = params.q; % Number of Parents
alpha = params.alpha; % Number of Offsprings
beta = params.beta; % Maximum Number of Iterations
sigma = params.sigma;
CostFunction = params.CostFunction;
VarMin = params.VarMin;
VarMax = params.VarMax;
VarSize = size(pop(1).Position);
BestSol = params.BestSol;

nPop = numel(pop); % Population Size
P = 2*(nPop+1-(1:nPop))/(nPop*(nPop+1)); % Selection Probabilities

% Calculate Population Range (Smallest Hypercube)
LowerBound = pop(1).Position;
UpperBound = pop(1).Position;
for i = 2:nPop
LowerBound = min(LowerBound, pop(i).Position);
UpperBound = max(UpperBound, pop(i).Position);
end

%% FLA Main Loop

for it = 1:beta

% Select Parents
L = RandSample(P, q);
B = pop(L);

% Generate Offsprings
for k = 1:alpha

% Sort Population
[B, SortOrder] = SortPopulation(B);
L = L(SortOrder);

% Flags
ImprovementStep2 = false;
Censorship = false;

% Improvement Step 1
NewSol1 = B(end);
Step = sigmarand(VarSize).(B(1).Position-B(end).Position);
NewSol1.Position = B(end).Position + Step;
if IsInRange(NewSol1.Position, VarMin, VarMax)
[NewSol1.Cost NewSol1.Sol] = CostFunction(NewSol1.Position);
if NewSol1.Cost<B(end).Cost
B(end) = NewSol1;
else
ImprovementStep2 = true;
end
else
ImprovementStep2 = true;
end

% Improvement Step 2
if ImprovementStep2
NewSol2 = B(end);
Step = sigmarand(VarSize).(BestSol.Position-B(end).Position);
NewSol2.Position = B(end).Position + Step;
if IsInRange(NewSol2.Position, VarMin, VarMax)
[NewSol2.Cost NewSol2.Sol] = CostFunction(NewSol2.Position);
if NewSol2.Cost<B(end).Cost
B(end) = NewSol2;
else
Censorship = true;
end
else
Censorship = true;
end
end