【数论】试除法判断质数，分解质因数，筛质数

news2024/12/23 6:31:32

Halo，这里是Ppeua。平时主要更新C语言，C++，数据结构算法......感兴趣就关注我吧！你定不会失望。

🌈个人主页：主页链接

🌈算法专栏：专栏链接

现已更新完KMP算法、排序模板，之后我会继续往里填充内容哒。

🌈LeetCode专栏：专栏链接

目前在刷初级算法的LeetBook 。若每日一题当中有力所能及的题目，也会当天做完发出

🌈代码仓库：Gitee链接

🌈点击关注=收获更多优质内容🌈

用一篇Blog来讲解下最近学到的数论，为日后的刷题打下坚实的基础。

试除法判断质数：

朴素做法：

代码模板:

改进做法：

代码模板:

分解质因数：

代码模板:

筛质数：

埃式筛法:

欧拉筛(线性筛):

完结撒花：

什么是质数？

一个大于1的自然数，除了1和它自身外，不能被其他自然数整除的数

试除法判断质数：

朴素做法：

将定义进行模拟，若整除了除1与其自身的另外的数，则为质数

代码模板:

#include<iostream>
using namespace std;
int n;
void prime(int x)
{
    if(x<2){
        cout<<"No"<<endl;
        return;}
    for(int i=2;i<=x;i++)
    {
        if(x%i==0)
        {
            cout<<"No"<<endl;
            return ;
        }
    }
    cout<<"Yes"<<endl;
    return;
}
int main()
{
    cin>>n;
    while(n--)
    {
        int x;
        cin>>x;
        prime(x);
    }
}

改进做法：

一个数的两个因数都是成对出现的，例如：6的因数为 1 2 3 6

这里的2与3是成对出现的。所以我们无需从2-x的范围去遍历，因为若前半部分没有出现，则后半部分必然没有其因数

通过反证法：若后半部分有其因数，则就会出现这两个因数相乘会大于其本身。

所以应该满足 i*i<=x的范围,但又因为i*i在数字极大的情况下,很容易溢出,所以改成i<=x/i

代码模板:

#include<iostream>
using namespace std;
int n;
void prime(int x)
{
    if(x<2){
        cout<<"No"<<endl;
        return;}
    for(int i=2;i<=x/i;i++)
    {
        if(x%i==0)
        {
            cout<<"No"<<endl;
            return ;
        }
    }
    cout<<"Yes"<<endl;
    return;
}
int main()
{
    cin>>n;
    while(n--)
    {
        int x;
        cin>>x;
        prime(x);
    }
}

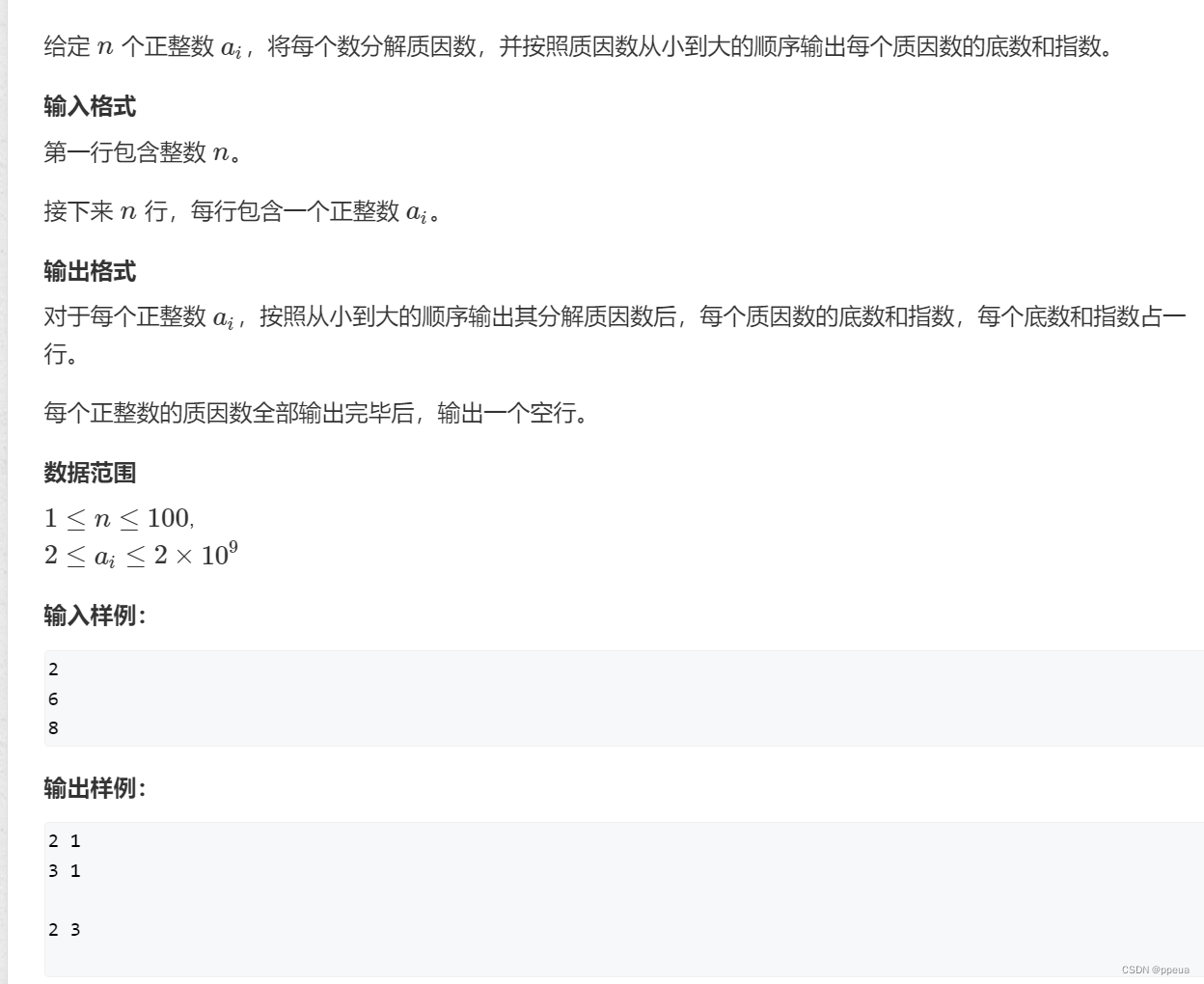
分解质因数：

与上文相同,依然是用到了i*i<=n的这个性质,需要注意一下,最多存在一个>=sqrt(n)的质因子,同样可以用反证法来证明,这里就不过多赘述.所以当最后跳出循环时若还存在x>1,也就是没有被模掉的情况时,则认为x为其较大的那个因子,也需要放进去.

若一个数能整除i,则i是其一个因子,又因为我们从小到达进行遍历,被整除的这个i必然为质因子,因为若为普通因子,在循环整除的时候已经被消掉了,化为其指数.

代码模板:

#include<iostream>
using namespace std;
void divide(int x)
{

    for(int i=2;i<=x/i;i++)
        if(x%i==0)
        {
            int s=0;
            while(x%i==0)
            {
                x/=i;
                s++;
            }
            printf("%d %d\n",i,s);
        }
        if(x>1)printf("%d %d\n",x,1);
        puts("");
        return ;
}
int main()
{
    int n=0;
    cin>>n;
    while(n--)
    {
        int x;
        cin>>x;
        divide(x);
    }
    return 0;
}

筛质数：

埃式筛法:

一个约数其必然可以由数相乘得到.

假设有如下2到10的数

埃式筛法的核心就是:从头遍历每个数字,将其与每一个小于本身它本身的质数相乘,再将之后的数标记为非质数

也就是这样

可以看出这里的质数就为2 3 5 7,

但我们很快就会发现,这个算法有一个弊端,假设这里的范围到12,就会出现当4*3的时候把十二标记为false了,但6*2又会将其标记一次,十分的不优雅.

所以就提出了另一个改进的算法

欧拉筛(线性筛):

当发现相乘的这个质数为其最小质因子时,则停止遍历

#include<iostream>
using namespace std;
const int N=1e6+9;
bool st[N];
int prime[N];
int main()
{
    int n=0;
    int cnt=0;
    cin>>n;
    for(int i=2;i<=n;i++)
    {
        if(!st[i])
        {
            prime[cnt++]=i;
        }
        for(int j=0;prime[j]<=n/i;j++)
        {
            st[prime[j]*i]=true;
            if(i%prime[j]==0)break;
        }
        
    }
    cout<<cnt;
}