目录
1. 计算阶乘的和 ★
2. 基本计算器 ★★★
3. N皇后 II ★★★
🌟 每日一练刷题专栏
C/C++ 每日一练 专栏
Python 每日一练 专栏
1. 计算阶乘的和
计算:1!-2!+3!-4!+5!-6!+7!-8!+9!-10!,并输出计算结果。
注意:不全是加法,而是 ∑ n! * (-1)^(n-1),加减混合的“代数和”。
代码:
#include "stdio.h"
double fun(int n)
{
double sum=1.0;
int i;
for(i=1;i<=n;i++)
sum*=i;
return sum;
}
int main()
{
int i,mark=1;
double sum=0,item=0;
for(i=1;i<=10;i++)
{
item=mark*fun(i);
sum+=item;
mark=-mark;
}
printf("1!-2!+3!-4!+5!-6!+7!-8!+9!-10! = %.0lf\n",sum);
return 0;
}输出:
1!-2!+3!-4!+5!-6!+7!-8!+9!-10! = -3301819
也可以不用像上面原题附带的代码一样自定义阶乘函数,其实只用一个循环就能搞定,非常简洁:
#include "stdio.h"
int main()
{
long sum=0, fac=-1;
for(int i=1;i<=10;i++)
{
fac *= -i;
sum += fac;
}
printf("1!-2!+3!-4!+5!-6!+7!-8!+9!-10! = %ld\n", sum);
return 0;
}
2. 基本计算器
给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。
示例 1:
输入:s = "1 + 1" 输出:2
示例 2:
输入:s = " 2-1 + 2 " 输出:3
示例 3:
输入:s = "(1+(4+5+2)-3)+(6+8)" 输出:23
提示:
1 <= s.length <= 3 * 10^5s由数字、'+'、'-'、'('、')'、和' '组成s表示一个有效的表达式
代码:
#include <bits/stdc++.h>
using namespace std;
class Solution
{
public:
int calculate(string s)
{
stack<int> myStack;
stack<char> myOperator;
int i;
for (i = 0; i < s.length(); i++)
{
while (i < s.length() && s[i] == ' ')
i++;
if (i == s.length())
break;
if (s[i] == '+' || s[i] == '-' || s[i] == '(')
myOperator.push(s[i]);
else if (s[i] == ')')
{
while (myOperator.top() != '(')
{
int element1 = myStack.top();
myStack.pop();
int element2 = myStack.top();
myStack.pop();
char op = myOperator.top();
myOperator.pop();
if (op == '+')
myStack.push(element1 + element2);
else if (op == '-')
myStack.push(element2 - element1);
}
if (!myOperator.empty())
myOperator.pop();
while (!myOperator.empty() && (myOperator.top() != '('))
{
int element1 = myStack.top();
myStack.pop();
int element2 = myStack.top();
myStack.pop();
char op = myOperator.top();
myOperator.pop();
if (op == '+')
myStack.push(element1 + element2);
else if (op == '-')
myStack.push(element2 - element1);
}
}
else
{
long long int number = 0;
int j = i;
while (j < s.length() && (s[j] - '0' <= 9) && (s[j] - '0' >= 0))
{
number = number * 10 + (s[j] - '0');
j++;
}
i = j - 1;
myStack.push(number);
while (!myOperator.empty() && (myOperator.top() != '('))
{
int element1 = myStack.top();
myStack.pop();
int element2 = myStack.top();
myStack.pop();
char op = myOperator.top();
myOperator.pop();
if (op == '+')
myStack.push(element1 + element2);
else if (op == '-')
myStack.push(element2 - element1);
}
}
}
return myStack.top();
}
};
int main()
{
Solution sol;
string s = "1 + 1";
cout << sol.calculate(s) << endl;
s = "2-1 + 2";
cout << sol.calculate(s) << endl;
s = "(1+(4+5+2)-3)+(6+8)";
cout << sol.calculate(s) << endl;
return 0;
}输出:
2
3
23
3. N皇后 II
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回 n 皇后问题 不同的解决方案的数量。
示例 1:
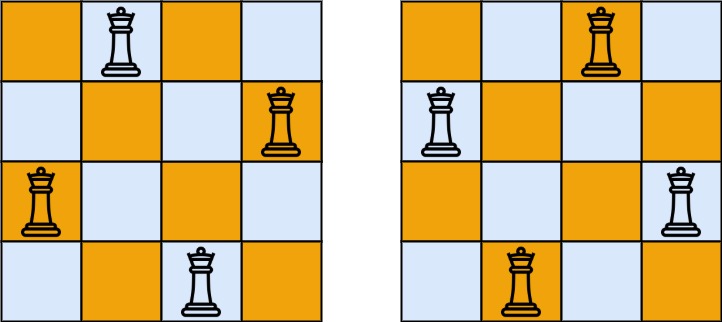
输入:n = 4 输出:2 解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1 输出:1
提示:
1 <= n <= 9- 皇后彼此不能相互攻击,也就是说:任何两个皇后都不能处于同一条横行、纵行或斜线上。
代码:
#include <bits/stdc++.h>
using namespace std;
class Solution
{
public:
int totalNQueens(int n)
{
vector<int> stack(n);
return dfs(n, 0, stack);
}
private:
int dfs(int n, int row, vector<int> &stack)
{
int count = 0;
if (row == n)
{
return count + 1;
}
else
{
for (int i = 0; i < n; i++)
{
if (row == 0 || !conflict(stack, row, i))
{
stack[row] = i;
count += dfs(n, row + 1, stack);
}
}
return count;
}
}
bool conflict(vector<int> &stack, int row, int col)
{
for (int i = 0; i < row; i++)
{
if (col == stack[i] || abs(row - i) == abs(col - stack[i]))
{
return true;
}
}
return false;
}
};
int main()
{
Solution sol;
cout << sol.totalNQueens(4) << endl;
cout << sol.totalNQueens(1) << endl;
return 0;
}输出:
2
1
附录
贪心算法
又称贪婪算法, greedy algorithm
是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,算法得到的是在某种意义上的局部最优解。贪心算法不是对所有问题都能得到整体最优解,关键是贪心策略的选择。
一般步骤
①建立数学模型来描述问题 。
②把求解的问题分成若干个子问题 。
③对每个子问题求解,得到子问题的局部最优解 。
④把子问题的解局部最优解合成原来解问题的一个解 。
贪心算法是一种对某些求最优解问题的更简单、更迅速的设计技术。贪心算法的特点是一步一步地进行,常以当前情况为基础根据某个优化测度作最优选择,而不考虑各种可能的整体情况,省去了为找最优解要穷尽所有可能而必须耗费的大量时间。贪心算法采用自顶向下,以迭代的方法做出相继的贪心选择,每做一次贪心选择,就将所求问题简化为一个规模更小的子问题,通过每一步贪心选择,可得到问题的一个最优解。虽然每一步上都要保证能获得局部最优解,但由此产生的全局解有时不一定是最优的,所以贪心算法不要回溯 。
使用条件
利用贪心法求解的问题应具备如下2个特征:
1、贪心选择性质
一个问题的整体最优解可通过一系列局部的最优解的选择达到,并且每次的选择可以依赖以前作出的选择,但不依赖于后面要作出的选择。这就是贪心选择性质。对于一个具体问题,要确定它是否具有贪心选择性质,必须证明每一步所作的贪心选择最终导致问题的整体最优解。
2、最优子结构性质
当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质。问题的最优子结构性质是该问题可用贪心法求解的关键所在。在实际应用中,至于什么问题具有什么样的贪心选择性质是不确定的,需要具体问题具体分析。
存在问题
贪心算法也存在如下问题:
1、不能保证解是最佳的。因为贪心算法总是从局部出发,并没从整体考虑 ;
2、贪心算法一般用来解决求最大或最小解 ;
3、贪心算法只能确定某些问题的可行性范围 。
应用实例
例如,平时购物找零钱时,为使找回的零钱的硬币数最少,不要求找零钱的所有方案,而是从最大面值的币种开始,按递减的顺序考虑各面额,先尽量用大面值的面额,当不足大面值时才去考虑下一个较小面值,这就是贪心算法。
有很多经典的应用,比如霍夫曼编码,普利姆和克鲁斯卡尔最小生成树算法,还有迪杰斯特拉单源最短路径算法,都是使用了这种思维。
(附录部分摘自百度百科)
🌟 每日一练刷题专栏
✨ 持续,努力奋斗做强刷题搬运工!
👍 点赞,你的认可是我坚持的动力!
★ 收藏,你的青睐是我努力的方向!
✏️ 评论,你的意见是我进步的财富!
 | C/C++ 每日一练 专栏 |
 | Python 每日一练 专栏 |