引言

我们知道Transformer很好用，但它设定的最长长度是512。像一篇文章超过512个token是很容易的，那么我们在处理这种长文本的情况下也想利用Transformer的强大表达能力需要怎么做呢？

本文就带来一种处理长文本的Transformer变种——Transformer-XL，它也是XLNet的基石。这里的XL取自EXTRAL LONG。

论文题目：Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context

论文地址：https://arxiv.org/pdf/1901.02860.pdf

Transformer

我们先来简单回顾下Transformer，不熟悉的可以先看关于Transformer论文全文翻译——[论文翻译]Attention Is All You Need
。

我们重点回顾输入向量的计算方式，如上图底部所示，词嵌入(Embedding) ➕ 位置编码(Positional Encoding)。

假设有两个输入token，它们的位置分别在$i,j$处，用$x_i,x_j$相应地表示。
记
$E_{x_i}^T\in {\mathbb{R}}^{1\times d}$为token $x_i$的词嵌入，$E_{x_j}$为 token $x_j$的词嵌入；
$U_i^T\in {\mathbb{R}}^{1\times d}$和$U_j^T\in {\mathbb{R}}^{1\times d}$分别为第$i$和第$j$处的位置编码。

这里$d$为嵌入大小。

一般向量默认是列向量，而行向量表示需要加上个转置。所以，上面两个记号上有转置。

那么在计算token $x_j$相对于token $x_j$的Self-Attention时，首先会计算出$q_i$和$k_j$：
$$\begin{gathered} q_i=(E_{x_i}^T+U_i^T)W_q^T\in {\mathbb{R}}^{1\times d} \\ {k}_j=(E_{x_j}+U_j)W_k^T\in {\mathbb{R}}^{1\times d}\text{\hspace{1em}(1)} \end{gathered}$$
其中$W_q^T$和$W_k^T\in {\mathbb{R}}^{d\times d}$。

这里把词嵌入＋位置编码分开写，后面会看到为什么这么做。

接下来，在计算它们两之间的注意力得分时，直接拿这两个向量做点积得到一个标量，注意维度：
$$\begin{array}{rl}{q}_i\cdot k_j^T& =(E_{x_i}^T+U_i^T)W_q^T\cdot {\left((E_{x_j}^T+U_j^T)W_k^T\right)}^T\\ & =(E_{x_i}^T{W}_q^T+U_i^T{W}_q^T)\cdot (W_k{E}_{x_j}+W_k{U}_j)\\ & =E_{x_i}^T{W}_q^T{W}_k{E}_{x_j}+E_{x_i}^T{W}_q^T{W}_k{U}_j+U_i^T{W}_q^T{W}_k{E}_{x_j}+U_i^T{W}_q^T{W}_k{U}_j\end{array}\text{\hspace{1em}(2)}$$

相当于把它们进行了展开，整个过程应该没什么问题。

下面进入本文的主题。

Transformer-XL

我们先来看如果想在Transformer中处理长文本的话，要怎么做呢？

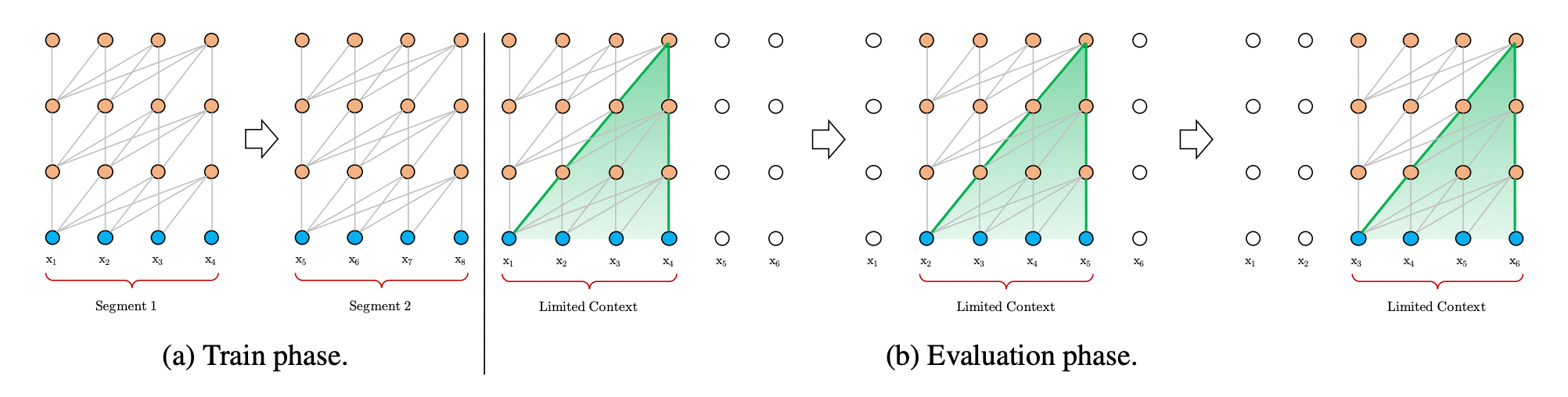
图1: Transformer中处理长文本的传统方法

比如传统的做法就是将长文本切分成固定长度的块(segment)，并为每个块单独编码，块与块之间没有信息流动(正向传播与反向传播)。这样会导致两个问题，一是模型无法捕获长期依赖(long-term dependency)；另一个是在分块之后，后面块在进行预测时没有前面块的信息，使模型存在优化难和表现差的问题，这被称为上下文碎片问题(context fragmentation problem)。

而Transformer-XL的提出就是为了处理(address)上面的两个问题。

上图给出了块长度为4时的一个示例，可以看到，在训练阶段，Transformer分别对第一个块中的序列$x_1,x_2,x_3,x_4$和第二块中的序列$x_5,x_6,x_7,x_8$进行建模(modeling)。
而在评估(evaluation)阶段，为了不将文本切成块，会通过类似移动窗口的方式，一个一个token地向后移动，这种方法效率非常低下。

为此，Transformer-XL提出了两种改进策略——块级别循环(Segment-level Recurrent)和相对位置编码(Relative Positional Encoding)。

我们先来看第一个。

块级别循环

块级别循环，全称是状态复用的块级别循环(Segment-Level Recurrence with State Reuse)。如下图(a)部分：

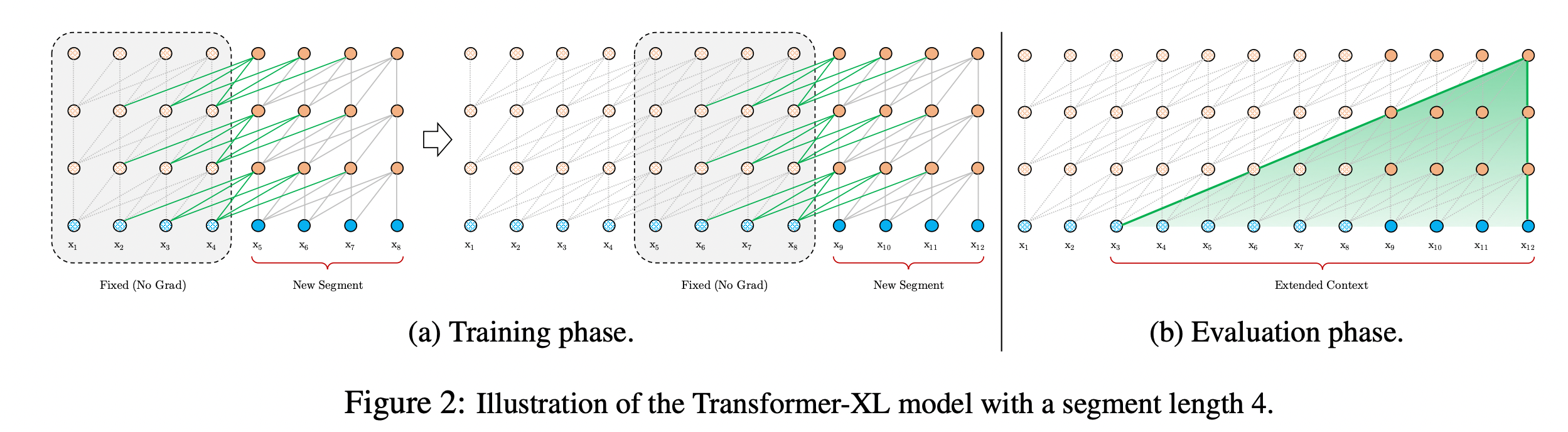
图2: Transformer-XL中处理长文本的方法

上面有两个块，每个块都会做Self-Attention，块之间有一些绿色的连线。在第二个块的时候，可以把第一个块的某些信息通过绿色的连线传递过来，那么它是怎么实现的呢？

实际上非常简单，它的思想是，在跑完第一个块的信息后，把它中间所有的隐藏层向量都缓存起来，然后跑第二个块的信息时，可以拿到这些缓存向量。

下面用公式描述一下，假设两个连续长度为$L$的块分别为$s_{\tau }=x_{\tau ,1},\cdots ,x_{\tau ,L}$和$s_{\tau +1}=x_{\tau +1,1},\cdots ,x_{\tau +1,L}$。记由第$\tau$个块$s_{\tau }$在第$n$层上产生的隐藏状态序列$h_{\tau }^n\in {\mathbb{R}}^{L\times d}$，$d$为隐藏层维度大小。
那么对于片段$s_{\tau +1}$在第$n$层上的隐藏状态$h_{\tau +1}^n$计算如下：
$${\tilde{h}}_{\tau +1}^{n-1}=[\text{SG}(h_{\tau }^{n-1})\circ h_{\tau +1}^{n-1}]\text{\hspace{1em}(3)}$$
$$q_{\tau +1}^n,k_{\tau +1}^n,v_{\tau +1}^n=h_{\tau +1}^{n-1}{W}_q^T,{\tilde{h}}_{\tau +1}^{n-1}{W}_k^T,{\tilde{h}}_{\tau +1}^{n-1}{W}_v^T\text{\hspace{1em}(4)}$$
$$h_{\tau +1}^n=\text{Transformer-Layer}(q_{\tau +1}^n,k_{\tau +1}^n,v_{\tau +1}^n)\text{\hspace{1em}(5)}$$

其中函数$\text{SG}(\cdot )$表示停止梯度传输；记号$[h_u\circ h_v]$表示沿着长度(时间步)维度拼接两个隐藏状态序列；$W$表示全连接权重。
这里通过拼接当前块第$n-1$层的隐藏状态和缓存的前一块第$n-1$层的隐藏状态来生成扩展的上下文${\tilde{h}}_{\tau +1}^{n-1}$。

与传统的Transformer的主要不同点在于键$k_{\tau +1}^n$和值$v_{\tau +1}^n$的计算依赖于扩展的上下文${\tilde{h}}_{\tau +1}^{n-1}$，即用到了前一块的缓存信息$h_{\tau }^{n-1}$。
同时可以看到在计算查询$q_{\tau +1}^n$时只会基于当前块来计算。这种设计体现在了上图(a)的绿线中。

这种状态复用的块级别循环机制应用于语料库中每两个连续的块，本质上是在隐藏状态下产生一个块级别的循环。在这种机制下，Transformer利用的有效上下文可以远远超出两个块。注意到这种在$h_{\tau +1}^n$和$h_{\tau }^{n-1}$的循环依赖每块间向下移动一层，与传统RNN中的同层循环不同。因此，最大可能的依赖长度随块的长度$L$和层数$N$呈线性增长。这种机制和RNN中常用的随时间反向传播机制(Back Propagation Through Time,BPTT)类似。然而，在这里是将整个序列的隐藏层状态全部缓存，而不是像BPTT机制中只会保留最后一个状态。

在训练的时候，先训练第一块，更新完第一块的权重后，然后固定中间的隐藏状态向量。在训练第二块的时候，读取刚才保存那些向量，在训练第二块的时候，还是只更新第二块的权重，不过可以隐式地用到第一块的信息(通过绿线传递过来)。梯度不会沿着绿线进行更新，因此实际上学的还是一个块之间的信息。

通过这种方式可以延长依赖的长度到N倍，N就是网络的深度(块的个数)。

这样解决了上下文碎片问题，让模型可以捕获到长期依赖的信息。而评估阶段就更简单了，此时可以直接拿到全部的上下文信息，沿着上面的绿线将信息向后传递，而不需要像图1(b)那样从头开始计算。每次可以以块进行移动，而不是以token为单位进行移动，大大加快了推理过程。

虽然它的思想很简单，但如果直接实现的话会发现表现很差，因为这里还有一个问题，就是不连贯的位置编码问题。这就涉及到了第二个改进策略，相对位置编码。

相对位置编码

如果直接简单地把原来Transformer的绝对位置编码信息应用到块级别的循环上就会很奇怪：
$$[0,1,2,3]\to [0,1,2,3,0,1,2,3]$$

假设和上面的例子一样，块长度限制为4。现在长度为8之后就会变成两个单独的块，对应的位置编码就成了$[0,1,2,3,0,1,2,3]$。

这样模型无法区分第一个块的第2个位置编码和第二个块的第2个位置编码，认为是一样的，这显然是不合理的。因为位置编码的目的是为了引入位置信息。Transformer-XL针对这种情况提出了相对位置编码。

位置信息的重要性体现在注意力分数的计算上面，在传统Transformer中，同一块(segment)内的查询$q_i$和键向量$k_j$的注意力分数计算如下：

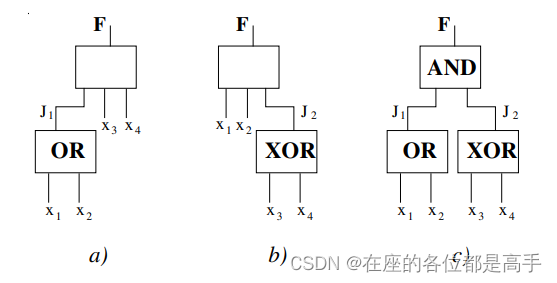
就是上文公式$(2)$，拆分成四项后，为每项进行编号，从$(a)$到$(d)$。

$E_{x_i}^T\in {\mathbb{R}}^{1\times d}$为token $x_i$的词嵌入，$E_{x_j}$为 token $x_j$的词嵌入；
$U_i^T\in {\mathbb{R}}^{1\times d}$和$U_j^T\in {\mathbb{R}}^{1\times d}$分别为第$i$和第$j$处的绝对位置编码。

原本的做法里面，位置嵌入是绝对位置，因此如果是第i个位置，这个$U_i$都会是一样的(不管是哪个块)。

基于仅依赖相对位置信息的思想，Transformer-XL提出了改进如下：

其中为每项进行编号，从下面展开描述一下它的改进点：

• 将$(b)$和$(d)$项中计算key向量的绝对位置嵌入$U_j$替换为相对位置$R_{i-j}$，代表一个相对距离信息。注意这里的$R$是传统Transformer中的正弦函数编码模式，是不需要学习的。
• 引入一个可学习的参数$u$$\in {\mathbb{R}}^d$去替换$(c)$项中的query向量$U_i^T{W}_q^T$。这样新的query向量$u$对于所有的位置都是一样的，因为是以位置$i$为基准点，所以$i$使用的位置嵌入是一个固定的嵌入，只需要考虑$i$和$j$之间相关位置的关系。同理，用可学习的参数$v$$\in {\mathbb{R}}^d$去替换$(d)$项中的$U_i^T{W}_q^T$。
• 将$W_k$分成两个权重矩阵$W_{k,E}$和$W_{k,R}$，以分别产生基于内容的key向量和基于位置的key向量。

在新的计算公式中，每项都有直观的意义：

• $(a)$项表示基于内容的相关度，计算query $x_i$和key $x_j$内容之间的关联信息；
• $(b)$项捕获内容相关的位置偏置，计算query $x_i$的内容与key $x_j$的位置编码之间的关联信息，$R_{i-j}$表示两者的相对位置信息，取$R$中的第$i-j$行；
• $(c)$项表示全局内容偏置，计算query $x_i$的位置编码与key $x_j$的内容之间的关联信息；
• $(d)$项表示全局位置偏置，计算query $x_i$与key $x_j$的位置编码之间的关联信息；

把块级别循环和相对位置编码的信息合并后，我们就得到了Transformer-XL的最终架构。对于一个$N$层的Transformer-XL的单个注意力头，对于$n=1,\cdots ,N$有：

这样对于每个query，所有的位置嵌入都是一样的，对于不同的token注意力偏差也是一样的。

这里的注意力偏差怎么理解？原始的Transformer中的位置编码，对于每个位置都会学一个向量，假设某个token经常出现在第一个位置，比如“今年”这个token，那么模型学到的位置编码可能会包含“今年”这个token的意思，而没有其他不常出现在第一个位置的token信息。也就说第一个位置编码对“今年”产生了偏差。