1. 合并两个有序数组

给你两个有序整数数组 nums1 和 nums2，请你将 nums2 合并到 nums1 中，使 nums1 成为一个有序数组。

初始化 nums1 和 nums2 的元素数量分别为 m 和 n 。你可以假设 nums1 的空间大小等于 m + n，这样它就有足够的空间保存来自 nums2 的元素。

示例 1：

输入：nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出：[1,2,2,3,5,6]

示例 2：

输入：nums1 = [1], m = 1, nums2 = [], n = 0
输出：[1]

提示：

nums1.length == m + n
nums2.length == n
0 <= m, n <= 200
1 <= m + n <= 200
-10^9 <= nums1[i], nums2[i] <= 10^9

代码：

class Solution(object):
    def merge(self, nums1, m, nums2, n):
        """
        :type nums1: List[int]
        :type m: int
        :type nums2: List[int]
        :type n: int
        :rtype: void Do not return anything, modify nums1 in-place instead.
        """
        p1, p2 = m - 1, n - 1
        pos = m + n - 1
        while p1 >= 0 and p2 >= 0:
            if nums1[p1] >= nums2[p2]:
                nums1[pos] = nums1[p1]
                p1 -= 1
            else:
                nums1[pos] = nums2[p2]
                p2 -= 1
            pos -= 1
        while p2 >= 0:
            nums1[pos] = nums2[p2]
            p2 -= 1
            pos -= 1
        return nums1
    
# %%
s = Solution()
print(s.merge(nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3))

输出：

[1, 2, 2, 3, 5, 6]

2. 二叉树的右视图

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例 1:

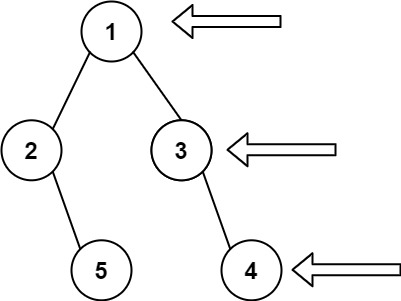
输入: [1,2,3,null,5,null,4]
输出: [1,3,4]

示例 2:

输入: [1,null,3]
输出: [1,3]

示例 3:

输入: []
输出: []

提示:

二叉树的节点个数的范围是 [0,100]
-100 <= Node.val <= 100

代码：

class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

class Solution:
    def rightSideView(self, root: TreeNode) -> list:
        if not root:
            return []
        res = []
        curnode = [root]
        nexnode = []
        res.append(curnode[0].val)
        while curnode:
            for s in curnode:
                if s.right:
                    nexnode.append(s.right)
                if s.left:
                    nexnode.append(s.left)
            if nexnode:
                res.append(nexnode[0].val)
            curnode = nexnode
            nexnode = []
        return res

def listToTree(lst: list) -> TreeNode:
    if not lst:
        return None
    root = TreeNode(lst[0])
    queue = [root]
    i = 1
    while i < len(lst):
        node = queue.pop(0)
        if lst[i] is not None:
            node.left = TreeNode(lst[i])
            queue.append(node.left)
        i += 1
        if i < len(lst) and lst[i] is not None:
            node.right = TreeNode(lst[i])
            queue.append(node.right)
        i += 1
    return root

def inorderTraversal(root: TreeNode) -> list:
    if not root:
        return []
    res = []
    res += inorderTraversal(root.left)
    res.append(root.val)
    res += inorderTraversal(root.right)
    return res

# %%
s = Solution()
null = None

nums = [1,2,3,null,5,null,4]
root = listToTree(nums)
print(s.rightSideView(root))
print(inorderTraversal(root))  #test

nums = [1,null,3]
root = listToTree(nums)
print(s.rightSideView(root))
print(inorderTraversal(root))  #test

输出：

[1, 3, 4]
[2, 5, 1, 3, 4]
[1, 3]
[1, 3]

3. 拼接最大数

给定长度分别为 m 和 n 的两个数组，其元素由 0-9 构成，表示两个自然数各位上的数字。现在从这两个数组中选出 k (k <= m + n) 个数字拼接成一个新的数，要求从同一个数组中取出的数字保持其在原数组中的相对顺序。

求满足该条件的最大数。结果返回一个表示该最大数的长度为 k 的数组。

说明: 请尽可能地优化你算法的时间和空间复杂度。

示例 1:

输入:
nums1 = [3, 4, 6, 5]
nums2 = [9, 1, 2, 5, 8, 3]
k = 5
输出:[9, 8, 6, 5, 3]

示例 2:

输入:
nums1 = [6, 7]
nums2 = [6, 0, 4]
k = 5
输出:[6, 7, 6, 0, 4]

示例 3:

输入:
nums1 = [3, 9]
nums2 = [8, 9]
k = 3
输出:[9, 8, 9]

代码：

class Solution:
    def maxNumber(self, nums1: list, nums2: list, k: int) -> list:
        def pick_max(nums, k):
            stack = []
            drop = len(nums) - k
            for num in nums:
                while drop and stack and stack[-1] < num:
                    stack.pop()
                    drop -= 1
                stack.append(num)
            return stack[:k]
        def merge(A, B):
            lst = []
            while A or B:
                bigger = A if A > B else B
                lst.append(bigger[0])
                bigger.pop(0)
            return lst
        return max(
            merge(pick_max(nums1, i), pick_max(nums2, k - i))
            for i in range(k + 1)
            if i <= len(nums1) and k - i <= len(nums2)
        )
# %%
s = Solution()
print(s.maxNumber(nums1 = [3,4,6,5], nums2 = [9,1,2,5,8,3], k = 5))
print(s.maxNumber(nums1 = [6,7], nums2 = [6,0,4], k = 5))
print(s.maxNumber(nums1 = [3,9], nums2 = [8,9], k = 3))

输出：

[9, 8, 6, 5, 3]
[6, 7, 6, 0, 4]
[9, 8, 9]

注：max(迭代推导式) --> max(i for i in [3,6,4,5] if i%2)