先遣兵
在了解 disjoint support decomposition 之前,先学习两个基本的概念。
- disjoint
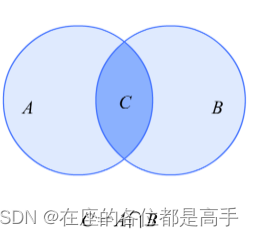
数学含义上的两个集合交集,所谓非相交,即交集为空集。
A
∩
B
=
C
=
⊘
A \cap B = C = \oslash
A∩B=C=⊘
- support
逻辑综合中的 s u p p o r t support support 概念是指: 一个门 g g g 的 s u p p o r t support support 是指该门 g g g 的所有原始输入 P I PI PI。
例如有一个函数:
F
o
u
t
=
h
(
x
)
+
g
(
x
)
Fout = h(x) + g(x)
Fout=h(x)+g(x)
其中
h
(
x
)
=
A
+
B
h(x) = A + B
h(x)=A+B,
g
(
x
)
=
D
+
E
g(x) = D + E
g(x)=D+E,则
n
o
d
e
node
node
h
h
h 和
g
g
g 的
s
u
p
p
o
r
t
support
support 分别为 { A, B }、{ D, E },
F
o
u
t
Fout
Fout 的
s
u
p
p
o
r
t
support
support 为 { A, B, D, E }。
其他概念有兴趣可参考 逻辑综合知识点总结 持续更新中…
1. 简介
disjoint support decomposition ,它是用于优化布尔函数的一种技术,将其分解成具有不交 s u p p o r t support support 的较小子函数。
一个布尔函数可以表示为 (sum of products,SOP)表达式或积和式(product of sums,POS)表达式。
disjoint support decomposition 的目的是将给定表达式转换为具有较小且更易于处理的子表达式的形式。它的基本思想是识别原始表达式中没有共同变量的变量子集,并将表达式分解为只取决于这些子集的较小表达式的和。这使得函数更容易进行优化,因为较小的表达式通常更容易处理。
即:
非相交分解 == 一个函数
F
F
F可以被子函数
K
K
K 和
J
J
J 表示,且
K
K
K 和
J
J
J 的
s
u
p
p
o
r
t
support
support 不相交,且 4J$ 只有一个输出,
F
=
K
(
x
1
,
x
2
,
.
.
.
,
x
j
−
1
,
J
(
x
j
,
.
.
.
,
x
n
)
)
F = K (x_1, x_2, ..., x_{j-1}, J(x_j, ..., x_n))
F=K(x1,x2,...,xj−1,J(xj,...,xn))
例如有一个函数:
F
=
(
x
1
+
x
2
)
(
x
3
⊕
x
4
)
F = (x_1 + x_2)(x_3 \oplus x_4)
F=(x1+x2)(x3⊕x4)
最简单的
d
s
d
dsd
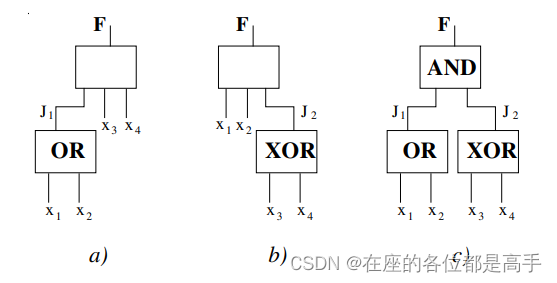
dsd 为图 (a) 所示:
K
=
(
x
3
⊕
x
4
)
J
1
,
J
1
=
(
x
1
+
x
2
)
K = (x_3 \oplus x_4)J_1, J_1 = (x_1 + x_2)
K=(x3⊕x4)J1,J1=(x1+x2)
或者图 (b):
K
=
(
x
1
+
x
2
)
J
2
,
J
2
=
(
x
3
⊕
x
4
)
K = (x_1 + x_2)J_2, J_2 = (x_3 \oplus x_4)
K=(x1+x2)J2,J2=(x3⊕x4)
再进一步表示为图 ©
F
=
K
(
J
1
,
J
2
)
=
(
x
1
+
x
2
)
(
x
3
⊕
x
4
)
F = K(J_1, J_2) = (x_1 + x_2)(x_3 \oplus x_4)
F=K(J1,J2)=(x1+x2)(x3⊕x4)
如果一个
o
u
t
p
u
t
output
output 被全部用
d
s
d
dsd
dsd 表示,这意味着拿掉某一个
s
u
p
p
o
r
t
support
support 不会对其他的
s
u
p
p
o
r
t
support
support 支持的逻辑造成影响,个人理解是否可以通过
d
s
d
dsd
dsd 分解由局部最优达到全局最优。
如果
F
F
F被一个
D
A
G
(
G
)
DAG(G)
DAG(G) 表示的话,也可以表示为,应该比较容易理解:
E
d
g
e
(
G
)
=
E
d
g
e
(
K
)
+
E
d
g
e
(
J
)
Edge(G) = Edge(K) + Edge(J)
Edge(G)=Edge(K)+Edge(J)
2. 算法
TODO
3. 优点
TODO