python实现波士顿房价预测---(2)

news2025/1/14 1:14:55

计算梯度

继续上一篇的内容python实现波士顿房价预测—(1)。
梯度计算公式中引入计算因子 1 2 \frac{1}{2} 21​，为了计算更加简洁。
L = 1 2 N ∑ i = 1 N ( y i − z i ) 2 L=\frac{1}{2N}\sum_{i=1}^{N}(y_i - z_i)^2 L=2N1​∑i=1N​(yi​−zi​)2

其中 z i z_i zi​是模型对于第i个样本的预测值:

z i = ∑ j = 0 12 x i j . w j + b z_i = \sum_{j=0}^{12}x_{i}^{j}.w_j + b zi​=∑j=012​xij​.wj​+b

梯度的定义：
g r a d i e n t = ( ∂ L ∂ w 0 , ∂ L ∂ w 1 ， ∂ L ∂ w 2 ， ∂ L ∂ w 3 ， . . . ∂ L ∂ b ) gradient =(\frac{\partial L}{\partial w_0},\frac{\partial L}{\partial w_1}，\frac{\partial L}{\partial w_2}，\frac{\partial L}{\partial w_3}，...\frac{\partial L}{\partial b}) gradient=(∂w0​∂L​,∂w1​∂L​，∂w2​∂L​，∂w3​∂L​，...∂b∂L​)

所以基于上面的损失函数计算梯度的表达式，分别计算w和b的偏导数：

∂ L ∂ w j = 1 N ∑ i = 1 N ( z i − y i ) ∂ z i ∂ w j = 1 N ∑ i = 1 N ( z i − y i ) x i j \frac{\partial L}{\partial w_j}=\frac{1}{N}\sum_{i=1}^{N}(z_i-y_i)\frac{\partial z_i}{\partial w_j}=\frac{1}{N}\sum_{i=1}^{N}(z_i-y_i)x_{i}^{j} ∂wj​∂L​=N1​∑i=1N​(zi​−yi​)∂wj​∂zi​​=N1​∑i=1N​(zi​−yi​)xij​

b:

∂ L ∂ b = 1 N ∑ i = 1 N ( z i − y i ) ∂ z i ∂ b = 1 N ∑ i = 1 N ( z i − y i ) \frac{\partial L}{\partial b}=\frac{1}{N}\sum_{i=1}^{N}(z_i-y_i)\frac{\partial z_i}{\partial b}=\frac{1}{N}\sum_{i=1}^{N}(z_i-y_i) ∂b∂L​=N1​∑i=1N​(zi​−yi​)∂b∂zi​​=N1​∑i=1N​(zi​−yi​)

前面为什么要加一个 1 2 \frac{1}{2} 21​，是因为在求导的时候会产生一个2，整好抵消。
下面我们考虑只有一个样本情况来计算梯度：

L = 1 2 ( z i − y i ) 2 L=\frac{1}{2}(z_i-y_i)^2 L=21​(zi​−yi​)2
第一个样本数据:
z 1 = x 1 0 . w 0 + x 1 1 . w 1 + x 1 2 . w 2 + x 1 3 . w 3 + x 1 4 . w 4 + x 1 5 . w 5 + x 1 6 . w 6 + x 1 7 . w 7 + . . . + x 1 12 . w 12 + b z_1=x_{1}^{0}.w_0+x_{1}^{1}.w_1+x_{1}^{2}.w_2+x_{1}^{3}.w_3+x_{1}^{4}.w_4+x_{1}^{5}.w_5+x_{1}^{6}.w_6+x_{1}^{7}.w_7+...+x_{1}^{12}.w_{12}+b z1​=x10​.w0​+x11​.w1​+x12​.w2​+x13​.w3​+x14​.w4​+x15​.w5​+x16​.w6​+x17​.w7​+...+x112​.w12​+b

带入 L L L表达式中:
L = 1 2 ( x 1 0 . w 0 + x 1 1 . w 1 + x 1 2 . w 2 + b − y 1 ) 2 L=\frac{1}{2}(x_{1}^{0}.w_0+x_{1}^{1}.w_1+x_{1}^{2}.w_2+b -y_1)^2 L=21​(x10​.w0​+x11​.w1​+x12​.w2​+b−y1​)2

开始计算w和b的偏导数:
∂ L ∂ w 0 = ( x 1 0 . w 0 + x 1 1 . w 1 + x 1 2 . w 2 + b − y 1 ) . x 1 0 = ( z i − y i ) . x 1 0 \frac{\partial L}{\partial w_0}=(x_{1}^{0}.w_0+x_{1}^{1}.w_1+x_{1}^{2}.w_2+b -y_1).x_{1}^{0}=(z_i-y_i).x_{1}^{0} ∂w0​∂L​=(x10​.w0​+x11​.w1​+x12​.w2​+b−y1​).x10​=(zi​−yi​).x10​
…
∂ L ∂ b = ( x 1 0 . w 0 + x 1 1 . w 1 + x 1 2 . w 2 + b − y 1 ) = ( z i − y i ) \frac{\partial L}{\partial b}=(x_{1}^{0}.w_0+x_{1}^{1}.w_1+x_{1}^{2}.w_2+b -y_1)=(z_i-y_i) ∂b∂L​=(x10​.w0​+x11​.w1​+x12​.w2​+b−y1​)=(zi​−yi​)

接下来通过代码查查数据。

x1 = x[0]
y1 = y[0]
z1 = net.forward(x1)
print('x1 {}, shape {}'.format(x1, x1.shape))
print('y1 {}, shape {}'.format(y1, y1.shape))
print('z1 {}, shape {}'.format(z1, z1.shape))

x1 [0. 0.18 0.07344184 0. 0.31481481 0.57750527
0.64160659 0.26920314 0. 0.22755741 0.28723404 1.
0.08967991], shape (13,)
y1 [0.42222222], shape (1,)
z1 [130.86954441], shape (1,)
按照上面推到的公式：

w0
gradient_w0 = (z1 - y1) * x1[0]
print('gradient_w0 {}'.format(gradient_w0))
w1
gradient_w1 = (z1 - y1) * x1[1]
print('gradient_w1 {}'.format(gradient_w1))

那么在Numpy里面的广播机制（向量和矩阵都是可以看做一个单一变量），可以快速实现梯度计算。计算梯度 ( z 1 − y 1 ) . x 1 (z_1-y_1).x_1 (z1​−y1​).x1​得到一个13维度的向量，表示在第一个样本在第一层神经网络中每一个神经元的影像。

gradient_w = (z1 - y1) * x1
print('gradient_w_by_sample1 {}, gradient.shape {}'.format(gradient_w, gradient_w.shape))

输入数据中有多个样本，每个样本都对梯度有贡献。如上代码计算了只有样本1时的梯度值，同样的计算方法也可以计算样本2和样本3对梯度的贡献。

x2 = x[1]
y2 = y[1]
z2 = net.forward(x2)
gradient_w = (z2 - y2) * x2
print('gradient_w_by_sample2 {}, gradient.shape {}'.format(gradient_w, gradient_w.shape))

可能有的读者再次想到可以使用for循环把每个样本对梯度的贡献都计算出来，然后再作平均。但是我们不需要这么做，仍然可以使用Numpy的矩阵操作来简化运算，如3个样本的情况。

# 注意这里是一次取出3个样本的数据，不是取出第3个样本
x3samples = x[0:3]
y3samples = y[0:3]
z3samples = net.forward(x3samples)

print('x {}, shape {}'.format(x3samples, x3samples.shape))
print('y {}, shape {}'.format(y3samples, y3samples.shape))
print('z {}, shape {}'.format(z3samples, z3samples.shape))

x [[0.00000000e+00 1.80000000e-01 7.34418420e-02 0.00000000e+00
  3.14814815e-01 5.77505269e-01 6.41606591e-01 2.69203139e-01
  0.00000000e+00 2.27557411e-01 2.87234043e-01 1.00000000e+00
  8.96799117e-02]
 [2.35922539e-04 0.00000000e+00 2.62405717e-01 0.00000000e+00
  1.72839506e-01 5.47997701e-01 7.82698249e-01 3.48961980e-01
  4.34782609e-02 1.14822547e-01 5.53191489e-01 1.00000000e+00
  2.04470199e-01]
 [2.35697744e-04 0.00000000e+00 2.62405717e-01 0.00000000e+00
  1.72839506e-01 6.94385898e-01 5.99382080e-01 3.48961980e-01
  4.34782609e-02 1.14822547e-01 5.53191489e-01 9.87519166e-01
  6.34657837e-02]], shape (3, 13)
y [[0.42222222]
 [0.36888889]
 [0.66      ]], shape (3, 1)
z [[130.86954441]
 [108.34434338]
 [131.3204395 ]], shape (3, 1)

上面的x3samples, y3samples, z3samples的第一维大小均为3，表示有3个样本。下面计算这3个样本对梯度的贡献。

gradient_w = (z3samples - y3samples) * x3samples
print('gradient_w {}, gradient.shape {}'.format(gradient_w, gradient_w.shape))

gradient_w [[0.00000000e+00 2.34805180e+01 9.58029163e+00 0.00000000e+00
  4.10667496e+01 7.53340159e+01 8.36958617e+01 3.51168286e+01
  0.00000000e+00 2.96842549e+01 3.74689117e+01 1.30447322e+02
  1.16985043e+01]
 [2.54738434e-02 0.00000000e+00 2.83333765e+01 0.00000000e+00
  1.86624242e+01 5.91703008e+01 8.45121992e+01 3.76793284e+01
  4.69458498e+00 1.23980167e+01 5.97311025e+01 1.07975454e+02
  2.20777626e+01]
 [3.07963708e-02 0.00000000e+00 3.42860463e+01 0.00000000e+00
  2.25832858e+01 9.07287666e+01 7.83155260e+01 4.55955257e+01
  5.68088867e+00 1.50027645e+01 7.22802431e+01 1.29029688e+02
  8.29246719e+00]], gradient.shape (3, 13)

上面 g r a d i e n t w gradient_w gradientw​的维度是(3,13)。第一行的数据与前面x1计算的梯度是一样的，第二行与x2的梯度一致。所以我们看到Numpy的广播机制带来的便捷：

  • 一方面可以扩展参数的维度w0到w12。
  • 也可以扩展样本的维度，从第一个样本到405个样本对于参数的梯度计算。
z = net.forward(x)
gradient_w = (z - y) * x
print('gradient_w shape {}'.format(gradient_w.shape))
print(gradient_w)

gradient_w shape (404, 13)
[[0.00000000e+00 2.34805180e+01 9.58029163e+00 ... 3.74689117e+01
  1.30447322e+02 1.16985043e+01]
 [2.54738434e-02 0.00000000e+00 2.83333765e+01 ... 5.97311025e+01
  1.07975454e+02 2.20777626e+01]
 [3.07963708e-02 0.00000000e+00 3.42860463e+01 ... 7.22802431e+01
  1.29029688e+02 8.29246719e+00]
 ...
 [3.97706874e+01 0.00000000e+00 1.74130673e+02 ... 2.01043762e+02
  2.48659390e+02 1.27554582e+02]
 [2.69696515e+01 0.00000000e+00 1.75225687e+02 ... 2.02308019e+02
  2.34270491e+02 1.28287658e+02]
 [6.08972123e+01 0.00000000e+00 1.53017134e+02 ... 1.76666981e+02
  2.18509161e+02 1.08772220e+02]]

我们可以看到在numpy的广播机制下，计算损失函数对于w的偏导数结果(403,13)维度，每一行表示一个样本对于总梯度的贡献，根据计算公式，总梯度w等于每个样本的梯度的平均值：
∂ L ∂ w j = 1 N ∑ i = 1 N ( z i − y i ) ∂ z i ∂ w j = 1 N ∑ i = 1 N ( z i − y i ) x i j \frac{\partial L}{\partial w_j}=\frac{1}{N}\sum_{i=1}^{N}(z_i-y_i)\frac{\partial z_i}{\partial w_j}=\frac{1}{N}\sum_{i=1}^{N}(z_i-y_i)x_{i}^{j} ∂wj​∂L​=N1​∑i=1N​(zi​−yi​)∂wj​∂zi​​=N1​∑i=1N​(zi​−yi​)xij​

使用numpy的均值函数:

# axis = 0 表示把每一行做相加然后再除以总的行数
gradient_w = np.mean(gradient_w, axis=0)
print('gradient_w ', gradient_w.shape)
print('w ', net.w.shape)
print(gradient_w)
print(net.w)

gradient_w  (13,)
w  (13, 1)
[  4.6555403   19.35268996  55.88081118  14.00266972  47.98588869
  76.87210821  94.8555119   36.07579608  45.44575958  59.65733292
  83.65114918 134.80387478  38.93998153]
[[ 1.76405235e+00]
 [ 4.00157208e-01]
 [ 9.78737984e-01]
 [ 2.24089320e+00]
 [ 1.86755799e+00]
 [ 1.59000000e+02]
 [ 9.50088418e-01]
 [-1.51357208e-01]
 [-1.03218852e-01]
 [ 1.59000000e+02]
 [ 1.44043571e-01]
 [ 1.45427351e+00]
 [ 7.61037725e-01]]

更新函数里面梯度下降的函数

class Network(object):
    def __init__(self, num_of_weights):
        # 随机产生w的初始值
        # 为了保持程序每次运行结果的一致性，此处设置固定的随机数种子
        np.random.seed(0)
        self.w = np.random.randn(num_of_weights, 1)
        self.b = 0.
        
    def forward(self, x):
        z = np.dot(x, self.w) + self.b
        return z
    
    def loss(self, z, y):
        error = z - y
        num_samples = error.shape[0]
        cost = error * error
        cost = np.sum(cost) / num_samples
        return cost
    
    def gradient(self, x, y):
        z = self.forward(x)
        gradient_w = (z-y)*x
        gradient_w = np.mean(gradient_w, axis=0)
        gradient_w = gradient_w[:, np.newaxis]
        gradient_b = (z - y)
        gradient_b = np.mean(gradient_b)
        
        return gradient_w, gradient_b

查看一下w5,w9对应的loss值

# 调用上面定义的gradient函数，计算梯度
# 初始化网络
net = Network(13)
# 设置[w5, w9] = [-100., -100.]
net.w[5] = -100.0
net.w[9] = -100.0

z = net.forward(x)
loss = net.loss(z, y)
gradient_w, gradient_b = net.gradient(x, y)
gradient_w5 = gradient_w[5][0]
gradient_w9 = gradient_w[9][0]
print('point {}, loss {}'.format([net.w[5][0], net.w[9][0]], loss))
print('gradient {}'.format([gradient_w5, gradient_w9]))

确定梯度更新

首先沿着梯度的反方向移动一小步，找到下一个点P1，观察损失函数的变化。

# 在[w5, w9]平面上，沿着梯度的反方向移动到下一个点P1
# 定义移动步长 eta
eta = 0.1
# 更新参数w5和w9
net.w[5] = net.w[5] - eta * gradient_w5
net.w[9] = net.w[9] - eta * gradient_w9
# 重新计算z和loss
z = net.forward(x)
loss = net.loss(z, y)
gradient_w, gradient_b = net.gradient(x, y)
gradient_w5 = gradient_w[5][0]
gradient_w9 = gradient_w[9][0]
print('point {}, loss {}'.format([net.w[5][0], net.w[9][0]], loss))
print('gradient {}'.format([gradient_w5, gradient_w9]))

point [-95.41203171187678, -96.4497631155171], loss 7214.694816482369
gradient [-43.883932999069096, -34.019273908495926]

上面语句中梯度的更新：
net.w[5] = net.w[5] - eta * gradient_w5
其中有两个点：

  • 相减：参数需要向梯度的反方向移动。
  • eta: 控制每次参数值沿着梯度反方向变动的大小，即每次移动的步长，又称为学习率。

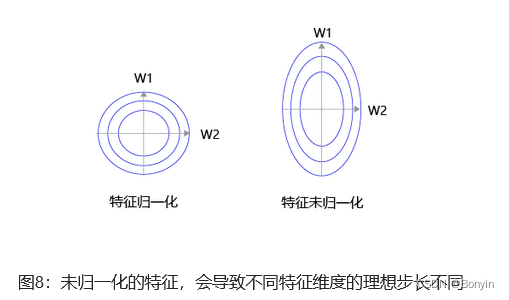
这里大家可以思考一下？为什么在数据处理阶段需要做归一化操作，保持尺度一致？这是为了统一步长更加合适。
图8，特征输入归一化后，不同参数输出的Loss是一个比较规整的曲线，学习率可以设置成统一的值 ；特征输入未归一化时，不同特征对应的参数所需的步长不一致，尺度较大的参数需要大步长，尺寸较小的参数需要小步长，导致无法设置统一的学习率。
在这里插入图片描述自定义类更新，训练函数train。

class Network(object):
    def __init__(self, num_of_weights):
        # 随机产生w的初始值
        # 为了保持程序每次运行结果的一致性，此处设置固定的随机数种子
        np.random.seed(0)
        self.w = np.random.randn(num_of_weights,1)
        self.w[5] = -100.
        self.w[9] = -100.
        self.b = 0.
        
    def forward(self, x):
        z = np.dot(x, self.w) + self.b
        return z
    
    def loss(self, z, y):
        error = z - y
        num_samples = error.shape[0]
        cost = error * error
        cost = np.sum(cost) / num_samples
        return cost
    
    def gradient(self, x, y):
        z = self.forward(x)
        gradient_w = (z-y)*x
        gradient_w = np.mean(gradient_w, axis=0)
        gradient_w = gradient_w[:, np.newaxis]
        gradient_b = (z - y)
        gradient_b = np.mean(gradient_b)        
        return gradient_w, gradient_b
    
    def update(self, gradient_w5, gradient_w9, eta=0.01):
        net.w[5] = net.w[5] - eta * gradient_w5
        net.w[9] = net.w[9] - eta * gradient_w9
        
    def train(self, x, y, iterations=100, eta=0.01):
        points = []
        losses = []
        for i in range(iterations):
            points.append([net.w[5][0], net.w[9][0]])
            z = self.forward(x)
            L = self.loss(z, y)
            gradient_w, gradient_b = self.gradient(x, y)
            gradient_w5 = gradient_w[5][0]
            gradient_w9 = gradient_w[9][0]
            self.update(gradient_w5, gradient_w9, eta)
            losses.append(L)
            if i % 50 == 0:
                print('iter {}, point {}, loss {}'.format(i, [net.w[5][0], net.w[9][0]], L))
        return points, losses

# 获取数据
train_data, test_data = load_data()
x = train_data[:, :-1]
y = train_data[:, -1:]
# 创建网络
net = Network(13)
num_iterations=2000
# 启动训练
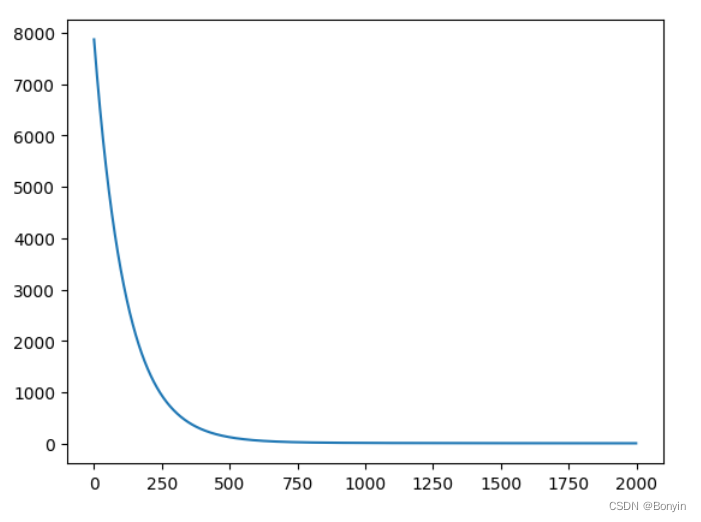
points, losses = net.train(x, y, iterations=num_iterations, eta=0.01)

# 画出损失函数的变化趋势
plot_x = np.arange(num_iterations)
plot_y = np.array(losses)
plt.plot(plot_x, plot_y)
plt.show()

在这里插入图片描述

扩展训练到全部参数

上面演示只是包含了w5和w9两个参数。但是房价预测的完整模型，必须要对所有参数w和b求解。修改类中的update和train函数。

class Network(object):
    def __init__(self, num_of_weights):
        # 随机产生w的初始值
        # 为了保持程序每次运行结果的一致性，此处设置固定的随机数种子
        np.random.seed(0)
        self.w = np.random.randn(num_of_weights, 1)
        self.b = 0.
        
    def forward(self, x):
        z = np.dot(x, self.w) + self.b
        return z
    
    def loss(self, z, y):
        error = z - y
        num_samples = error.shape[0]
        cost = error * error
        cost = np.sum(cost) / num_samples
        return cost
    
    def gradient(self, x, y):
        z = self.forward(x)
        gradient_w = (z-y)*x
        gradient_w = np.mean(gradient_w, axis=0)
        gradient_w = gradient_w[:, np.newaxis]
        gradient_b = (z - y)
        gradient_b = np.mean(gradient_b)        
        return gradient_w, gradient_b
    
    def update(self, gradient_w, gradient_b, eta = 0.01):
        self.w = self.w - eta * gradient_w
        self.b = self.b - eta * gradient_b
        
    def train(self, x, y, iterations=100, eta=0.01):
        losses = []
        for i in range(iterations):
            z = self.forward(x)
            L = self.loss(z, y)
            gradient_w, gradient_b = self.gradient(x, y)
            self.update(gradient_w, gradient_b, eta)
            losses.append(L)
            if (i+1) % 10 == 0:
                print('iter {}, loss {}'.format(i, L))
        return losses
# 获取数据
train_data, test_data = load_data()
x = train_data[:, :-1]
y = train_data[:, -1:]
# 创建网络
net = Network(13)
num_iterations=1000
# 启动训练
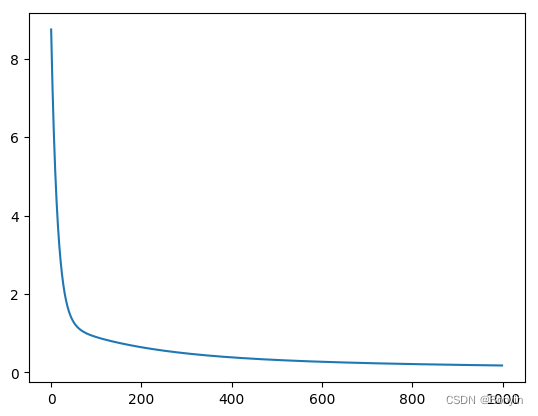
losses = net.train(x,y, iterations=num_iterations, eta=0.01)

# 画出损失函数的变化趋势
plot_x = np.arange(num_iterations)
plot_y = np.array(losses)
plt.plot(plot_x, plot_y)
plt.show()

在这里插入图片描述

随机梯度下降

在上述梯度计算过程中，每次都是基于全部数据，对于波士顿房价预测数据集，样本少。但是在实际问题中，数据集都是非常大，每次使用全量数据效率非常低。一个合理的解决方案是每次从总的数据集中随机抽取出小部分数据来代表整体，基于这部分数据计算梯度和损失来更新参数，这种方法被称作随机梯度下降法（SGD）。核心概念：

  • min-batch:每次迭代时抽取出来的一批数据被称为一个minibatch。
  • batch_size: 每个minibatch所包含的样本数目称为batch size。
  • epcoh: 当程序迭代的时候，按minibatch逐渐抽取出样本，当把整个数据集都遍历到了的时候，则完成了一轮训练，也叫一个Epoch（轮次）
import numpy as np

class Network(object):
    def __init__(self, num_of_weights):
        # 随机产生w的初始值
        # 为了保持程序每次运行结果的一致性，此处设置固定的随机数种子
        #np.random.seed(0)
        self.w = np.random.randn(num_of_weights, 1)
        self.b = 0.
        
    def forward(self, x):
        z = np.dot(x, self.w) + self.b
        return z
    
    def loss(self, z, y):
        error = z - y
        num_samples = error.shape[0]
        cost = error * error
        cost = np.sum(cost) / num_samples
        return cost
    
    def gradient(self, x, y):
        z = self.forward(x)
        N = x.shape[0]
        gradient_w = 1. / N * np.sum((z-y) * x, axis=0)
        gradient_w = gradient_w[:, np.newaxis]
        gradient_b = 1. / N * np.sum(z-y)
        return gradient_w, gradient_b
    
    def update(self, gradient_w, gradient_b, eta = 0.01):
        self.w = self.w - eta * gradient_w
        self.b = self.b - eta * gradient_b
            
                
    def train(self, training_data, num_epochs, batch_size=10, eta=0.01):
        n = len(training_data)
        losses = []
        for epoch_id in range(num_epochs):
            # 在每轮迭代开始之前，将训练数据的顺序随机打乱
            # 然后再按每次取batch_size条数据的方式取出
            np.random.shuffle(training_data)
            # 将训练数据进行拆分，每个mini_batch包含batch_size条的数据
            mini_batches = [training_data[k:k+batch_size] for k in range(0, n, batch_size)]
            for iter_id, mini_batch in enumerate(mini_batches):
                #print(self.w.shape)
                #print(self.b)
                x = mini_batch[:, :-1]
                y = mini_batch[:, -1:]
                a = self.forward(x)
                loss = self.loss(a, y)
                gradient_w, gradient_b = self.gradient(x, y)
                self.update(gradient_w, gradient_b, eta)
                losses.append(loss)
                print('Epoch {:3d} / iter {:3d}, loss = {:.4f}'.
                                 format(epoch_id, iter_id, loss))
        
        return losses

# 获取数据
train_data, test_data = load_data()

# 创建网络
net = Network(13)
# 启动训练
losses = net.train(train_data, num_epochs=50, batch_size=100, eta=0.1)

# 画出损失函数的变化趋势
plot_x = np.arange(len(losses))
plot_y = np.array(losses)
plt.plot(plot_x, plot_y)
plt.show()

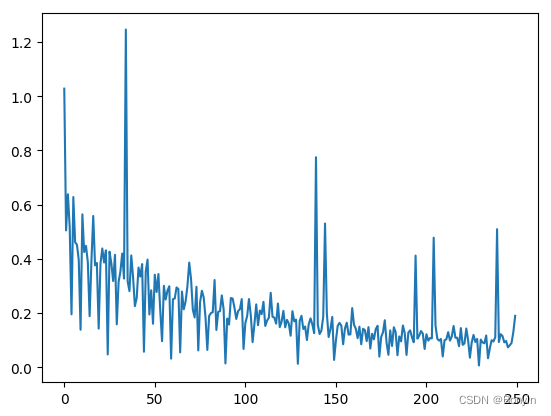在这里插入图片描述观察上述损失函数的变化，随机梯度下降加快了训练过程，但由于每次仅基于少量样本更新参数和计算损失ii，所以损失下降曲线会出现震荡。
————————————————————————
说明
由于房价预测的数据集样本太少，感受不到随机梯度下将带来的性能提升。
————————————————————————

总结

在使用numpy构建神经网络三点要素：

  • 构建网络，初始化参数 w w w和 b b b，定义预测和损失函数的计算方法。
  • 随机选择初始点，建立梯度的计算方法和参数更新方式
  • 将数据集的数据按batch size的大小分成多个minibatch，分别灌入模型计算梯度并更新参数，不断迭代直到损失函数几乎不再下降。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/402553.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【halcon】轮廓拟合相关函数

【halcon】轮廓拟合相关函数

涉及函数 edges_sub_pix 寻找边缘 edges_sub_pix (Image, Edges, canny, 1, 10, 20) 后面三个参数，越小，找到的细节越多。这个是对应录波器为canny时。 canny滤波器用的最多。 segment_contours_xld 将连续的轮廓进行分段，按圆弧或者执…
阅读更多...
软件测试13

软件测试13

Linux命令 1.pwd：查看当前所在的路径位置 2.ls：查看当前路径下有哪些文件 3.cd：切换路径 4.touch：创建普通文件，可以创建单文件，也可以创建多文件（touch a，touch b c） 5…
阅读更多...
【专项训练】高级搜索

【专项训练】高级搜索

高级搜索，这部分非常烧脑，可略过！ 包括：剪枝、双向BFS、启发式搜索！ 启发式搜索：优先队列，即优先级搜索！ 回溯：分治 + 试错 数独问题，类似八皇后！ 36. 有效的数独 https://leetcode.cn/problems/valid-sudoku/description/ class Solution(object
阅读更多...
Java【二叉搜索树和哈希表】模拟实现 + 【Map和Set】介绍

Java【二叉搜索树和哈希表】模拟实现 + 【Map和Set】介绍

文章目录前言一、二叉搜索树1、什么是二叉搜索树2、模拟实现二叉搜索树2.1, 查找2.2, 插入2.3, 删除3、性能分析二、模型三、哈希表1、什么是哈希表1.1, 什么是哈希冲突1.2, 避免, 解决哈希冲突1.2.1, 避免: 调节负载因子1.2.2, 解决1: 闭散列(了解)1.2.3, 解决2: 开散列/哈希桶…
阅读更多...
基于卷积神经网络CNN的水果分类预测，卷积神经网络水果等级识别

基于卷积神经网络CNN的水果分类预测，卷积神经网络水果等级识别

目录 背影 卷积神经网络CNN的原理 卷积神经网络CNN的定义 卷积神经网络CNN的神经元 卷积神经网络CNN的激活函数 卷积神经网络CNN的传递函数 卷积神经网络CNN水果分类预测 基本结构 主要参数 MATALB代码 结果图 展望 背影 现在生活，为节能减排，减少电能…
阅读更多...
推荐系统 FM因式分解

推荐系统 FM因式分解

reference：知乎 FM算法解析 LR算法没有二阶交叉 如果是id类特征，这里的x是0/1，raw的特征输入就是float，当然，在我的理解里，一般会把raw的特征进行分桶，还是映射到0/1特征，不然这个w…
阅读更多...
树莓派测试wifi与eth速率

树莓派测试wifi与eth速率

测试网速方法： 1.安装插件： 首先在树莓派端安装iperf3 sudo apt install iperf3PC端也需要安装iperf3，单击下面网址即可 下载网址 压缩包解压到桌面，文件内容如下图所示： 2.开始测速服务： 树莓派端在…
阅读更多...
周报终结者 GitLab 个人工作记录查询器

周报终结者 GitLab 个人工作记录查询器

序言 每周都要写周报，烦死人。为了解救自己，把自己从无聊的工作中抽离出来。 特别写了一个工具。可以查询GitLab中自己一段时间内的所有提交记录。 按照项目和分支进行排序 效果 还可以查询原始的json数据方便自己进行筛选和扩展 使用方式 1.获取个人…
阅读更多...
从 1 秒到 10 毫秒！在 APISIX 中减少 Prometheus 请求阻塞

从 1 秒到 10 毫秒！在 APISIX 中减少 Prometheus 请求阻塞

本文介绍了 Prometheus 插件造成长尾请求现象的原因，以及如何解决这个问题。 作者屠正松，Apache APISIX PMC Member。 原文链接 现象 在 APISIX 社区中，曾有部分用户陆续反馈一种神秘现象：部分请求延迟较长。具体表现为&#xf…
阅读更多...
Android电视盒子最强看电视app-tvbox配置(视频源)教程

Android电视盒子最强看电视app-tvbox配置(视频源)教程

今天给大家分享一下安卓tv上最强的看视频神器-tvbox的配置方法 tvbox是一款影视观看类的软件，各种影视资源都是为你免费提供的，还有海量热门影视为你提供电视直播，让你可以实时在线进行观看以及体验一样，超多影视剧内容你感兴趣的…
阅读更多...
实景建模整合了什么优势？有哪些领域应用？

实景建模整合了什么优势？有哪些领域应用？

近年来，无接触经济、线上营销模式成为了热门，伴随着国家十四五规划的出台，对数字经济的扶持是巨大的。VR实景迎来了发展新利好，实景建模—专业的倾斜摄影测量三维实景建模平台，为你真实还原现实世界！ 实景建…
阅读更多...
Homekit智能家居系列一智能触摸面板开关

Homekit智能家居系列一智能触摸面板开关

触摸开关，即通过触摸方式控制的墙壁开关，其感官场景如同我们的触屏手机，只需手指轻轻一点即可达到控制电器的目的，随着人们生活品质的提高，触摸开关将逐渐将换代传统机械按键开关。 触摸开关控制原理 触摸开关我们把…
阅读更多...
【Adobe】GenP3.0的使用教程

【Adobe】GenP3.0的使用教程

1、Google一下GenP 2、或者直接点击：https://www.reddit.com/r/GenP/ 3、选择GenP 3.0 - NEW 4、点击下载 注：这个地址可以不用科学上网即可下载：https://www.mediafire.com/file/jr0jqeynr4h21f9/Adobe_GenP_3.0.zip/file 5、点击运行 RunM…
阅读更多...
【并发基础】操作系统中线程/进程的生命周期与状态流转以及Java线程的状态流转详解

【并发基础】操作系统中线程/进程的生命周期与状态流转以及Java线程的状态流转详解

目录 一、操作系统中进程和线程的状态 1.1 进程 1.1.1 进程的概念 1.1.2 进程的状态 1.1.3 进程调度流程图（五状态） 1.1.4 挂起状态 1.1.4 进程调度流程图（六状态和七状态） 1.1.5 睡眠状态 1.1.6 进程的诞生与消亡 1.2 线程 1.2.1…
阅读更多...
运营新人必看 eBay申诉的最全资料

运营新人必看 eBay申诉的最全资料

eBay作为一个电商交易平台，限制还是不少的。前几篇eBay系列文章发布后，也有些兄弟来向我反应eBay平台的严格程度，很容易因为这样那样的原因就被封掉了，自己也莫名其妙的。龙哥今天就总结一下eBay封号中比较常见的原因和万一被封要…
阅读更多...
关于js数据类型的理解

关于js数据类型的理解

目录标题一、js数据类型分为 基本数据类型和引用数据类型二、区别：传值和传址三、深浅拷贝传值四、数据类型的判断一、js数据类型分为 基本数据类型和引用数据类型 1、基本数据类型 Number、String、Boolean、Null、undefined、BigInt、Symbol 2、引用数据类型 像对…
阅读更多...
详解信道估计的发展与最新研究进展（MIMO）

详解信道估计的发展与最新研究进展（MIMO）

目录 一. MIMO信道估计的重要性 二. 最经典的两种信道估计方法 2.1 最小二乘信道估计(LS) 2.2 最小均方误差信道估计(MMSE) 三. 优化传统的MIMO信道估计技术 四. 介绍压缩感知技术 五. 基于压缩感知的MIMO信道估计 5.1 压缩感知怎么用在MIMO信道估计 5.2 改进压缩感知…
阅读更多...
BIO,NIO,AIO

BIO,NIO,AIO

IO模型 用什么样的通道进行数据传输和接收，java支持3种io网络编程模式 BIO NIO AIO BIO 同步阻塞 一个客户端连接对应一个处理线程 BIO示例代码（客户端和服务端） package com.tuling.bio;import java.io.IOException; import java.net.So…
阅读更多...
WIFI P2P架构

WIFI P2P架构

WI-FI P2P定义架构3个组件组织结构技术标准P2P DiscoveryDevice Discovery（扫描）流程p2p probe 管理帧Group Formation（组网）GO Negotiation（GON）流程P2P Public Action管理帧Provision Discovery&#xff…
阅读更多...
Rust Web 进阶（一）：Rust异步编程（Tokio）

Rust Web 进阶（一）：Rust异步编程（Tokio）

这一篇将讲解什么是和为什么进行异步编程，Rust 怎么样进行异步编程以及其机制，并且讲解目前 rust 常用的异步编程的函数库。本章的内容来自杨旭老师的教程： https://www.bilibili.com/video/BV16r4y187P4/?spm_id_from333.999.0.0&vd_s…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023