⛄一、轴承故障分析简介
1 研究背景
滚动轴承故障占旋转机械故障的大约30%,现阶段主要采用信号分析来进行故障识别。探究形成机械设备故障尤其是滚动轴承的理论和诊断手段及方法是广大科学家们共同追求的目标,无论是在工程实际还是故障分析理论上都有着重大的意义和应用价值。
1.1 轴承诊断背景
(1)滚动轴承

图1 托辊实物图
滚动轴承是当前工业生产中应用频率最高的轴承,可以极大地有效的减少机械机构运转之间的摩擦损失,摩擦损失对于整个机械运转架构来说是很大的无效能,会造成很大的资源浪费,使得整个设计出的机械运转效率下降,增大使用成本。对于滚动轴承来说,滚动体的外形与尺寸及个数对滚动轴承的性能及使用寿命有着很大的影响,滚动轴承有着节能效果明显、维修简便,质量可靠等优点。同时采用滚动轴承维修量大大减少,有着维修简便的优点。
(2)轴承诊断
滚动轴承的故障诊断始于60年代,1966年瑞典SKF公司发明了用冲击脉冲仪检测轴承损伤,滚动轴承的故障诊断水平得到了很大的提高。
滚动轴承若故障会引起一定的的冲击振动,是由冲击点为原点以球面形式向外扩散,然后逐步通过相应机构如一些零件轴承座等传到箱体和机架。需要注意的是,因冲击产生的振动的为高频振动,在通过轴承构件传递振动时,会有比较明显的能量损失。因此,在轴承故障诊断中,所选取的试验点即测点应尽可能减少中间所经过的轴承构件,所选取的测试点离轴承外圈也就是冲击点的距离越小越好。根据通过产生异响和温度升高等异常现象,初步推断故障产生在轴承上,故布置3个测点位置如图,得到三段正常信号,三段故障信号。
表1 设备的一般参数


图2 测点布置图
通过查阅资料及经验推断,因设备故障发出的“沙沙”声,初步确定托辊故障发生在轴承上,滚动轴承安装在托辊内主要用以减少托辊的运行阻力及减少胶带的磨损。
根据给出的轴承信号,查到轴承基本信息如下表。
表2 SKF308/309轴承基本参数

(3)滚动轴承故障诊断方法
滚动轴承故障是运行过程中机械设备故障的主要原因之一。滑动轴承的失效形式有磨损失效,疲劳失效,腐蚀失效和气蚀失效。
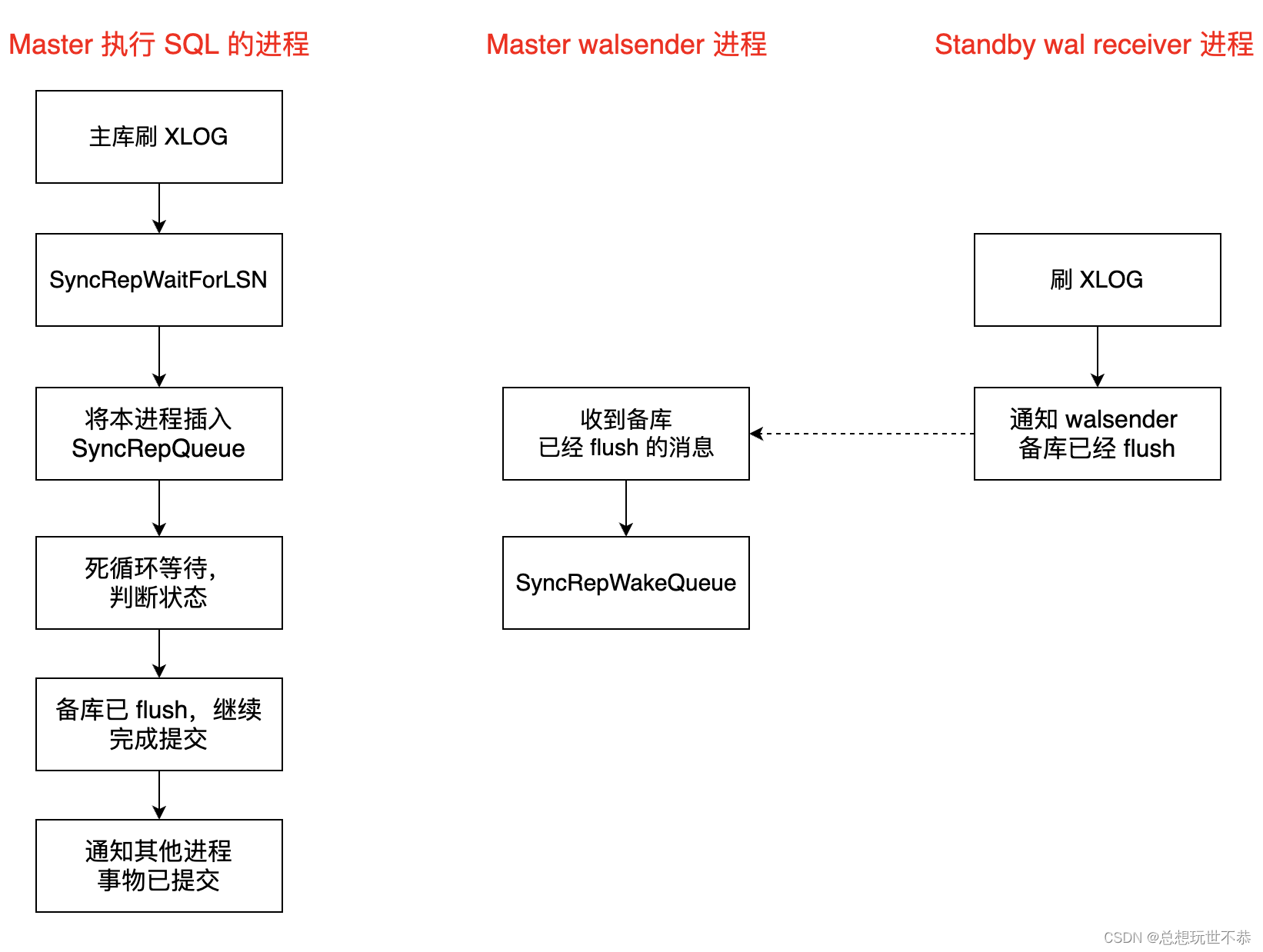
常用的对滚动轴承进行故障诊断的方式一般有时域分析,用时域参数对早期故障的敏感性,对滚动轴承进行定期检测,得到其峭度、峰值因子、以及振动频率有效值趋势曲线等,幅值或有效值的变化曲线或规律可以对滚动轴承故障有一个初步的诊断,或是频域分析,利用快速傅里叶变换获得振动信号的频谱图,了解频率成分。通过计算轴承故障频率与时域分析结果对比确定故障位置。
2 时域分析
2.1 时域波形分析
时域波形分析是指经过各种专业仪器采集记录并显示的被测设备信号与时间相对应的波形信号,如振动、噪声、温度、压力等进行分析,进而得到得到待测对象的时间历程的分析方法。信号在时域上的分析所包含的特征量较多,且视觉上更能明显看到规律,趋势也易于让人领会,是轴承故障诊断方面的重要依据。
表4 信号时域信息统计

通过对三个测点正常和故障的信号进行时域分析可以看出,故障信号的均值较正常信号均值要大,说明滚动体在滚道上运动的时候,不规则运动较大,轴承磨损程度大。故障信号较正常信号的方差值要大十倍左右,说明故障信号的数据波动程度很大。
每个测点的故障信号峰峰值比正常高很多,说明故障时机构振动、能量都很大。峭度对早期信号故障有较高的敏感性可以看出故障信号峭度比正常信号峭度大,说明轴承有一定程度的损伤。在一段故障信号中取三个幅值相同的点,w1信号周期约为0.4s,频率为2.5Hz,与滚动体故障频率接近。w2周期约为0.2s,频率约为5Hz与外圈故障频率接近。w3周期约为0.6s,频率为1.6Hz,与滚动体故障频率接近。
3 频谱分析
3.1 倒谱分析
倒谱分析就是将原始波形的傅里叶变换结进行对数求解,最后再将对数求解后的结果再进行傅里叶逆变换。倒谱分析在信轴承故障诊断方面具有较大的实用意义。倒谱分析可以将波形数据卷积后的多个信号进行分离,进而将波形数据中较为明显突出的特征量即特征信号分离出来,方便后面的对轴承的故障诊断分析,并将倒谱分析后的数据或波形特征与时域、频域等其他分析手段相结合进而达到对滚动轴承进行故障诊断的依据。

图5 第二段信号倒谱分析图
4 诊断结果与改进意见
通过对三个测点时域和频域的分析,由时域的周期性及计算出的轴承各部件故障频率分析,由时域分析总结分析出的故障信号特性及由频域分析对比总结出的的与轴承滚动体及外圈的故障数据特性相似性较大,初步推断是轴承滚动体和外圈由于点蚀、磨损等原因出现了裂纹等表面损伤性故障。
最后通过对轴承的拆解,发现轴承滚动体出现了磨损,轴承外圈出现了少部分点蚀,与本文诊断结果大致相符。
4.2 改进意见
为了预防轴承滚动体和外圈出现故障,应注意以下方面:
(1)注意在轴承装配之前的裂纹检查工作,若其装配前存在微裂纹、生锈等现象会导致轴承内各部件磨损过快,出现故障。
(2)注意轴承间各部件的润滑,控制润滑脂用量以达到最好的润滑效果。
⛄二、部分源代码
clear all;close all;clc
fs=20000; %采样频率
[fid1,message]=fopen('waiquan_10k_32768_7.5.dat','r');
[x,count1]=fscanf(fid1,'%f',32768);
fclose(fid1);
N=length(x);
f=fs*(0:N-1)/N; %频率分布
n=0:N-1;
t=n/fs; %时间序列
y=fft(x); %对原时域信号x进行fft,得到频域信号y
figure
plot(f,abs(y)) %绘制原信号的频谱y
xlabel('频率/Hz');
ylabel('振幅');
title('原信号频谱')
x2=hilbert(real(x1)); %x1的希尔伯特变换x2
x3=abs(x2); %x2取模,得到x3
%对x3进行fft,求包络谱
figure
plot((0:nfft-1)/nfft*fs,p) %绘制包络谱
xlabel('频率/Hz');
ylabel('振幅');
title('包络谱')
axis([0,1000,0,80]);
## ⛄三、运行结果


## ⛄四、matlab版本及参考文献
**1 matlab版本**
2014a
**2 参考文献**
[1] 严华,申雨.基于Matlab的轴承故障诊断分析[J].中国水运(下半月). 2021,21(02)
**3 备注**
简介此部分摘自互联网,仅供参考,若侵权,联系删除