1、IoU

1.1 什么是IOU

1.2 IOU代码

2、GIOU

2.1 为什么提出GIOU

2.2 GIoU代码

3 DIoU

3.1 为什么提出DIOU

3.2 DIOU代码

4 CIOU

4.1 为什么提出CIOU

4.2 CIOU代码

5 EIOU

5.1 为什么提出EIOU

5.2 EIOU代码

6 Wise-IoU

7 YOLOv5中添加GIoU、DIoU、CIoU、EIoU、Wise-IoU损失函数

1、IoU

1.1 什么是IOU

论文链接为：UnitBox: An Advanced Object Detection Network

IoU 的全称为交并比（Intersection over Union），通过这个名称我们大概可以猜到 IoU 的计算方法。IoU 计算的是 “预测的边框” 和 “真实的边框” 的交集和并集的比值。计算过程如下：

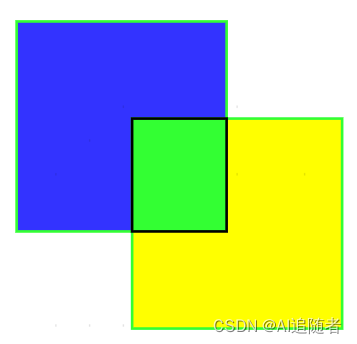
其中，绿色面积代表预测框B与真实框A的交集 $A\cap B$ ；则

$IOU=\frac{A\cap B}{A\cup B}$

显而易见，IOU的值越高也说明预测框与真实框重合程度越高，代表模型预测越准确，反之，IOU越低模型性能越差。

但是，IOU作为损失函数会出现以下问题：

如果两个框没有相交，根据定义，IoU=0，不能度量IoU为零距离远近的程度。同时因为loss=0，没有梯度回传，无法进行学习训练。
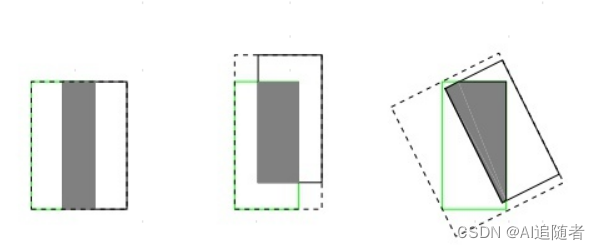
IoU无法精确的反映两者的重合度大小。如下图所示，三种情况IoU都相等，但看得出来他们的重合度是不一样的，左边的图回归的效果最好，右边的最差。

1.2 IOU代码

import numpy as np
def Iou(box1, box2, wh=False):
    if wh == False:
	    xmin1, ymin1, xmax1, ymax1 = box1
	    xmin2, ymin2, xmax2, ymax2 = box2
    else:
	    xmin1, ymin1 = int(box1[0]-box1[2]/2.0), int(box1[1]-box1[3]/2.0)
	    xmax1, ymax1 = int(box1[0]+box1[2]/2.0), int(box1[1]+box1[3]/2.0)
	    xmin2, ymin2 = int(box2[0]-box2[2]/2.0), int(box2[1]-box2[3]/2.0)
	    xmax2, ymax2 = int(box2[0]+box2[2]/2.0), int(box2[1]+box2[3]/2.0)
    # 获取矩形框交集对应的左上角和右下角的坐标（intersection）
    xx1 = np.max([xmin1, xmin2])
    yy1 = np.max([ymin1, ymin2])
    xx2 = np.min([xmax1, xmax2])
    yy2 = np.min([ymax1, ymax2])	
    # 计算两个矩形框面积
    area1 = (xmax1-xmin1) * (ymax1-ymin1) 
    area2 = (xmax2-xmin2) * (ymax2-ymin2)
    inter_area = (np.max([0, xx2-xx1])) * (np.max([0, yy2-yy1]))　#计算交集面积
    iou = inter_area / (area1+area2-inter_area+1e-6) 　#计算交并比

    return iou

2、GIOU

论文链接：Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression

2.1 为什么提出GIOU

为了解决上面两个问题，这篇论文提出了GIOU。由于IoU是比值的概念，对目标物体的scale是不敏感的。然而目标检测任务中的BBox的回归损失(MSE loss, l1-smooth loss等）优化和IoU优化不是完全等价的，而且 Ln 范数对物体的scale也比较敏感，IoU无法直接优化没有重叠的部分。这篇论文提出可以直接把IoU设为回归的loss。

GIOU的计算很简单，对于两个bounding box A和B。我们可以算出其最小凸集（同时包含了预测框和真实框的最小框的面积）C，有了最小凸集，就可以计算GIOU，如下所示

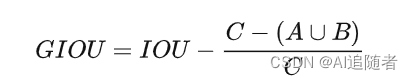
从公式可以看出，GIOU有几个优点：

GIOU是IOU的下界，且取值范围为(-1, 1]。当两个框不重合时，IOU始终为0，不论A、B相隔多远，但是对于GIOU来说，A，B不重合度越高（离的越远），GIOU越趋近于-1。
GIOU其实就是在IOU的基础上减掉了一个东西，这个减掉的东西，避免了两个bbox不重合时Loss为0的情况;
可导：这一点需要强调下，由于max，min，分段函数(比如ReLU)这些都是可导的，所以用1-GIOU作为Loss是可导的。
与IoU只关注重叠区域不同，GIoU不仅关注重叠区域，还关注其他的非重合区域，能更好的反映两者的重合度。

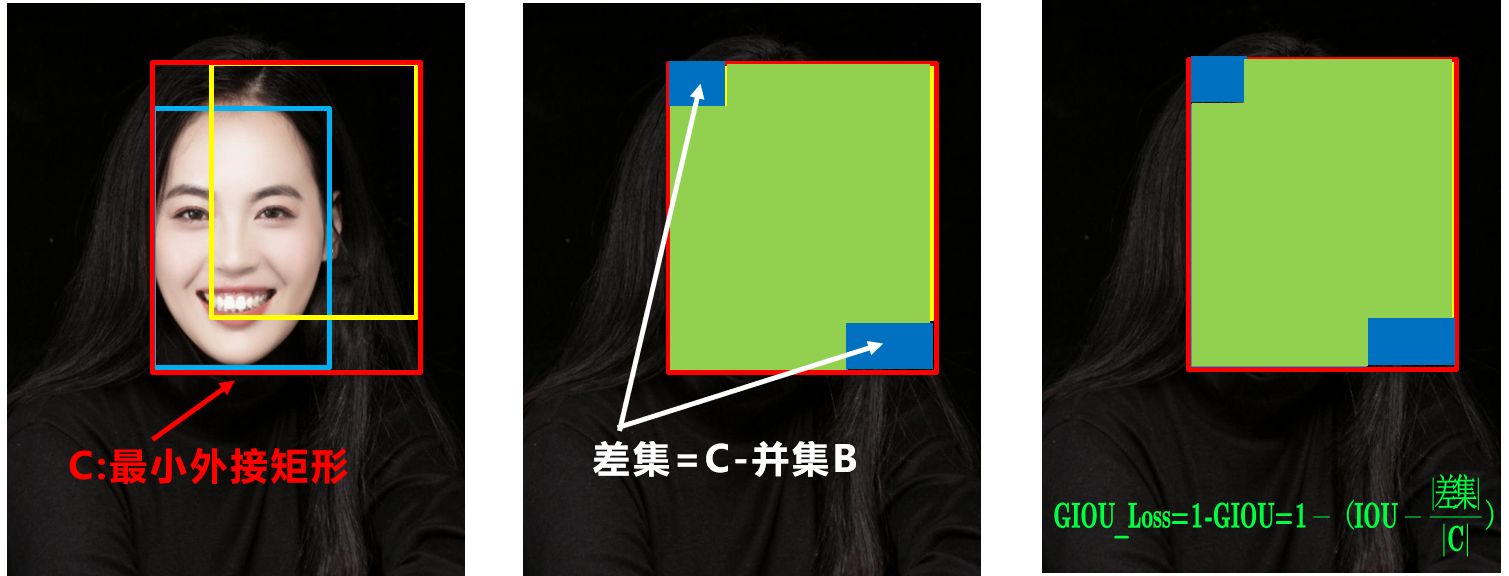
但是GIOU同样存在一些问题，主要有：

状态1、2、3都是预测框在目标框内部且预测框大小一致的情况，这时预测框和目标框的差集都是相同的，因此这三种状态的GIOU值也都是相同的，这时GIOU退化成了IOU，无法区分相对位置关系；
GIOU收敛较慢、回归不够准确。

2.2 GIoU代码

import numpy as np

def Giou_np(bbox_p, bbox_g):
    """
    :param bbox_p: predict of bbox(N,4)(x1,y1,x2,y2)
    :param bbox_g: groundtruth of bbox(N,4)(x1,y1,x2,y2)
    :return:
    """
    # for details should go to https://arxiv.org/pdf/1902.09630.pdf
    # ensure predict's bbox form
    x1p = np.minimum(bbox_p[:, 0], bbox_p[:, 2]).reshape(-1,1)
    x2p = np.maximum(bbox_p[:, 0], bbox_p[:, 2]).reshape(-1,1)
    y1p = np.minimum(bbox_p[:, 1], bbox_p[:, 3]).reshape(-1,1)
    y2p = np.maximum(bbox_p[:, 1], bbox_p[:, 3]).reshape(-1,1)

    bbox_p = np.concatenate([x1p, y1p, x2p, y2p], axis=1)
    # calc area of Bg
    area_p = (bbox_p[:, 2] - bbox_p[:, 0]) * (bbox_p[:, 3] - bbox_p[:, 1])
    # calc area of Bp
    area_g = (bbox_g[:, 2] - bbox_g[:, 0]) * (bbox_g[:, 3] - bbox_g[:, 1])

    # cal intersection
    x1I = np.maximum(bbox_p[:, 0], bbox_g[:, 0])
    y1I = np.maximum(bbox_p[:, 1], bbox_g[:, 1])
    x2I = np.minimum(bbox_p[:, 2], bbox_g[:, 2])
    y2I = np.minimum(bbox_p[:, 3], bbox_g[:, 3])
    I = np.maximum((y2I - y1I), 0) * np.maximum((x2I - x1I), 0)

    # find enclosing box
    x1C = np.minimum(bbox_p[:, 0], bbox_g[:, 0])
    y1C = np.minimum(bbox_p[:, 1], bbox_g[:, 1])
    x2C = np.maximum(bbox_p[:, 2], bbox_g[:, 2])
    y2C = np.maximum(bbox_p[:, 3], bbox_g[:, 3])

    # calc area of Bc
    area_c = (x2C - x1C) * (y2C - y1C)
    U = area_p + area_g - I
    iou = 1.0 * I / U

    # Giou
    giou = iou - (area_c - U) / area_c

    # loss_iou = 1 - iou loss_giou = 1 - giou
    loss_iou = 1.0 - iou
    loss_giou = 1.0 - giou
    return giou, loss_iou, loss_giou

# def giou_tf




if __name__ == '__main__':

    p = np.array([[21,45,103,172],
                  [34,283,155,406],
                  [202,174,271,255]])
    g = np.array([[59,106,154,230],
                  [71,272,191,419],
                  [257,244,329,351]])
    Giou_np(p, g)

3 DIoU

论文连接：Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression

3.1 为什么提出DIOU

一个好的目标框回归函数应该考虑三个重要几何因素：重叠面积、中心点距离，长宽比。

针对IOU和GIOU存在的问题，作者从两个方面进行考虑

如何最小化预测框和目标框之间的归一化距离？
如何在预测框和目标框重叠时，回归的更准确？

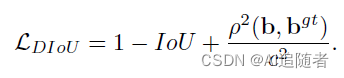
针对第一个问题，提出了DIOU_Loss（Distance_IOU_Loss）

DIOU_Loss考虑了重叠面积和中心点距离，当目标框包裹预测框的时候，直接度量2个框的距离，因此DIOU_Loss收敛的更快。DIOU损失的优点有：

与GIoU loss类似，DIoU loss在与目标框不重叠时，仍然可以为边界框提供移动方向。
DIoU loss可以直接最小化两个目标框的距离，因此比GIoU loss收敛快得多。
对于包含两个框在水平方向和垂直方向上这种情况，DIoU损失可以使回归非常快，而GIoU损失几乎退化为IoU损失。
DIoU还可以替换普通的IoU评价策略，应用于NMS中，使得NMS得到的结果更加合理和有效。

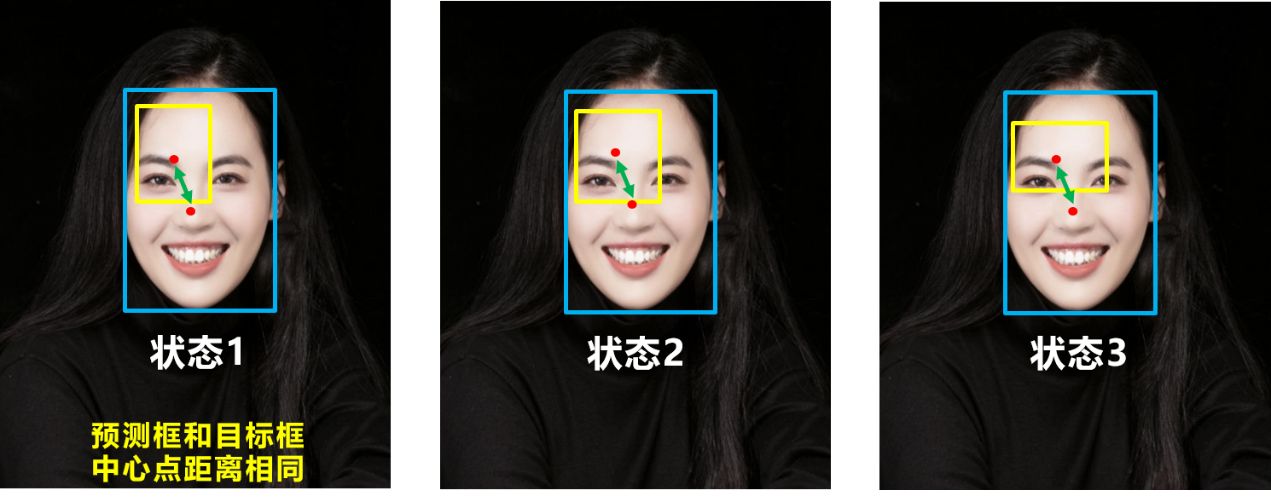
但DIOU同样存在缺点，那就是没有考虑到长宽比。比如下面三种情况，目标框包裹预测框，本来DIOU_Loss可以起作用。但预测框的中心点的位置都是一样的，因此按照DIOU_Loss的计算公式，三者的值都是相同的。

3.2 DIOU代码

def Diou(bboxes1, bboxes2):
    rows = bboxes1.shape[0]
    cols = bboxes2.shape[0]
    dious = torch.zeros((rows, cols))
    if rows * cols == 0:#
        return dious
    exchange = False
    if bboxes1.shape[0] > bboxes2.shape[0]:
        bboxes1, bboxes2 = bboxes2, bboxes1
        dious = torch.zeros((cols, rows))
        exchange = True
    # #xmin,ymin,xmax,ymax->[:,0],[:,1],[:,2],[:,3]
    w1 = bboxes1[:, 2] - bboxes1[:, 0]
    h1 = bboxes1[:, 3] - bboxes1[:, 1] 
    w2 = bboxes2[:, 2] - bboxes2[:, 0]
    h2 = bboxes2[:, 3] - bboxes2[:, 1]
    
    area1 = w1 * h1
    area2 = w2 * h2

    center_x1 = (bboxes1[:, 2] + bboxes1[:, 0]) / 2 
    center_y1 = (bboxes1[:, 3] + bboxes1[:, 1]) / 2 
    center_x2 = (bboxes2[:, 2] + bboxes2[:, 0]) / 2
    center_y2 = (bboxes2[:, 3] + bboxes2[:, 1]) / 2

    inter_max_xy = torch.min(bboxes1[:, 2:],bboxes2[:, 2:]) 
    inter_min_xy = torch.max(bboxes1[:, :2],bboxes2[:, :2]) 
    out_max_xy = torch.max(bboxes1[:, 2:],bboxes2[:, 2:]) 
    out_min_xy = torch.min(bboxes1[:, :2],bboxes2[:, :2])

    inter = torch.clamp((inter_max_xy - inter_min_xy), min=0)
    inter_area = inter[:, 0] * inter[:, 1]
    inter_diag = (center_x2 - center_x1)**2 + (center_y2 - center_y1)**2
    outer = torch.clamp((out_max_xy - out_min_xy), min=0)
    outer_diag = (outer[:, 0] ** 2) + (outer[:, 1] ** 2)
    union = area1+area2-inter_area
    dious = inter_area / union - (inter_diag) / outer_diag
    dious = torch.clamp(dious,min=-1.0,max = 1.0)
    if exchange:
        dious = dious.T
    return dious

4 CIOU

论文链接：Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression

4.1 为什么提出CIOU

CIOU论文考虑到bbox回归三要素中的长宽比还没被考虑到计算中，因此，进一步在DIoU的基础上提出了CIoU。其惩罚项如下面公式：

其中 $\alpha$ 是权重函数，而 $\nu$ 用来度量长宽比的相似性，定义为

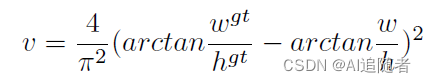
完整的CIOU损失函数定义：

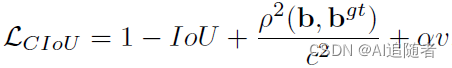
4.2 CIOU代码

def bbox_overlaps_ciou(bboxes1, bboxes2):
    rows = bboxes1.shape[0]
    cols = bboxes2.shape[0]
    cious = torch.zeros((rows, cols))
    if rows * cols == 0:
        return cious
    exchange = False
    if bboxes1.shape[0] > bboxes2.shape[0]:
        bboxes1, bboxes2 = bboxes2, bboxes1
        cious = torch.zeros((cols, rows))
        exchange = True

    w1 = bboxes1[:, 2] - bboxes1[:, 0]
    h1 = bboxes1[:, 3] - bboxes1[:, 1]
    w2 = bboxes2[:, 2] - bboxes2[:, 0]
    h2 = bboxes2[:, 3] - bboxes2[:, 1]

    area1 = w1 * h1
    area2 = w2 * h2

    center_x1 = (bboxes1[:, 2] + bboxes1[:, 0]) / 2
    center_y1 = (bboxes1[:, 3] + bboxes1[:, 1]) / 2
    center_x2 = (bboxes2[:, 2] + bboxes2[:, 0]) / 2
    center_y2 = (bboxes2[:, 3] + bboxes2[:, 1]) / 2

    inter_max_xy = torch.min(bboxes1[:, 2:],bboxes2[:, 2:])
    inter_min_xy = torch.max(bboxes1[:, :2],bboxes2[:, :2])
    out_max_xy = torch.max(bboxes1[:, 2:],bboxes2[:, 2:])
    out_min_xy = torch.min(bboxes1[:, :2],bboxes2[:, :2])

    inter = torch.clamp((inter_max_xy - inter_min_xy), min=0)
    inter_area = inter[:, 0] * inter[:, 1]
    inter_diag = (center_x2 - center_x1)**2 + (center_y2 - center_y1)**2
    outer = torch.clamp((out_max_xy - out_min_xy), min=0)
    outer_diag = (outer[:, 0] ** 2) + (outer[:, 1] ** 2)
    union = area1+area2-inter_area
    u = (inter_diag) / outer_diag
    iou = inter_area / union
    with torch.no_grad():
        arctan = torch.atan(w2 / h2) - torch.atan(w1 / h1)
        v = (4 / (math.pi ** 2)) * torch.pow((torch.atan(w2 / h2) - torch.atan(w1 / h1)), 2)
        S = 1 - iou
        alpha = v / (S + v)
        w_temp = 2 * w1
    ar = (8 / (math.pi ** 2)) * arctan * ((w1 - w_temp) * h1)
    cious = iou - (u + alpha * ar)
    cious = torch.clamp(cious,min=-1.0,max = 1.0)
    if exchange:
        cious = cious.T
    return cious

5 EIOU

论文链接：Focal and Efficient IOU Loss for Accurate Bounding Box Regression

5.1 为什么提出EIOU

CIOU Loss虽然考虑了边界框回归的重叠面积、中心点距离、纵横比。但是通过其公式中的v反映的纵横比的差异，而不是宽高分别与其置信度的真实差异，所以有时会阻碍模型有效的优化相似性，于是提出EIOU，它的主要思想是：

一是认为CIoU loss对于长宽比加入loss的设计不太合理，于是将CIoU loss中反应长宽比一致性的部分替换成了分别对于长和宽的一致性loss，形成了EIoU loss。
二是认为不太好的回归样本对回归loss产生了比较大的影响，回归质量相对较好的样本则难以进一步优化，所以论文提出Focal EIoU loss进行回归质量较好和质量较差的样本之间的平衡。

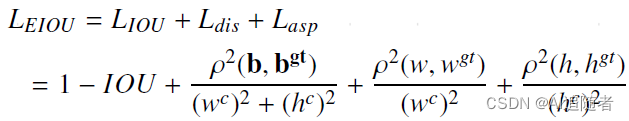
EIOU Loss优点：

1）将纵横比的损失项拆分成预测的宽高分别与最小外接框宽高的差值，加速了收敛提高了回归精度。
2）引入了Focal Loss优化了边界框回归任务中的样本不平衡问题，即减少与目标框重叠较少的大量锚框对BBox 回归的优化贡献，使回归过程专注于高质量锚框。

5.2 EIOU代码

def bbox_iou(box1, box2, x1y1x2y2=True, GIoU=False, DIoU=False, CIoU=False,  EIoU=False, eps=1e-7):
    # Returns the IoU of box1 to box2. box1 is 4, box2 is nx4
    box2 = box2.T

    # Get the coordinates of bounding boxes
    if x1y1x2y2:  # x1, y1, x2, y2 = box1
        b1_x1, b1_y1, b1_x2, b1_y2 = box1[0], box1[1], box1[2], box1[3]
        b2_x1, b2_y1, b2_x2, b2_y2 = box2[0], box2[1], box2[2], box2[3]
    else:  # transform from xywh to xyxy
        b1_x1, b1_x2 = box1[0] - box1[2] / 2, box1[0] + box1[2] / 2
        b1_y1, b1_y2 = box1[1] - box1[3] / 2, box1[1] + box1[3] / 2
        b2_x1, b2_x2 = box2[0] - box2[2] / 2, box2[0] + box2[2] / 2
        b2_y1, b2_y2 = box2[1] - box2[3] / 2, box2[1] + box2[3] / 2

    # Intersection area
    inter = (torch.min(b1_x2, b2_x2) - torch.max(b1_x1, b2_x1)).clamp(0) * \
            (torch.min(b1_y2, b2_y2) - torch.max(b1_y1, b2_y1)).clamp(0)

    # Union Area
    w1, h1 = b1_x2 - b1_x1, b1_y2 - b1_y1 + eps
    w2, h2 = b2_x2 - b2_x1, b2_y2 - b2_y1 + eps
    union = w1 * h1 + w2 * h2 - inter + eps

    iou = inter / union
    if GIoU or DIoU or CIoU or EIoU:
        cw = torch.max(b1_x2, b2_x2) - torch.min(b1_x1, b2_x1)  # convex (smallest enclosing box) width
        ch = torch.max(b1_y2, b2_y2) - torch.min(b1_y1, b2_y1)  # convex height
        if CIoU or DIoU or EIoU:  # Distance or Complete IoU https://arxiv.org/abs/1911.08287v1
            c2 = cw ** 2 + ch ** 2 + eps  # convex diagonal squared
            rho2 = ((b2_x1 + b2_x2 - b1_x1 - b1_x2) ** 2 +
                    (b2_y1 + b2_y2 - b1_y1 - b1_y2) ** 2) / 4  # center distance squared
            if DIoU:
                return iou - rho2 / c2  # DIoU
            elif CIoU:  # https://github.com/Zzh-tju/DIoU-SSD-pytorch/blob/master/utils/box/box_utils.py#L47
                v = (4 / math.pi ** 2) * torch.pow(torch.atan(w2 / h2) - torch.atan(w1 / h1), 2)
                with torch.no_grad():
                    alpha = v / (v - iou + (1 + eps))
                return iou - (rho2 / c2 + v * alpha)  # CIoU
            elif EIoU:
                rho_w2 = ((b2_x2 - b2_x1) - (b1_x2 - b1_x1)) ** 2
                rho_h2 = ((b2_y2 - b2_y1) - (b1_y2 - b1_y1)) ** 2
                cw2 = cw ** 2 + eps
                ch2 = ch ** 2 + eps
                return iou - (rho2 / c2 + rho_w2 / cw2 + rho_h2 / ch2)
        else:  # GIoU https://arxiv.org/pdf/1902.09630.pdf
            c_area = cw * ch + eps  # convex area
            return iou - (c_area - union) / c_area  # GIoU
    else:
        return iou  # IoU

6 Wise-IoU

论文链接：Wise-IoU: Bounding Box Regression Loss with Dynamic Focusing Mechanism

具体关于Wise-IoU损失的介绍请参考前期博客

优化改进YOLOv5算法之Wise-IOU损失函数_yolov5算法优化_AI追随者的博客-CSDN博客

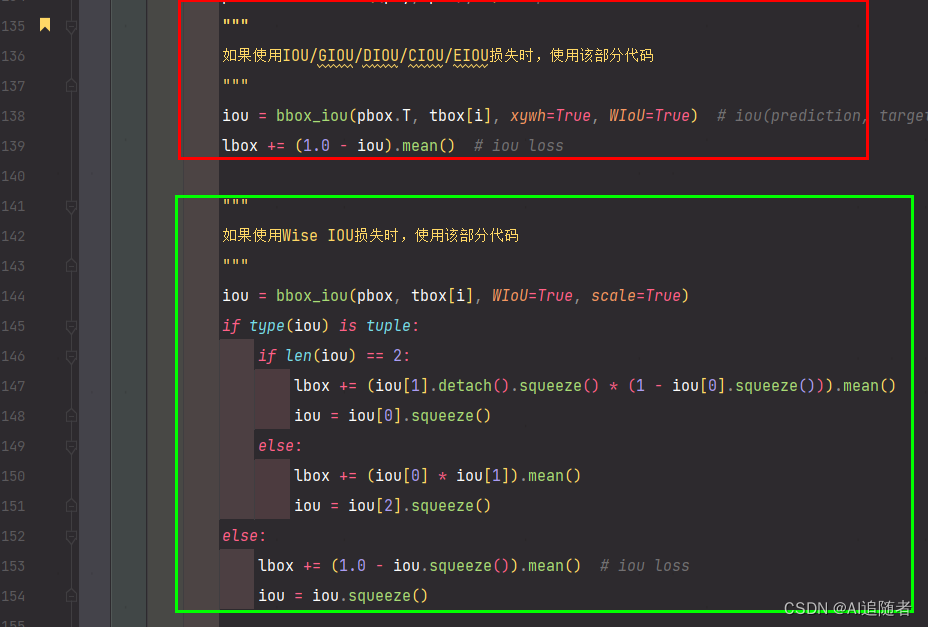
7 YOLOv5中添加GIoU、DIoU、CIoU、EIoU、Wise-IoU损失函数

yolov5-6.1版本中的iou损失函数是在utils/metrics.py文件定义的，在该文件添加以下关于GIoU、DIoU、CIoU、EIoU、Wise-IoU函数的代码，如下所示

import numpy as np
import torch, math
 
class WIoU_Scale:
    ''' monotonous: {
            None: origin v1
            True: monotonic FM v2
            False: non-monotonic FM v3
        }
        momentum: The momentum of running mean'''
    
    iou_mean = 1.
    monotonous = False
    _momentum = 1 - 0.5 ** (1 / 7000)
    _is_train = True
 
    def __init__(self, iou):
        self.iou = iou
        self._update(self)
    
    @classmethod
    def _update(cls, self):
        if cls._is_train: cls.iou_mean = (1 - cls._momentum) * cls.iou_mean + \
                                         cls._momentum * self.iou.detach().mean().item()
    
    @classmethod
    def _scaled_loss(cls, self, gamma=1.9, delta=3):
        if isinstance(self.monotonous, bool):
            if self.monotonous:
                return (self.iou.detach() / self.iou_mean).sqrt()
            else:
                beta = self.iou.detach() / self.iou_mean
                alpha = delta * torch.pow(gamma, beta - delta)
                return beta / alpha
        return 1
    
 
def bbox_iou(box1, box2, xywh=True, GIoU=False, DIoU=False, CIoU=False, SIoU=False, EIoU=False, WIoU=False, Focal=False, alpha=1, gamma=0.5, scale=False, eps=1e-7):
    # Returns Intersection over Union (IoU) of box1(1,4) to box2(n,4)
 
    # Get the coordinates of bounding boxes
    if xywh:  # transform from xywh to xyxy
        (x1, y1, w1, h1), (x2, y2, w2, h2) = box1.chunk(4, -1), box2.chunk(4, -1)
        w1_, h1_, w2_, h2_ = w1 / 2, h1 / 2, w2 / 2, h2 / 2
        b1_x1, b1_x2, b1_y1, b1_y2 = x1 - w1_, x1 + w1_, y1 - h1_, y1 + h1_
        b2_x1, b2_x2, b2_y1, b2_y2 = x2 - w2_, x2 + w2_, y2 - h2_, y2 + h2_
    else:  # x1, y1, x2, y2 = box1
        b1_x1, b1_y1, b1_x2, b1_y2 = box1.chunk(4, -1)
        b2_x1, b2_y1, b2_x2, b2_y2 = box2.chunk(4, -1)
        w1, h1 = b1_x2 - b1_x1, (b1_y2 - b1_y1).clamp(eps)
        w2, h2 = b2_x2 - b2_x1, (b2_y2 - b2_y1).clamp(eps)
 
    # Intersection area
    inter = (b1_x2.minimum(b2_x2) - b1_x1.maximum(b2_x1)).clamp(0) * \
            (b1_y2.minimum(b2_y2) - b1_y1.maximum(b2_y1)).clamp(0)
 
    # Union Area
    union = w1 * h1 + w2 * h2 - inter + eps
    if scale:
        self = WIoU_Scale(1 - (inter / union))
 
    # IoU
    # iou = inter / union # ori iou
    iou = torch.pow(inter/(union + eps), alpha) # alpha iou
    if CIoU or DIoU or GIoU or EIoU or SIoU or WIoU:
        cw = b1_x2.maximum(b2_x2) - b1_x1.minimum(b2_x1)  # convex (smallest enclosing box) width
        ch = b1_y2.maximum(b2_y2) - b1_y1.minimum(b2_y1)  # convex height
        if CIoU or DIoU or EIoU or SIoU or WIoU:  # Distance or Complete IoU https://arxiv.org/abs/1911.08287v1
            c2 = (cw ** 2 + ch ** 2) ** alpha + eps  # convex diagonal squared
            rho2 = (((b2_x1 + b2_x2 - b1_x1 - b1_x2) ** 2 + (b2_y1 + b2_y2 - b1_y1 - b1_y2) ** 2) / 4) ** alpha  # center dist ** 2
            if CIoU:  # https://github.com/Zzh-tju/DIoU-SSD-pytorch/blob/master/utils/box/box_utils.py#L47
                v = (4 / math.pi ** 2) * (torch.atan(w2 / h2) - torch.atan(w1 / h1)).pow(2)
                with torch.no_grad():
                    alpha_ciou = v / (v - iou + (1 + eps))
                if Focal:
                    return iou - (rho2 / c2 + torch.pow(v * alpha_ciou + eps, alpha)), torch.pow(inter/(union + eps), gamma)  # Focal_CIoU
                else:
                    return iou - (rho2 / c2 + torch.pow(v * alpha_ciou + eps, alpha))  # CIoU
            elif EIoU:
                rho_w2 = ((b2_x2 - b2_x1) - (b1_x2 - b1_x1)) ** 2
                rho_h2 = ((b2_y2 - b2_y1) - (b1_y2 - b1_y1)) ** 2
                cw2 = torch.pow(cw ** 2 + eps, alpha)
                ch2 = torch.pow(ch ** 2 + eps, alpha)
                if Focal:
                    return iou - (rho2 / c2 + rho_w2 / cw2 + rho_h2 / ch2), torch.pow(inter/(union + eps), gamma) # Focal_EIou
                else:
                    return iou - (rho2 / c2 + rho_w2 / cw2 + rho_h2 / ch2) # EIou
            elif SIoU:
                # SIoU Loss https://arxiv.org/pdf/2205.12740.pdf
                s_cw = (b2_x1 + b2_x2 - b1_x1 - b1_x2) * 0.5 + eps
                s_ch = (b2_y1 + b2_y2 - b1_y1 - b1_y2) * 0.5 + eps
                sigma = torch.pow(s_cw ** 2 + s_ch ** 2, 0.5)
                sin_alpha_1 = torch.abs(s_cw) / sigma
                sin_alpha_2 = torch.abs(s_ch) / sigma
                threshold = pow(2, 0.5) / 2
                sin_alpha = torch.where(sin_alpha_1 > threshold, sin_alpha_2, sin_alpha_1)
                angle_cost = torch.cos(torch.arcsin(sin_alpha) * 2 - math.pi / 2)
                rho_x = (s_cw / cw) ** 2
                rho_y = (s_ch / ch) ** 2
                gamma = angle_cost - 2
                distance_cost = 2 - torch.exp(gamma * rho_x) - torch.exp(gamma * rho_y)
                omiga_w = torch.abs(w1 - w2) / torch.max(w1, w2)
                omiga_h = torch.abs(h1 - h2) / torch.max(h1, h2)
                shape_cost = torch.pow(1 - torch.exp(-1 * omiga_w), 4) + torch.pow(1 - torch.exp(-1 * omiga_h), 4)
                if Focal:
                    return iou - torch.pow(0.5 * (distance_cost + shape_cost) + eps, alpha), torch.pow(inter/(union + eps), gamma) # Focal_SIou
                else:
                    return iou - torch.pow(0.5 * (distance_cost + shape_cost) + eps, alpha) # SIou
            elif WIoU:
                if Focal:
                    raise RuntimeError("WIoU do not support Focal.")
                elif scale:
                    return getattr(WIoU_Scale, '_scaled_loss')(self), (1 - iou) * torch.exp((rho2 / c2)), iou # WIoU https://arxiv.org/abs/2301.10051
                else:
                    return iou, torch.exp((rho2 / c2)) # WIoU v1
            if Focal:
                return iou - rho2 / c2, torch.pow(inter/(union + eps), gamma)  # Focal_DIoU
            else:
                return iou - rho2 / c2  # DIoU
        c_area = cw * ch + eps  # convex area
        if Focal:
            return iou - torch.pow((c_area - union) / c_area + eps, alpha), torch.pow(inter/(union + eps), gamma)  # Focal_GIoU https://arxiv.org/pdf/1902.09630.pdf
        else:
            return iou - torch.pow((c_area - union) / c_area + eps, alpha)  # GIoU https://arxiv.org/pdf/1902.09630.pdf
    if Focal:
        return iou, torch.pow(inter/(union + eps), gamma)  # Focal_IoU
    else:
        return iou  # IoU

然后在utils/loss.py文件中调用bbox_iou损失函数时，将对应的IOU设置为True即可。