定义
对于相同的训练样本,不同学习算法会产生不同的模型,决定其产生模型的,是学习算法本身的“偏好”。此处,书中引入“归纳偏好”的概念:
机器学习算法在学习过程中对某种类型假设的偏好,称为"归纳偏好",或简称为"偏好"。
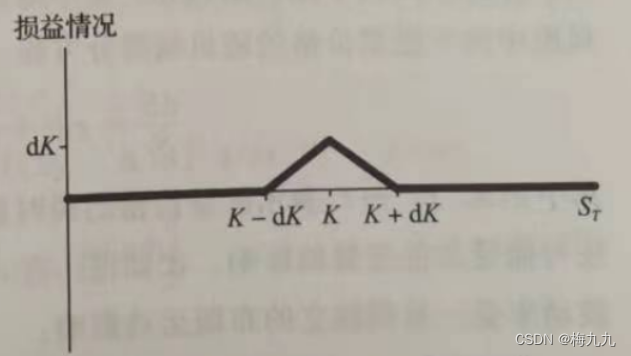
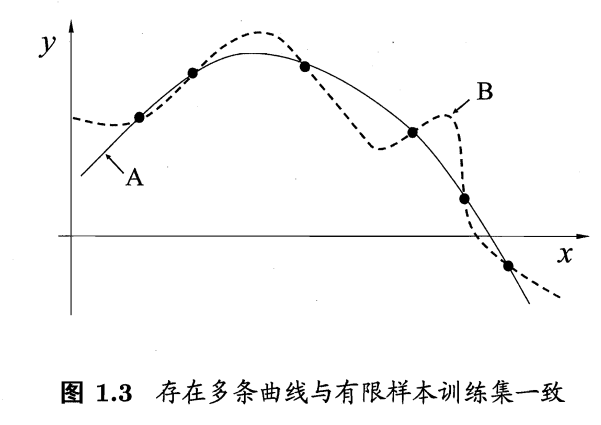
归纳偏好的作用在回归学习中可能更直观(如下图所示)。这里的每个训练样本是图中的一个点 (x,y),要学得一个与训练集一致的模型,相当于找到一条穿过所有训练样本点的曲线.显然,对有限个样本点组成的训练集,存在着很多条曲线与其一致.我们的学习算法必须有某种偏好,才能产出它认为"正确"的模型。
判别原则
此处,我们引入两种判别原则:
奥卡姆剃刀原则
"奥卡姆剃刀" (Occam's razor) 是一种常用的、自然科学研究中最基本的原则,即"若有多个假设与观察一致,则选最简单的那个。
如果采用这个原则,并且假设我们认为"更平滑"意味着"更简单" ,则在上例中我们会自然地偏好"平滑"的曲线 A。
但在实际应用中,归纳偏好对应了学习算法本身所做出的关于"什么样的模型更好"的假设,这个假设是否成立,即算法的归纳偏好是否与问题本身匹配,大多数时候直接决定了算法能否取得好的性能。
例如,对于下面的两个图像,a图中,平滑的A曲线更符合测试样本,这与奥卡姆剃刀原则相符;
但在b图中,“崎岖复杂”的B曲线更符合测试样本,这就并不符合奥卡姆剃刀原则。
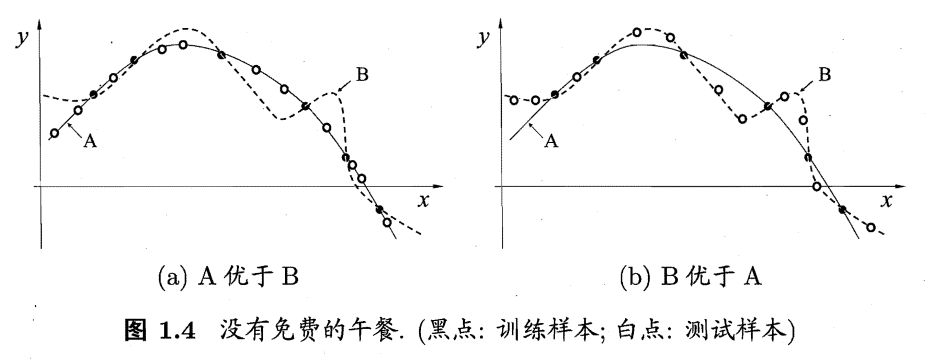
故,我们可以看出,算法的优劣是根据实际问题判定。尽管A曲线更符合我们对“泛化能力强的好算法”的认知,但也存在与B曲线更符合的实际问题。
换言之,对于一个学习算法A,若它在某些问题上比学习算法B好,则必然存在另一些问题,在那里,B比 A 好。
NFL定理(“没有免费的午餐”定理)
对于两个不同的学习算法A和B,无论学习算法A多聪明,学习算法B多笨拙,它们的期望性能都相同。
(对于此定理,书中给出了证明,但限于我浅薄的数学知识,目前我尚不能完全理解,故此处仅将书中证明过程附上,不做具体解释,日后再补全)

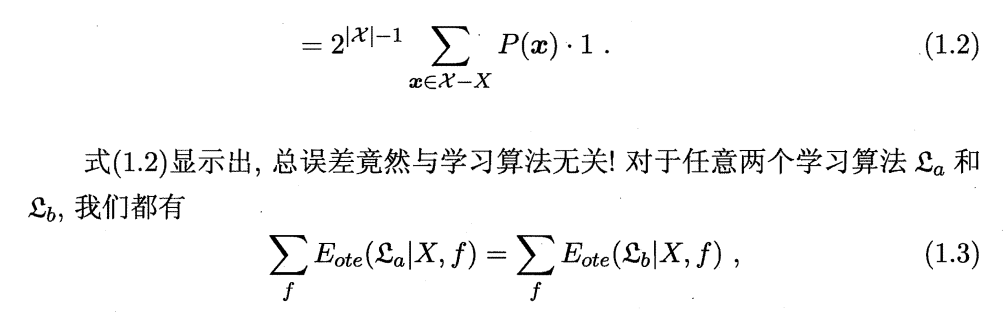
需要注意的是,NFL 定理有一个重要前提:所有"问题"出现的机会相同、或所有问题同等重要。但实际情形并不是这样。但很多时候,我们只关注自己正在试图解决的问题(例如某个具体应用任务),希望为它找到一个解决方案,至于这个解决方案在别的问题、甚至在相似的问题上是否为好方案,我们并不关心。
NFL 定理最重要的寓意,是让我们清楚地认识到,脱离具体问题,空泛地谈论"什么学习算法更好"毫无意义。要谈论算法的相对优劣,必须要针对具体的学习问题,学习算法自身的归纳偏好与问题是否相配,往往会起到决定性的作用。