基本术语
机器学习正是这样一门学科,它致力于研究如何通过计算的手段,利用经 验来玫善系统自身的性能在计算机系统中,"经验"通常以"数据"形式存 在,因此,机器学习所研究的主要内容,是关于在计算机上从数据中产生"模 型"的算法,即"学习算法"。 有了学习算法,我 们把经验数据提供给它,它就能基于这些数据产生模型;在面对新的情况时,模型会给我们提供相应的判断。
这组记录的集合称为一个"数据集" ,
其中每条记录是关于一 个事件或对象的描述,称为一个"示例" 或"样 本" ,
反映事件或对象在某方面的表现或性质的事项,称为"属性"或"特征", 属性上的取 值,称为"属性值",
属性张成的空 间称为"属性空间""样本空间" 或"输入 空间",
如果我们把三种属性作为三个坐标轴,则它们张成 一个用于描述XX的三维空间,每个XX都可在这个空间中找到自己的坐标位 置.由于空间中的每个点对应一个坐标向量,因此我们也把一个示例称为一个 "特征向量" 。
从数据中学得模型的过程称为"学习"或"训练" , 这个过程通过执行某个学习算法来完成,
训练过程中使用的数据称为"训练 数据" ,其中每个样本称为一个训练样本" ,
训练样本组成的集合称为"训练集",
学得模型对应了关于数据 的某种潜在的规律,因此亦称"假设" ,
这种潜在规律自身,则称 为"真相"或"真实" ,学习过程就是为了找出或逼近真相。
本 书有时将模型称为"学习器" ,可看作学习算法在给定数据和参数空 间上的实例化.
要建立这样的关于"预测" 模型,我们需获得训练样本的"结果"信息,例如" ((色泽=青绿;根蒂=蜷缩; 敲声=浊响),好瓜)"
这里关于示例结果的信息,例如"好瓜",称为"标 记" ,
拥有了标记信息的示例,则称为"样例" ,
一般地,用(xi yi) 表示第 i个样例 其中 yi∈Y 是示例 xi 的标记,Y是所有标记的集合, 亦称"标记空间" 或"输出空间" 。
若我们欲预测的是离散值,例如"好瓜" "坏瓜",此类学习任务称为 "分类" ;
若欲预测的是连续值,例如西瓜成熟度 0.95 0.37 此类学习任务称为"回归".
对只涉及两个类别的"二分 类"任务,通常称其中一个类为 "正类" ,另一个类为"反类";涉及多个类别时,则称为"多分 类"任务。
学得模型后,使用其母行预测的过程称为"测试" (testing) ,被预测的样本 称为"测试样本" , "聚类",即将训练集中的西瓜分成若干 组,每组称为一个"簇" (cluster); 这些自动形成的簇可能对应一些潜在的概念 划分,例如"浅色瓜" "深色瓜 ",这样的学习过程有助于我们了解数据内在的规律,能为更深入地分析数据建立基础。需说明 的是,在聚类学习中,"浅色瓜" "本地瓜"这样的概念我们事先是不知道的, 而且学习过程中使用的训练样本通常不拥有标记信息。 根据训练数据是否拥有标记信息,学习任务可大致划分为两大类"监督 学习"和"无监督学习",分类和回归是前者的代表,而聚类则是后者的代表。
学得模型适用于新样本的能力,称为"泛化" 能力.
通常假设样本空间中全 体样本服从一个未知"分布"D, 我们获得的每个样本都是独立 地从这个分布上采样获得的,即"独立同分布"。一般而言,训练样本越多,我们得到的关于D的信息越多,这样就越有可能通过学习获得具有强泛化能力的模型.
假设空间
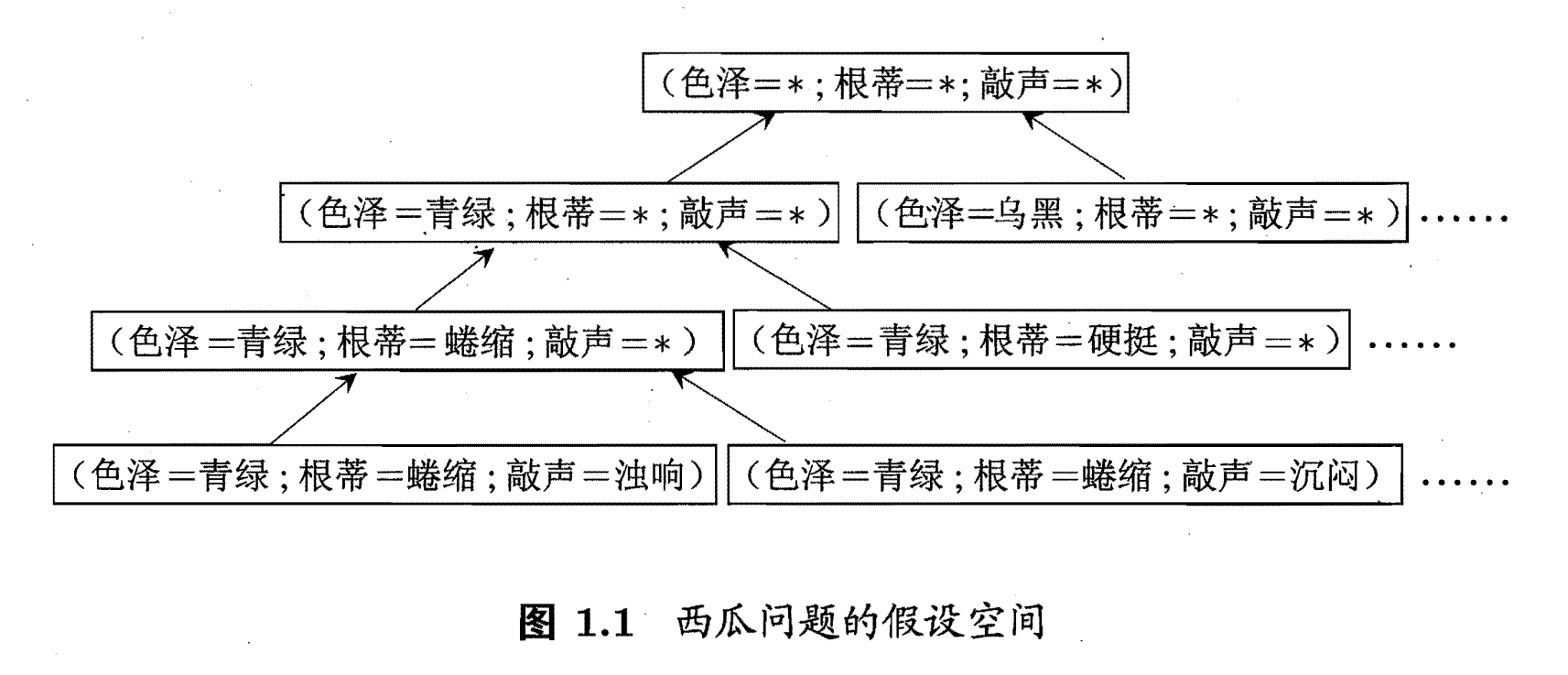
我们可以把学习过程看作一个在所有假设组成的空间中进行搜索的过程,搜索目标是找到与训练集"匹配" 的假设,即能够将训练集中的瓜判断正确的假设.假设的表示一旦确定,假设空间及其规模大小就确定了.
对于西瓜问题,这里我们的假设空间由形如"(色泽=?)^(根蒂=?) ^ (敲声=?)"的可能取值所形成的假设组成.

例如色泽有"青绿" "乌黑" "浅白"这三种可能取值;
还需考虑到,也许"色泽"无论取什么值都合适,我们用通符"*"来表示,例如"好瓜件(色泽= *) ^ (根蒂口蜷缩)八(敲声=浊响)" ,即"好瓜是根蒂蜷缩、敲声浊响的瓜,什么色泽都行"
此外,还需考虑极端情况:有可能"好瓜"这个概念根本就不成立,世界上没有"好瓜"这种东西;我们用∅表示这个假设.
这样,若"色泽" "根蒂" "敲声"分别有 3,3,2种可能取值,则我们面临的假设空间规模大小为4 x 3 x 3 + 1 = 37
(4,3,3分别代表"色泽" "根蒂" "敲声"的取值,除特征取值外,还可以取“*”,最后的1代表∅,即不存在好瓜)