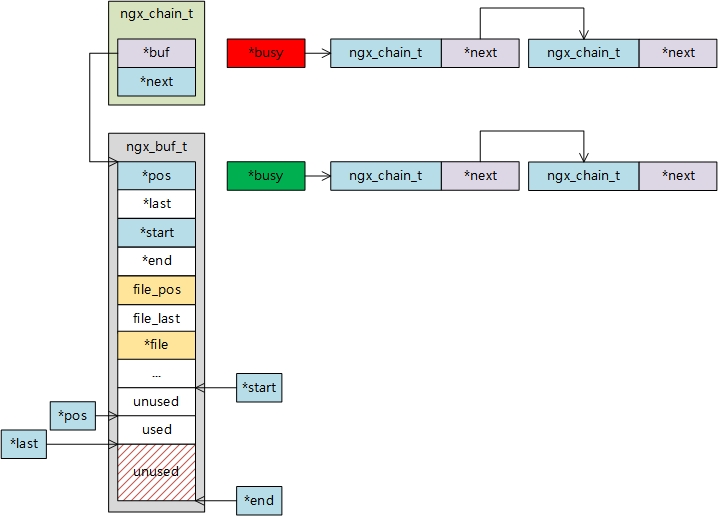
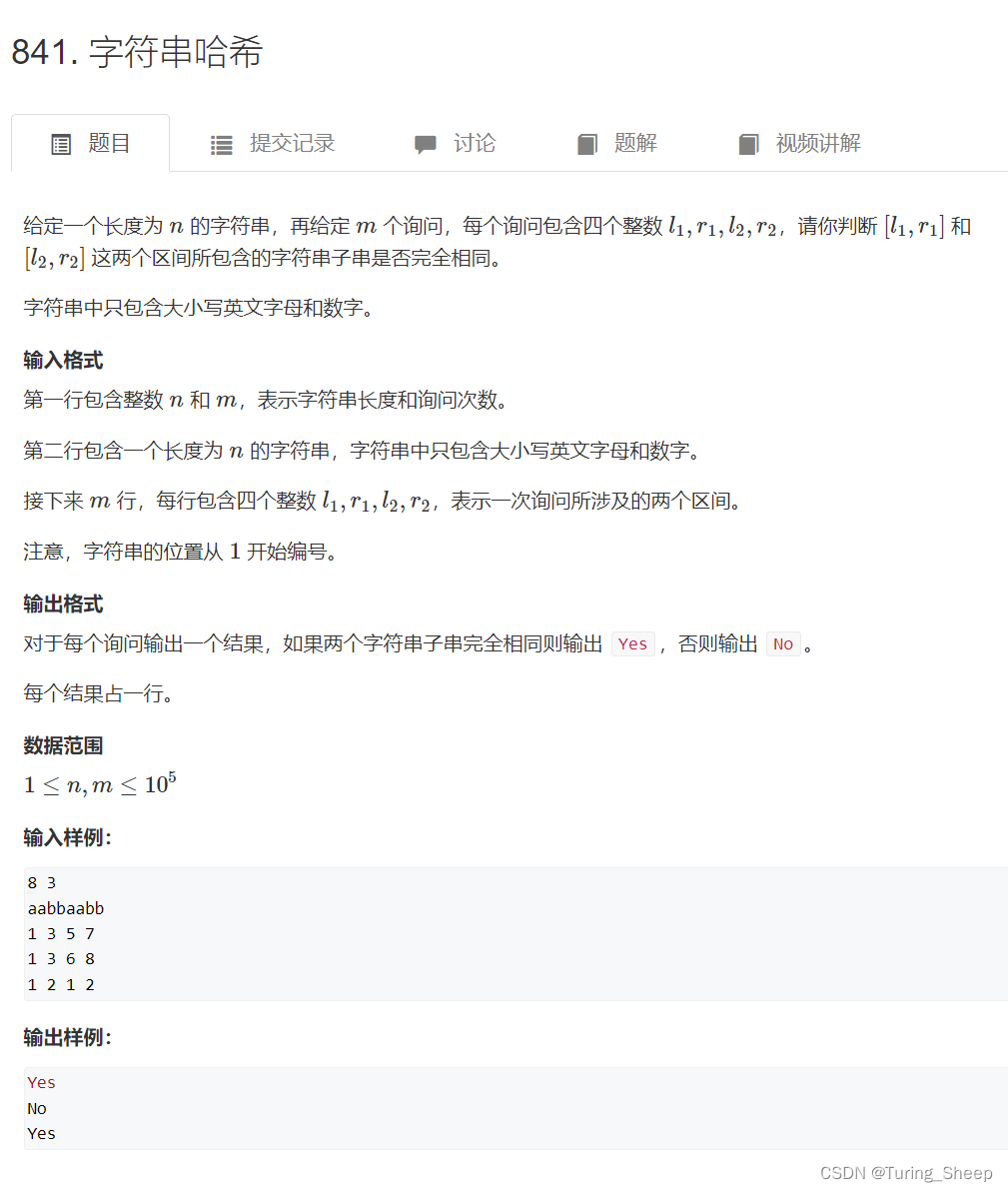
文章目录
- 利用朴素贝叶斯进行文档分类
- 1、获取数据集
- 2、切分文本
- 3、构建词表和分类
- 4、构建分类器
- 5、测试算法
- 利用朴素贝叶斯进行垃圾邮件过滤
- 1、导入数据集
- 2、垃圾邮件预测
- 总结
利用朴素贝叶斯进行文档分类
1、获取数据集
下载数据集,获取到一些邮件文档。其中ham文件夹下都是正常邮件,spam下都是垃圾邮件。

数据集中将一些词组用空格分开,方便后面分割词组,统计词表。

2、切分文本
每一份邮件里面用空格键分割出很多的词组,需要将这些词组分割出来,放在一个词表里面。
def cut_sentences(content): # 实现分句的函数,content参数是传入的文本字符串
end_flag = ['?', '!', '.', '?', '!', '。', ' '] # 结束符号,包含中文和英文的
content_len = len(content)
sentences = [] # 存储每一个句子的列表
tmp_char = ''
for idx, char in enumerate(content):
tmp_char += char # 拼接字符
if (idx + 1) == content_len: # 判断是否已经到了最后一位
sentences.append(tmp_char.strip().replace('\ufeff', ''))
break
if char in end_flag: # 判断此字符是否为结束符号
# 再判断下一个字符是否为结束符号,如果不是结束符号,则切分句子
next_idx = idx + 1
if not content[next_idx] in end_flag:
sentences.append(tmp_char.strip().replace('\ufeff', ''))
tmp_char = ''
sentences = list(set(sentences))
return [tok for tok in sentences if len(tok) > 1]
words = cut_sentences(open('TrainingSet/Ham/{}.txt'.format(2)).read())
print(words)
例如分割好一份邮件后,可以得到一个词表

3、构建词表和分类
下面方法中,posting_list 存放着每一个邮件的词表,class_vec 里面存放对应下标词表的类别,1代表友好文件,0代表不友好文件。最后返回一个词表的列表,和一个类别的列表。
# 获取词表和对应类别
def load_data_set():
# 词表和对应类别
posting_list = []
class_vec = []
for i in range(2, 10):
# 获取友好邮件词表
words = cut_sentences(open('TrainingSet/Ham/{}.txt'.format(i)).read())
posting_list.append(words)
class_vec.append(1)
# 获取不友好邮件词表
words = cut_sentences(open('TrainingSet/Spam/{}.txt'.format(i)).read())
posting_list.append(words)
class_vec.append(0)
return posting_list, class_vec

create_vocab_list方法会将load_data_set返回的词表列表合并成一个大的词表,里面每一个词组输给Set函数后,set会返回一个不重复的大词表。
# 合并所有词表
def create_vocab_list(data_set):
vocab_set = set()
for item in data_set:
# | 求两个集合的并集
vocab_set = vocab_set | set(item)
return list(vocab_set)
print(create_vocab_list(posting_list))
通过上面create_vocab_list方法可以返回一个包含所有词汇的大词表,用set_of_words2vec方法,传入大词表与小词表,可以遍历出小词表中每个词汇在大词表中存在的位置,对应位置标志置为1。创建一个和词汇表等长的向量,并将其元素都设置为0,遍历文档中的所有单词,如果出现了词汇表中的单词,则将输出的文档向量中的对应值设为1。
def set_of_words2vec(vocab_list, input_set):
# 创建一个和词汇表等长的向量,并将其元素都设置为0
result = [0] * len(vocab_list)
# 遍历文档中的所有单词,如果出现了词汇表中的单词,则将输出的文档向量中的对应值设为1
for word in input_set:
if word in vocab_list:
result[vocab_list.index(word)] = 1
else:
pass
return result

4、构建分类器
利用公式:
P
(
c
i
∣
w
)
=
P
(
w
∣
c
i
)
P
(
c
i
)
P
(
w
)
P(c_{i}|\mathbf{w } ) = \frac{P(\mathbf{w }|c_{i})P(c_{i})}{P(\mathbf{w } )}
P(ci∣w)=P(w)P(w∣ci)P(ci)
首先可以通过类别i(友好或者非友好)邮件数除以总的邮件数计算概率P(ci)。接着计算P(w|ci),这里就要用到贝叶斯假设。如果将w展开为一个个独立特征,那么就可以将上述概率写作P(w0,w1,w2...wn),这里假设所有词都互相独立,该假设也作为条件独立性假设,它意味着可以使用P(w0,ci)P(w1,ci)P(w2,ci)...P(wn,ci)计算概率。
该函数的伪代码如下:
计算每个类别中的文档数目
对每篇训练文档:
对每个类别:
如果词条出现在文档中→ 增加该词条的计数值
增加所有词条的计数值
对每个类别:
对每个词条:
将该词条的数目除以总词条数目得到条件概率
返回每个类别的条件概率
计算P(wi|c1)和P(wi|c1),需要初始化程序中的分子变量和分母变量。一旦每个词语(友好或者不友好)在某一文件中出现,则改词对应的个数(p0Num或者p1Num)就加1,而在所有文件中,该文件总词数也对应加1。
def train_naive_bayes(train_mat, train_category):
train_doc_num = len(train_mat)
words_num = len(train_mat[0])
# 因为侮辱性的被标记为了1, 所以只要把他们相加就可以得到侮辱性的有多少
# 侮辱性文件的出现概率,即train_category中所有的1的个数,
# 代表的就是多少个侮辱性文件,与文件的总数相除就得到了侮辱性文件的出现概率
pos_abusive = np.sum(train_category) / train_doc_num
# 单词出现的次数
p0num = np.ones(words_num)
p1num = np.ones(words_num)
print(p1num)
p0num_all = 2.0
p1num_all = 2.0
for i in range(train_doc_num):
# 遍历所有的文件,如果是侮辱性文件,就计算此侮辱性文件中出现的侮辱性单词的个数
if train_category[i] == 1:
p1num += train_mat[i]
p1num_all += np.sum(train_mat[i])
else:
p0num += train_mat[i]
p0num_all += np.sum(train_mat[i])
p1vec = np.log(p1num / p1num_all)
p0vec = np.log(p0num / p0num_all)
return p0vec, p1vec, pos_abusive
vec2classify: 待测数据[0,1,1,1,1…],即要分类的向量,p0vec: 类别0,即正常文档的, p1vec: 类别1,即侮辱性文档的,p_class1类别1,侮辱性文件的出现概率。使用算法: 乘法: P(C|F1F2...Fn) = P(F1F2...Fn|C)P(C)/P(F1F2...Fn),加法:P(F1|C)*P(F2|C)....P(Fn|C)P(C) -> log(P(F1|C))+log(P(F2|C))+....+log(P(Fn|C))+log(P(C)),使用 NumPy 数组来计算两个向量相乘的结果,这里的相乘是指对应元素相乘,即先将两个向量中的第一个元素相乘,然后将第2个元素相乘,以此类推。我的理解是: 这里的 vec2Classify * p1Vec 的意思就是将每个词与其对应的概率相关联起来,可以理解为 1.单词在词汇表中的条件下,文件是good 类别的概率 也可以理解为 2.在整个空间下,文件既在词汇表中又是good类别的概率。
def classify_naive_bayes(vec2classify, p0vec, p1vec, p_class1):
p1 = np.sum(vec2classify * p1vec) + np.log(p_class1)
p0 = np.sum(vec2classify * p0vec) + np.log(1 - p_class1)
if p1 > p0:
return 1
else:
return 0
5、测试算法
输入测试文件的对应词表,可以判断这个文件是友好的还是不友好的。例如我输入两个文件一部分词表,通过算法可以判断该邮件是友好还是非友好文件。其中词表['一番', '卑劣', '某人', '冷静', '以为', '真的', '不能', '有着', '这件', '清华', '心情 。', '一起 。', '解释',]是从友好文件中截取的,['邮箱', '地税', '查证', '树立', '较多现', '广州', '我司', '大小', '如贵司', '额度', '核心思想', '电脑', '真票 !', '每月', '洽商']是从非友好文件中截取的,最后算法预测的结果也是正确的。
def testing_naive_bayes():
# 1. 加载数据集
list_post, list_classes = load_data_set()
# 2. 创建单词集合
vocab_list = create_vocab_list(list_post)
# 3. 计算单词是否出现并创建数据矩阵
train_mat = []
for post_in in list_post:
train_mat.append(
# 返回m*len(vocab_list)的矩阵, 记录的都是0,1信息
set_of_words2vec(vocab_list, post_in)
)
# 4. 训练数据
p0v, p1v, p_abusive = train_naive_bayes(np.array(train_mat), np.array(list_classes))
# 5. 测试数据
test_one = ['一番', '卑劣', '某人', '冷静', '以为', '真的', '不能', '有着', '这件', '清华', '心情 。', '一起 。', '解释',]
print(test_one)
test_one_doc = np.array(set_of_words2vec(vocab_list, test_one))
print('这个邮件的类别是: {}'.format(classify_naive_bayes(test_one_doc, p0v, p1v, p_abusive)))
test_two = ['邮箱', '地税', '查证', '树立', '较多现', '广州', '我司', '大小', '如贵司', '额度', '核心思想', '电脑', '真票 !', '每月', '洽商']
print(test_two)
test_two_doc = np.array(set_of_words2vec(vocab_list, test_two))
print('这个邮件的类别是: {}'.format(classify_naive_bayes(test_two_doc, p0v, p1v, p_abusive)))

利用朴素贝叶斯进行垃圾邮件过滤
1、导入数据集
数据集中友好邮件和不友好邮件大概都是8500份。
2、垃圾邮件预测
垃圾邮件预测算法主要用到利用朴素贝叶斯进行文档分类中的贝叶斯分类器,通过分类器返回判断类型与实际类型比较,最终可以计算出错误比例。我这里友好文件和不友好文件都有1000份,对这些邮件处理返回概率之后,再从总共份文件中随机抽取100份进行预测,最后输出预测的结果。
def spam_test():
"""
对贝叶斯垃圾邮件分类器进行自动化处理。
:return: nothing
"""
doc_list = []
class_list = []
full_text = []
for i in range(1, 51):
try:
words = cut_sentences(open('TrainingSet/Ham/{}.txt'.format(i)).read())
except:
words = cut_sentences(open('TrainingSet/Ham/{}.txt'.format(i), encoding='Windows 1252').read())
doc_list.append(words)
full_text.extend(words)
class_list.append(1)
try:
# 添加非垃圾邮件
words = cut_sentences(open('TrainingSet/Ham/{}.txt'.format(i)).read())
except:
words = cut_sentences(open('TrainingSet/Ham/{}.txt'.format(i), encoding='Windows 1252').read())
doc_list.append(words)
full_text.extend(words)
class_list.append(0)
# 创建词汇表
vocab_list = create_vocab_list(doc_list)
import random
test_set = [int(num) for num in random.sample(range(100), 50)]
training_set = list(set(range(100)) - set(test_set))
training_mat = []
training_class = []
for doc_index in training_set:
training_mat.append(set_of_words2vec(vocab_list, doc_list[doc_index]))
training_class.append(class_list[doc_index])
p0v, p1v, p_spam = train_naive_bayes(
np.array(training_mat),
np.array(training_class)
)
# 开始测试
error_count = 0
for doc_index in test_set:
word_vec = set_of_words2vec(vocab_list, doc_list[doc_index])
if classify_naive_bayes(
np.array(word_vec),
p0v,
p1v,
p_spam
) != class_list[doc_index]:
error_count += 1
print('正确率为 {}'.format(
1 - (error_count / len(test_set))
))
总结
算法对大量的数据集不太友好,最开始我找了上万条的邮件作为数据集,最后运行出来的结果特别差错误率能达到0.9。最后不得不减少数据集,分别用500条友好和不友好的文件,一共抽取100条测试正确率,最后结果正确率只有0.18。

继续减小数据集,最后分别用50条友好和不友好的文件,一共抽取20条测试正确率,正确率只有0.28。应该是我的数据集里面每一封邮件内容过多,中文词组之间没有太大联系造成的。

朴素贝叶斯算法优点:
- 朴素贝叶斯模型有稳定的分类效率。
- 对小规模的数据表现很好,能处理多分类任务,适合增量式训练,尤其是数据量超出内存时,可以一批批的去增量训练。
- 对缺失数据不太敏感,算法也比较简单,常用于文本分类。
缺点:
- 理论上,朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为朴素贝叶斯模型给定输出类别的情况下,假设属性之间相互独立,这个假设在实际应用中往往是不成立的,在属性个数比较多或者属性之间相关性较大时,分类效果不好。而在属性相关性较小时,朴素贝叶斯性能最为良好。对于这一点,有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。
- 需要知道先验概率,且先验概率很多时候取决于假设,假设的模型可以有很多种,因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
- 对输入数据的表达形式很敏感。
代码地址:
链接:https://pan.baidu.com/s/1iXUTGRxISzWisOk_Wt6xXA?pwd=zrqx
提取码:zrqx