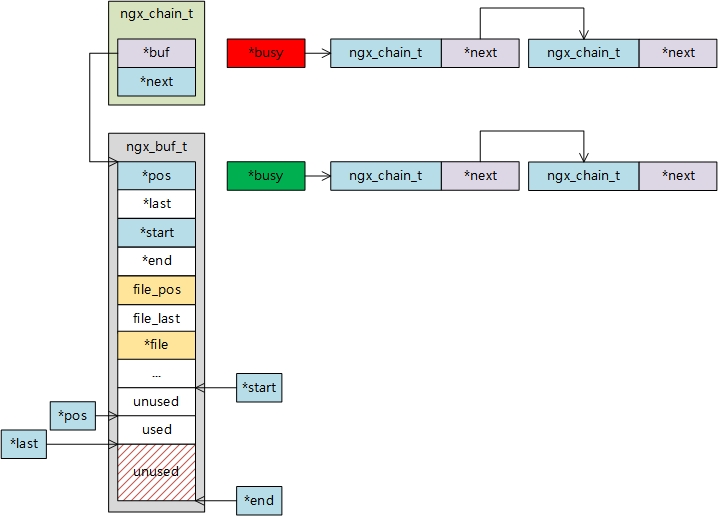
377. 组合总和 Ⅳ

给你一个由 不同 整数组成的数组 nums ，和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。
题目数据保证答案符合 32 位整数范围。

示例 1：
输入：nums = [1,2,3], target = 4
输出：7
解释：
所有可能的组合为：
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意，顺序不同的序列被视作不同的组合。

示例 2：
输入：nums = [9], target = 3
输出：0

---

求凑成总和的排列数，而不是把所有的排列都列出来。
如果本题要把排列都列出来的话，只能使用回溯算法爆搜。

求组合数：外层for循环：遍历物品，内层for遍历：背包容量。
求排列数：外层for遍历：背包容量，内层for遍历：遍历物品。

排列：元素相同 顺序不同的组合。
(1,5) 和 (5,1) 是同一个组合
(1,5) 和 (5,1) 是两个不同的排列

ps: 这道题属实很恶心！流程读不动，只能靠记…

---

Java代码1：完全背包

public int combinationSum4(int[] nums, int target) {
    int[] dp = new int[target + 1];
    dp[0] = 1;
    for(int j = 1; j <= target; ++j){ // 遍历背包
        for(int num : nums){          // 遍历物品
            if(j >= num){
                dp[j] = dp[j] + dp[j-num];
            }
        }
    }
    return dp[target];
}