Python数据结构与算法篇（二）-- 数组常见题型与解题技巧

数组和链表代表着计算机最基本的两种存储形式：顺序存储和链式存储，所以他俩可以算是最基本的数据结构。数组是一种基础数据结构，可以用来处理常见的排序和二分搜索问题，典型的处理技巧包括对双指针、滑动窗口等，数组是数据结构中的基本模块之一。因为字符串是由字符数组形成的，所以二者是相似的。

双指针⼜分为中间向两端扩散的双指针、两端向中间收缩的双指针、快慢指针。此外，数组还有前缀和和差分数组也属于必知必会的算法技巧。

1 常用技巧

1.1 滑动窗口/双指针

1. 定义

在计算机网络里经常用到滑动窗口协议（Sliding Window Protocol），该协议是 TCP协议的一种应用，用于网络数据传输时的流量控制，以避免拥塞的发生。该协议允许发送方在停止并等待确认前发送多个数据分组。由于发送方不必每发一个分组就停下来等待确认。因此该协议可以加速数据的传输，提高网络吞吐量。

滑动窗口算法其实和这个是一样的，只是用的地方场景不一样，可以根据需要调整窗口的大小，有时也可以是固定窗口大小。

滑动窗口使用双指针解决问题，所以一般也叫双指针算法，因为两个指针间形成一个窗口。双指针也并不局限在数组问题，像链表场景的 “快慢指针” 也属于双指针的场景，其快慢指针滑动过程中本身就会产生一个窗口，比如当窗口收缩到某种程度，可以得到一些结论。

什么情况适合用双指针呢？

需要输出或比较的结果在原数据结构中是连续排列的，特别是数组或链表问题；
每次窗口滑动时，只需观察窗口两端元素的变化，无论窗口多长，每次只操作两个头尾元素，当用到的窗口比较长时，可以显著减少操作次数；
窗口内元素的整体性比较强，窗口滑动可以只通过操作头尾两个位置的变化实现，但对比结果时往往要用到窗口中所有元素。

滑动窗口算法在一个特定大小的字符串或数组上进行操作，而不在整个字符串和数组上操作，这样就降低了问题的复杂度，从而也达到降低了循环的嵌套深度。其实这里就可以看出来滑动窗口主要应用在数组和字符串上。

2. 滑动窗口法的大体框架

在介绍滑动窗口的框架时候，大家先从字面理解下：

滑动：说明这个窗口是移动的，也就是移动是按照一定方向来的。
窗口：窗口大小并不是固定的，可以不断扩容直到满足一定的条件；也可以不断缩小，直到找到一个满足条件的最小窗口；当然也可以是固定大小。

为了便于理解，这里采用的是字符串来讲解。但是对于数组其实也是一样的。滑动窗口算法的思路是这样：

我们在字符串 S 中使用双指针中的左右指针技巧，初始化 left = right = 0，把索引闭区间 [left, right] 称为一个「窗口」。
我们先不断地增加 right 指针扩大窗口 [left, right]，直到窗口中的字符串符合要求（包含了 T 中的所有字符）。
此时，我们停止增加 right，转而不断增加 left 指针缩小窗口 [left, right]，直到窗口中的字符串不再符合要求（不包含 T 中的所有字符了）。同时，每次增加 left，我们都要更新一轮结果。
重复第 2 和第 3 步，直到 right 到达字符串 S 的尽头。

这个思路其实也不难，第 2 步相当于在寻找一个「可行解」，然后第 3 步在优化这个「可行解」，最终找到最优解。左右指针轮流前进，窗口大小增增减减，窗口不断向右滑动。

1.2 前缀和与差分数组

前缀和是指某序列的前 n 项和，可以把它理解为数学上的数列的前 n 项和，差分数组是与前缀和数组所对应的一种逆操作，类似于求导和积分，也就是说，对差分数组求前缀和，可以得到原数组，同样的，对前缀和数组求差分，也可以得到原数组。合理的使用前缀和与差分，可以将某些复杂的问题简单化。

1. 前缀和

假设有一个序列 A，前缀和为 S。根据概念很容易知到公式

$S[i]=\displaystyle \sum_{j=1}^iA[j]$

如何求区间 $[l, r]$ 的和呢？

$s u m [l, r] = s [r] - s [l - 1]$

2. 差分数组

设原数组为 A[i],差分数组为 diff[i]，则：

$diff[i]=\begin{cases} A[i]&i=1\\ A[i]-A[i-1]&i\geq2 \end{cases}$

差分数组的性质是：

如果对区间 $[l, r]$ 进行修改，只需修改 $d i ff [l], d i ff [r + 1]$ （diff[l]加上修改值，diff[r+1] 减去修改值）
$A[i]=\displaystyle \sum_{j=1}^{i}B[j]$ （通过 $B [i] = A [i] - A [i - 1]$ 证明）
$S[x]=\displaystyle \sum_{i=1}^{x}A[i]=\displaystyle \sum_{i=1}^{x} \displaystyle \sum_{j=1}^{i}diff[j]=\displaystyle \sum _{i=1}^{x}(x-i+1)*diff[i]$ $

当我们希望对原数组的某一个区间 [i, j] 施加一个增量 inc 时，差分数组d对应的变化是：d[i] 增加 inc，d[j+1] 减少 inc，并且这种操作是可以叠加的。

下面举个例子：

差分数组是一个辅助数组，从侧面来表示给定某一数组的变化，一般用来对数组进行区间修改的操作。

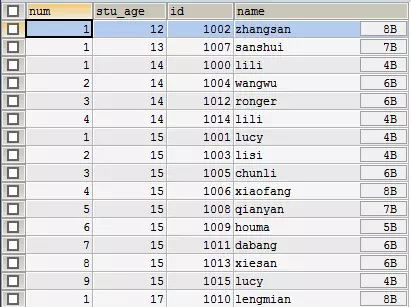
还是上面那个表里的例子，我们需要进行以下操作：

将区间[1，4]的数值全部加上3
将区间[3，5]的数值全部减去5

很简单对吧，你可以进行枚举。但是如果给你的数据量是 $1\times e^5$ ，操作量 $1\times e^5$ ，限时1000ms你暴力枚举能莽的过去吗？慢到你怀疑人生直接。这时我们就需要使用到差分数组了。

其实当你将原始数组中元素同时加上或者减掉某个数，那么他们的差分数组其实是不会变化的。

利用这个思想，咱们将区间缩小，缩小的例子中的区间 [1,4] 吧这是你会发现只有 d[1] 和 d[5] 发生了变化，而 d[2], d[3], d[4]却保持着原样，

进行下一个操作，

这时我们就会发现这样一个规律，当对一个区间进行增减某个值的时候，他的差分数组对应的区间左端点的值会同步变化，而他的右端点的后一个值则会相反地变化，其实这个很好理解。

本部分参考自：差分详解+例题

也就是说，当我们需要对原数组的不同区间施加不同的增量，我们只要按规则修改差分数组即可。所以，差分数组的主要适⽤场景是频繁对原始数组的某个区间的元素进⾏增减，但只能是区间元素同时增加或减少相同的数的情况才能用。

有 $n$ 个数， $m$ 个操作，每一次操作，将 $x\sim y$ 区间的所有数增加 $z$ ；最后有 $q$ 个询问，每一次询问求出 $x\sim y$ 的区间和。设原数组为 $A [i]$ 。其步骤为：

先求出差分数组 $B [i] = A [i] - A [i - 1]$
在根据 $m$ 个造作修改 $B [i]$
求修改后的 $A [i] = A [i - 1] + B [i]$
求前缀和 $S [i] = S [i - 1] + A [i]$
最后输出区间和 $s u m [x, y] = S [y] - S [x - 1]$

2 常见题型

2.1 删除数组元素

掌握数组删除元素的直接覆盖操作
双指针法

题库列表：

27. 移除元素（快慢指针）

26. 删除有序数组中的重复项（快慢指针）

80. 删除有序数组中的重复项 II
75. 颜色分类（双指针，三色旗，小米笔试）

27. 移除元素

题目描述：给你一个数组 nums 和一个值 val，你需要原地移除所有数值等于 val 的元素，并返回移除后数组的新长度。不要使用额外的数组空间，你必须仅使用 $O (1)$ 额外空间并原地修改输入数组。元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

class Solution:
    def removeElement(self, nums: List[int], val: int) -> int:
        '''拷贝覆盖'''
        ans = 0
        for num in nums:
            if num!= val:
                nums[ans] = num
                ans += 1
        return ans

26. 删除有序数组中的重复项

题目描述：给你一个升序排列的数组 nums ，请你原地删除重复出现的元素，使每个元素只出现一次，返回删除后数组的新长度。元素的相对顺序应该保持一致。

class Solution:
    def removeDuplicates(self, nums: List[int]) -> int:
        slow, fast = 0, 1
        while fast < len(nums):
            if nums[fast] != nums[slow]:
                slow += 1
                nums[slow] = nums[fast]
            fast += 1
        
        return slow + 1

80. 删除有序数组中的重复项 II

题目描述：给你一个有序数组 nums ，请你原地删除重复出现的元素，使得出现次数超过两次的元素只出现两次，返回删除后数组的新长度。不要使用额外的数组空间，你必须在原地修改输入数组并在使用 $O (1)$ 额外空间的条件下完成。

class Solution:
    def removeDuplicates(self, nums: List[int]) -> int:
        slow, fast = 1, 2
        while fast < len(nums):
            if nums[fast] != nums[slow-1]:
                slow += 1
                nums[slow] = nums[fast]
            fast += 1
        return  slow + 1

通用解法：

为了让解法更具有一般性，我们将原问题的 「最多保留 1 位」修改为「最多保留 k 位。

对于此类问题，我们应该进行如下考虑：

由于是保留 k 个相同数字，对于前 k 个数字，我们可以直接保留。

对于后面的任意数字，能够保留的前提是：与当前写入的位置前面的第 k 个元素进行比较，不相同则保留。

此时，初始化时指针 p 指向数组的起始位置（nums[k-1]），指针 q 指向指针 p 的后一个位置（nums[k]）。随着指针 q 不断向后移动，将指针 q 指向的元素与指 p 指向的元素进行比较：

如果nums[q] ≠ nums[p-k+1]，那么nums[p + 1] = nums[q]；
如果nums[q] = nums[p]，那么指针q继续向后查找；

75. 颜色分类

题目描述：给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。

1. 单指针

class Solution:
    def sortColors(self, nums: List[int]) -> None:
        i = 0
        length = len(nums)
        for j in range(length):
            if nums[j] == 0:
                nums[i], nums[j] = nums[j], nums[i]
                i += 1
        for k in range(i, length):
            if nums[k] == 1:
                nums[k], nums[i] = nums[i], nums[k]
                i += 1

2. 双指针

class Solution:
    def sortColors(self, nums: List[int]) -> None:
        # 定义三个变量，p0 表示数组最左边0的区域，p1是数组最右边2的区域
        i, p0, p1 = 0, 0 , len(nums)-1
        while i <= p1:
            # 如果当前指向的是 0，就把这个元素交换到数组左边
			# 也就是跟 p0 指针交换，之后cur，p0 就往前一动一位
            if nums[i] == 0:
                nums[i], nums[p0] = nums[p0], nums[i]
                p0 += 1
                i += 1
            # 如果当前指向的是2，就把这个元素交换到数组右边
			# 也就是跟p2指针交换，注意此时cur指针就不用移动了
			# 因为右边的一片区域都是2，只要把元素交换过去就可以了，cur不用移动
            elif nums[i] == 2:
                nums[i], nums[p1] = nums[p1], nums[i]
                p1 -= 1
            # 如果是1的话，就不用交换	
            else:
                i += 1

2.2 双指针技巧

题库列表：

88. 合并两个有序数组：如何将数组所有元素整体后移，防止数组覆盖？
167. 两数之和 II - 输入有序数组（有序数列的首尾双指针）
125. 验证回文串
345. 反转字符串中的元音字母
11. 盛最多水的容器：经典题目
209. 长度最小的子数组：滑动窗口
56. 合并区间：数组类操作

88. 合并两个有序数组

题目描述：给你两个按非递减顺序排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。请你合并 nums2 到 nums1 中，使合并后的数组同样按非递减顺序排列

逆向双指针

class Solution:
    def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
        """
        nums1[m:] = nums2               # 直接合并后排序
        nums1.sort()           
        """
        p0, p1, p2 = m-1, n-1, m+n-1
        while p0 >= 0 or p1 >= 0:
            if p0 == -1:
                nums1[p2] = nums2[p1]
                p1 -= 1
            elif p1 == -1:
                nums1[p2] = nums1[p0]
                p0 -= 1
            elif nums1[p0] > nums2[p1]:
                nums1[p2] = nums1[p0]
                p0 -= 1
            else:
                nums1[p2] = nums2[p1]
                p1 -= 1
            p2 -= 1

167. 两数之和 II - 输入有序数组

题目描述：给你一个下标从 1 开始的整数数组 numbers ，该数组已按非递减顺序排列，请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ，则 1 <= index1 < index2 <= numbers.length 。以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。

class Solution:
    def twoSum(self, numbers: List[int], target: int) -> List[int]:
        head, tail = 0, len(numbers)-1
        while head < tail:
            two_sum = numbers[head] + numbers[tail]
            if two_sum == target:
                return [head+1, tail+1]
            elif two_sum > target:
                tail -= 1
            else:
                head += 1

125. 验证回文串

题目描述：如果在将所有大写字符转换为小写字符、并移除所有非字母数字字符之后，短语正着读和反着读都一样。则可以认为该短语是一个回文串。字母和数字都属于字母数字字符。

import re
class Solution:
    def isPalindrome(self, s: str) -> bool:
        '''
        # 思路一：正则表达式
        if not s:
            return True
        s = s.lower()
        pattern = re.compile(r'[^a-z0-9]')   # 正则表达式，把数字和字母都剔除掉
        new_str = pattern.sub('', s)
        return new_str == new_str[::-1]
        '''
        # 字符串预处理
        new_str = ''.join(ch.lower() for ch in s if ch.isalnum())
        return new_str == new_str[::-1]

这里使用了正则表达式移除所有非字母数字字符，然后判断新的字符串是否是回文，也可以使用双指针，直接一次遍历，遇到字母数字字符就进行判断。

345. 反转字符串中的元音字母

题目描述：给你一个字符串 s ，仅反转字符串中的所有元音字母，并返回结果字符串。元音字母包括 ‘a’、‘e’、‘i’、‘o’、‘u’，且可能以大小写两种形式出现不止一次。

class Solution:
    def reverseVowels(self, s: str) -> str:
        str_set = set("aeiouAEIOU")
        head, tail = 0, len(s) - 1
        str_list = list(s)
        while head < tail:
            if str_list[head] in str_set and str_list[tail] in str_set:
                str_list[head], str_list[tail] = str_list[tail], str_list[head]
                head += 1
                tail -= 1
            elif str_list[head] in str_set and str_list[tail] not in str_set:
                tail -= 1
            elif str_list[head] not in str_set and str_list[tail] in str_set:
                head += 1
            else:
                head += 1
                tail -= 1
        return ''.join(str_list)

11. 盛最多水的容器

题目描述：给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。

class Solution:
    def maxArea(self, height: List[int]) -> int:
        # 双指针，移动小的那一边
        head, tail = 0, len(height)-1
        res = 0
        while head < tail:
            if height[head] < height[tail]:
                res = max(res, height[head]*(tail-head))
                head += 1
            else:
                res = max(res, height[tail]*(tail-head))
                tail -= 1
        return res

209. 长度最小的子数组

题目描述：给定一个含有 n 个正整数的数组和一个正整数 target。找出该数组中满足其和 ≥ target 的长度最小的连续子数组 $nums_l, nums_{l+1}, ..., nums_{r-1}, nums_r]$ ，并返回其长度。如果不存在符合条件的子数组，返回 0。

class Solution:
    def minSubArrayLen(self, target: int, nums: List[int]) -> int:
        '''
        我们把数组中的右指针右移，直到总和大于等于 target 为止，记录个数；
        然后左指针右移，直到队列中元素的和小于 target 为止，记录个数；
        重复，直到右指针到达队尾。
        '''
        if min(nums) > target or sum(nums) < target:
            return 0
        min_len = inf
        head, tail = 0, 0
        total = 0
        while tail < len(nums):     # 右指针滑动
            total += nums[tail]
            while total >= target:  # 固定右指针，滑动左指针，求最小子数组
                min_len = min(min_len, tail - head + 1)
                total -= nums[head]
                head += 1
            tail += 1

        return min_len

56. 合并区间

题目描述：以数组 intervals 表示若干个区间的集合，其中单个区间为 $in t er v a l s [i] = [s t a r t i, e n d i]$ 。请你合并所有重叠的区间，并返回一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间。

class Solution:
    def merge(self, intervals: List[List[int]]) -> List[List[int]]:
        result= []
        intervals.sort(key=lambda x:x[0])
        for interval in intervals:
            # 如果列表为空，或者当前区间与上一区间不重合，直接添加
            if not result or result[-1][1] < interval[0]:
                result.append(interval)
            else:
                # 否则的话，我们就可以与上一区间进行合并
                result[-1][1] = max(result[-1][1], interval[1])
        return result

2.3 前缀和与差分数组

题库列表：

303. 区域和检索 - 数组不可变：一维前缀和
304. 二维区域和检索 - 矩阵不可变：二维前缀和
370. 区间加法：差分数组
1109. 航班预订统计：差分数组
1094. 拼车：差分数组

303. 区域和检索 - 数组不可变

题目描述：

一维前缀和

class NumArray:

    def __init__(self, nums: List[int]):
        self.nums_array = [0]            # 便于计算累加和
        for i in range(len(nums)):
            self.nums_array.append(self.nums_array[i] + nums[i])  # 计算nums累加和

    def sumRange(self, left: int, right: int) -> int:
        return self.nums_array[right+1] - self.nums_array[left]

304. 二维区域和检索 - 矩阵不可变

题目描述：

二维前缀和

class NumMatrix:

    def __init__(self, matrix: List[List[int]]):
        m, n = len(matrix), len(matrix[0])                  # 矩阵的行和列
        self.pre_sum = [[0]*(n+1) for _ in range(m+1)]      # 构造一维前缀和矩阵
        for i in range(m):
            for j in range(n):
                self.pre_sum[i+1][j+1] = self.pre_sum[i+1][j] + self.pre_sum[i][j+1] - self.pre_sum[i][j] + matrix[i][j]

    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
        return (self.pre_sum[row2+1][col2+1] - self.pre_sum[row1][col2+1] - self.pre_sum[row2+1][col1] + self.pre_sum[row1][col1])

370. 区间加法

题目描述：假设你有一个长度为n的数组，初始情况下所有的数字均为0，你将会被给出k个更新的操作。其中，每个操作会被表示为一个三元组: [startIndex, endIndex, inc]，你需要将子数组 A[startIndex, endIndex]（包括startlndex和endIndex）增加 inc。
请你返回 k 次操作后的数组。

class Solution:
    def getModifiedArray(self, length: int, updates: List[List[int]]) -> List[int]:
        diff = [0] * (length+1)  # 末尾多个0，防止越界
        
        for update in updates:
            start, end, inc = update[0], update[1], update[2]
            diff[start] += inc
            diff[end + 1] -= inc
        
        for i in range(1, length):
            diff[i] += diff[i - 1]            # 对差分数组求前缀和便可得到原数组
            
        return diff[:-1]

1109. 航班预订统计

题目描述：这里有 n 个航班，它们分别从 1 到 n 进行编号。有一份航班预订表 bookings ，表中第 $i$ 条预订记录 $bookings[i] = [first_i, last_i, seats_i]$ 意味着在从 $first_i$ 到 $last_i$ （包含 $first_i$ 和 $last_i$ ）的每个航班上预订了 $seats_i$ 个座位。请你返回一个长度为 n 的数组 answer，里面的元素是每个航班预定的座位总数。

class Solution:
    def corpFlightBookings(self, bookings: List[List[int]], n: int) -> List[int]:
        diff = [0] * (n+1)
        for booking in bookings:
            start, end, inc = booking[0], booking[1], booking[2]
            diff[start] += inc
            if end < n:             # 没在末尾添加0，要判断一下边界
                diff[end+1] -= inc
        for i in range(1, n+1):
            diff[i] += diff[i-1]
        return diff[1:]

1094. 拼车

题目描述：车上最初有 capacity 个空座位。车只能向一个方向行驶（也就是说，不允许掉头或改变方向），给定整数 capacity 和一个数组 trips , $trip[i] = [numPassengers_i, from_i, to_i]$ 表示第 $i$ 次旅行有 $numPassengers_i$ 乘客，接他们和放他们的位置分别是 $from_i$ 和 $to_i$ 。这些位置是从汽车的初始位置向东的公里数。当且仅当你可以在所有给定的行程中接送所有乘客时，返回 true，否则请返回 false。

class Solution:
    def carPooling(self, trips: List[List[int]], capacity: int) -> bool:
        diff = [0] * (1001)      					# 题目中最多有1001个车站
        max_station = 0          					# 找到车站数
        for trip in trips:
            inc, start, end = trip[0], trip[1], trip[2]
            diff[start] += inc
            diff[end] -= inc      					# 第end站乘客已经下车，这里就不用end+1
            max_station = max(max_station, end)
        for i in range(1, max_station+1): 			# 进行区间求和
            diff[i] += diff[i-1]
        if max(diff[:max_station]) > capacity:
            return False
        return True