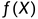题目描述
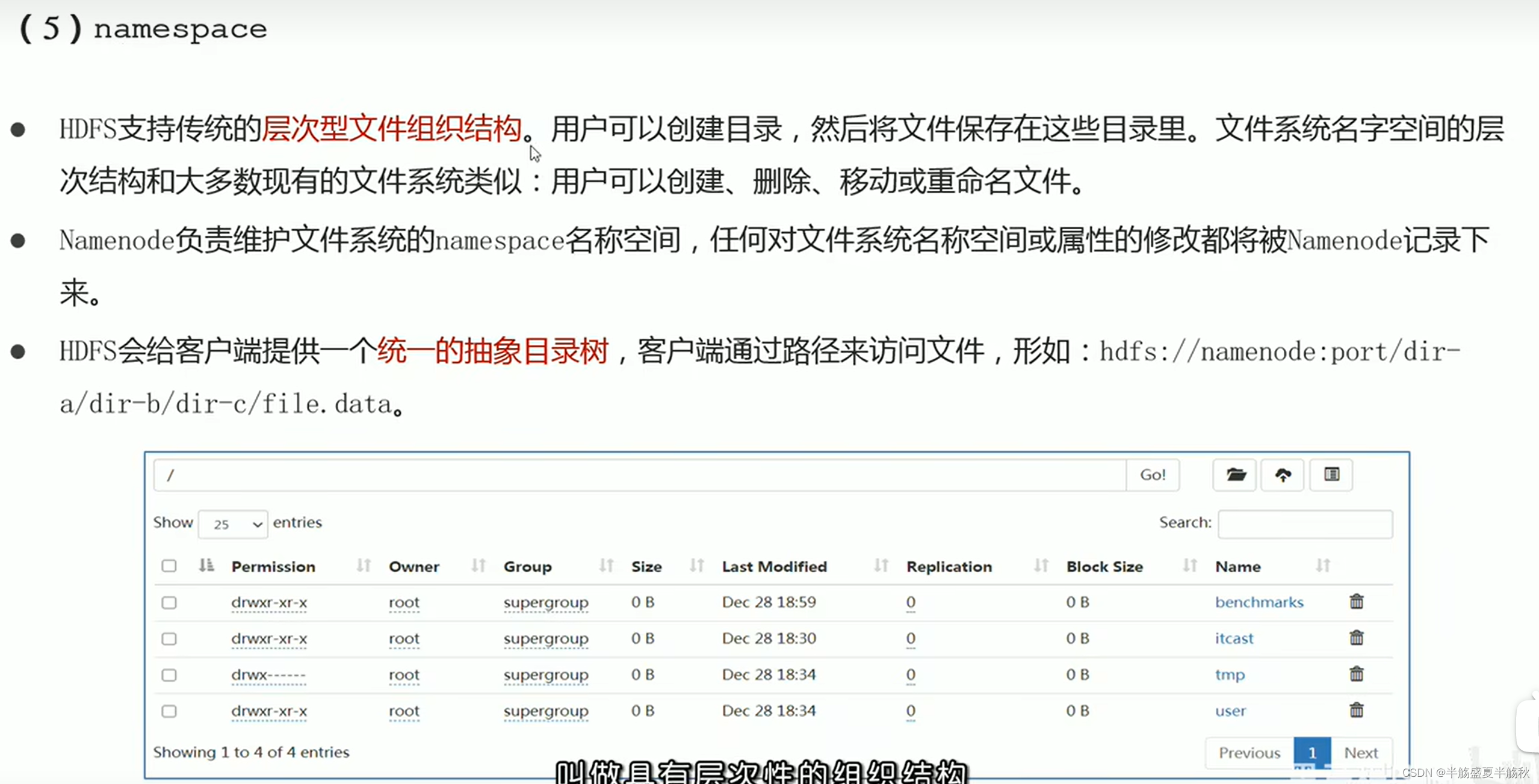
小明非常不喜欢数字 2，包括那些数位上包含数字 2 的数。如果一个数的数位不包含数字 2，小明将它称为洁净数。

请问在整数 1 至 n 中，洁净数有多少个？

输入描述
输入的第一行包含一个整数 n(1≤n≤10^6)。

输出描述
输出一行包含一个整数，表示答案。

输入输出样例
示例
输入

30
输出

18
运行限制
最大运行时间：1s
最大运行内存: 256M

所需变量

int shuwei;//代表没位数上是多少

int n;//代表终止条件的n

int sum = 0;//代表中共有多少个洁净数，初始化为0

int i;//循环变量

思路:我们首先要知道判断一个数的数位上是否有2，如果2我们就返回0，如果没有就返回一，具体做法就是首先把每位都分别取出来，然后对其进行判断是否是2，如果是2，直接就返回0，如果不是2，那我们接着判断直到全部不为2，或者有一个就终止判断条件，这样我们就跳出循环！

int solution(int a){
  int shuwei = 0;
  while(a>0){
    shuwei = a%10;
    if(shuwei == 2){
      return 0;
    }
    a = a/10;
  }
  return 1;
}

对于程序main函数我们首先要获取n，得到n之后我们就不断的将1到n中的数不断输入解决函数中，以此判断是否为洁净数，最后如果每次判断返回1那么我们总数就+1，最后得到总数sum输出出来就可以了！
该算法本人认为比较优，如果有更好的想法，欢迎q我！
代码如下（编译器是dev，语言是C语言）

#include <iostream>
using namespace std;
int solution(int a){
  int shuwei = 0;
  while(a>0){
    shuwei = a%10;
    if(shuwei == 2){
      return 0;
    }
    a = a/10;
  }
  return 1;
}
int main()
{
  int n;
  int i,sum = 0;
  cin>>n;
  for(i = 1;i<=n;i++){
    if(solution(i)){
      sum++;
    }
  }
  cout<<sum<<endl;
  return 0;
}