第一章 概论
统计学习，又称统计机器学习（机器学习），现在提到的 机器学习 往往指的就是 统计机器学习。
统计学习研究的对象是数据，其对数据的基本假设是同类数据存在一定的统计规律性，因此可以用概率统计方法处理他们：用随机变量描述数据中的特征，用概率分布描述数据的统计规律，然后基于数据构建概率统计模型从而对数据进行预测和分析。
统计学习假设数据是独立同分布（i.i.d.）
1.1 统计学习的分类
统计学习方法一般包括一下几种：
监督学习
监督学习假设输入随机变量X和输出随机变量Y遵循联合概率分布
。
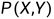监督学习的模型可以是概率模型：条件概率分布
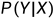，也可以是非概率模型：决策函数
。对具体的输入做预测，写作
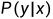或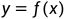
。通过学习（训练）得到一个模型为条件概率分布
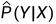或决策函数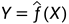
。
无监督学习
无监督学习的本质是学习数据中的统计规律或潜在结构。
假设
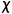是输入空间，
是隐式结构空间，无监督学习要学习的模型可表示为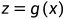
或条件概率分布
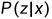或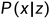
强化学习
半监督学习与主动学习
统计学习按照模型的种类，可分为：
概率模型和非概率模型 （二者区别不在于输入与输出映射关系，而在于模型内部结构）
概率模型：决策树、朴素贝叶斯、隐马尔可夫模型、条件随机场、概率潜在语义分析、潜在狄利克雷分配、高斯混合模型。代表是概率图模型（贝叶斯网络、马尔科夫随机场、条件随机场）
非概率模型：感知机、支持向量机、k近邻、AdaBoost、k均值、潜在语义分析、神经网络
线性模型和非线性模型
线性模型：感知机、线性支持向量机、k近邻、k均值、潜在语义分析
非线性模型：核函数支持向量机、AdaBoost、神经网络
参数化模型和非参数化模型
按照算法来分，可以分为：在线学习和批量学习
按照技巧来分，可以分为：贝叶斯学习和核方法
1.2 统计学习三要素
统计学习三要素：模型、策略、算法。
在监督学习中，模型就是所要学习的条件概率分布或决策函数。算法指学习模型的具体计算方法，可以利用已有的最优化算法，有时也需要开发独自的最优化算法。策略是按照什么样的准则从模型的假设空间
中选取最优模型。下面主要讲策略。
损失函数度量模型一次预测的好坏，风险函数度量平均意义下模型预测的好坏。
期望风险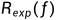
是模型关于联合分布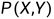的期望损失；经验风险
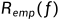是模型关于训练样本集的平均损失。根据大数定律，当样本容量N趋于无穷时，经验风险趋于期望风险。所以一个很自然地想法就是用经验风险估计期望风险。答案现实中样本往往是有限的，所以用经验风险估计期望风险往往不是很理想，要对经验风险进行一定矫正。
这就引出了监督学习两个基本策略：经验风险最小化 和 结构风险最小化。
经验风险最小化就是我们在监督学习训练模型的时候，最小化经验风险（训练集的平均损失）；结构风险最小化等价于正则化，就是再经验风险上加上表示模型复杂度的正则化项或罚项。
经验或结构风险函数就是最优化的目标函数。
// 泛函：函数的函数。
1.3 泛化能力
泛化误差：学习到的模型对未知数据预测的误差，即为泛化误差。事实上，泛化误差就是所学习到的模型的期望风险。
泛化误差上界：TODO
1.4 生成模型与判别模型
监督学习方法可以分为 生成方法 和 判别方法，学到的模型分别是 生成模型 和 判别模型。
生成模型：由数据学习联合概率分布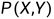，然后求出条件概率分布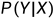作为预测的模型。即：
。
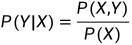这类方法之所以称为生成方法，是因为模型表示了给定输入X产生输出Y的生成关系。
典型的生成模型：朴素贝叶斯法、隐马尔可夫模型
判别模型：由数据直接学习决策函数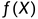
或条件概率分布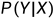作为预测的模型。
判别方法关心的是对给定的输入X，应该预测什么样的输出Y
典型的判别模型：k近邻法、感知机、逻辑斯蒂回归模型、最大熵模型、支持向量机、提升方法和条件随机场。
两类方法的优缺点：
生成方法：
生成方法可以还原出联合概率分布
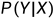，判别方法不能
生成方法的收敛速度更快
当存在隐变量时，仍可以用生成方法学习，但不能用判别方法
判别方法：
判别方法直接学习条件概率
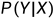或决策函数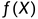，直接面对预测，往往学习准确率更高；
由于直接学习
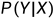或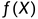，可以对数据进行各种程度上的抽象，定义特征并使用特征，因此可以简化学习问题。
