我们都知道，诸葛亮第一次北伐是最可能成功的，魏国没有防备，还策反了陇西，陇西有大量的马匹可以装备蜀国骑兵，可惜街亭一丢，那边就守不住了

当时我不在，只能作诗一首~

如果穿越过去，我将会向丞相献上一计，别说街亭，直接拿下长安，先看地图

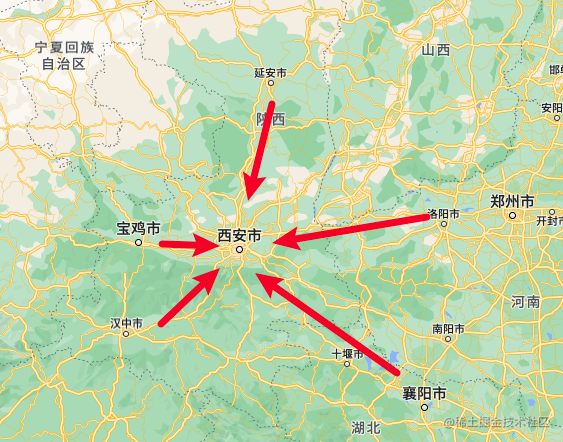
从延安，洛阳，策反魏国州长，让他们出兵。然后再结盟孙权，让他从久攻不下的合肥调来800精兵从襄阳进攻，让魏延从宝鸡出兵，自己率领大军从汉中进发

五路攻击，光围都能把长安围死

但是这个时候你可能会说：天方夜谭，且不说孙权，你怎么能确保洛阳和延安的兵听你的，而不是反贼？

这个呢，就需要我们今天要讲的问题，也称为【拜占庭将军问题】，多节点场景，没有中心化的协调，而且其中可能出现不可靠结点的情况下，如何保证大家行动的统一性？

我们先约定一些共识：

• 一个丞相发送指令，四个将军接收
• 所有人都可能是反贼
• 反贼回复的指令和丞相的相反

现在我们模拟一个场景，必须要五路进发才能够打下长安，其中有反贼。当主路——也就是诸葛亮的那一路发出“进攻”指令时，另外四路的将军会收到，同时会向其他三路求证，如果进攻指令数过半数，就会进攻。但是反贼会回复别的将军【撤退】指令

如果反贼过多，导致【撤退】指令过多，所有的将军都不会出动，丞相只能自己北伐了

• 那么此时忠反比多少才合适呢？

  关键在于，即使有反贼存在，只要忠臣数量足够多，就可以保证最终的决策是正确的。
  这是因为反贼无法破坏所有将军之间的通信，因此忠臣可以通过相互交流，确定反贼的存在并排除他们的虚假消息。最终的决策取决于忠臣的数量，通常情况下，当忠臣数量超过总将军数量的三分之二时，算法可以保证正确性。

• 那么为什么是三分之二呢？不是更多或者更少？

  假设发指令的是丞相，其他为将军，总数为n, 反贼数为m，

  其中每一个将军做判断的依据是接受到的指令取多数，

  每个将军自己在判断时，只会考虑别的将军和丞相的指令，排除自己，所以此时有n - 1个指令，那么会出现 m 个假指令和n - m - 1 个真指令

  只要保证 n - m - 1 > m，也就是 n > 2m + 1即可

  这是基本情况，当n = 3, m = 1时，满足n > 2m + 1，但是忠臣只会收到一个真指令和一个假指令，无法判断丞相或者另一个将军谁是反贼，所以为了确保取

  n > 3m，也就是忠臣占2/3多数

下面是一个简单的Java代码示例，演示了如何解决这个问题。

假设有6个将军，其中两个是反贼。每个将军都有一个唯一的ID和一个决策（attack或retreat）。这些将军之间通过消息传递来达成共识。

import java.util.Arrays;
import java.util.Random;
​
public class ByzantineGenerals {
​
    private static final int NUM_GENERALS = 6;
​
    private static final int REPEAT = 5;
    static int traitor;
    static int traitor2;
    public static void main(String[] args) {
​
        String[] orders = new String[NUM_GENERALS]; // 命令集合
        for (int p = 0; p < REPEAT; p++) {
            traitor = new Random().nextInt(NUM_GENERALS - 1);
            traitor2 = new Random().nextInt(NUM_GENERALS);
            if (traitor == traitor2) traitor2 += 1;
            for (int i = 0; i < NUM_GENERALS; i++) {
                orders[i] = (i == traitor || i == traitor2) ? "retreat" : "attack";
            }
​
            System.out.println("orders" + Arrays.toString(orders));
            boolean finalDecision = computeFinalDecision(orders);
            System.out.println("Final decision: " + (finalDecision ? "attack" : "retreat"));
            System.out.println();
        }
    }
​
    private static boolean computeFinalDecision(String[] orders) {
        boolean[] decisions = new boolean[NUM_GENERALS];
        for (int i = 0; i < NUM_GENERALS; i++) {
            if (i == traitor || i == traitor2) {
                decisions[i] = (new Random().nextBoolean());
            } else {
                boolean[] receivedOrders = new boolean[NUM_GENERALS - 1];
                int index = 0;
                for (int j = 0; j < NUM_GENERALS; j++) {
                    if (j != i) {
                        receivedOrders[index++] = (orders[j].equals("attack")); // 每一位将军收集命令
                    }
                }
                decisions[i] = computeDecision(receivedOrders);
            }
        }
        return computeDecision(decisions);
    }
​
    private static boolean computeDecision(boolean[] decisions) {
        // Compute the majority decision
        int numTrue = 0;
        int numFalse = 0;
        for (boolean decision : decisions) {
            if (decision) {
                numTrue++;
            } else {
                numFalse++;
            }
        }
        return (numTrue > numFalse);
    }
​
}

在上面的示例代码中，我们模拟了一个有6个将军的场景，并随机指定两个将军为反贼。每个将军都有一个决策，攻击或撤退。如果将军是反贼，他将发送虚假的命令，否则，将军将发送他真正的命令。在每个将军之间进行消息传递后，每个将军都会收到其他将军发送的命令。如果将军是反贼，他可能会给每个将军发送不同的命令，而忠臣将发送相同的命令。最后，每个将军都会将他们收到的命令和自己的命令一起计算出一个最终的决策，并将它们合并成一个共同的决策。

在计算决策的过程中，我们使用了一个简单的投票算法。我们将每个将军的决策转换为一个布尔值（attack为true，retreat为false），然后计算出这些布尔值中出现次数最多的值。如果attack出现的次数比retreat多，则我们最终的决策为attack，否则为retreat。

输出之一如下

orders[retreat, retreat, attack, attack, attack, attack]
Final decision: attack
​
orders[attack, attack, retreat, retreat, attack, attack]
Final decision: attack
​
orders[attack, attack, attack, retreat, retreat, attack]
Final decision: attack
​
orders[attack, attack, retreat, attack, retreat, attack]
Final decision: attack
​
orders[retreat, attack, attack, attack, attack, retreat]
Final decision: attack

可以看到在6个将军2个反贼下是符合 n > 2m + 1的场景，所以大家都是进攻

在n = 3， m = 1时，n > 2m + 1需要替换为 n > 3m

保险起见取 n > 3m即可

在我看来，这个问题是对投票解决问题的有效性和科学性很有力的佐证，比如选举，即使人民中藏了很多间谍或者是愚昧的人，但是只要正常人占了2/3以上，就可以确保这一制度的稳定与务实。

同时，如果诸葛亮使用我的计策，五路取长安，那么完全可以兴复汉室，还于旧都。剩下的只需要解决这一计策上面的两朵小乌云即可

1. 如何防止孙权背刺
2. 如何策反魏国两个地方的军队