在古老的迈瑞城，巍然屹立着 n 块神石。长老们商议，选取 3 块神石围成一个神坛。因为神坛的能量强度与它的面积成反比，因此神坛的面积越小越好。特殊地，如果有两块神石坐标相同，或者三块神石共线，神坛的面积为 0.000。

长老们发现这个问题没有那么简单，于是委托你编程解决这个难题。

输入格式：

输入在第一行给出一个正整数 n（3 ≤ n ≤ 5000）。随后 n 行，每行有两个整数，分别表示神石的横坐标、纵坐标（−109≤ 横坐标、纵坐标 <109）。

输出格式：

在一行中输出神坛的最小面积，四舍五入保留 3 位小数。

输入样例：

8
3 4
2 4
1 1
4 1
0 3
3 0
1 3
4 2

输出样例：

0.500

样例解释

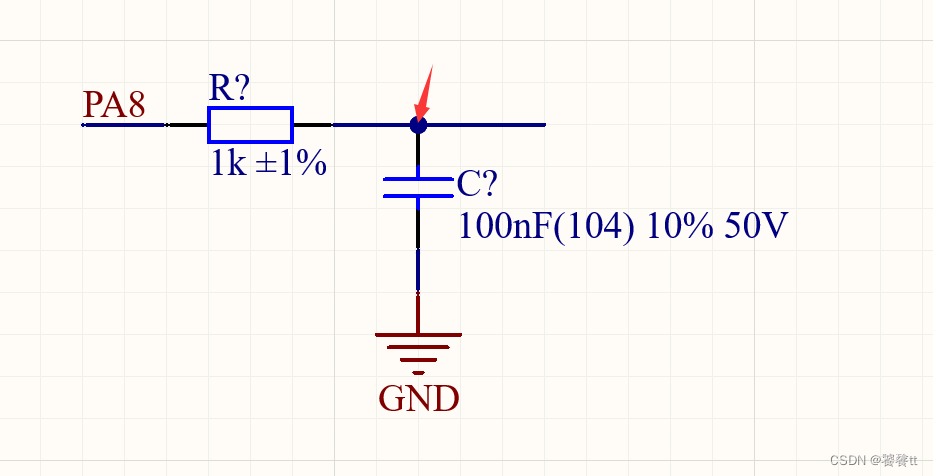
输出的数值等于图中红色或紫色框线的三角形的面积。

当你不会时：请记住最简单粗暴的方法（暴力版）

分析原因：是哪超时了呢，是因为什么超时的

得到结论：第三层for循环时，大部分时间都在进行无效的重复计算

大胆尝试：有没有什么办法可以让它不重复或者少重复呢

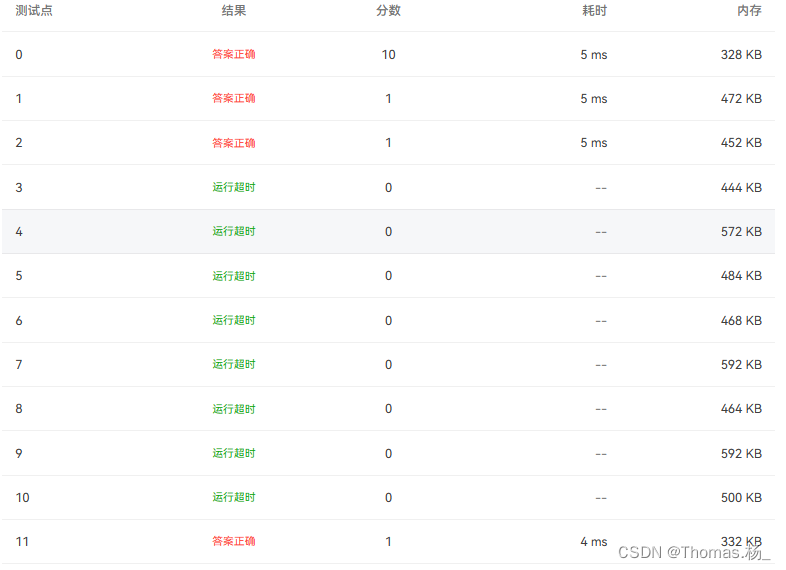
很不幸，还是如此，并没有得到跟多的分数，怎么办

--》时间不够，那就只能放弃了

--》还有时间，我能行，我可以的，我一定行

总结：三层循环嵌套肯定是不行了，我已经进全力优化了，到达极限了，不行啊。

极限分析：既然三层不行，那两层能不能实现呢，多写几个第二层的循环代替第三层行不行呢，试试？？？！！！

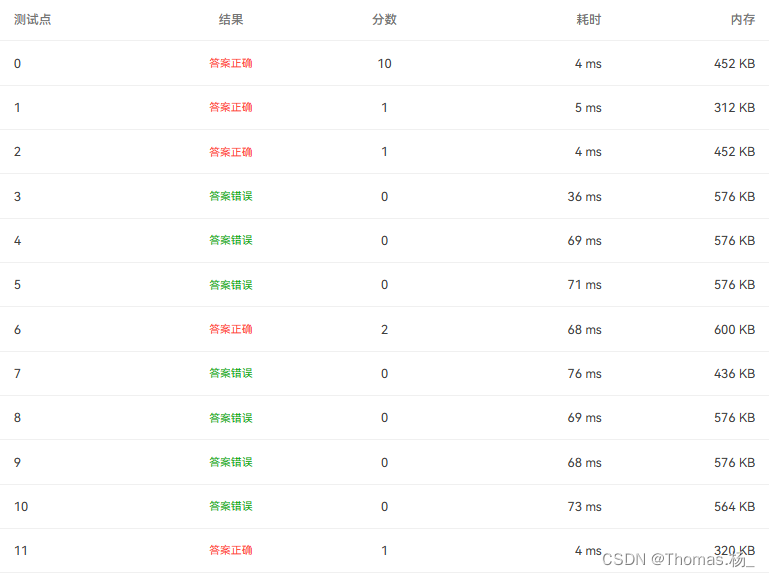
分析：很不错，又混了两分，目的达到了，超时问题已解决，接下来再试试能不能解决答案错误问题。为什么错了呢？？？？？？？？？？？？？？

结论：原来是因为 不相邻的两条边组成的三角形也可能比相邻的要小。

再想想办法，马上就要出来了。

//高数下第八章知识   向量的外积   =    |a||b|sin <a,b>

//        而三角形的面积公式    S   =1/2 |a||b|sin <a,b>

      

没注意横纵坐标范围（+10^9），MinArea给小了，而且由于有乘法，bouble把不够用

上天总是会眷顾努力的人，不是吗

相信自己，你可以的，你能行

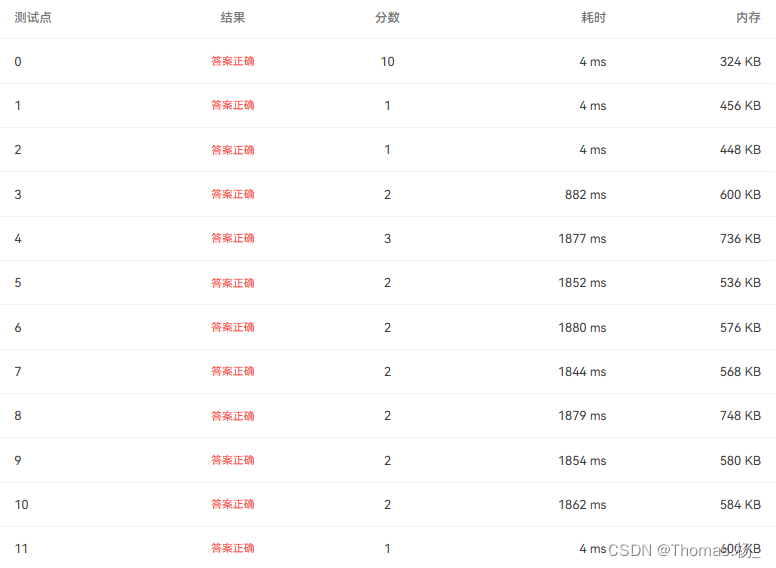
完整源代码：

#include <iostream>
#include<bits/stdc++.h>
#include <cmath>
using namespace std;

struct Point{
	long long x;//x坐标
	long long y;//y坐标
}p[5001];

bool cmp(Point a,Point b){//按顺时针排序
    return b.y*a.x>b.x*a.y;
	}

int main(){
	int n;
	scanf("%d",&n);
	for(int i=0; i<n; i++)
		scanf("%lld %lld",&p[i].x,&p[i].y);//scanf()的效率比cin高 
		
	long long MinArea=1e18;
	for(int i=0; i<n; i++){
		Point sides[n]; //每个点都能和其他n-1个点组成n-1条向量边 
		int k=0;
		for(int j=0; j<n; j++){
			if(i==j) continue;	
			sides[k++] = {p[j].x-p[i].x , p[j].y-p[i].y};//向量边  p[j]-p[i] 
		}
		sort(sides,sides+k,cmp);
		for(int j=1; j<k; j++){  //这是嵌套在第一层里面的第二循环，而不是嵌套在第二层里面的第三层循环	
			//三角形向量面积公式 S = 1/2 * | xA*yB - xB*yA |
			MinArea = min(MinArea,abs(sides[j].x*sides[j-1].y - sides[j-1].x*sides[j].y)); 
		}			
	} 
	
	printf("%.3f",MinArea/2.0);		
	return 0;		
}