之前我们介绍了中序线索二叉树的构造、遍历、寻找前趋和寻找后继;先序线索二叉树的构造、遍历、寻找后继。先序线索二叉树无法解决寻找前趋的任务,中序线索二叉树既可以寻找前趋结点也可以寻找后继结点。
今天我们再来看一下后序线索二叉树的构造:
首先是结构声明:
我们将左线索和右线索初始化为0。
/*
结构声明
*/
typedef struct node{
struct node* left;
int ltag = 0;
char val;
int rtag = 0;
struct node* right;
}TreeNode,*Tree; 后序构造线索二叉树的递归代码:
与中序构建线索二叉树的代码基本相同,把对当前结点的操作放到了遍历左右子树之后。
void PostThread(Tree& t, TreeNode* &pre){
//pre指针指向t的中序前驱,在主函数中预设为NULL
if(t != NULL){
PostThread(t->left, pre); //左子树线索化
PostThread(t->right, pre); //右子树线索化
if(t->left == NULL){ //建立当前结点的前驱线索
t->left = pre;
t->ltag = 1;
}
if(pre && pre->right == NULL){ //建立前驱结点pre的后继线索
pre->right = t;
pre->rtag = 1;
}
pre = t;
}
} 继续包装一下递归函数,与中序和先序不同的地方在于最后的pre指针指向根节点,所以不需要收尾。
/*
通过后序遍历建立后序线索二叉树
*/
void CreateThread(Tree& t){
TreeNode* pre = NULL; //前驱指针
if(t != NULL){
PostThread(t,pre);
}
} 后序线索二叉树访问前趋:
/*
返回结点p在线索二叉树中的后序序列下的前驱结点
如果有右孩子,则前驱是右孩子,如果没有右孩子,则前驱是左线索
*/
TreeNode* predecessor(TreeNode* p){
if(p->rtag == 0) return p->right;
return p->left;
} 后序线索二叉树不能很好的解决寻找后继。建立好后序线索二叉树之后,我们就可以根据线索和左右孩子指针以线性的时间来先序遍历后序线索二叉树了。
/*
后序线索二叉树不能很好的解决寻找后继。
这里给出一直求前驱得到的后序遍历的逆序列
*/
void PostOrder(TreeNode* t){
TreeNode*p = t;
for(p; p!= NULL; p = predecessor(p))
cout<< p->ltag <<" "<< p->val <<" "<< p->rtag <<" ";
}我们可以层次遍历一下,看看树打上标记后的样子。
/*
层次遍历
因为线索二叉树的叶子节点几乎没有了空指针,所以进队的条件应该做修改,用 ltag、rtag 来判断
*/
void levelOrderTraverse(Tree& t){
if(t == NULL) return;
queue<TreeNode*> q;
TreeNode* p;
q.push(t);
while(!q.empty()){
int width = q.size();
for(int i = 0;i < width;i ++){
p = q.front();
q.pop();
cout<<p->ltag<<" "<<p->val<<" "<<p->rtag<<" ";
if(p->ltag == 0) q.push(p->left);
if(p->rtag == 0) q.push(p->right);
}
cout<<endl;
}
} 完整代码:
#include<iostream>
#include<queue>
using namespace std;
/*
结构声明
*/
typedef struct node{
struct node* left;
int ltag = 0;
char val;
int rtag = 0;
struct node* right;
}TreeNode,*Tree;
void PostThread(Tree& t, TreeNode* &pre){
//pre指针指向t的中序前驱,在主函数中预设为NULL
if(t != NULL){
PostThread(t->left, pre); //左子树线索化
PostThread(t->right, pre); //右子树线索化
if(t->left == NULL){ //建立当前结点的前驱线索
t->left = pre;
t->ltag = 1;
}
if(pre && pre->right == NULL){ //建立前驱结点pre的后继线索
pre->right = t;
pre->rtag = 1;
}
pre = t;
}
}
/*
通过后序遍历建立后序线索二叉树
*/
void CreateThread(Tree& t){
TreeNode* pre = NULL; //前驱指针
if(t != NULL){
PostThread(t,pre);
}
}
/*
返回结点p在线索二叉树中的后序序列下的前驱结点
如果有右孩子,则前驱是右孩子,如果没有右孩子,则前驱是左线索
*/
TreeNode* predecessor(TreeNode* p){
if(p->rtag == 0) return p->right;
return p->left;
}
/*
后序线索二叉树不能很好的解决寻找后继。
这里给出一直求前驱得到的后序遍历的逆序列
*/
void PostOrder(TreeNode* t){
TreeNode*p = t;
for(p; p!= NULL; p = predecessor(p))
cout<< p->ltag <<" "<< p->val <<" "<< p->rtag <<" ";
}
/*
层次遍历
因为线索二叉树的叶子节点几乎没有了空指针,所以进队的条件应该做修改,用 ltag、rtag 来判断
*/
void levelOrderTraverse(Tree& t){
if(t == NULL) return;
queue<TreeNode*> q;
TreeNode* p;
q.push(t);
while(!q.empty()){
int width = q.size();
for(int i = 0;i < width;i ++){
p = q.front();
q.pop();
cout<<p->ltag<<" "<<p->val<<" "<<p->rtag<<" ";
if(p->ltag == 0) q.push(p->left);
if(p->rtag == 0) q.push(p->right);
}
cout<<endl;
}
}
/*
先序构造二叉树
*/
void CreateTree(Tree& t){
char x;
cin>>x;
if(x == '#') t = NULL;
else{
t = new TreeNode;
t->val = x;
CreateTree(t->left);
CreateTree(t->right);
}
}
int main(){
Tree t;
CreateTree(t);
TreeNode* parent;
/*
a b d # # e # # c f # # #
*/
CreateThread(t);
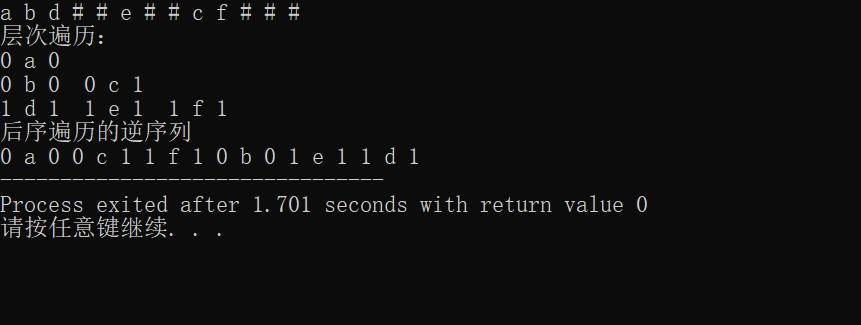
cout<<"层次遍历:"<<endl;
levelOrderTraverse(t);
cout<<"后序遍历的逆序列"<<endl;
PostOrder(t);
}程序运行结果: