Halo,这里是Ppeua。平时主要更新C语言,C++,数据结构算法......感兴趣就关注我吧!你定不会失望。
🌈个人主页:主页链接
🌈算法专栏:专栏链接
我会一直往里填充内容哒!
🌈LeetCode专栏:专栏链接
目前在刷初级算法的LeetBook 。若每日一题当中有力所能及的题目,也会当天做完发出
🌈代码仓库:Gitee链接
🌈点击关注=收获更多优质内容🌈
目录
DP:
题目:01背包问题
题解:
代码实现:
优化:
代码实现:
题目:完全背包
题解:
代码实现:
优化:
代码实现:
优化
代码实现:
完结撒花:
好**难啊,整抑郁了
DP:
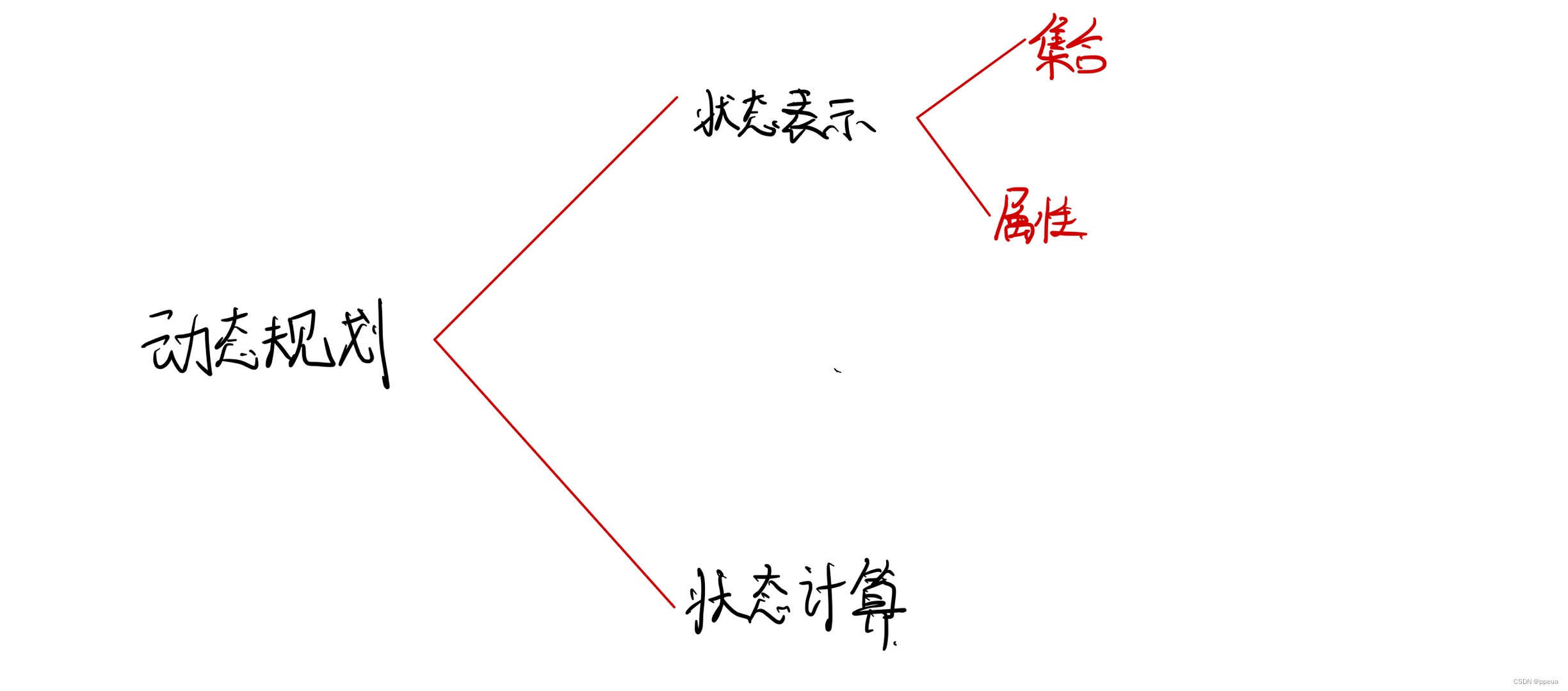
DP有这样的一个分析方法
题目:01背包问题
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i件物品的体积是 vi,价值是 wi
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。输入格式
第一行两个整数,N,V用空格隔开,分别表示物品数量和背包容积。
接下来有 N行,每行两个整数 vi,wi,用空格隔开,分别表示第 i件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000输入样例
4 5 1 2 2 4 3 4 4 5输出样例:
8
题解:
分析01背包问题的特点:有N件物品,背包容积是V,每件物品只能拿(0)或不拿(1),所以称为01背包问题.
将问题分析,当决定第i件拿与不拿的时候,表达式为:此时背包价值=max(背包没拿第i件物品的价值,拿了第i件物品的价值)
所以这里的状态表示的集合为:从前i件物品拿,且总体积不超过j
状态表示的属性为:最大值
状态计算为f[i][j],其中i为第几件物品,j为此时背包的容量
其中不选第i件物品总价值,就为前一个相同容量的背包中的价值
因为直接计算选第i件物品比较难计算,所以我们将选第i件物品的价值转换为,不选第i件物品的价值,并令其背包容积减去第i件物品的v再加上其价值w

所以我们的状态方程就为:f[i][j]=max(f[i-1],f[i-1][j-v]+w)
代码实现:
#include<iostream>
using namespace std;
int n, m;
const int N = 1010;
int v[N], w[N];
int f[N][N];
int solution1()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)cin >> v[i] >> w[i];
for (int i = 0; i <= m; i++)f[0][i] = 0;//一件物品都没选 0-m的容积下价值都为0
for (int i = 1; i <= n; i++)
{
for (int j = 0; j <= m; j++)
{
f[i][j] = f[i - 1][j];
if (j >= v[i])f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);//在拿i-1件物品,其容量为j-vi时放入物品的最大值
}
}
cout << f[n][m];
}
优化:
观察.f[i][j]的变换形式,每次计算只用到了上一层i,j,所以我们可以将i这一维给删了,变成这种形式
直接将[i]删了
int n, m;
const int N = 1010;
int v[N], w[N];
int f[N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)cin >> v[i] >> w[i];
for (int i = 0; i <= m; i++)f[i] = 0;//一件物品都没选 0-m的容积下价值都为0
for (int i = 1; i <= n; i++)
{
for (int j = v[i]; j<=m; j++)
{
f[j] = max(f[j], f[j - v[i]] + w[i]);//滚动数组优化,从后向前遍历,这样第一个的结果用到的是上一层的数据
}
}
cout << f[m];
}
但观察此时的状态方程.
f[j-v[i]]+w[i],用到的是这一层已经计算的数据(因为j是从小开始算的,也就是说从小的j开始就会把上一次计算的j给覆盖了,而后面要用到的是上面一层i-1的数据,而不是i)
所以我们为了避免这种情况,使用i-1的数据,我们从后往前遍历,这样每一次计算j时,用的就是i-1层的数据,与上文所述一致
代码实现:
int n, m;
const int N = 1010;
int v[N], w[N];
int f[N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)cin >> v[i] >> w[i];
for (int i = 0; i <= m; i++)f[i] = 0;//一件物品都没选 0-m的容积下价值都为0
for (int i = 1; i <= n; i++)
{
for (int j = m; j >= v[i]; j--)
{
f[j] = max(f[j], f[j - v[i]] + w[i]);//滚动数组优化,从后向前遍历,这样第一个的结果用到的是上一层的数据
}
}
cout << f[m];
}题目:完全背包
有 N种物品和一个容量是 V 的背包,每种物品都有无限件可用。
第 i种物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。输入格式
第一行两个整数N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有 N行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 种物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000输入样例
4 5 1 2 2 4 3 4 4 5输出样例:
10
题解:
完全背包问题是01背包问题的升级版.每件物品不再只能拿一件,而可以无限拿(在容量允许的情况下)
将问题分析,当决定第i件拿K件,表达式为:此时背包价值=max(背包没拿第i件物品的价值,拿了K*第i件物品的价值)
所以这里的状态表示的集合为:从前i件物品拿K件,且总体积不超过j
状态表示的属性为:最大值
状态计算为f[i][j],其中i为第几件物品,j为此时背包的容量
其中不选第i件物品总价值,就为前一个相同容量的背包中的价值
因为直接计算拿第i件k个比较难计算,所以我们将选第i件物品的价值转换为,不选第i件物品的价值,并令其背包容积减去第i件物品的K*v再加上其价值K*w

代码实现:
#include <algorithm>
#include<iostream>
using namespace std;
int n, m;
const int N = 1010;
int v[N], w[N];
int f[N][N];
int main()
{
for (int i = 1; i <= n; i++)cin >> v[i] >> w[i];
for (int i = 0; i <= m; i++)f[0][i] = 0;//一件物品都没选 0-m的容积下价值都为0
for(int i=1;i<=n;i++)
{
for(int j=0;j<=m;j++)
{
for(int k=0;k*v[i]<=j;k++)
{
f[i][j]=f[i-1][j];
if(j>=k*v[i])f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
}
}
}
cout<<f[n][m];
}这和01背包问题的朴素做法几乎一模一样,但这里的时间复杂度为n^3,所以我们得优化一下,不然就TLE了
优化:
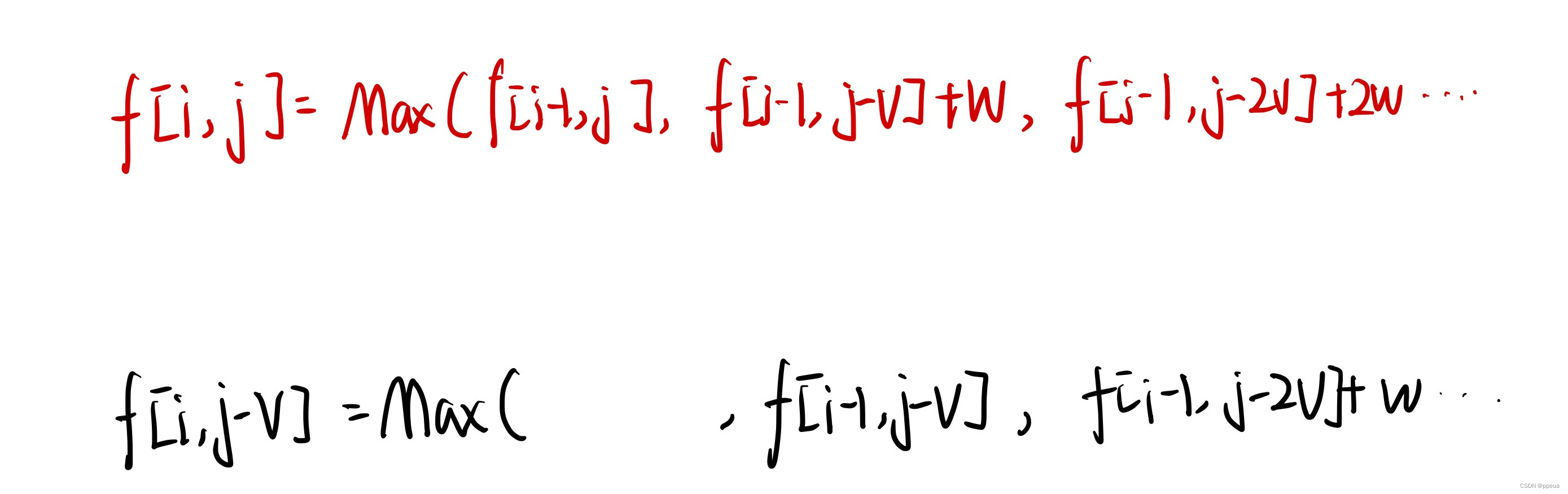
对于f[i,j-v]的含义是:将J>=K*V时,我们先将第i个物品放入背包,之后再去找当前容量下能放入的最大价值的东西,之后再加上w,这时候就可以不用考虑具体放几件了,
最后也就变成了f[i][j]=Max(f[i-1][j],f[i][j-v]+w)
代码实现:
#include <algorithm>
#include<iostream>
using namespace std;
int n, m;
const int N = 1010;
int v[N], w[N];
int f[N][N];
int main()
{
cin>>n>>m;
for (int i = 1; i <= n; i++)cin >> v[i] >> w[i];
for (int i = 0; i <= m; i++)f[0][i] = 0;//一件物品都没选 0-m的容积下价值都为0
for(int i=1;i<=n;i++)
{
for(int j=0;j<=m;j++)
{
f[i][j]=f[i-1][j];
if(j>=v[i])f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);//表示已经选入第i层
}
}
cout<<f[n][m];
}优化
因为还是N^2,观察这个表达式,和01背包问题很想,且也只用到了i-1层 所以可以用滚动数组优化,删掉一维即可,因为这里计算max的时候用的式i 所以不用进行从大到小的处理
代码实现:
#include <algorithm>
#include<iostream>
using namespace std;
int n, m;
const int N = 1010;
int v[N], w[N];
int f[N];
int main()
{
cin>>n>>m;
for (int i = 1; i <= n; i++)cin >> v[i] >> w[i];
for (int i = 0; i <= m; i++)f[i] = 0;//一件物品都没选 0-m的容积下价值都为0
for(int i=1;i<=n;i++)
{
for(int j=v[i];j<=m;j++)
{
f[j]=max(f[j],f[j-v[i]]+w[i]);//表示已经选入第i层
}
}
cout<<f[m];
}完结撒花:
🌈本篇博客的内容【动态规划 :背包问题(01背包,完全背包)】已经结束。
🌈若对你有些许帮助,可以点赞、关注、评论支持下博主,你的支持将是我前进路上最大的动力。
🌈若以上内容有任何问题,欢迎在评论区指出。若对以上内容有任何不解,都可私信评论询问。
🌈诸君,山顶见!






![基于gin-vue-admin[gin+gorm]手动实现crud(全)](https://img-blog.csdnimg.cn/8c43b1cc45084e648a4e85e060c58402.png)