前言
排序算法在面试中属于超高频的考点了,至少要学会如何手写各种排序算法,其中快速排序尤为重要
看完了本文以后,大家可以自己尝试着去手写一下这些排序算法啦,leetcode题号:75颜色分类
多努力点,活的精彩点~
冒泡排序
(1)基础概念
从后往前遍历,两两比较两个相邻元素的值,如果是逆序,就交换他们
(2)图解算法
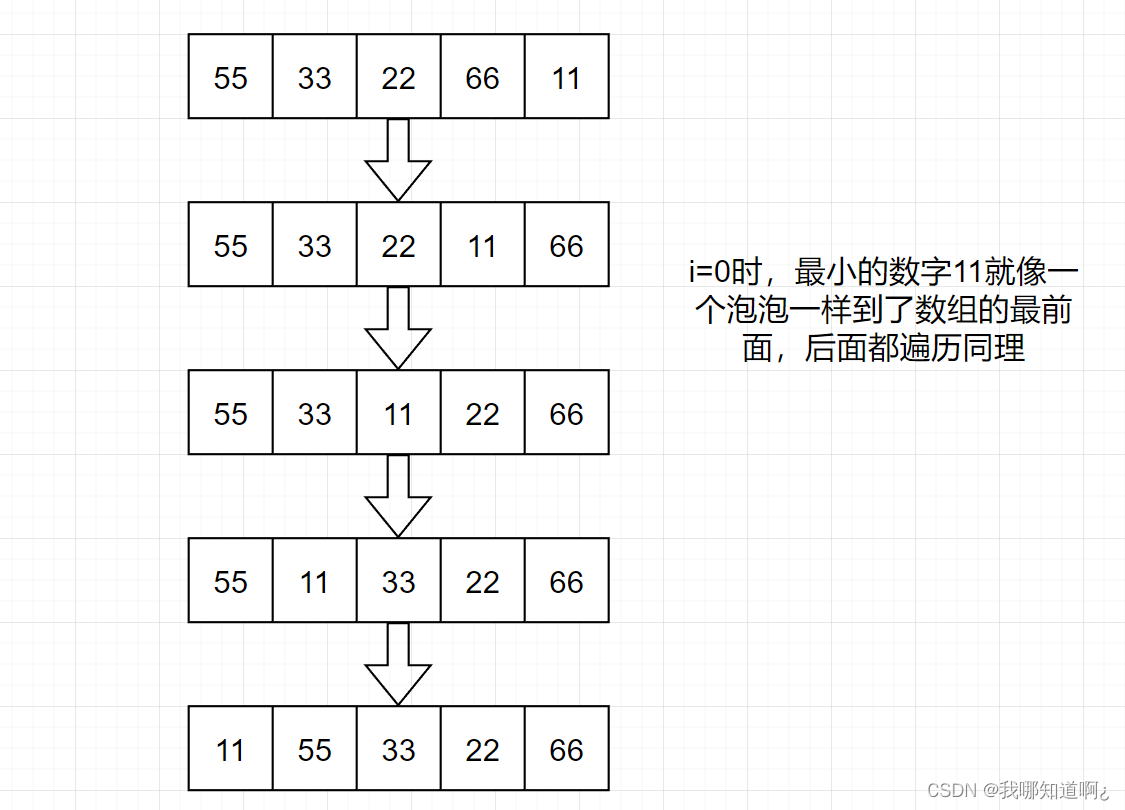
(3)代码实现
public void bubbleSort(int[] nums) {
for (int i = 0; i < nums.length; i++) {
//记录本次有没有交换
boolean flag = false;
for (int j = nums.length-1; j > i; j--) {
if (nums[j-1]>nums[j]){
int temp = nums[j];
nums[j]=nums[j-1];
nums[j-1]=temp;
flag=true;
}
}
//如果本次排序没有发生交换,说明数组已经是有序的了
if (!flag) return;
}
}
(4)算法效率分析
空间复杂度:O(1)
时间复杂度:
- O(n),数组本来就是有序的
- O(n²),数组是逆序的
插入排序
(1)基础概念
从数组下标为1的元素开始视为待排序的数字,将每一个待排序的数字插入到前面已经排好序的数组之中,直到全部插入完成
(2)图解算法
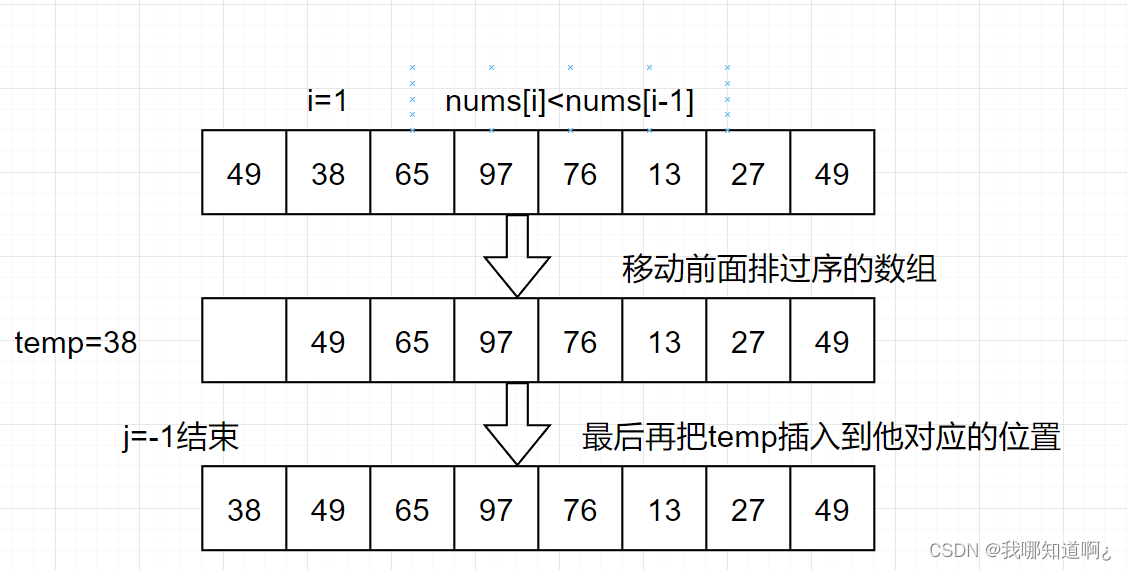
(3)代码实现
public void insertSorted(int[] nums) {
if (nums.length<=1) return;
//从i=1开始,将nums[i]插入到前面已经排好序的数组之中
for (int i = 1; i < nums.length; i++) {
//如果nums[i]小于前驱
if (nums[i]<nums[i-1]){
//暂存nums[i]
int temp = nums[i];
int j=i-1;
for (; j>=0&&nums[j]>temp ; j--) {
//所有大于temp的元素都向后挪一位
nums[j+1]=nums[j];
}
nums[j+1]=temp;
}
}
}
(4)算法效率分析
空间复杂度:O(1)
时间复杂度:
- O(n),数组本来就是有序的
- O(n²),数组是逆序的
快速排序
(1)基础概念
选取序列中的第一个数为基准,将待排序序列划分成两个部分,左边更小,右边更大。该元素的最终位置已确定。再分别递归对左右两个子表重复上述操作,直到每个部分内只有一个元素或空为止。
(2)图解算法

(3)代码实现
public void quickSort(int[] nums, int low, int high){
if (low<high){
int index = partition(nums,low,high);
//根据上一个基准数的位置,划分区间,继续排序
quickSort(nums,low,index-1);
quickSort(nums,index+1,high);
}
}
private int partition(int[] nums, int low, int high) {
//以第一个数作为基准
int pivot = nums[low];
while (low<high){
while (low<high&&nums[high]>=pivot) high--;
nums[low]=nums[high];//比基准数小的数都移动到左边
while (low<high&&nums[low]<=pivot) low++;
nums[high]=nums[low];//比基准数大的数都移动到右边
}
nums[low]=pivot;//基准数放到最终位置
return low;//返回基准数的位置
}
(4)算法效率分析
空间复杂度:每一次递归都需要定义固定的变量O(递归次数)
时间复杂度:
- 最好的情况,每次取的数正好是中位数,每一次都把区间划分成了两个数字个数相等的区间,O(nlogn),对于每一个区间,处理的时候都需要遍历所有元素,所以每一层的时间复杂度是n,由于每次都是中位数,一共logn层
- 最坏的情况,每次取的都是最大或者最小值,那么这样每次都只能将最小的元素放到区间最前面,那么就是n层了,同样的每一个区间在处理的时候都需要遍历,复杂度就来到了O(n²)
简单选择排序
(1)基础概念
每一趟都在待排序元素中选择一个最小的放到数组的首部
(2)图解算法
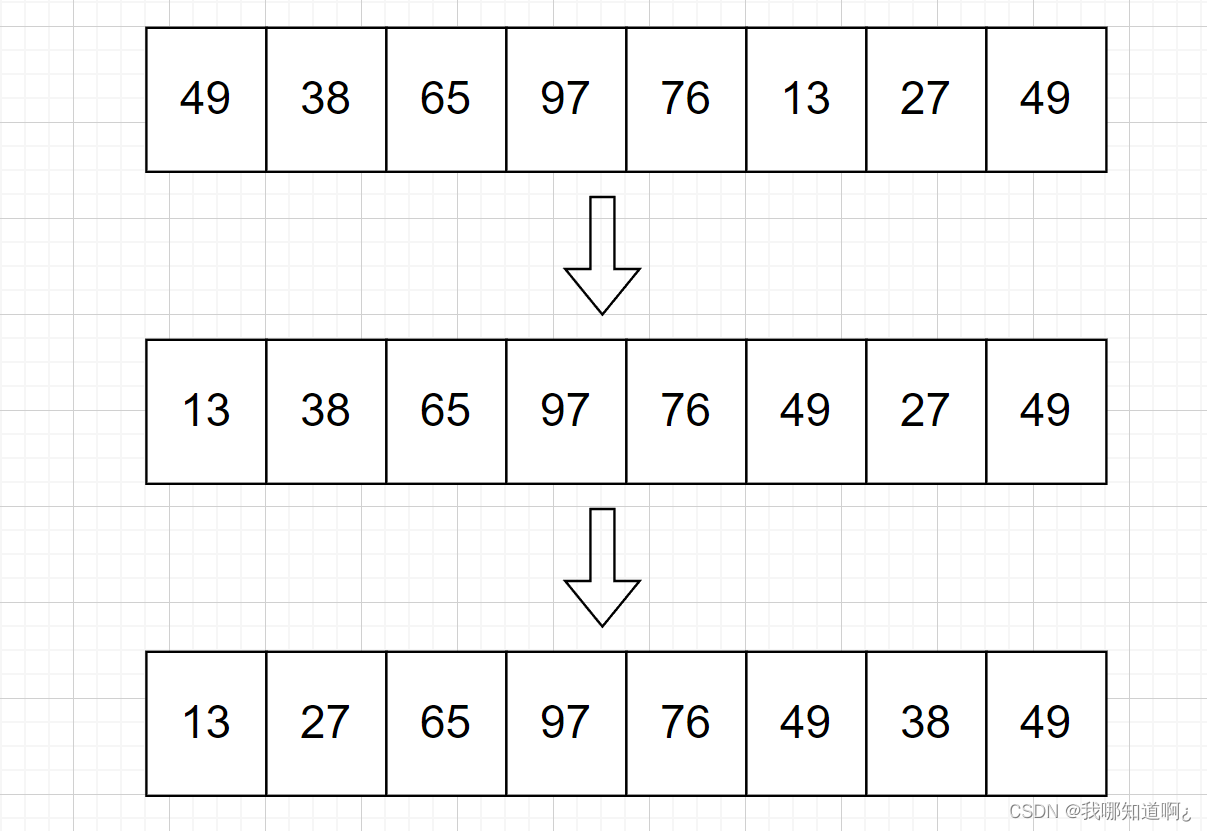
(3)代码实现
public void selectSort(int[] nums){
for (int i = 0; i < nums.length; i++) {
int min = i;
for (int j = i+1; j < nums.length; j++) {
if (nums[j]<nums[min]) min=j;
}
if (min!=i){
int temp = nums[min];
nums[min]=nums[i];
nums[i]=temp;
}
}
}
(4)算法效率分析
空间复杂度:O(1)
时间复杂度:O(n²)
希尔排序
(1)基础概念
先追求表中元素部分有序,再逐渐逼近全局有序,先将表分为若干个相距为d的子表,再对各个子表进行插入排序,缩小增量d,重复上述过程,直到d=1
(2)图解算法
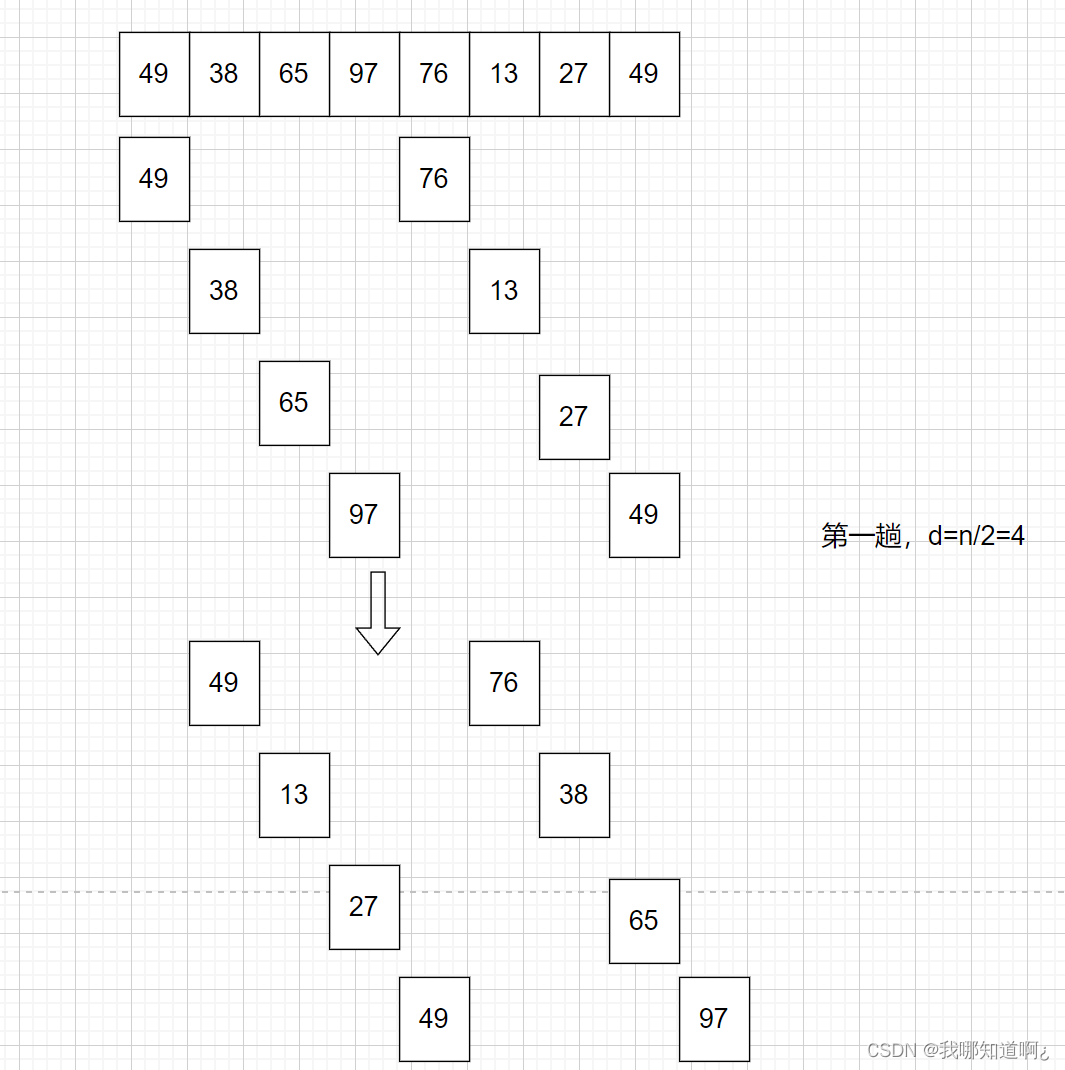
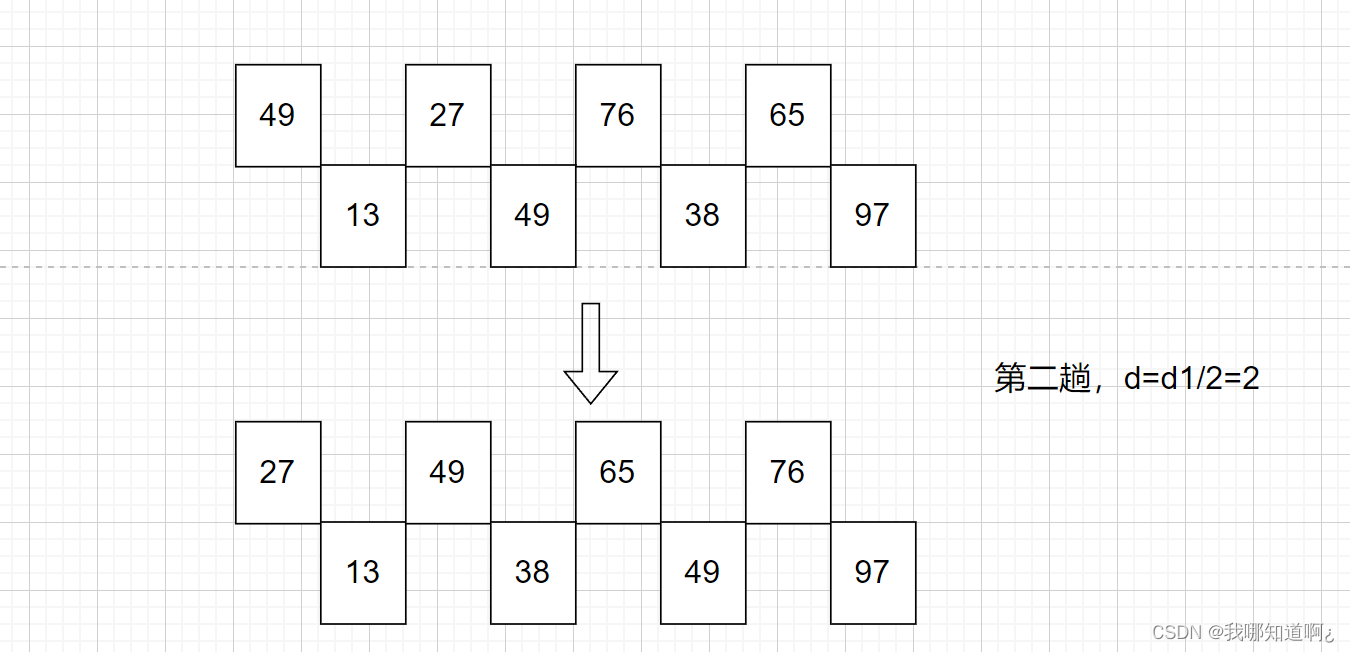
接下来,第三趟的时候,整个数组已经基本有序,再进行一次插入排序
(3)代码实现
public void shellColors(int[] nums) {
int temp = 0;
//定义步长,并逐步缩小,直到步长变为1
for (int d = nums.length/2; d >=1; d/=2) {
for (int i = d; i <nums.length; i++) {//循环处理每个子表
//当前元素位置不符合,需要将nums[i]插入有序增量子表
if (nums[i]<nums[i-d]){
//暂存nums[i]
temp = nums[i];
//以d为单位进行直接插入排序
int j = i-d;
for (; j >=0&&nums[j]>temp; j-=d) {
nums[j+d]=nums[j];
}
nums[j+d]=temp;
}
}
}
}
(4)算法效率分析
空间复杂度:1
时间复杂度:和增量d的选择有关,最坏的情况,d=1,那么就是插入排序O(n²)
堆排序
(1)基础概念
首先先明确两个概念
大根堆:根节点的值大于左右结点
小根堆:根节点的值小于左右结点
(2)图解算法
下面就以大根堆为例,先来看看如何用代码构建一个大根堆
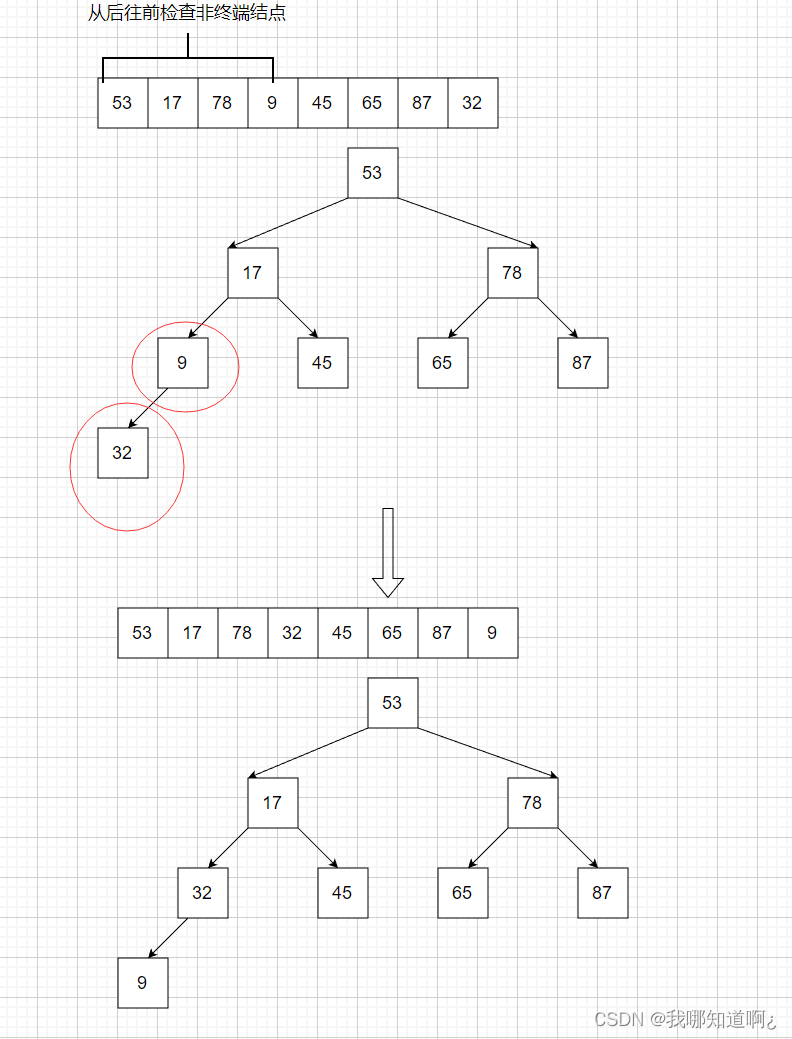
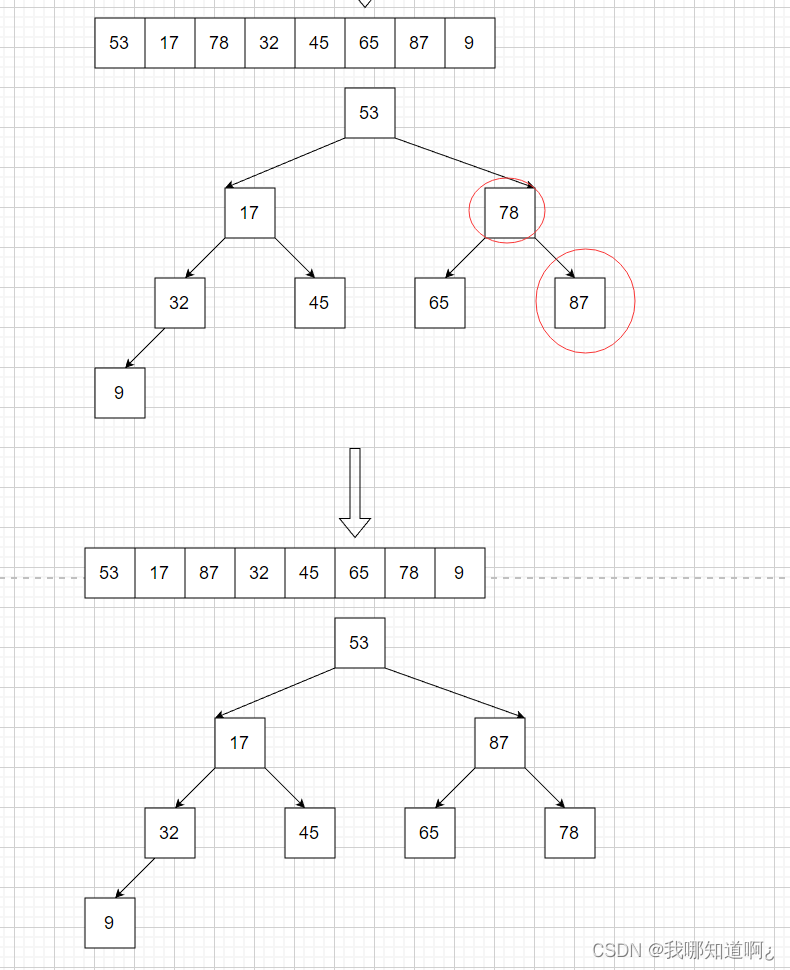
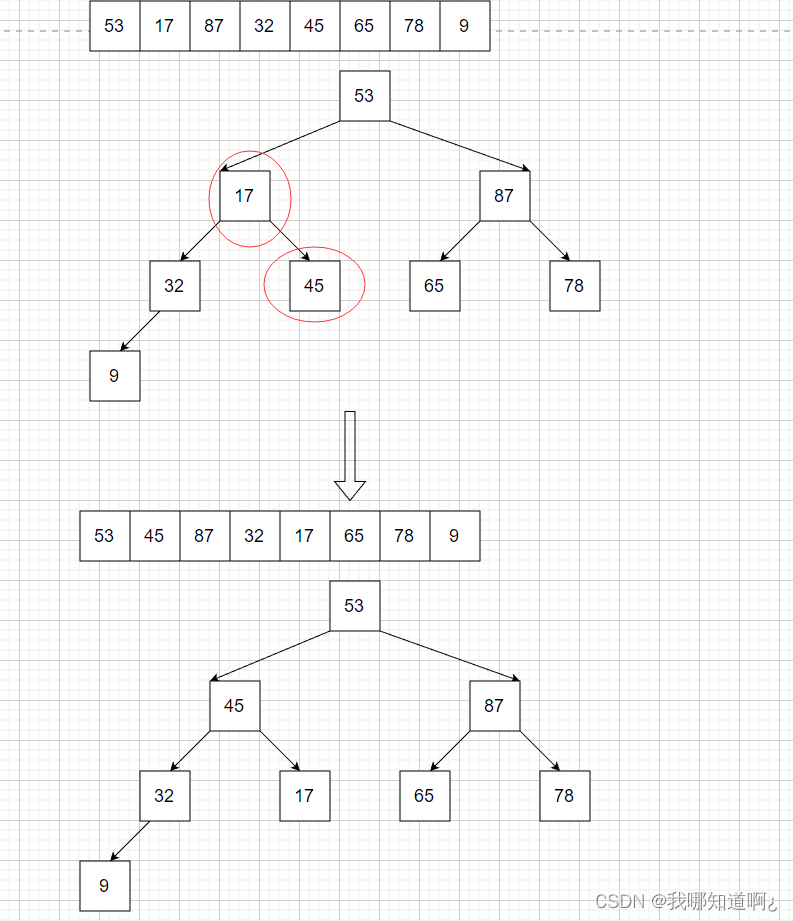
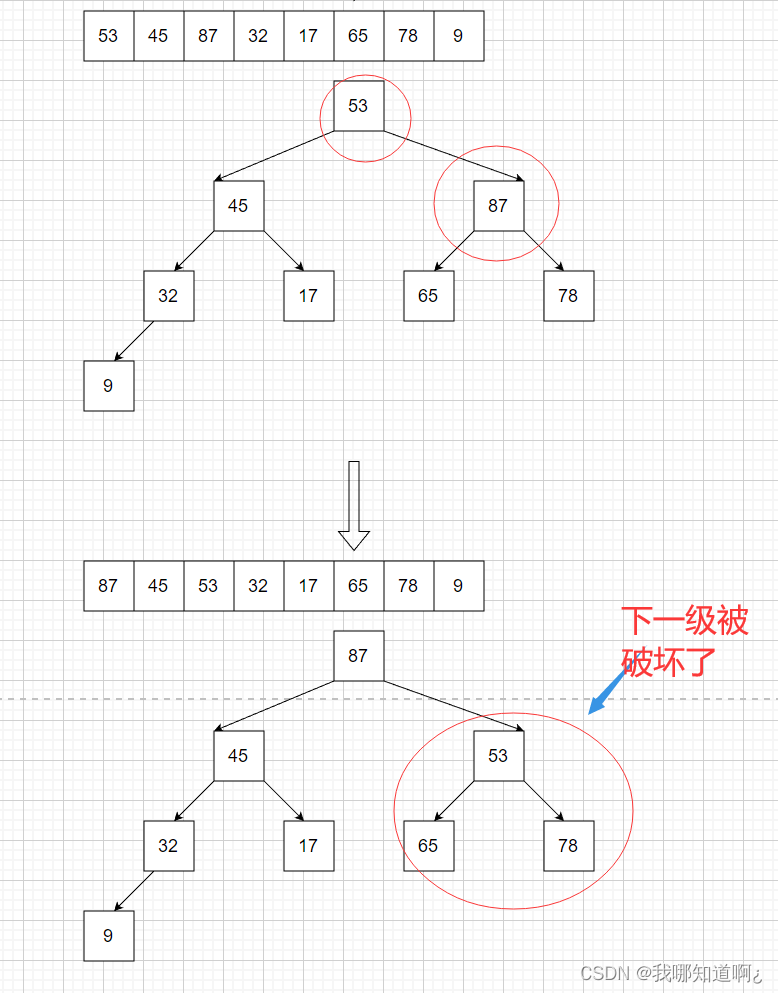
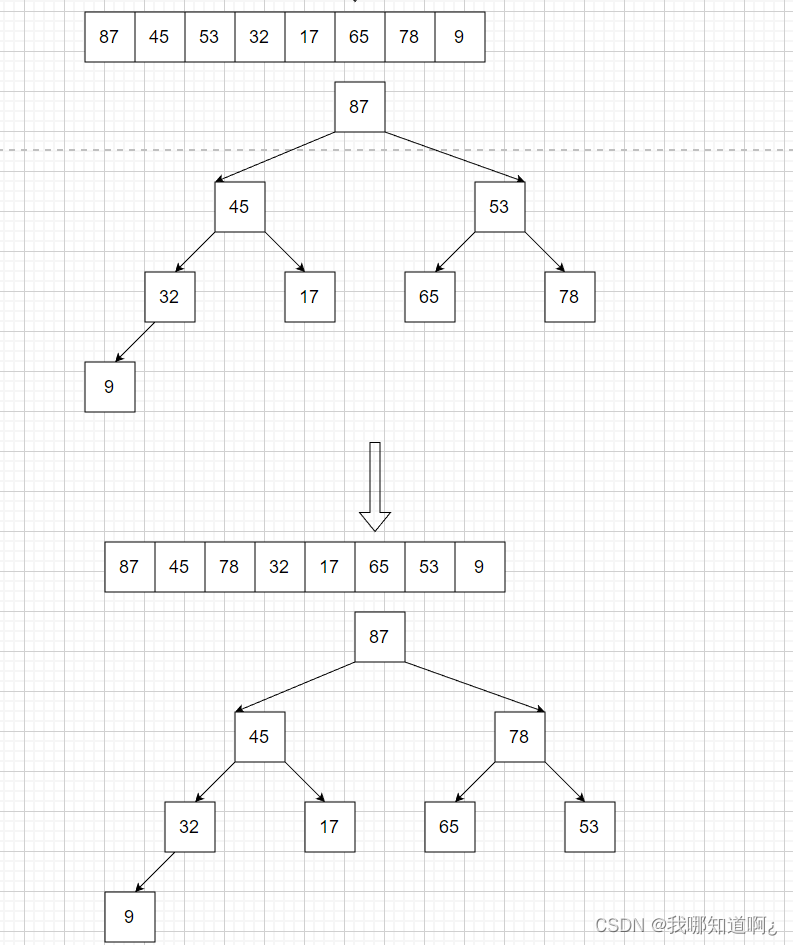
那么接下来怎么基于大根堆进行选择排序呢?
因为已经构造好了大根堆,那么此时序列的最大值就是堆顶的根节点,我们将其和末尾元素交换,此时末尾元素就是最大值,然后将剩下的n-1个元素再调整成大根堆,如此反复执行,就可以得到一个有序序列了
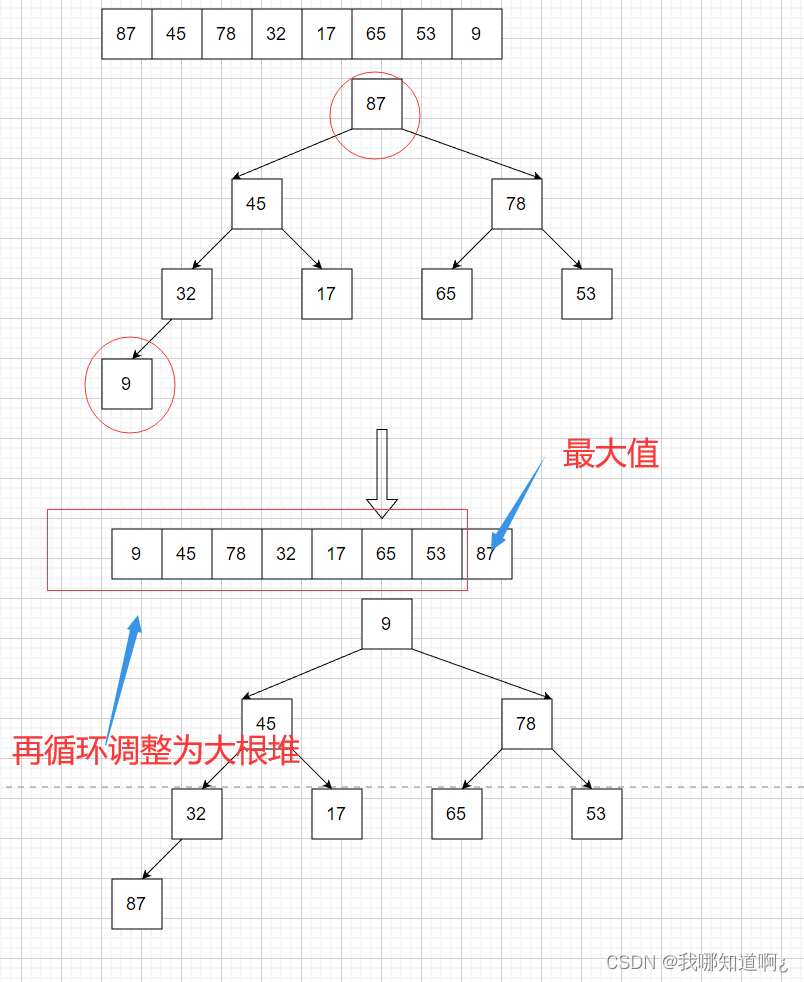
(3)代码实现
//堆排序
public void heapSort(int[] nums){
//建立大根堆
buildMaxHeap(nums);
//基于大根堆的选择排序,交换首尾元素后再调整
for (int i = nums.length-1; i >0; i--) {
int temp = nums[0];
nums[0]=nums[i];
nums[i]=temp;
headAdjust(nums,0,i);
}
}
private void buildMaxHeap(int[] nums) {
for (int i = nums.length/2-1; i >=0; i--) {
headAdjust(nums,i,nums.length);
}
}
//将以k为根的子树调整为大根堆
private void headAdjust(int[] nums, int i, int length) {
//暂存当前待调整结点的元素
int temp = nums[i];
//从节点的左孩子开始,下标2i+1
for (int j = i*2+1; j <length; j=j*2+1) {
//左结点小于右结点,那么就指向更大的右结点
if (j+1<length && nums[j]<nums[j+1]) j++;
//子节点的值大于父节点,就将子节点的值赋值给父节点
if (nums[j]>temp){
nums[i]=nums[j];
//继续调整子节点
i=j;
}else {
//子节点的值不大于父节点,说明无须调整
break;
}
}
nums[i]=temp;//最后把temp放到他最终的位置
}
(4)算法效率分析
空间复杂度:1
时间复杂度:
- 建堆的时间复杂度:O(n)
- 排序的过程O(log2n)
- 整体时间复杂度:O(nlog2n)
归并排序
(1)基础概念
把两个或者多个已经有序的序列合并成一个
合并两个有序的序列:使用双指针,指向两个序列的第一个元素,然后不断对比大小关系,每次都将较小的那个移动到新数组中,不断迭代,合并两个也叫二路归并
那么如果有多个序列,也就是使用多指针的方式
如果是m路归并,每选出一个元素要对比关键字m-1次
(2)图解算法
在这里,我们主要使用二路归并,刚刚开始,数组中的每一个元素都视为是有序的
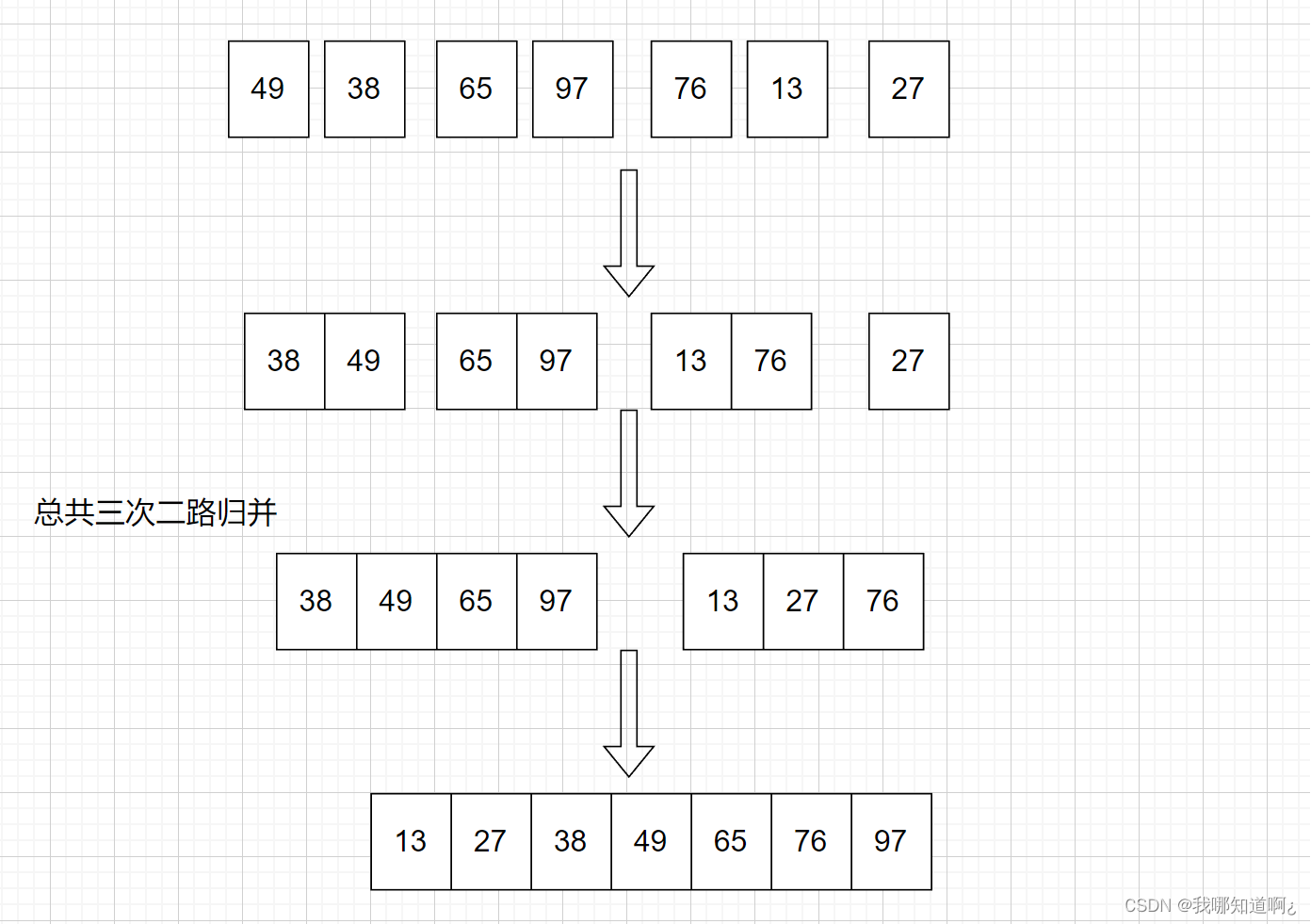
(3)代码实现
public void mergeSort(int[] nums, int low, int high){
if (low<high){
//从中间划分数组
int mid = (low+high)/2;
//对左半部分进行归并
mergeSort(nums,low,mid);
//对右半部分进行归并
mergeSort(nums,mid+1,high);
//归并
merge(nums,low,mid,high);
}
}
private void merge(int[] nums, int low, int mid, int high) {
int[] temp = new int[nums.length];//辅助数组,这个辅助数组应该通过传参或者外部定义,这里为了代码的直观就直接new了
//[low,mid][mid+1,high]各自有序,将两个部分归并
//先把当前的所有元素全部复制到temp中
for (int i = low; i <=high; i++) {
temp[i]=nums[i];
}
int i = low;
int j = mid+1;
int k = low;
//接下来二路归并到原数组中
while (i<=mid && j<=high){
if (temp[i]<=temp[j]){
nums[k]=temp[i];
i++;
}else {
nums[k]=temp[j];
j++;
}
k++;
}
while (i<=mid) nums[k++]=temp[i++];
while (j<=high) nums[k++]=temp[j++];
}
(4)算法效率分析
空间复杂度:O(n),来自于辅助数组
时间复杂度:n个元素进行二路归并,一共需要log2n趟,每趟的时间复杂度为O(n),时间复杂度为O(nlog2n)






![基于gin-vue-admin[gin+gorm]手动实现crud(全)](https://img-blog.csdnimg.cn/8c43b1cc45084e648a4e85e060c58402.png)