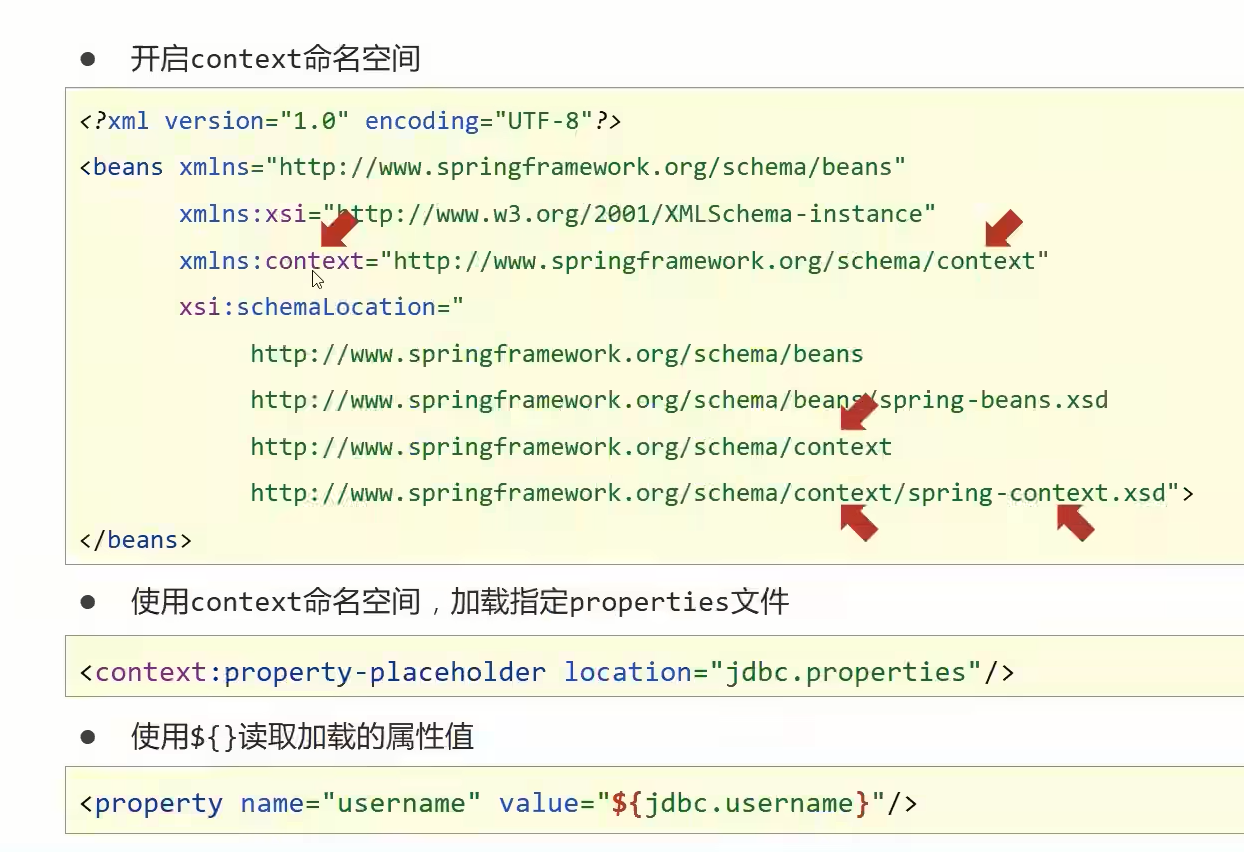
在线测试

Project #3 - Query Execution

以下是Project #3的网址，2022FALL的Project #3是实现一个查询执行，实现一系列算子，用于实现数据库内的SQL计算。项目中的 Query Execution 主要分为三个任务：

1. Access Method Executors ： 需要实现 SeqScan、Insert、Delete、IndexScan 四个算子。
2. Aggregation and Join Executors ： 需要实现 Aggregation、NestedLoopJoin、NestedIndexJoin 三个算子。
3. Sort + Limit Executors and Top-N Optimization ： 需要实现 Sort、Limit、TopN 三个算子，以及实现将 Sort + Limit 优化为 TopN 算子。

我们首先需要了解 SQL 语句如何在 Bustub 中实现相应功能：

1. 一条 SQL 语句首先通过 Parser 生成一棵抽象语法树 AST 。在 Bustub 中通过调用第三方库libpg_query 将一条 SQL 语句解析为 AST 。
2. 在获得 AST 之后， Binder 将抽象的词语绑定到数据库中的实体类中，最终获得一个可以被 Bustub 理解的 Bustub AST 。
3. 获得了绑定的语法树之后，Planner 遍历这棵树，生成相应的查询计划。我们可以将 Planner 理解为树中的每一个节点，需要根据查询计划进行一定的运算。
4. 在通过 Planner 获得了初步查询计划之后，我们还可以通过 Optimizer 进行优化，提升查询的效率，并生成最终查询计划。
5. 在确定了最终的查询计划之后，我们需要通过 Executor 实现最终的算子，利用算子来真正实现我们的查询计划，将原先的 PlanNode 更换成我们实现的 Executor ，这也是我们本部分的主要内容。

值得注意的是，在 Bustub 中，对于实现 Optimizer ，我们在遍历 Planner 生成的初步查询计划时，利用预先设定的规则实现对 PlanNode 的优化，如将 Limit + Sort 合并为 TopN ，这需要我们提前设定好规则；对于实现 Executor ，我们采用 Iterator Model （火山模型），其中每个算子内部的 Init()实现算子的初始化，Next()用于向子节点请求数据，其中，火山模型的优点在于占用内存较小，一次只使用一条数据，但这也导致我们会频繁调用函数，特别是虚函数，带来较大开销，而我们在执行查询时，也是自上向下请求数据。最终，当根节点获得了所有需要查询的数据时，就实现了 SQL 语句的功能。

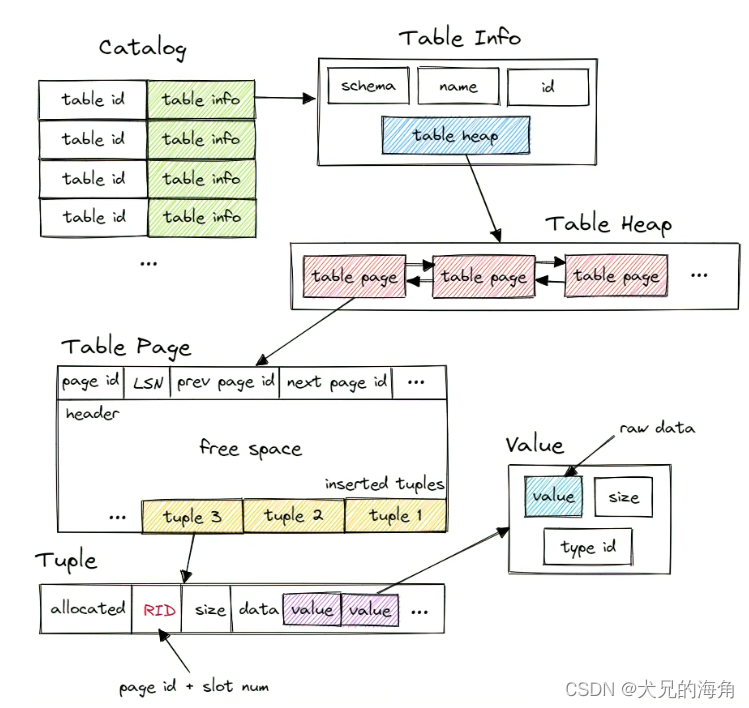
在 Bustub 中，有一个 Catalog 用于保存 table 的一系列信息，其中需要维护从 table id 和 table name 到 table info 的映射关系，从而可以通过相应键进行查询。
在 table info 中保存了一张表的模式、名字、id 和指向 table heap 的指针。
在 table heap 中有着一系列的 table page ，构成了双向链表的结构，能够遍历整张表获取相应的信息，而 table heap 仅保存其中第一个 table page 的 page id 。
在 table page 内部，他是 page 的一个子类，其中，真正储存了数据的 tuple 从高地址开始向 table page 尾部进行插入。
储存数据的 tuple 对应着表中的一行数据，每个 tuple 都有 RID 唯一对应，其中 RID 由
page id + slot num 构成，而其中的 value 则是每个字段的具体值，由 table info 中的模式来决定。

任务 #1 - 访问方法执行程序

对于任务一，我们需要实现四个算子：SeqScanExecutor 、InsertExecutor 、DeleteExecutor 、IndexScanExecutor 。

SeqScanExecutor

SeqScanExecutor 的功能是需要实现读取给定 table 中的所有 tuple 。在构造函数SeqScanExecutor中，我们利用GetCatalog获得 Bustub 中的 Catalog ，并根据table_oid_利用GetTable获得对应的table_info_，从而获得后续的存放表的 page 。在Init中，我们将当前 table 的指针指向初始的 begin 位置。在Next函数中，我们首先判断当前 table 的迭代器是否指向末尾，若是则直接返回 false 。而后我们利用指针直接获得当前迭代器对应的 tuple ，并更新 tuple 相应的 rid ，最终移动迭代器。

InsertExecutor

InsertExecutor 的功能是根据子节点算子的结果向当前表中插入项。在构造函数InsertExecutor中，我们同样利用GetCatalog获得 Bustub 中的 Catalog ，并根据table_oid_利用GetTable获得对应的table_info_，从而获得后续的存放表的 page 。值得注意的是，由于此处子算子使用的是 unique_ptr ，因此我们在初始化时不能复制只能使用std::move。在Init中，我们首先需要初始化子算子，而后考虑到我们插入项之后可能会影响到当前表中已经存在的索引，我们需要根据当前的 table_info_ 获取相应的索引列表。在Next函数中，我们首先从子算子中获得我们需要插入的 tuple 和对应的 RID 。而后我们利用InsertTuple向对应的表中插入 tuple 。若插入成功，我们需要遍历当前表中的所有索引，并将新插入的记录插入索引中。最终，我们将插入的内容和对应的模式储存到 tuple 并返回 true ，其中 tuple 中会包含一个 integer value 用于表示由多少行受到影响。

DeleteExecutor

DeleteExecutor 的功能是根据子节点算子的结果向当前表中删除项。在构造函数DeleteExecutor中，我们同样利用GetCatalog获得 Bustub 中的 Catalog ，并根据table_oid_利用GetTable获得对应的table_info_，从而获得后续的存放表的 page 。在Init中，我们首先需要初始化子算子，而后考虑到我们删除项之后可能会影响到当前表中已经存在的索引，我们需要根据当前的 table_info_ 获取相应的索引列表。在Next函数中，我们首先从子算子中获得我们需要删除的 tuple 和对应的 RID 。而后我们利用MarkDelete向对应的表中删除 tuple ，值得注意的是，在 Bustub 中，我们并不是在此时直接删除，而是将 tuple 标记为删除状态，也就是逻辑删除。若删除成功，我们需要遍历当前表中的所有索引，并在索引中删除对应的项。最终，我们将删除的内容和对应的模式储存到 tuple 并返回 true ，其中 tuple 中会包含一个 integer value 用于表示由多少行受到影响。

IndexScanExecutor

IndexScanExecutor 的功能是根据 Project 2 中实现的 B+ 树索引，遍历叶子节点查找我们需要的项。由于我们实现的是非聚簇索引，在叶子节点只能获取到 RID，需要拿着 RID 去 table 查询对应的 tuple。在构造函数IndexScanExecutor中，我们同样利用GetCatalog获得 Bustub 中的 Catalog ，并根据table_oid_利用GetTable获得对应的table_info_，从而获得后续的存放表的 page ，同时我们还需要初始化需要使用的 table_info_ 、tree_ 、iter_ 。在Init中，我们需要初始化的内容都已经在构造函数中得到初始化。在Next函数中，我们首先判断当前 B+ 树的指针是否指向树的末尾，若是则直接返回 false 。否则我们获得当前指针对应的节点的 RID ，并从 table_ 中获得对应的 tuple ，移动指针并返回结果。

任务 #2 - 聚合和加入执行程序

对于任务二，我们需要实现三个算子：AggregationExecutor、NestedLoopJoinExecutor、NestIndexJoinExecutor 。

AggregationExecutor

AggregationExecutor 的功能是实现一个聚集功能，考虑到我们可能会对某一列上的元素进行一些常见的操作，我们可以利用聚集函数直接获得相应值而不需要一个个去遍历计算。在 Bustub 中，我们利用哈希表来储存需要 group by 的字段的数组和需要 aggregate 的字段的数组。因此，我们需要在Init中便计算出所有结果并进行暂存，而在Next中将获得的结果一条条 emit 。在构造函数AggregationExecutor中，我们对所有使用到的 plan 节点、子算子节点、哈希表、哈希表指针进行初始化。在Init中，我们根据子算子中 emit 的记录调用InsertCombine插入我们维护的哈希表中，若最终哈希表为空或只有一列属性则添加初值，最终初始化哈希表的指针。此外，我们还需要实现CombineAggregateValues，根据我们需要执行的聚集函数，包括 count(*) 、count 、sum 、min 、max ，并将计算出的结果储存到哈希表中。在Next中，我们首先判断当前哈希表的指针是否指向末尾，若是则直接返回 false 。而后我们输出当前的键值对并附上模式，移动迭代器后返回。

NestedLoopJoinExecutor

NestedLoopJoinExecutor 的功能是实现一个连表功能，其特点在于将外表中的每一条 tuple 与内表中的每一条 tuple 进行比较，在内表循环完成之后读取外表的下一条 tuple ，效率比较低。在构造函数NestedLoopJoinExecutor中，我们初始化对应的 plan 节点、左子算子和右子算子。在Init中，我们初始化左右算子并将右子算子的内容全部压入数组中。在Next中，我们将左子算子此时 emit 的 tuple 与右子算子返回的数组中的每一条利用EvaluateJoin进行比较，若匹配则将连表后的新 tuple 压入最终结果的数组中。若此时是左连表，则将左表中的内容和右表中的内容或空内容压入最终结果中。值得注意的是，为了避免右子算子的结果被全部使用后只会返回 false 的情况，我们使用数组提前储存右子算子中的所有结果。同时为了避免左子算子的结果可能与右子算子中的多个 tuple 相匹配的情况，我们在算子中暂存左子算子的结果并优先尝试进行匹配，此外我们还记录在右子算子的列表中上一次匹配的结果。若遍历右子算子的列表仍未匹配，再去要求左子算子传来下一个 tuple 。

NestIndexJoinExecutor

NestIndexJoinExecutor的功能是实现一个连表功能，与上一功能的区别在于我们直接使用索引进行查询，能够大大加快速度。若现 JOIN ON 右边的字段上建了 index，则 Optimizer 会将 NestedLoopJoin 优化为 NestedIndexJoin。在构造函数NestedLoopJoinExecutor中，我们初始化对应的 plan 节点、子算子和索引信息、表信息和 B+ 树。在Next中，我们首先获得子算子中的 tuple ，而后在对内表进行匹配时，直接使用 tuple 中储存的信息在索引中进行搜索，并返回相应的结果。

任务 #3 - 排序 + 限制执行程序和 top-N 优化

对于任务三，我们需要实现三个算子：SortExecutor、LimitExecutor、TopNExecutor ，同时优化 Optimize ，将连续出现的 limit 和 sort 的 plan 节点直接优化 topn 节点。

SortExecutor

SortExecutor的功能是按 ORDER BY 的字段升序或降序排序。在构造函数SortExecutor中，我们初始化当前的 plan 节点和子算子。在Init中，我们首先将子算子 emit 的结果全部压入数组中。而后我们利用std::sort实现对数组的排序，其中需要我们调用CompareGreaterThan实现对于元素的比较。在Next中，我们返回当前的 tuple 与 RID 并移动迭代器。

LimitExecutor

LimitExecutor的功能是利用自己维护的变量 count 记录当前已经 emit 多少个 tuple 。若下层算子为空或 count 抵达上限则不再进行 emit 。在构造函数LimitExecutor中，我们初始化当前的 plan 节点和子算子。在Init中，我们初始化子算子与 count_ 。在Next中，我们判断子算子是否还能 emit 或当前的 count_ 是否超过上限。

TopNExecutor

TopNExecutor的功能是计算当前排序的前 N 个 tuple 。我们只需要将以上两个算子相结合，先排序后输出前 N 个 tuple 即可。

Sort + Limit As TopN

此处我们需要优化 Optimize ，将连续出现的 limit 和 sort 的 plan 节点直接优化 topn 节点。我们需要实现 OptimizeSortLimitAsTopN ，其中我们首先获得当前节点的所有子算子节点并递归调用函数 OptimizeSortLimitAsTopN ，而后我们将优化后的子算子加入数组，并克隆一个新的子算子用于修改。而后我们首先判断当前的子节点是否为 Limit ，而子节点的子节点是否为 Sort ，只有严格按照这个格式我们才能够确定可以使用 TopNPlanNode 代替这两个节点。

值得注意的是，在利用规则对当前的原始 plan 树进行优化时，我们实际上是对当前树进行后续遍历，自底向上使用规则来改写节点。若我们当前的遍历的节点满足我们的改写条件则对当前的树进行优化。