什么是 Diffusion Model

一、前向 Diffusion 过程

Diffusion Model 首先定义了一个前向扩散过程，总共包含T个时间步，如下图所示：

最左边的蓝色圆圈 x0 表示真实自然图像，对应下方的狗子图片。

最右边的蓝色圆圈 xT 则表示纯高斯噪声，对应下方的噪声图片。

最中间的蓝色圆圈 xt 则表示加了噪声的 x0 ，对应下方加了噪声的狗子图片。

箭头下方的 q(xt|xt-1) 则表示一个以前一个状态 xt-1 为均值的高斯分布，xt  从这个高斯分布中采样得到。

所谓前向扩散过程可以理解为一个马尔可夫链[7]，即通过逐步对一张真实图片添加高斯噪声直到最终变成纯高斯噪声图片。

（1）利用前一时刻的 xt-1 得到任意时刻的噪声图片 xt（重参数化技巧）

那么具体是怎么添加噪声呢，公式表示如下：

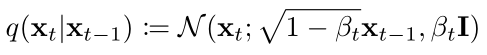
★★★ 也就是每一时间步的 xt 是从一个，以 1-βt 开根号乘以 xt-1 为均值，βt为方差的高斯分布中采样得到的。其中βt, t ∈ [1, T] 是一系列固定的值，由一个公式生成。

在参考资料 [2] 中设置 T=1000, β1=0.0001, βT=0.02，并通过一句代码生成所有 βt 的值：

# https://pytorch.org/docs/stable/generated/torch.linspace.html
betas = torch.linspace(start=0.0001, end=0.02, steps=1000)

然后在采样得到 xt 的时候并不是直接通过高斯分布 q(xt|xt-1) 采样，而是用了一个重参数化的技巧（详见参考资料[4]第5页）。

★★★ 简单来说就是，如果想要从一个任意的均值 μ 方差 σ^2 的高斯分布中采样得到xt：

1）可以首先从一个标准高斯分布（均值0，方差1）中进行采样得到噪声 ε，

noise = torch.randn_like(x_0)

2）然后利用 μ + σ·ε 就等价于从任意均值 μ 方差 σ^2 的高斯分布中采样（首先从标准高斯分布中采样得到噪声 ε，接着乘以标准差再加上均值）。公式表示如下：

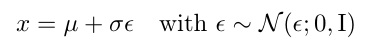
xt = sqrt(1-betas[t]) * xt-1 + sqrt(betas[t]) * noise

 完整代码：

# https://pytorch.org/docs/stable/generated/torch.randn_like.html
betas = torch.linspace(start=0.0001, end=0.02, steps=1000)
noise = torch.randn_like(x_0)
xt = sqrt(1-betas[t]) * xt-1 + sqrt(betas[t]) * noise

（2）直接从 x0 采样得到中间任意一个时间步的噪声图片 xt

然后前向扩散过程还有个属性，就是可以直接从 x0 采样得到中间任意一个时间步的噪声图片 xt，公式如下：

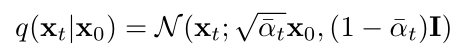
其中的 αt 表示：

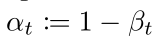
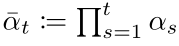
具体怎么推导出来的可以看参考资料[4] 第11页，伪代码表示如下：

betas = torch.linspace(start=0.0001, end=0.02, steps=1000)
alphas = 1 - betas
# cumprod 相当于为每个时间步 t 计算一个数组 alphas 的前缀乘结果
# https://pytorch.org/docs/stable/generated/torch.cumprod.html
alphas_cum = torch.cumprod(alphas, 0)
alphas_cum_s = torch.sqrt(alphas_cum)
alphas_cum_sm = torch.sqrt(1 - alphas_cum)

# 应用重参数化技巧采样得到 xt
noise = torch.randn_like(x_0)
xt = alphas_cum_s[t] * x_0 + alphas_cum_sm[t] * noise

通过上述的讲解，读者应该对 Diffusion Model 的前向扩散过程有比较清晰的理解了。

不过我们的目的不是要做图像生成吗？现在只是从数据集中的真实图片得到一张噪声图，那具体是怎么做图像生成呢？

二、反向 Diffusion 过程

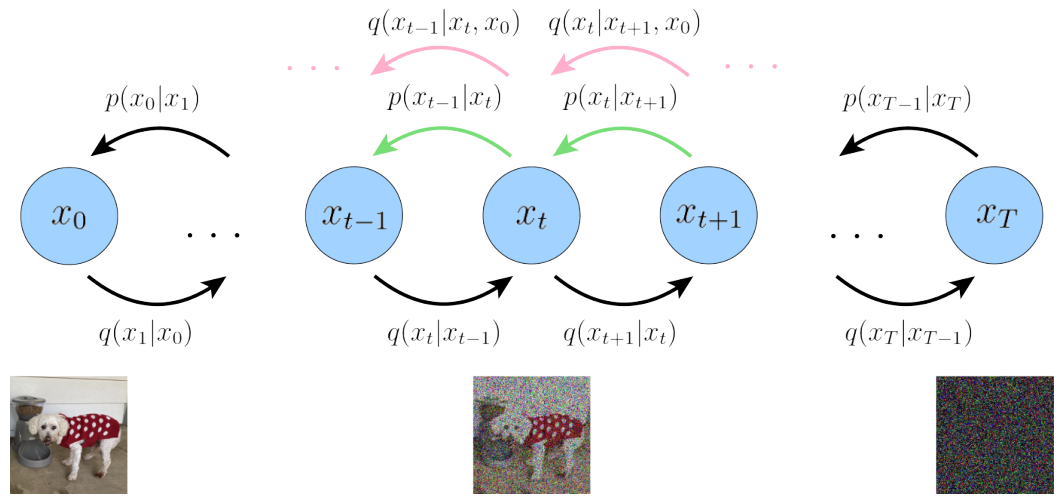
反向扩散过程 q(xt-1|xt, x0) （看粉色箭头）是前向扩散过程 q(xt|xt-1) 的后验概率分布。

和前向过程相反是从最右边的纯高斯噪声图，逐步采样得到真实图像 x0。

后验概率 q(xt-1|xt, x0) 的形式可以根据贝叶斯公式推导得到（推导过程详见参考资料[4]第12页）：

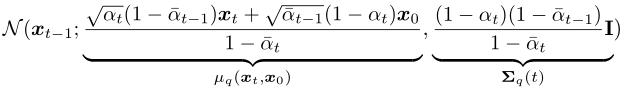
也是一个高斯分布。

（1）方差：

其方差从公式上看是个常量，所有时间步的方差值都是可以提前计算得到的：

betas = torch.linspace(start=0.0001, end=0.02, steps=1000)
alphas = 1 - betas
alphas_cum = torch.cumprod(alphas, 0)
alphas_cum_prev = torch.cat((torch.tensor([1.0]), alphas_cum[:-1]), 0)
posterior_variance = betas * (1 - alphas_cum_prev) / (1 - alphas_cum)

（2）均值：

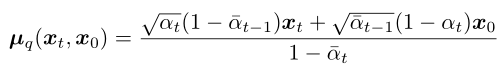
对于反向扩散过程，在采样生成 xt-1 的时候 xt 是已知的，而其他系数都是可以提前计算得到的常量。

但是现在问题来了，在真正通过反向过程生成图像的时候，x0 我们是不知道的，因为这是待生成的目标图像。

好像变成了鸡生蛋，蛋生鸡的问题，那该怎么办呢？

（3）Diffusion Model 训练目标

当一个概率分布q 求解困难的时候，我们可以换个思路（详见参考资料[5,6]）。

通过人为构造一个新的分布 p，然后目标就转为缩小分布 p 和  q 之间差距。通过不断修改 p  的参数去缩小差距，当 p 和 q 足够相似的时候就可以替代 q 了。

然后回到反向 Diffusion 过程，由于后验分布 q(xt-1|xt, x0) 没法直接求解。

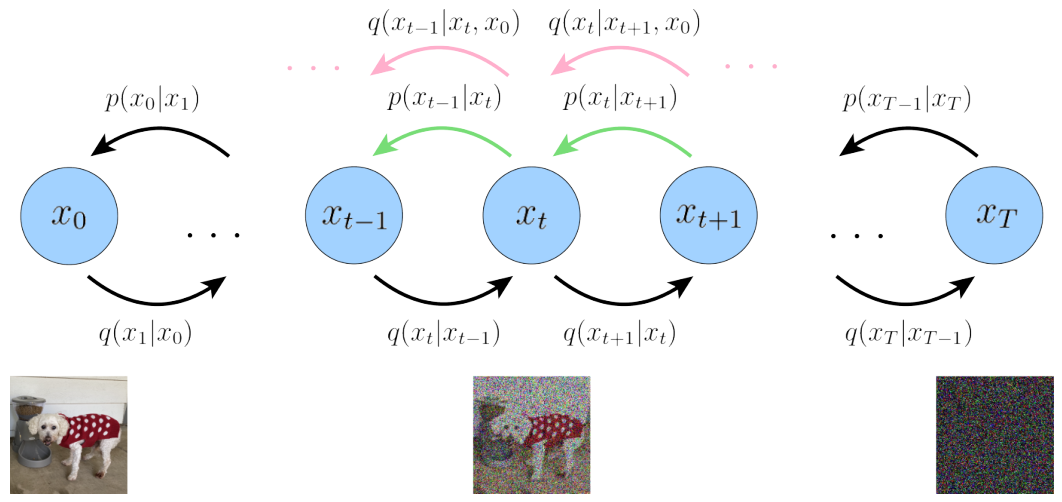
那么我们就构造一个高斯分布 p(xt-1|xt)（见绿色箭头），让其方差和后验分布  q(xt-1|xt, x0) 一致：

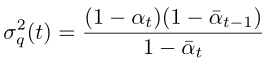
而其均值则设为：

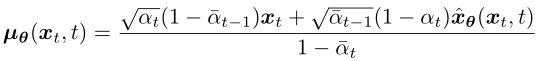
和 q(xt-1|xt, x0) 的区别在于，x0 改为 xθ(xt, t) 由一个深度学习模型预测得到，模型输入是噪声图像 xt 和时间步 t 。

然后缩小分布  p(xt-1|xt) 和  q(xt-1|xt, x0) 之间差距，变成优化以下目标函数（推导过程详见参考资料[4]第13页）：

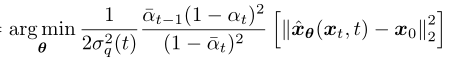
但是如果让模型直接从 xt 去预测 x0，这个拟合难度太高了，我们再继续换个思路。

前面介绍前向扩散过程提到，xt 可以直接从 x0 得到：

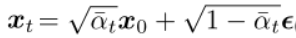
将上面的公式变换一下形式：

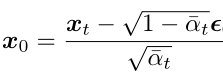
代入上面  q(xt-1|xt, x0) 的均值式子中可得（推导过程详见参考资料[4]第15页）：

观察上述变换后的式子，发现后验概率 q(xt-1|xt, x0) 的均值只和 xt 和前向扩散时候时间步 t 所加的噪声有关。

所以我们同样对构造的分布 p(xt-1|xt) 的均值做一下修改：

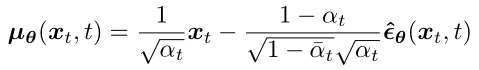
将模型改为去预测在前向时间步 t 所添加的高斯噪声 ε，模型输入是 xt 和 时间步 t：

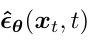
接着优化的目标函数就变为（推导过程详见参考资料[4]第15页）：

然后训练过程算法描述如下，最终的目标函数前面的系数都去掉了，因为是常量：

★ 可以看到虽然前面的推导过程很复杂，但是训练过程却很简单：

1. 首先每个迭代就是从数据集中取真实图像 x0，并从均匀分布中采样一个时间步 t，
2. 然后从标准高斯分布中采样得到噪声 ε，并根据公式计算得到前向过程的 xt。
3. 接着将 xt 和 t 输入到模型让其输出去拟合预测噪声 ε，并通过梯度下降更新模型，一直循环直到模型收敛。
4. 而采用的深度学习模型是类似 UNet 的结构（详见参考资料[2]附录B）。

训练过程的伪代码如下：

betas = torch.linspace(start=0.0001, end=0.02, steps=1000)
alphas = 1 - betas
alphas_cum = torch.cumprod(alphas, 0)
alphas_cum_s = torch.sqrt(alphas_cum)
alphas_cum_sm = torch.sqrt(1 - alphas_cum)

def diffusion_loss(model, x0, t, noise):
    # 根据公式计算 xt
    xt = alphas_cum_s[t] * x0 + alphas_cum_sm[t] * noise
    # 模型预测噪声
    predicted_noise = model(xt, t)
    # 计算Loss
    return mse_loss(predicted_noise, noise)

for i in len(data_loader):
    # 从数据集读取一个 batch 的真实图片
    x0 = next(data_loader)
    # 采样时间步
    t = torch.randint(0, 1000, (batch_size,))
    # 生成高斯噪声
    noise = torch.randn_like(x_0)
    loss = diffusion_loss(model, x0, t, noise)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

三、Diffusion Model 生成图像过程

模型训练好之后，在真实的推理阶段就必须从时间步 T 开始往前逐步生成图片，算法描述如下：

步骤：

1. 一开始先生成一个从标准高斯分布生成噪声，
2. 然后每个时间步 t，将上一步生成的图片 xt 输入模型模型预测出噪声。
3. 接着从标准高斯分布中采样一个噪声，根据重参数化技巧，后验概率的均值和方差公式，计算得到 xt-1，直到时间步 1 为止。

四、改进 Diffusion Model

文章 [3] 中对 Diffusion Model 提出了一些改进点。

（1）对方差 βt  的改进

前面提到 βt 的生成是将一个给定范围均匀的分成 T 份，然后每个时间步对应其中的某个点：

betas = torch.linspace(start=0.0001, end=0.02, steps=1000)

然后文章 [3] 通过实验观察发现，采用这种方式生成方差 βt 会导致一个问题，就是做前向扩散的时候到靠后的时间步噪声加的太多了。

这样导致的结果就是在前向过程靠后的时间步，在反向生成采样的时候并没有产生太大的贡献，即使跳过也不会对生成结果有多大的影响。

接着论文[3] 中就提出了新的 βt 生成策略，和原策略在前向扩散的对比如下图所示：

第一行就是原本的生成策略，可以看到还没到最后的时间步就已经变成纯高斯噪声了，而第二行改进的策略，添加噪声的速度慢一些，看起来也更合理。

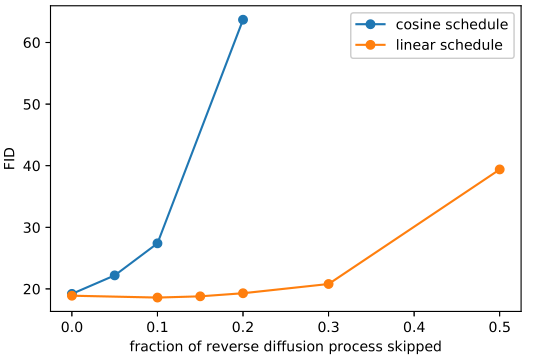
实验结果表明，针对 imagenet 数据集 64x64 的图片，原始的策略在做反向扩散的时候，即使跳过开头的 20% 的时间步，都不会对指标有很大的影响。

然后看下新提出的策略公式：

其中 s 设置为 0.008同时限制 βt最大值为 0.999，伪代码如下：

T = 1000
s = 8e-3
ts = torch.arange(T + 1, dtype=torch.float64) / T + s
alphas = ts / (1 + s) * math.pi / 2
alphas = torch.cos(alphas).pow(2)
alphas = alphas / alphas[0]
betas = 1 - alphas[1:] / alphas[:-1]
betas = betas.clamp(max=0.999)

（2）对生成过程时间步数的改进

原本模型训练的时候是假定在 T个时间步下训练的，在生成图像的时候，也必须从 T 开始遍历到 1 。而论文 [3] 中提出了一种不需要重新训练就可以减少生成步数的方法，从而显著提升生成的速度。

这个方法简单描述就是，原来是 T 个时间步现在设置一个更小的时间步数 S ，将 S 时间序列中的每一个时间步 s 和 T时间序列中的步数 t 对应起来，伪代码如下：

T = 1000
S = 100
start_idx = 0
all_steps = []
frac_stride = (T - 1) / (S - 1)
cur_idx = 0.0
s_timesteps = []
for _ in range(S):
    s_timesteps.append(start_idx + round(cur_idx))
    cur_idx += frac_stride

接着计算新的 β ，St 就是上面计算得到的 s_timesteps：

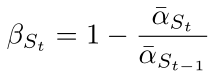
伪代码如下：

alphas = 1 - betas
alphas_cum = torch.cumprod(alphas, 0)
last_alpha_cum = 1.0
new_betas = []
# 遍历原来的 alpha 前缀乘序列
for i, alpha_cum in enumerate(alphas_cum):
    # 当原序列 T 的索引 i 在新序列 S 中时，计算新的 beta
    if i in s_timesteps:
        new_betas.append(1 - alpha_cum / last_alpha_cum)
        last_alpha_cum = alpha_cum

简单看下实验结果：

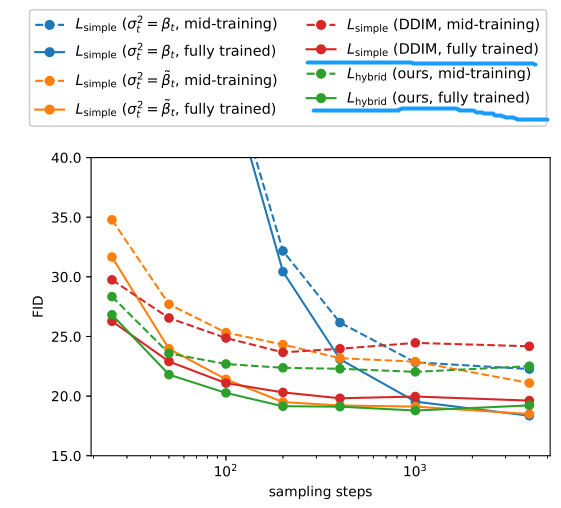
关注画蓝线的红色和绿色实线，可以看到采样步数从 1000 缩小到 100 指标也没有降多少。

参考资料

• [1] https://www.assemblyai.com/blog/diffusion-models-for-machine-learning-introduction/

• [2] https://arxiv.org/pdf/2006.11239.pdf

• [3] https://arxiv.org/pdf/2102.09672.pdf

• [4] https://arxiv.org/pdf/2208.11970.pdf

• [5] https://www.zhihu.com/question/41765860/answer/1149453776

• [6] https://www.zhihu.com/question/41765860/answer/331070683

• [7] https://zh.wikipedia.org/wiki/%E9%A9%AC%E5%B0%94%E5%8F%AF%E5%A4%AB%E9%93%BE

• [8] https://github.com/rosinality/denoising-diffusion-pytorch

• [9] https://github.com/openai/improved-diffusion

一文弄懂 Diffusion Model