这学期会时不时更新一下伊曼纽尔·德曼（Emanuel Derman） 教授与迈克尔B.米勒（Michael B. Miller）的《The Volatility Smile》这本书，本意是协助导师课程需要，发在这里有意的朋友们可以学习一下，思路不一定够清晰且由于分工原因我是从书本第13章写起，还请大家见谅。

第14章 局部波动率模型

股价变动方式的二叉树模型

上一章前瞻波动率 $\sigma (t)$​ 的推导：
$${\sum }^2(t,T)=\frac{1}{T-t}{\int }_t^T{\sigma }^2(s)ds$$
$\sigma (t)$ 会随时间变化而变化，同样地，波动率 $\sigma (S,t)$ 也会随未来的时间和股票价格两个参数的变化而变化。

我们将这种瞬时波动率 $\sigma (S,t)$ 称为局部波动率，以此为基础建立的模型被称为局部波动率模型。

开发局部波动率模型时需要关注的问题：

1. 能否找到独一无二的局部波动率函数或者曲面 $\sigma (S,t)$，使其能够描述观察到的隐含波动率曲面 $\sum (S,t,K,T)$？如果可以，这就意味着我们可以用一个股票的局部波动率过程来解释观察到的微笑曲线
2. 但是这样的解释是否有意义？股票价格的变动真的会服从这个已经存在的局部波动率函数？我们将会发现，有很多不同的模型都能够描述隐含波动率曲面，但这并不意味着这些模型是“正确的”
3. 局部波动率模型如何确定普通期权的对冲比率以及奇异期权的价值？其结论和经典的BSM模型有何差异？

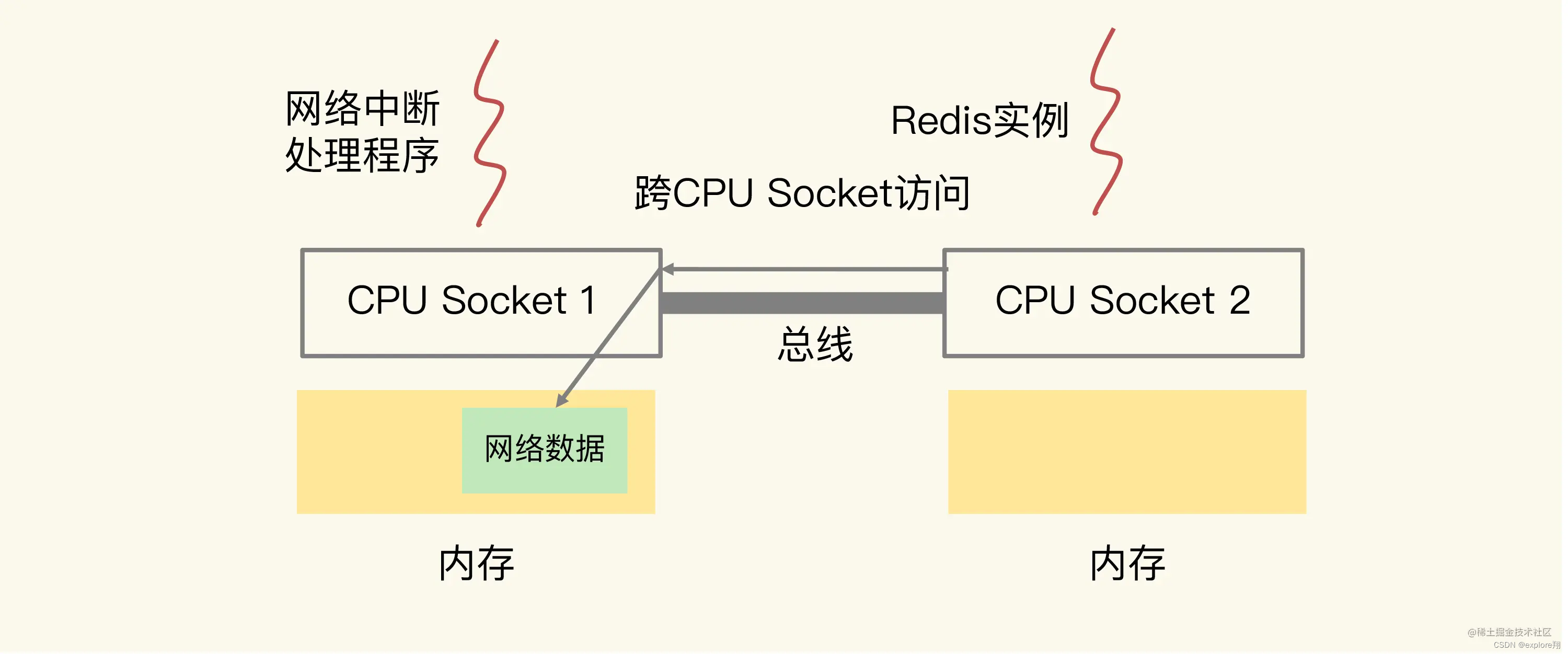
首先，假设我们已经有了一个局部波动率函数，我们在此基础上建立一个二项式局部波动率模型

二项局部波动率模型

假设风险中性条件成立，股票价格 $S(t)$ 的变动服从下面的等式：
$$\frac{dS}{S}=(r-b)dt+\sigma (S,t)dZ$$
其中 $r,b,dZ,\sigma (S,t)$ 分别表示无风险利率、股票的连续股息率、标准维纳过程、局部波动率。在任意时点 $t$，股价变动的方差都满足：
$$(dS{)}^2=S^2{\sigma }^2(S,t)dt$$
一个瞬时时间段 $dt$ 之后，$S$ 的预期价值等于：
$$F=S{e}^{(r-b)dt}$$
也即股票的远期价格

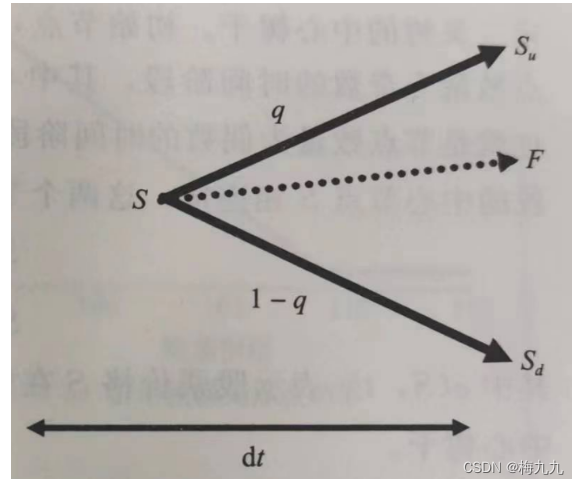
在上述近似二叉树模型中，远期价格就等于 $q$ 测度下，两种股票价格 $S_u,S_d$ 按照概率加权后的平均值，即：
$$F=q{S}_u+(1-q)S_d$$
求解 $q$：
$$q=\frac{F-S_d}{S_u-S_d}$$
$S$ 变动值的方差为：
$$Var[dS]=q(S_u-F{)}^2+(1-q)(S_d-F{)}^2$$
当 $dt\to 0$ 时，$(dS{)}^2=S^2{\sigma }^2(S,t)dt$ 与上式相等，可以得到：
$$S^2{\sigma }^2(S,t)dt=q(S_u-F{)}^2+(1-q)(S_d-F{)}^2$$
将 $q$ 的解析式代入得：
$$\begin{gathered} S^2{\sigma }^2(S,t)dt=\frac{F-S_d}{S_u-S_d}(S_u-F{)}^2+(1-\frac{F-S_d}{S_u-S_d})(S_d-F{)}^2 \\ {S}^2{\sigma }^2(S,t)dt=\frac{F-S_d}{S_u-S_d}(S_u-F{)}^2+(\frac{S_u-F}{S_u-S_d})(S_d-F{)}^2 \\ {S}^2{\sigma }^2(S,t)dt=\frac{(F-S_d)(S_u-F)(S_u-F-S_d+F)}{S_u-S_d}=(F-S_d)(S_u-F) \end{gathered}$$
可以得到每个节点 $S$ 对应得上行股价和下行股价：
$$\begin{gathered} S_u=F+\frac{S^2{\sigma }^2(S,t)dt}{F-S_d} \\ {S}_d=F-\frac{S^2{\sigma }^2(S,t)dt}{S_u-F} \end{gathered}$$
只要知道了 $S,F,S_d$，根据波动率 $\sigma (S,t)$，就可以计算得到 $S_u$；同理，知道了 $S,F,S_u$，就可以计算得到 $S_d$

为了增加时间间隔阶段，我们首先需要确定二叉树的中心，接着按照上述所描述的局部波动率曲面，搭建股价上行和下行的树杈。这样就可以得到一个满足所有局部波动率的二叉树。然后，再利用：
$$q=\frac{F-S_d}{S_u-S_d}$$
回过头来计算每个节点的风险中性概率。做完这以后，我们就可以用逆向归纳法，沿着二叉树倒推出任何股票衍生品的价格

首先，用上一章中描述的 Cox-Ross-Rubinstein (CRR) 方法来确定二叉树的中心树干。初始节点，也就是树根部位的股票价格为 $S_0$，每一个节点数量为奇数的时间阶段，其中心节点 $S$ 都等于初始价格 $S_0$。其他时间阶段，也就是节点数量为偶数的时间阶段，分布于中心两侧最近的两个节点都与上一阶段的中心节点 $S$ 相连接，这两个节点的价格可以表示为
$$\begin{gathered} S_u=S{e}^{\sigma (S,t)\sqrt{dt}} \\ {S}_d=S{e}^{-\sigma (S,t)\sqrt{dt}} \end{gathered}$$
其中 $\sigma (S,t)$ 表示股票价格 $S$ 在未来时间 $t$ 的局部波动率。这种方法明确定义了中心树干。

在每个阶段，从中心节点出发，可以用之前推导出的下式求得上行节点与下行节点：
$$\begin{gathered} S_u=F+\frac{S^2{\sigma }^2(S,t)dt}{F-S_d} \\ {S}_d=F-\frac{S^2{\sigma }^2(S,t)dt}{S_u-F} \end{gathered}$$
在二叉树中，对于中心树干的初始价格 $S_0$ 没有明确的要求。比如，我们可以将股票在每个阶段的远期价格确定为中心价格，也可以选择任何其他价格水平。假设在某一阶段，有奇数个节点，股票的远期价格为 $F_t$，下一个时间阶段就会有偶数个节点，那么 $S_u,S_d$ 就可以改写为：
$$\begin{gathered} S_u=F_t{e}^{\sigma (F_t,t)\sqrt{dt}} \\ {S}_d=F_t{e}^{-\sigma (F_t,t)\sqrt{dt}} \end{gathered}$$
即确保了在 $F_t$ 价格下，局部波动率等于 $\sigma (F_t,t)$

案例：

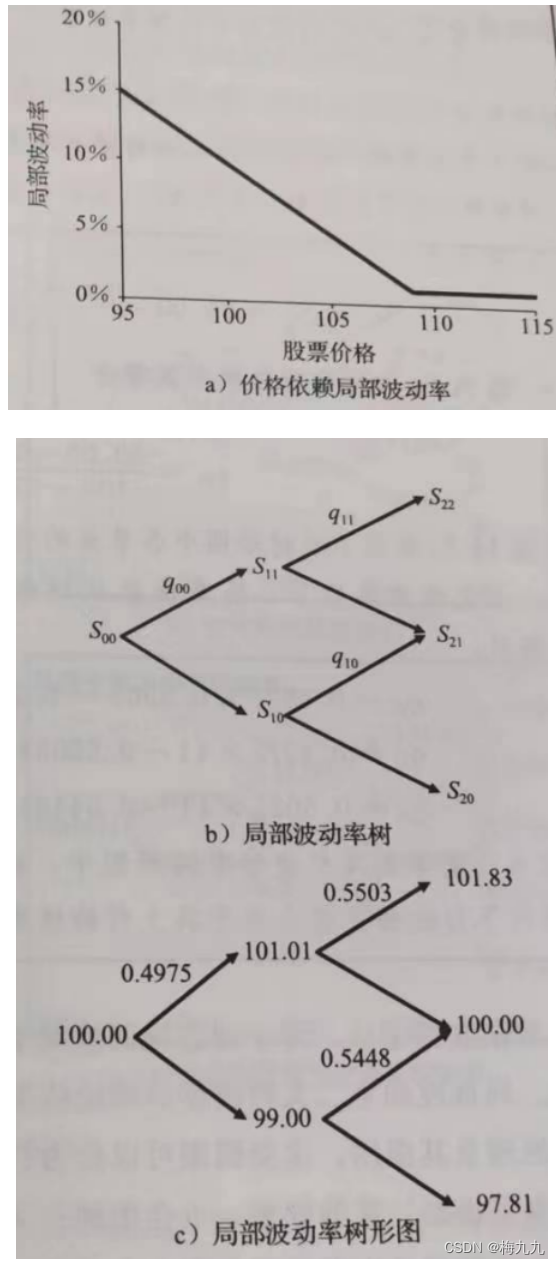
假设某股票当前的价格为 $S_0=100$ 美元。假设局部波动率跟未来的时间 $t$ 没有关系，只会随着股票价格的变动而变动，二者关系如下：
$$\sigma (S)=\max [0.1-\frac{S-S_0}{S_0},0.01]$$
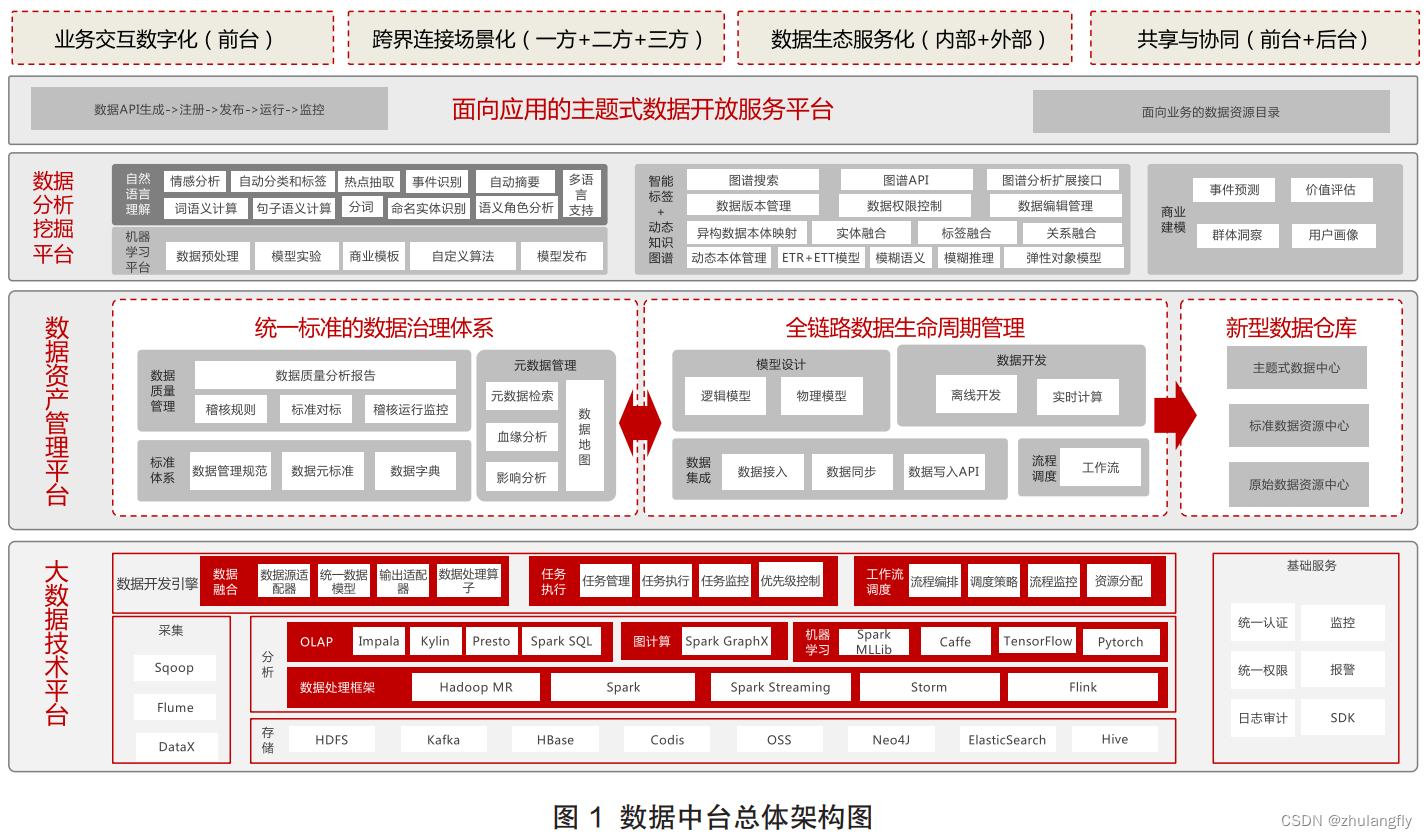
在当前股票价格水平附近，股票价格每升高 1%，局部波动率就会降低1个百分点。为了保证波动率是正数，我们设定波动率最低等于1%。假设股息率和无风险利率都等于 0。令 $\Delta t=0.01$，建立前三个时间间隔阶段的二叉树模型：

利用标准Cox-Ross-Rubinstein模型可得：
$$\begin{gathered} S_{11}=S{e}^{\sigma (S,t)\sqrt{\Delta t}}=100e^{0.1\sqrt{0.01}}=101.01 \\ {S}_{10}=S{e}^{-\sigma (S,t)\sqrt{\Delta t}}=100e^{-0.1\sqrt{0.01}}=99.00 \end{gathered}$$
由于股息率和无风险利率等于0，节点 $S_{00}$ 的远期价格等于初始价格100美元，股价上行的风险中性概率就等于：
$$q_{00}=\frac{F-S_d}{S_u-S_d}=\frac{100.00-99.00}{101.01-99.00}=0.4975$$
令第三阶段的中心节点 $S_{21}$ 的价格等于初始价格100美元

在节点 $S_{11}$ ，局部波动率=0.09，远期价格 $F=S_{11}=101.01$，对应下行节点是 $S_{21}$，对应上行节点是 $S_{22}$，我们有：
$$\begin{gathered} S_{22}=F+\frac{S_{11}^2{\sigma }^2(S_{11},t)\Delta t}{F-S_{21}}=101.01+\frac{101.01^2\times 0.09^2\times 0.01}{101.01-100}=101.83 \\ {q}_{11}=\frac{F-S_{21}}{S_{22}-S_{21}}=\frac{101.01-100}{101.83-100}=0.5503 \end{gathered}$$
类似的，在节点 $S_{10}$ ，局部波动率=0.11，远期价格 $F=S_{10}=99.00$，对应下行节点是 $S_{20}$，对应上行节点是 $S_{21}$​，我们有：
$$\begin{gathered} S_{20}=F-\frac{S_{10}^2{\sigma }^2(S_{10},t)\Delta t}{S_{21}-F}=99.00-\frac{99.00^2\times 0.11^2\times 0.01}{100-99.00}=97.81 \\ {q}_{10}=\frac{F-S_{20}}{S_{21}-S_{20}}=\frac{99.00-97.81}{100-97.81}=0.5448 \end{gathered}$$
在这个简单的局部波动率树形图中，由于波动率会随着股价的下降而上升，股价下行的幅度就会高于其上行的幅度，因此最终的股价呈现负斜度。

局部波动率与隐含波动率的关系

上述展示了如何建立一个局部波动率树形图。现在需要找到一类局部波动率模型，使其可以用来描述观察到的某特定隐含波动率微笑曲线。

假设继续用上个案例中的二叉树模型，局部波动率函数保持不变，将其扩展到五个时间间隔阶段，得到如下五阶段局部波动率模型二叉树模型

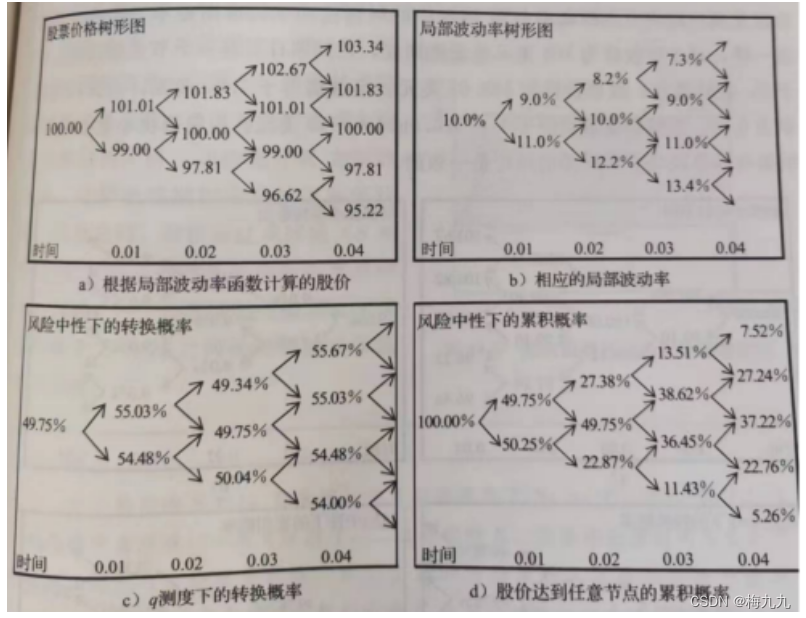
假设有一个欧式看涨期权，行权价为102美元，到期日为5个时间阶段，根据树形图的最终节点，唯一一个在到期日处于实值状态的期权对应的股票价格是103.34美元，此时期权对应的价格是1.34美元。在风险中性条件下，假设无风险利率等于0，那么该期权的现值就是1.34美元。该期权的风险中性预期价值就等于其现值乘以股价到达该节点的累积概率7.52%，即 $1.34\times 0.0752=0.10$ 美元。由于该看涨期权在其他任何一个节点的价值都等于0，因此，0.10美元就是期权在初始时的价值。

另一个角度考虑，股价在到期日高于102美元的风险中性概率又取决于股票在到期日等于实值状态价格之前，股价落在100美元和102美元之间的平均局部波动率水平

根据局部波动率函数，股价在100美元和102美元之间对应的平均局部波动率等于 $(10\%+8\%)/2=9\%$。可以猜测，在动态局部波动率模型中，行权价为102美元的看涨期权价格，就等于波动率为9%的常数波动率二叉树模型中的价格

为了验证该猜测是否正确，根据CRR方法，建立一个波动率为9%的常数波动率二叉树模型：

对于行权价为102美元的看涨期权，在到期日只有一个节点的损益不等于0，在该节点，股票价格为103.67美元。损益值等于1.67美元，当无风险利率为0时，期权的现值就等于 $1.67\times 0.0614=0.10$ 美元，保留两位小数点之后，结果与局部波动率树形图的结论是一致的。

在常数波动率二叉树模型中，取极限条件，时间间隔趋近于无穷小时，得到的期权价值会收敛至BSM公式的结果

上述案例中，在期权估值时用到的CRR隐含波动率，约等于当前股价水平和期权行权价水平对应的两个局部波动率的线性平均值。对应地，在连续极限条件下，我们推测，正确的BSM隐含波动率约等于股票价格和行权价的两个局部波动率的平均值

为什么这一关系成立？下图展示了不同的股价变动路径。要使最后期权的损益为正数，股价路径就必须上穿过初始股票价格 $S$ 和行权价 $K$ 之间的区域，这样最终期权才能处于实值状态。在此之前，股价穿过该区域，对应的就是局部波动率的样本。因此，一个标准期权的隐含波动率就约等于 $S$ 与 $K$ 之间的局部波动率线性平均值

两倍定律：理解局部波动率和隐含波动率之间的关系

期权的隐含波动率 $\Sigma (S，K)$ 约等于局部波动率 $\sigma (S)$ 的平均值，这是指在期权有效期内，股价位于当前标的资产价格和行权价之间时的局部波动率。这种关系类似于零息债券，其到期收益率等于远期利率平均值

对于利率而言，正是由于存在这种关系，短端利率的远期值随时间增长的速率是到期收益率增长速率的两倍。与此类似，如果局部波动率函数 $\sigma (S)$ 只受股价这一个变量的影响，那么我们也可以证明，局部波动率随股票价格变动的速率约等于隐含波动率随行权价格变动速率的两倍。通常，我们将这种关系称为两倍定律。

一个非正式证明：假设一个指数的局部波动率与时间无关，仅与指数价格保持线性关系，于是有：
$$\sigma (S)={\sigma }_0+\beta S$$
假设有一个处于浅度虚值状态的看涨期权，行权价为 $K$，标的指数的价格水平是 $S$，其隐含波动率表示为 $\Sigma (S,K)$。影响期权价值的每一条股价变动路径都将穿过 $S$ 和 $K$ 之间的区域，如下图所示。这些路径对应的波动率主要是由 $S$ 和 $K$ 之间的局部波动率决定的。因此，该期权的隐含波动率可以看作等于行权价 $K$ 和指数价格水平 $S$ 之间的平均局部波动率，也就是图中的阴影部分：

于是：
$$\begin{gathered} \Sigma (S,K)\approx \frac{1}{K-S}{\int }_S^K\sigma (S^{\prime })d{S}^{\prime } \\ \Sigma (S,K)\approx \frac{1}{K-S}{\int }_S^K({\sigma }_0+\beta S^{\prime })d{S}^{\prime } \\ =\frac{1}{K-S}({\sigma }_0{S}^{\prime }+\frac{1}{2}\beta S^{\prime 2}){|}_S^K \\ =\frac{1}{K-S}[{\sigma }_0(K-S)+\frac{1}{2}\beta (K^2-S^2)] \\ ={\sigma }_0+\frac{\beta }{2}(K+S) \end{gathered}$$
比较 $\sigma (S)={\sigma }_0+\beta S$ 与 $\Sigma (S,K)\approx {\sigma }_0+\frac{\beta }{2}(K+S)$，可以看出，局部波动率随 $S$ 变动的速率是隐含波动率随 $S$ 变动速率的两倍，同时隐含波动率随 $S$ 变动的速率等于其随 $K$ 变动的速率

将两式结合可更直观地得到隐含波动率和局部波动率之间的关系：
$$\Sigma (S,K)\approx \sigma (S)+\frac{\beta }{2}(K-S)$$