字典树（Trie）

一、问题引入

现有长度为n的字符串数组，[“go”，“goog”，“google”，“golang”，“baidu”，“leetCode”，“good”]，给你一个字符串前缀如“go”，你需要从字符串中查找出所有以“go”为前缀的所有字符串
1、向数组中插入一个新的字符串
2、从字符串数组中查找出所有以“go”为前缀的字符字符串的个数

插入

插入操作比较简单，我们知道数组长度为n，那么可以直接插入，时间复杂度为O(1)

查询

最简单并且最容易想到的方法就是暴力求解，那他的时间复杂度是多少? 字符串数组的长度为n，字符串前缀的长度为k，那我们需要遍历数组中每一个字符串，并且对这些字符串的前k个字符进行判断，那么暴力求解的时间复杂度就是O(kn)

那有没有更加快速的方法呢?

我们想一下，查询的这个操作是否跟我们查询字典的操作有些类似的，如果你要查找以“go”为前缀的单词，是不是需要先找到首字母“g”的部分？然后在查找第二个字母“o”，那我们能不能自己也建一部字典，实现上述的查询和插入问题呢？

二、字典树介绍

字典树，英文名 trie。顾名思义，就是一个像字典一样的树。

我们怎么用树来存储上述字符串数组呢？
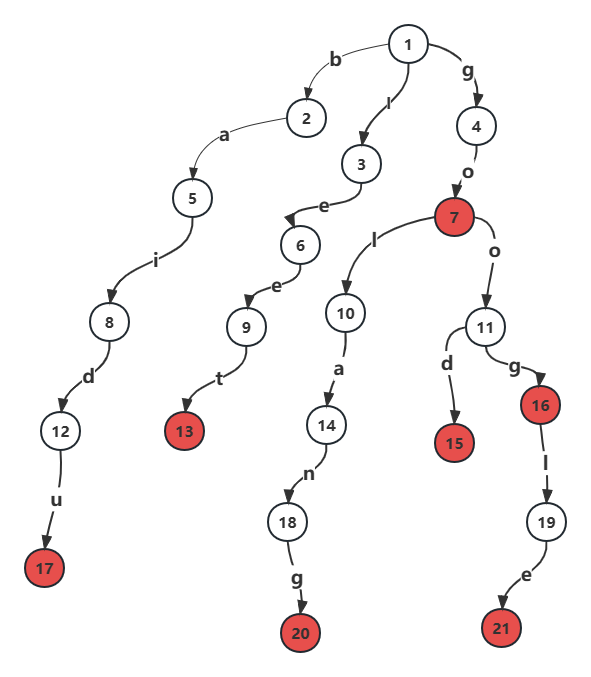
在这里插入图片描述
可以发现，这棵字典树用边来代表字母，而从根结点到树上某一结点的路径就代表了一个字符串。举个例子，1->4->7->15 表示的就是字符串 good。

3、字典树的实现

如题中所述，数组中字符串由小写字母构成，因此我们可将将字典树看成一个26叉树（小写字母有26个）。假设数组中字符串的总长度为N，那么最坏情况下，字典树存在N+1个节点（根节点不存字符，最坏情况下数组中所有字符串没有相同的前缀，因此每个字符串都单独构成一条路径）
因此我们可以设一个二维数组son来存储Trie

son[N+10][26]

我们如何理解son中的元素呢？
对于son[x][y]

x:上方节点的编号
y:边上的值
son[x][y]：下方节点的编号

因为数组下标只能是整数，我们把a~z转化成0 ~ 26。

现规定从0开始对节点逐个编号，编号为0的节点是根节点（Trie为空时仅含根节点），同时 son 数组进行全0初始化。我们来看如何将字符c插入到Trie中。

如果 son[0][c] == 0 成立，说明Trie中不含字符c，此时应当令 son[0][c] = idx，其中 idx 为新建立的节点的编号。否则,c 已存在于Trie中，无需插入。

4、存储与查询

我们需要用son来存储Trie，还需要用idx来为每个节点编号，但是我们怎么知道存储的哪些字符串呢？
考虑上面所说的“goo”,“google”
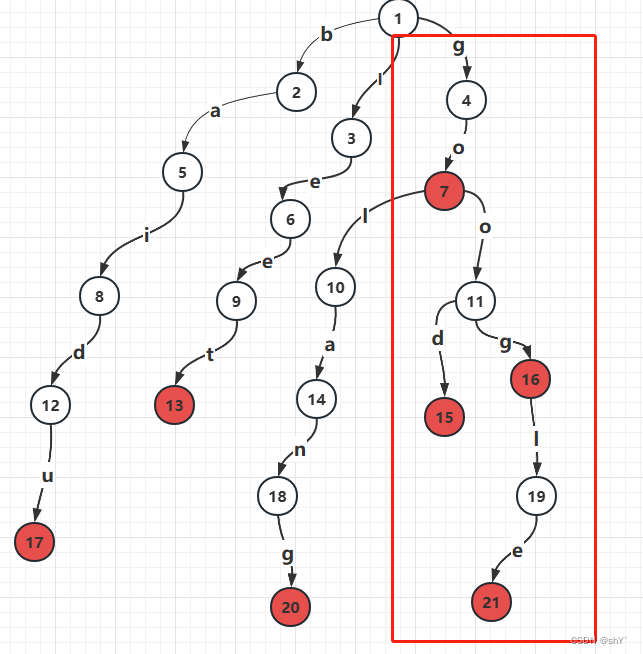
在这里插入图片描述
我们需要一个数组cnt[]来存储以某个节点为结尾的字符串的个数，如果一个字符串的结尾节点标号为p，我们只需要cnt[p]++

此时，我们已经介绍了字典树需要的所有变量

static final int N = 100010;
static int[][] son = new int[N][26];
static int[] cnt = new int[N];
static int idx;

存储一个字符串的实现如下：

//s代表所有存储的字符串，length代表s的长度
public static void insert(String s,int length)
    {
        char[] sc = s.toCharArray();
        int p = 0;
        for(int i = 0; i < length; i++)
        {
            int u = sc[i] - 'a';//将字符转换成序号
            if(son[p][u] == 0) son[p][u] = ++idx;//如果节点不存在则新建节点
            p = son[p][u];//如果节点存在则向下传递
        }
        cnt[p]++;//字符串遍历结束，将尾结点+1
    }

查询字符串与实现操作类似

public static int query(String s, int length)
    {
        char[] sc = s.toCharArray();
        int p = 0;
        for(int i = 0; i <length; i++)
        {
            int u = sc[i] - 'a';
            if(son[p][u] == 0) return 0;//如果节点不存在，返回0
            p = son[p][u];//如果节点存在，向下传递
        }
        return cnt[p];//返回结果
    }