【数据结构入门】-链表之双向循环链表

news2024/10/5 14:08:18

个人主页：平行线也会相交
欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 平行线也会相交 原创
收录于专栏【数据结构初阶（C实现）】
在这里插入图片描述

文章目录

  • 链表初始化
  • 打印链表
  • 尾插
  • 尾删
  • 新建一个节点
  • 头插
  • 头删
  • 查找
  • 在pos之前插入*
  • 删除pos位置
  • 销毁链表
  • 总代码
    • test.c
    • List.h
    • List.c

链表初始化

LTNode* ListInit(LTNode* phead)
{
	//哨兵位头节点
	phead = (LTNode*)malloc(sizeof(LTNode));
	phead->next = phead;
	phead->prev = phead;

	return phead;
	//利用返回值的方式
}

首先，我们需要一个哨兵头节点，该头节点的next和prev均指向该头节点本身，最后，返回这个头节点的地址。

打印链表

void ListPrint(LTNode* phead)
{
	assert(phead);
	LTNode* cur = phead->next;//从phead->开始遍历链表

	while (cur != phead)//为了防止死循环，所以终止条件为cur=phead
	{
		printf("%d ", cur->data);
		cur = cur->next;
	}
	printf("\n");
}

由于链表是双向循环链表，双向循环链表自身的结构很容易在打印时造成死循环，所以我们在打印链表时需要注意循环终止的条件，否则，程序就会陷入死循环。再次提醒，这是一个双向循环链表。当我们循环打印完链表的最后一个数据的时候，此时cur就是指向链表中最后一个节点的，而cur->next是指向链表的哨兵头节点的，所以，循环终止条件就是cur=phead。

尾插

void ListPushBack(LTNode* phead, LTDateType x)
{
	//链表为空时，依然可以处理
	assert(phead);
	LTNode* tail = phead->prev;//找到尾节点
	LTNode* newnode = (LTNode*)malloc(sizeof(LTNode));
	newnode->data = x;

	//phead
	tail->next = newnode;
	newnode->prev = tail;
	newnode->next = phead;
	phead->prev = newnode;
}

尾删

//尾删
void ListPopBack(LTNode* phead)
{
	assert(phead);
	assert(phead->next != phead);//当链表为空时，就表示不能再删除了

	//找到尾
	LTNode* tail = phead->prev;
	phead->prev = tail->prev;
	tail->prev->next = phead;

	//最后释放空间
	free(tail);
}

既然是尾删，我们首先要先找到尾，即LTNode* tail = phead->prev;这样会方便很多，同时尾删的时候一定要注意**free（）**的释放时机。
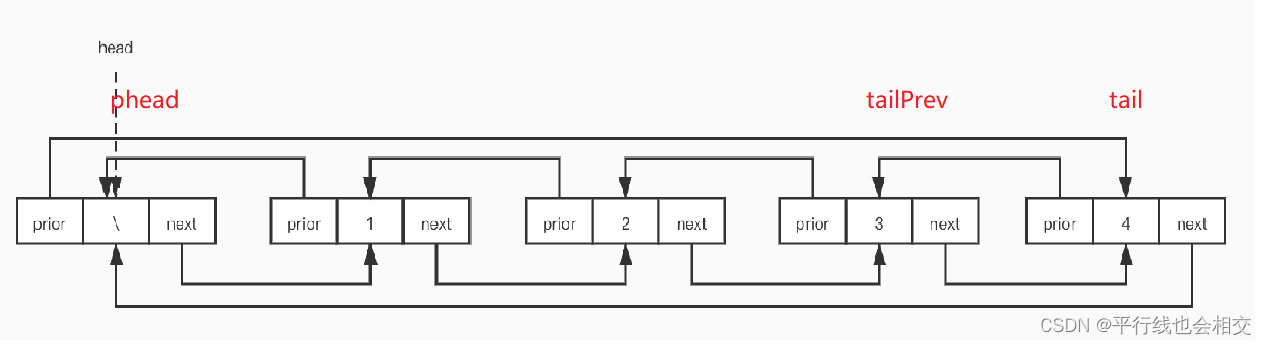
在这里插入图片描述
注意一种特殊情况：当phead->next==phead的时候，此时链表为空，就不能继续删除了。所以需要加上 assert(phead->next != phead);。
在这里插入图片描述

新建一个节点

LTNode* BuyListNode(LTDateType x)
{
	LTNode* newnode = (LTNode*)malloc(sizeof(LTNode));
	newnode->data = x;
	newnode->prev = NULL;
	newnode->next = NULL;
	return newnode;
}

该函数功能就是新建一个节点，把该节点的数据进行赋值（即newnode->data = x;），并把指针均变成空指针（newnode->prev = NULL; newnode->next = NULL;）。最后返回这个新节点的地址即可。

头插

void ListPushFront(LTNode* phead, LTDateType x)
{
	assert(phead);
	LTNode* newnode = BuyListNode(x);
	LTNode* next = phead->next;

	phead->next = newnode;
	newnode->prev = phead;
	newnode->next = next;
	next->prev = newnode;
}

还是看一下特殊情况，即如果链表是一个空链表，我们来简单分析一下：链表为空时phead->next就是phead本身。
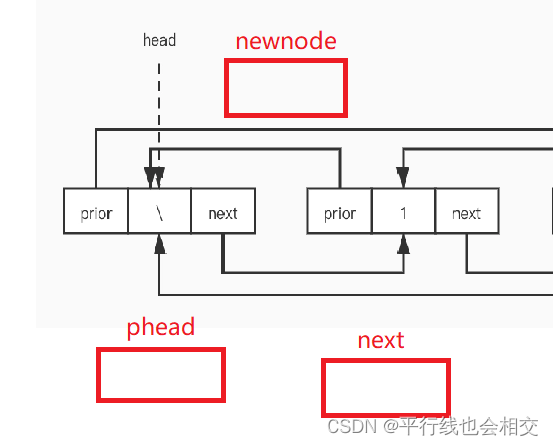
在这里插入图片描述
我们只需要处理phead、next、newnode三者之间的链接关系即可。最后发现，链表为空时依然可以进行处理。

头删

void ListPopFront(LTNode* phead)
{
	assert(phead);
	//链表为空就不需要头删了
	LTNode* next = phead->next;
	LTNode* nextNext = next->next;

	phead->next = nextNext;
	nextNext->prev = phead;

	free(next);
}

链表为空时就不要进行头删操作了，故加上assert(phead);我们最好还是提前定义好next和nextNext即LTNode* next = phead->next;
LTNode* nextNext = next->next;
这样后面会很方便，可以减少不必要的麻烦，接下来处理phead、next、nextNext三者之间的链接关系就好了。

查找

查找的实现与打印的实现差不太多，提前定义一个cur指向phead的next，即LTNode* next = phead->next;循环终止条件依然是cur = phead，其它按部就班即可。

LTNode* ListFind(LTNode* phead, LTDateType x)
{
	assert(phead);
	LTNode* cur = phead->next;

	while (cur != phead)
	{
		if (cur->data == x)
		{
			return cur;
		}
		cur = cur->next;
	}
	//没找到就返回NULL
	return NULL;
}

在pos之前插入*

void ListInsert(LTNode* pos, LTDateType x)
{
	assert(pos);
	LTNode* posPrev = pos->prev;
	LTNode* newnode = BuyListNode(x);

	//处理posPrev  newnode  pos三者之间的链接关系
	posPrev->next = newnode;
	newnode->prev = posPrev;

	newnode->next = pos;
	pos->prev = newnode;
}

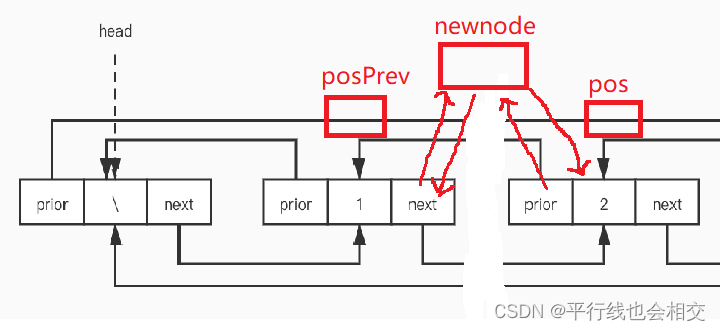
在这里插入图片描述
一定要提前定义一个posPrev即LTNode* posPrev = pos->prev;，然后进行newnode、pos、posPrev之间的链接就好。
在这里，我们还可以利用ListInsert这个函数来完成头插尾插的操作。
首先，我们先利用ListInsert来完成尾插的操作。
当pos是我们的哨兵位节点phead的时候，由于这个函数是在pos之前插入，所以此时就相当于尾插了（因为phead->prev就是尾）。

void ListPushBack(LTNode* phead, LTDateType x)
{
	//链表为空时，依然可以处理
	assert(phead);
	//LTNode* tail = phead->prev;//找到尾节点
	//LTNode* newnode = (LTNode*)malloc(sizeof(LTNode));
	//newnode->data = x;

	phead
	//tail->next = newnode;
	//newnode->prev = tail;
	//newnode->next = phead;
	//phead->prev = newnode;

	ListInsert(phead, x);
}

现在再来看头插：
当phead->next和pos相等时，此时就相当于头插。

void ListPushFront(LTNode* phead, LTDateType x)
{
	assert(phead);
	//LTNode* newnode = BuyListNode(x);
	//LTNode* next = phead->next;

	//phead->next = newnode;
	//newnode->prev = phead;
	//newnode->next = next;
	//next->prev = newnode;
	ListInsert(phead->next, x);
}

所以我们以后想要快速的写双向循环链表的时候，头插、尾插、或者任意位置的插入都可以利用ListInsert这个函数来快速的实现双向循环链表。把phead->prev传给pos就是尾插，把phead->next传给pos就变成了头删。所以双向链表只需要实现两个函数（ListInsert和ListErase）就都搞定了，这也是双向链表结构的一个优势。

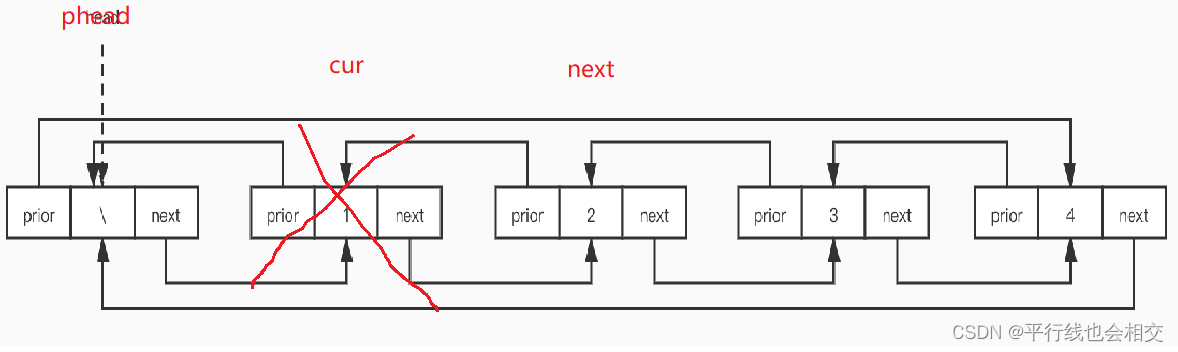
删除pos位置

void ListErase(LTNode* pos)
{
	assert(pos);
	LTNode* posPrev = pos->prev;
	LTNode* posNext = pos->next;

	posPrev->next = posNext;
	posNext->prev = posPrev;
	free(pos);
}

一般来说，我们想要删除某个数据先是调用ListFind来返回一个地址，然后才调用ListErase继而把该数据删除，请看：

void TestList2()
{
	LTNode* plist = NULL;
	plist = ListInit(plist);

	ListPushFront(plist, 1);
	ListPushFront(plist, 2);
	ListPushFront(plist, 3);
	ListPushFront(plist, 4);
	ListPrint(plist);

	ListPushBack(plist, 1);
	ListPushBack(plist, 2);
	ListPushBack(plist, 3);
	ListPushBack(plist, 4);
	ListPrint(plist);

	LTNode* pos = ListFind(plist, 2);
	if (pos != NULL)
	{
		ListErase(pos);
	}
	ListPrint(plist);
}

在这里插入图片描述
我们可以看到运行结果成功把第一个2删除了。
然而ListErase的功能不仅仅只有这些，我们还可以利用ListErase来完成头删尾删的操作。

请看：

//尾删
void ListPopBack(LTNode* phead)
{
	assert(phead);
	assert(phead->next != phead);//当链表为空时，就表示不能再删除了

	找到尾
	//LTNode* tail = phead->prev;
	//phead->prev = tail->prev;
	//tail->prev->next = phead;

	最后释放空间
	//free(tail);
	ListErase(phead->prev);
}

//头删
void ListPopFront(LTNode* phead)
{
	assert(phead);
	链表为空就不需要头删了
	//LTNode* next = phead->next;
	//LTNode* nextNext = next->next;

	//phead->next = nextNext;
	//nextNext->prev = phead;

	//free(next);
	ListErase(phead->next);
}

现在我们来测试一下：

void TestList2()
{
	LTNode* plist = NULL;
	plist = ListInit(plist);

	ListPushFront(plist, 1);
	ListPushFront(plist, 2);
	ListPushFront(plist, 3);
	ListPushFront(plist, 4);
	ListPrint(plist);

	ListPushBack(plist, 1);
	ListPushBack(plist, 2);
	ListPushBack(plist, 3);
	ListPushBack(plist, 4);
	ListPrint(plist);

	LTNode* pos = ListFind(plist, 2);
	if (pos != NULL)
	{
		ListErase(pos);
	}
	ListPrint(plist);

	ListPopBack(plist);
	ListPopBack(plist);
	ListPopFront(plist);
	ListPopFront(plist);
	ListPrint(plist);
}

在这里插入图片描述

销毁链表

最后，我们再来实现一下销毁链表。

//销毁链表
void ListDestroy(LTNode* phead)
{
	assert(phead);
	LTNode* cur = phead->next;
	while (cur != phead)
	{
		LTNode* next = cur->next;
		free(cur);
		cur = next;
	}
	free(phead);
	//想要把phead置为空，需要再函数外部进行置空，当然如果传二级指针也可以在函数内部把
	//phead置为空，不过因为我们这个双向链表都是传的一级指针，所以为了保持接口一致性，
	//我们在函数外部把phead置为空即可
}

在这里插入图片描述

以上就是双向循环链表所以接口函数的实现。

总代码

test.c

#include"List.h"

void TestList1()
{
	LTNode* plist = NULL;//初始化
	plist = ListInit(plist);
	ListPushBack(plist, 1);
	ListPushBack(plist, 2);
	ListPushBack(plist, 3);
	ListPushBack(plist, 4);
	ListPrint(plist);

	ListPushFront(plist, 1);
	ListPushFront(plist, 2);
	ListPushFront(plist, 3);
	ListPushFront(plist, 4);
	ListPrint(plist);
}

void TestList2()
{
	LTNode* plist = NULL;
	plist = ListInit(plist);

	ListPushFront(plist, 1);
	ListPushFront(plist, 2);
	ListPushFront(plist, 3);
	ListPushFront(plist, 4);
	ListPrint(plist);

	ListPushBack(plist, 1);
	ListPushBack(plist, 2);
	ListPushBack(plist, 3);
	ListPushBack(plist, 4);
	ListPrint(plist);

	LTNode* pos = ListFind(plist, 2);
	if (pos != NULL)
	{
		ListErase(pos);
	}
	ListPrint(plist);

	ListPopBack(plist);
	ListPopBack(plist);
	ListPopFront(plist);
	ListPopFront(plist);
	ListPrint(plist);

	ListDestroy(plist);
	plist = NULL;
}

int main()
{
	//TestList1();
	TestList2();
	return 0;
}

List.h

#pragma once

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>

typedef int LTDateType;

typedef struct ListNode
{
	LTDateType data;
	struct ListNode* next;
	struct ListNode* prev;
}LTNode;


LTNode* ListInit(LTNode* phead);//初始化
void ListPrint(LTNode* phead);  //打印链表

//尾插
void ListPushBack(LTNode* phead, LTDateType x);

//尾删
void ListPopBack(LTNode* phead);

//头插
void ListPushFront(LTNode* phead, LTDateType x);

//头删
void ListPopFront(LTNode* phead);

//创建新节点
LTNode* BuyListNode(LTDateType x);

//查找
LTNode* ListFind(LTNode* phead, LTDateType x);

//pos位置之前插入
void ListInsert(LTNode* pos, LTDateType x);

//删除pos位置
void ListErase(LTNode* pos);

//销毁聊表
void ListDestroy(LTNode* phead);

List.c

#include"List.h"


//初始化
LTNode* ListInit(LTNode* phead)
{
	//哨兵位头节点
	phead = (LTNode*)malloc(sizeof(LTNode));
	phead->next = phead;
	phead->prev = phead;

	return phead;
	//利用返回值的方式
}

void ListPushBack(LTNode* phead, LTDateType x)
{
	//链表为空时，依然可以处理
	assert(phead);
	//LTNode* tail = phead->prev;//找到尾节点
	//LTNode* newnode = (LTNode*)malloc(sizeof(LTNode));
	//newnode->data = x;

	phead
	//tail->next = newnode;
	//newnode->prev = tail;
	//newnode->next = phead;
	//phead->prev = newnode;

	ListInsert(phead, x);
}

void ListPrint(LTNode* phead)
{
	assert(phead);
	LTNode* cur = phead->next;//从phead->开始遍历链表

	while (cur != phead)//为了防止死循环，所以终止条件为cur=phead
	{
		printf("%d ", cur->data);
		cur = cur->next;
	}
	printf("\n");
}

//尾删
void ListPopBack(LTNode* phead)
{
	assert(phead);
	assert(phead->next != phead);//当链表为空时，就表示不能再删除了

	找到尾
	//LTNode* tail = phead->prev;
	//phead->prev = tail->prev;
	//tail->prev->next = phead;

	最后释放空间
	//free(tail);
	ListErase(phead->prev);
}

LTNode* BuyListNode(LTDateType x)
{
	LTNode* newnode = (LTNode*)malloc(sizeof(LTNode));
	newnode->data = x;
	newnode->prev = NULL;
	newnode->next = NULL;
	return newnode;
}

void ListPushFront(LTNode* phead, LTDateType x)
{
	assert(phead);
	//LTNode* newnode = BuyListNode(x);
	//LTNode* next = phead->next;

	//phead->next = newnode;
	//newnode->prev = phead;
	//newnode->next = next;
	//next->prev = newnode;
	ListInsert(phead->next, x);
}

//头删
void ListPopFront(LTNode* phead)
{
	assert(phead);
	链表为空就不需要头删了
	//LTNode* next = phead->next;
	//LTNode* nextNext = next->next;

	//phead->next = nextNext;
	//nextNext->prev = phead;

	//free(next);
	ListErase(phead->next);
}

//查找
LTNode* ListFind(LTNode* phead, LTDateType x)
{
	assert(phead);
	LTNode* cur = phead->next;

	while (cur != phead)
	{
		if (cur->data == x)
		{
			return cur;
		}
		cur = cur->next;
	}
	//没找到就返回NULL
	return NULL;
}

//pos位置之前插入
void ListInsert(LTNode* pos, LTDateType x)
{
	assert(pos);
	LTNode* posPrev = pos->prev;
	LTNode* newnode = BuyListNode(x);

	//处理posPrev  newnode  pos三者之间的链接关系
	posPrev->next = newnode;
	newnode->prev = posPrev;

	newnode->next = pos;
	pos->prev = newnode;
}

//删除pos位置
void ListErase(LTNode* pos)
{
	assert(pos);
	LTNode* posPrev = pos->prev;
	LTNode* posNext = pos->next;

	posPrev->next = posNext;
	posNext->prev = posPrev;
	free(pos);
}

//销毁链表
void ListDestroy(LTNode* phead)
{
	assert(phead);
	LTNode* cur = phead->next;
	while (cur != phead)
	{
		LTNode* next = cur->next;
		free(cur);
		cur = next;
	}
	free(phead);
	//想要把phead置为空，需要再函数外部进行置空，当然如果传二级指针也可以在函数内部把
	//phead置为空，不过因为我们这个双向链表都是传的一级指针，所以为了保持接口一致性，
	//我们在函数外部把phead置为空即可
}

好了，双向循环链表的实现就到这里了，其实在这里面最重要的两个接口函数就是ListErase和ListInser，这两个函数可以帮助我们快速的实现这个链表，剩余的就是一些边边角角的问题了。
这块的内容还是要多画图，来帮助我们更好的理解。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/393897.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

CSS中的伪元素和伪类

CSS中的伪元素和伪类

一直被伪类和伪元素所迷惑&#xff0c;以为是同一个属性名称&#xff0c;根据CSS动画&#xff0c;索性开始研究a:hover:after&#xff0c;a.hover:after的用法。 伪元素 是HTML中并不存在的元素&#xff0c;用于将特殊的效果添加到某些选择器。 对伪元素的描述 伪元素有两…
阅读更多...
【Verilog】握手信号实现跨时钟域数据传输-handshake

【Verilog】握手信号实现跨时钟域数据传输-handshake

文章目录handshake握手电路使用握手信号实现跨时钟域数据传输接口信号图题目描述解题思路代码设计数据发送模块data_driver数据接收模块data_receivertestbench波形handshake握手电路 跨时钟域处理是个很庞大并且在设计中很常出现的问题握手(handshake)是用来处理信号跨时钟域…
阅读更多...
数字化引领乡村振兴，VR全景助力数字乡村建设

数字化引领乡村振兴，VR全景助力数字乡村建设

一、数字乡村建设加速经济发展随着数字化建设的推进&#xff0c;数字化农业产业正在成为农业产业发展的主导力量&#xff0c;因此数字化技术赋予农业产业竞争力的能力不可小觑。数字化乡村建设背景下&#xff0c;数字化信息技术将全面改造升级农村产业&#xff0c;从农业、养殖…
阅读更多...
new set数组对象去重失败

new set数组对象去重失败

我们知道Set是JS的一个种新的数据结构&#xff0c;和数组类似&#xff0c;和数组不同的是它可以去重&#xff0c;比如存入两个1或两个"123"&#xff0c;只有1条数据会存入成功&#xff0c;但有个特殊情况&#xff0c;如果添加到set的值是引用类型&#xff0c;比如数组…
阅读更多...
DataGear 4.5.1 发布，数据可视化分析平台

DataGear 4.5.1 发布，数据可视化分析平台

DataGear 4.5.1 发布&#xff0c;严重 BUG 修复&#xff0c;具体更新内容如下&#xff1a; 修复&#xff1a;修复SQL数据集对于DB2、SQLite等数据源预览时会报错的BUG&#xff1b;修复&#xff1a;修复系统对于MySQL、MariaDB等数据源中无符号数值类型有时报错的BUG&#xff1…
阅读更多...
借助媛如意让ROS机器人turtlesim画出美丽的曲线-云课版本

借助媛如意让ROS机器人turtlesim画出美丽的曲线-云课版本

首先安装并打开猿如意其次打开蓝桥云课ROS并加入课程在猿如意输入问题得到答案在蓝桥云课ROS验证如何通过turtlesim入门ROS机器人您可以通过以下步骤入门ROS机器人&#xff1a;安装ROS&#xff1a;您需要安装ROS&#xff0c;可以在ROS官网上找到安装指南。安装turtlesim&#x…
阅读更多...
英文拼写检查：TX Spell .NET for .NET 10.0 Crack

英文拼写检查：TX Spell .NET for .NET 10.0 Crack

用于 Windows 窗体应用程序的 TX Text Control .NET 的强大拼写检查和语言工具。 表现 可靠准确的拼写检查 使用 TX Spell .NET for Windows Forms&#xff0c;您可以为基于 TX Text Control 的应用程序添加极其快速、高度可靠和非常准确的拼写检查。将 TX Spell .NET for Wind…
阅读更多...
mysql中的共享锁，排他锁，间隙锁，意向锁及死锁机制

mysql中的共享锁，排他锁，间隙锁，意向锁及死锁机制

一、前言&#xff08;以下均为读完 高性能Mysql第四版 后的个人理解&#xff0c;建议阅读&#xff0c;挺不错的&#xff09;在写锁机制前先简单贴出mysql InnoDB引擎中的事务特性与隔离级别&#xff1a;事务的ACID标准(1)原子性-atomicity&#xff1a;一个事务作为一个不可分割…
阅读更多...
vue中使用富文本Tinymce

vue中使用富文本Tinymce

本文是直接引用vue-element-admin中的&#xff0c;在此记录方便下次使用&#xff0c;日后再详细注释。 再src下的components下创建Tinymce 下包含以下文件 index.vue是主体文件 plugins.js 是 插件配置 toolbar.js 是 粗体、斜体等配置 EditorImage.vue 是右上角的上传 封装后…
阅读更多...
一文速学-GBDT模型算法原理以及实现+Python项目实战

一文速学-GBDT模型算法原理以及实现+Python项目实战

目录 前言 一、GBDT算法概述 1.决策树 2.Boosting 3.梯度提升 使用梯度上升找到最佳参数 二、GBDT算法原理 1.计算原理 2.预测原理 三、实例算法实现 1.模型训练阶段 1&#xff09;初始化弱学习器 2&#xff09;对于建立M棵分类回归树​&#xff1a; 四、Python实现 …
阅读更多...
Spring_让Spring 依赖注入彻底废掉

Spring_让Spring 依赖注入彻底废掉

在Spring之基于注解方式实例化BeanDefinition&#xff08;1&#xff09;_chen_yao_kerr的博客-CSDN博客中&#xff0c;我们在末尾处分享了一个甜点&#xff0c;就是关于实现了BeanDefinitionRegistryPostProcessor也可以实例化bean的操作&#xff0c;首先需要去了解一下那篇博客…
阅读更多...
宝塔（二）：升级JDK版本

宝塔（二）：升级JDK版本

目录 背景 一、下载JDK17 二、配置环境变量 三、配置新的JDK路径 背景 宝塔的软件商店只有JDK8&#xff0c;不满足我当前项目所需的JDK版本&#xff0c;因此想对JDK版本进行升级&#xff0c;升级为JDK17。 一、下载JDK17 先进入 /usr/lib/jvm 目录 点击终端&#xff0c;进…
阅读更多...
OpenCV——line、circle、rectangle、ellipse、polylines函数的使用和绘制文本putText函数以及绘制中文的方法。

OpenCV——line、circle、rectangle、ellipse、polylines函数的使用和绘制文本putText函数以及绘制中文的方法。

学习OpenCV的过程中&#xff0c;画图是不可避免的&#xff0c;本篇文章旨在介绍OpenCV中与画图相关的基础函数。 1、画线条——line()函数 介绍&#xff1a; cv2.line(image, start_point, end_point, color, thickness)参数&#xff1a; image: 图像start_point&#xff1a…
阅读更多...
拉链表（小记）

拉链表（小记）

拉链表创建外部表将编写的orders.txt上传到hdfs创建一个增减分区表将orders表的数据传入ods_orders_inc查看分区创建历史表插入数据操作创建外部表 create database lalian; use lalian;create external table orders(orderId int,createDate string,modifiedTime string,stat…
阅读更多...
Redis集群方案应该怎么做？

Redis集群方案应该怎么做？

今天我们来跟大家唠一唠JAVA核心技术-RedisRedis是一款流行的内存数据库&#xff0c;适用于高性能的数据缓存和实时数据处理。当需要处理大量数据时&#xff0c;可以使用Redis集群来提高性能和可用性。Redis在单节点模式下&#xff0c;虽然可以支持高并发、快速读写、丰富的数据…
阅读更多...
sizeof与一维数组和二维数组

sizeof与一维数组和二维数组

&#x1f355;博客主页&#xff1a;️自信不孤单 &#x1f36c;文章专栏&#xff1a;C语言 &#x1f35a;代码仓库&#xff1a;破浪晓梦 &#x1f36d;欢迎关注&#xff1a;欢迎大家点赞收藏关注 sizeof与一维数组和二维数组 文章目录sizeof与一维数组和二维数组前言1. sizeof与…
阅读更多...
专业版即将支持自定义场景测试

专业版即将支持自定义场景测试

物联网 MQTT 测试云服务 XMeter Cloud 专业版于 2022 年底上线后&#xff0c;已有不少用户试用&#xff0c;对数千甚至上万规模的 MQTT 并发连接和消息吞吐场景进行测试。同时我们也收到了希望支持更多物联网协议测试的需求反馈。 新年伊始&#xff0c;XMeter 团队全力聚焦于 …
阅读更多...
搭建Gerrit环境Ubuntu

搭建Gerrit环境Ubuntu

搭建Gerrit环境 1.安装apache sudo apt-get install apache2 注意:To run Gerrit behind an Apache server using mod_proxy, enable the necessary Apache2 modules: 执行:sudo a2enmod proxy_http 执行:sudo a2enmod ssl 使新的配置生效&#xff0c;需要执行如下命令:serv…
阅读更多...
ctfshow【菜狗杯】wp

ctfshow【菜狗杯】wp

文章目录webweb签到web2 c0me_t0_s1gn我的眼里只有$抽老婆一言既出驷马难追TapTapTapWebshell化零为整无一幸免无一幸免_FIXED传说之下&#xff08;雾&#xff09;算力超群算力升级easyPytHon_P遍地飘零茶歇区小舔田&#xff1f;LSB探姬Is_Not_Obfuscateweb web签到 <?ph…
阅读更多...
在社交媒体上行之有效的个人IP趋势

在社交媒体上行之有效的个人IP趋势

如果您认为无论是获得一份工作、建立一家企业还是推动个人职业发展&#xff0c;社交媒体都是帮助您实现目标的可靠工具&#xff0c;那么个人IP就是推动这一工具前进的燃料。个人IP反映了您是谁&#xff0c;您在所处领域的专业程度&#xff0c;以及您与他人的区别。社交媒体将有…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023