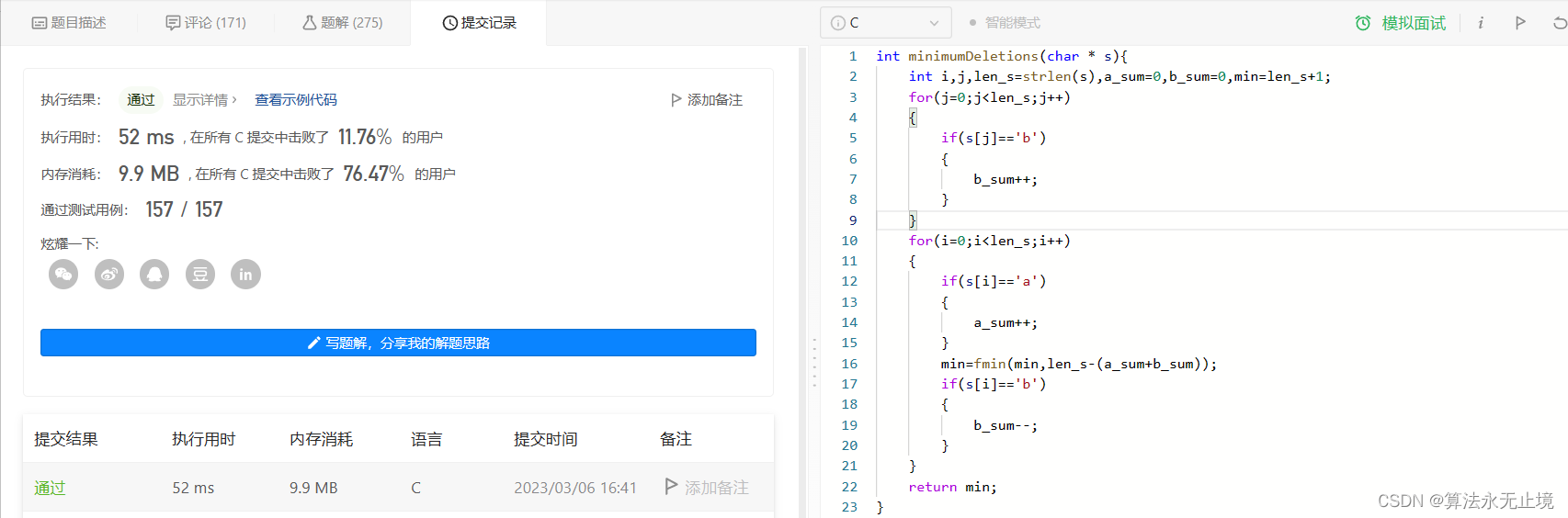
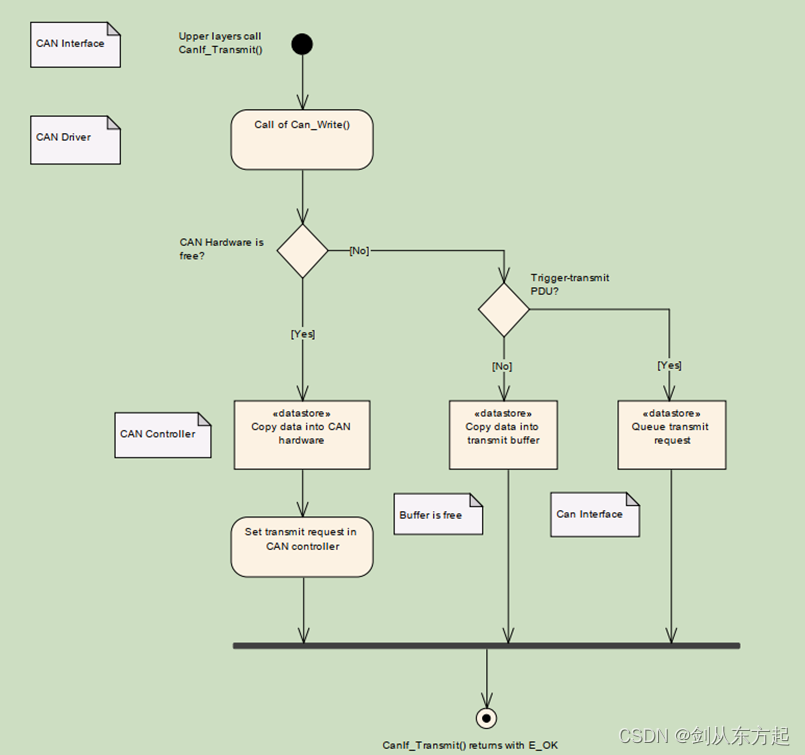
蓝桥杯真题31日冲刺 |第一天

一：完全平方数

题目：[链接](完全平方数 - 蓝桥云课 (lanqiao.cn))
思路：
- 将 每个完全平方数都消掉，剩下的就是不能构成平方的数
- 以12 为例：
- 所以 12 只要再乘个三即可满足

代码实现：

#include <iostream>
#include<cmath>
using namespace std;
int main()
{
  // 请在此输入您的代码
  long long  x;
  cin>>x;
  for(long long i=2;i*i<=x;i++)
  {
    while(x % (i*i) ==0) //将 每个 完全平方数都 消掉，剩下的就是 不能构成平方的数
    x /= i*i;
  }
  cout<<x<<endl;
  return 0;
}

总结：

所以，当我们遇到平方数求解的题时，我们要学会拆分！

这就是化繁为简，难题就是这样一步步变简单的！！

二：9数算式

题目：9数算式
思路：
1. 我们先看其中一种字符串的排列（化繁为简！！） --》
2. 所以只要我们列出所有排列中的所有 left,right 的取值，就能找到满足要求的 left,right

代码实现：

#include <iostream>
#include<algorithm>
using namespace std;

bool Is_Accord(int x)
{
  int v[10]={0};
  while(x!=0)
  {
    v[x%10] = 1;
    x = x/10;
  }

  for(int i=1;i<=9;i++)
  {
    if(v[i] !=1)
    return false;
  }

  return true;
}
int main()
{
  // 请在此输入您的代码
  //全排列 用 algorithm 里的 next_permutation 函数来获取 排列

  string s ="123456789";
  int count=0;
  do{
    //依次遍历，当前 序列下 --》 x,y的情况

    for(int i=1;i<=8;i++)
    {
      int  x = stoi(s.substr(0,i));
      int   y = stoi(s.substr(i));

      if(Is_Accord(x*y) == true)
      count++;
    }

  }while(next_permutation(s.begin(),s.end()));

  cout<<count/2;
  return 0;
}

总结：
1. next_permutation --> 获取该字符串的下一个全排列，包含在中
2. 依旧是化繁为简，先考虑其中一种情况，再推广到整体
3. 因为 left,right 是有对称重复的，所有算出来的值要 /2；

三：最少刷题数

题目：最少刷题数

思路：
1. 先创建一个排好序的数组 --》通过该数组找到第一个合格的刷题数
2. 按要求打印即可

代码实现：

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

int main() {
	// 请在此输入您的代码
	int n;
	cin >> n;

	vector<int> v(n, 0);
	for (int i = 0; i < n; i++)
		cin >> v[i];

	vector<int> tem = v;
	sort(tem.begin(), tem.end());

	int ans = 0;
	int i = 0;
	while (i < n) { //找到 第一个 合格 刷题数
		int j = i;
		//去除相等的个数
		while (j < n && tem[j] == tem[i]) {
			j += 1;
		}
		int right = n - j; //找到左边 小于于的 个数
		int left = i;

		if (left < right)
		{
			i = j;
			continue;
		}
		else if (left > right) { //找到了第一个 合格 刷题数
			ans = tem[i];
			break;
		}
		else {
			ans = tem[i] + 1;
			break;
		}
	}

	for (int k = 0; k < n; k++) {
		if (v[k] >= tem[i])
			cout << 0 << " ";
		else
			cout << ans - v[k] << " ";
	}

	return 0;
}

四：山

题目: 山

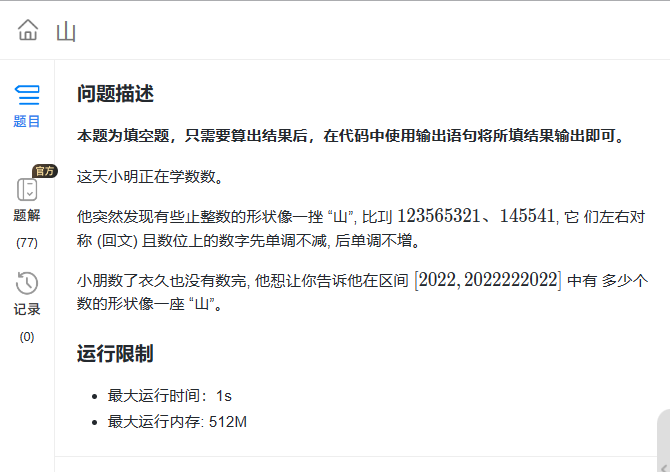
思路：
1. 一定不能暴力求解，会超时
2. 我们可以利用对称的思想：假如123是单调不减的，那么肯定有 123321 和 12321 这两个数满足题目要求
  - 所以我们可以分为几种情况：

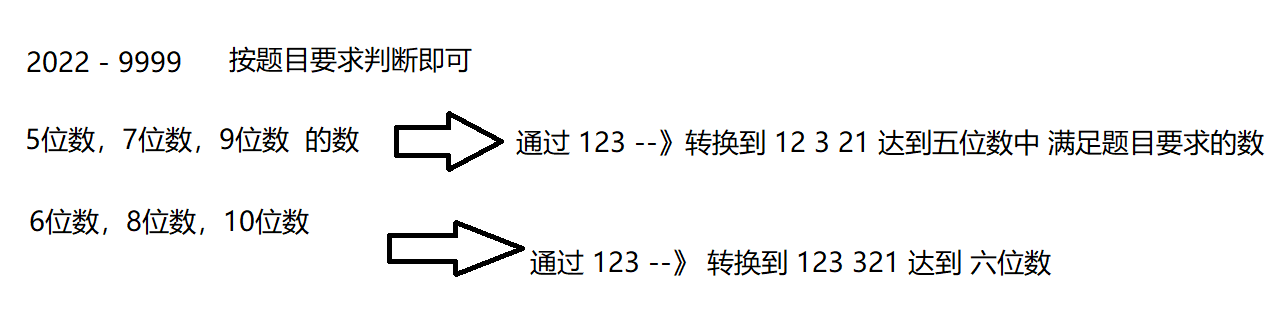
代码实现：

#include <iostream>
#include<sstream>
using namespace std;

int Is_Rccord(int x) //判断是否符合
{
  string s = to_string(x);
  int size = s.size();
  int mid = size/2;

  for(int i=0;i<mid;i++)
  {
    if(s[i] != s[size-1-i] || s[i] > s[i+1])
    return 0;
  }

  return 1;
}

int Is_Increasing(int x) //对称的 只要判断是否递增 就好了
{
    string s = to_string(x);

    for(int i=0;i<s.size()-1;i++)
    {
      if(s[i] > s[i+1])
      return 0;
    }

    return 1;
}

int main()
{
  // 请在此输入您的代码
  int ans=0;

  for(int i=2022;i<=9999;i++)
    ans += Is_Rccord(i);

  for(int i=100;i<=99999;i++) //奇数位 5 ，7，9
   ans +=Is_Increasing(i);

   for(int i=100;i<=20222;i++) //偶数位 6，8，10
   ans += Is_Increasing(i);

  cout<<ans;
  return 0;
}