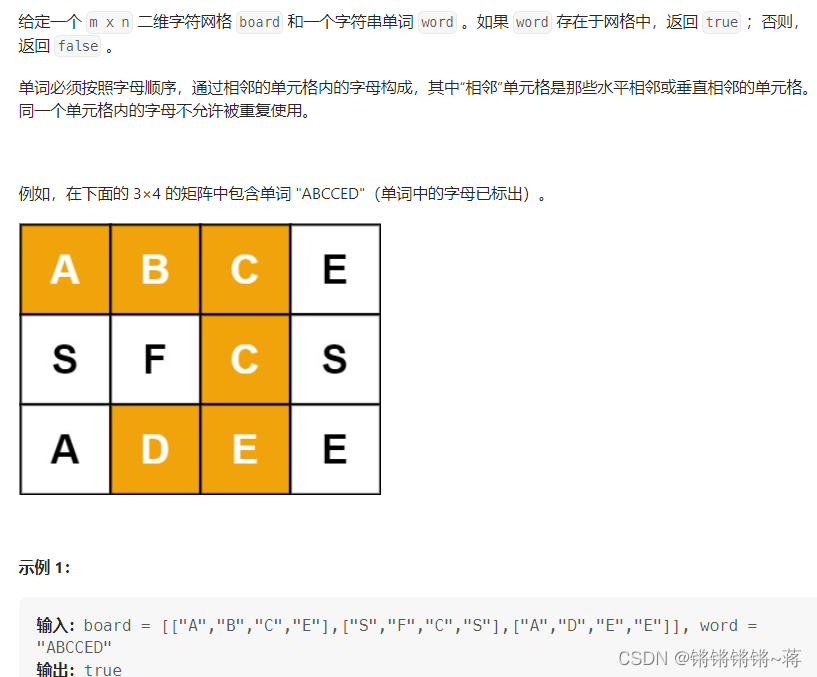
剑指 Offer 12. 矩阵中的路径

典型矩阵搜索题

DFS+剪枝

深度优先搜索： 可以理解为暴力法遍历矩阵中所有字符串可能性。DFS 通过递归，先朝一个方向搜到底，再回溯至上个节点，沿另一个方向搜索，以此类推。
剪枝： 在搜索中，遇到 这条路不可能和目标字符串匹配成功 的情况（例如：此矩阵元素和目标字符不同、此元素已被访问），则应立即返回，称之为 可行性剪枝 。

class Solution:
    def exist(self, board: List[List[str]], word: str) -> bool:
        def dfs(i,j,k):
            if not 0<=i<len(board) or not 0<=j<len(board[0]) or board[i][j]!=word[k]:
                return False
            if k==len(word)-1:
                return True
            board[i][j]=""
            res= dfs(i+1,j,k+1) or dfs(i-1,j,k+1) or dfs(i,j+1,k+1) or dfs(i,j-1,k+1)
            board[i][j]=word[k]
            return res
        for i in range(len(board)):
            for j in range(len(board[0])):
                if dfs(i,j,0):
                    return True
        return False

复杂度分析：
M,N分别为矩阵行列大小， K 为字符串 word 长度。

时间复杂度 O(3KMN) ： 最差情况下，需要遍历矩阵中长度为 KKK 字符串的所有方案，时间复杂度为 O(3^K)
；矩阵中共有 MN个起点，时间复杂度为 O(MN)。
方案数计算： 设字符串长度为 K ，搜索中每个字符有上、下、左、右四个方向可以选择，舍弃回头（上个字符）的方向，剩下 333 种选择，因此方案数的复杂度为 O(3^K)
空间复杂度 O(K) ： 搜索过程中的递归深度不超过 KKK ，因此系统因函数调用累计使用的栈空间占用 O(K)（因为函数返回后，系统调用的栈空间会释放）。最坏情况下 K=MN ，递归深度为 MN ，此时系统栈使用 O(MN)的额外空间。

作者：Krahets
来源：力扣（LeetCode）
好难写 ！！

面试题13. 机器人的运动范围

地上有一个m行n列的方格，从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动，它每次可以向左、右、上、下移动一格（不能移动到方格外），也不能进入行坐标和列坐标的数位之和大于k的格子。例如，当k为18时，机器人能够进入方格 [35, 37] ，因为3+5+3+7=18。但它不能进入方格 [35, 38]，因为3+5+3+8=19。请问该机器人能够到达多少个格子？

示例 1：
输入：m = 2, n = 3, k = 1
输出：3