2022年数维杯国际大学生数学建模挑战赛A题自动地震地平线跟踪解题全过程论文及程序

2022年数维杯国际大学生数学建模挑战赛

A题自动地震地平线跟踪

原题再现：

随着我国经济社会发展，地质工作的重要性也日益提高。地震资料解释是地震勘探工程的一个重要阶段，可以明确油气勘探的地下构造特征，为油气勘探提供良好和有利的储层;准确的地层信息是地震资料解读的基础，是储量预测的重要依据。地震地平层跟踪是地震资料解释的关键技术之一，良好的地震地平线跟踪方法可以大大提高地震资料解释的效率和准确性。
获取地下构造岩性和储层信息是地震勘探的主要目标，因为主地层界面一般是波阻抗界面较好的，地震波在地下介质中传播时受地层界面的影响，最终表现出不同的地震反射特征，如形态、地震反射均匀轴的强度、频率和连续性。地层界面的形状和埋藏深度等结构信息可以直接从地震数据中获得。由于这类结构信息是地震资料中最直观、最容易使用的信息，自地震勘探技术诞生以来，从地震资料中提取结构信息就成为地震勘探最重要的目标之一。
在反射地震资料中，地震波阻抗界面通常对应于地层界面或岩性界面，但岩性界面不能总是形成波阻抗界面，只有在那些波阻抗差足够大的相邻地层中才能形成波阻抗界面。虽然不同地质年代形成的地层岩性通常不同，但只有通过数百万年沉积压实和沉积间断层的交替，岩石物理性质的差异才能（密度、孔隙率等）在相邻地层之间揭示，岩性和岩石物理性质（差异）的组合将形成显著的波阻抗差异，因此，地震剖面上的地震反射事件轴通常对应于沉积等时表面而不是宏观岩性界面。根据这一理论，地震事件轴所指示的地层界面是地层沉积过程的不连续性，由于其相对等时性，这种沉积不连续性与地层的结构特征基本一致，因此，地震事件轴是识别地层界面的主要标志。地震事件轴的空间分布特征和时域变化特征是地平线解释的主要依据。地震事件轴也可用于获取地层倾角和方位角等信息。
在二维地震勘探时代和三维地震勘探初期，地震资料的地平线解释主要是单层，即从地震剖面中选择几个与强地层反射界面相对应的连续性好的地震事件轴进行跟踪。由于这种地平线解释方法效率低，在地震剖面上容易追踪的地震事件轴数量少，可以获得的地层数量有限，导致传统的地震结构解释模型无法获得详细的地质结构信息，因此对地质构造特征的详细描述不够清晰。也就是说，传统的地震地平线解说方法忽略或浪费了大量的地震信息，在精度和效率方面已经不能满足现代地震结构解说和地质综合研究的要求。随着三维地震勘探特别是高密度地震勘探技术的发展，获得的地震数据精度越来越高，地震数据数量不断增加，从地震数据中自动提取结构、岩性、流体等信息成为现代地震数据解释进展的关键，也是地球物理学家和地质学家正在努力的目标。
现有的地震地平线跟踪方法通常由地震地平线解释员手动完成。在地震数据的解释中，事件轴的跟踪非常重要。解释器主要基于地震波动力学和运动学特性，即振幅、同相或连续性、波形相似性三个标准和人工对比跟踪。人工地平线跟踪是利用波形相似度，人工跟踪二维地震剖面上底层的连续反射事件轴，得到地平线（地层界面），然后将所有地平线插值形成地平线面。然而，人工地平线跟踪对人工成本的需求量大，不仅耗时长，而且对地震勘探的效率影响很大。
为了克服跟踪时间效率低、结果可靠性差的问题，近年来研究人员开始高度重视自动水平跟踪方法。自动地平线跟踪方法是在地震迹线上搜索具有相似特征的“种子点”，搜索这些特征，满足条件后反复搜索下一个区域。该方法解决了地形较为复杂时人工地平线信息难以获取的问题，获得的信息比人工获取的信息更准确。
目前，有两种较好的自动水平跟踪标准，即基于波形特性的自动跟踪和基于相关性的自动跟踪。基于波形特征的自动跟踪是在搜索时间窗口中仅查找特征点的相似波形结构（波峰、波谷、过零点等），而地震迹线之间不进行相关性计算，逐个搜索定义的波谷、波峰和交叉点。由于地下局部区域之间的连续性和稳定性反映在地震时间剖面上，因此它是地震波反射层在相邻地震通道上地震波反射层幅值中的相似性和连续性。因此，基于相关水平自动跟踪算法，以种子点为中心，根据相关时间窗口范围，选择一个地震通道，将本段地震数据的地震数据与相邻通道搜索时间窗口中的地震数据相关联，如果在搜索时间窗口中找到符合条件的特征点，该点固定为新的种子点，然后选取下一个跟踪。

请根据所附数据建立数学模型，解决以下问题：

1.地震资料中经常有很多噪声，请使用有效的方法对附件数据进行降噪。

2.建立地震地层关联自动跟踪模型或设计相应的新跟踪算法，并对附件数据进行跟踪。

3.建立基于波形特征的自动跟踪模型或设计相应的新跟踪算法，并对附件数据进行跟踪。

4.评估两个自动跟踪模型（或算法）的结果，验证模型的合理性，分析实验获得的数据与实际数据之间的误差，并做出合理的解释。

5.建立基于相关性和波形的三维地平线自动跟踪模型，对附件给出的数据实施算法，实现地平线跟踪，对故障数据进行识别和分析。

整体求解过程概述(摘要)

在本文中，我们重点介绍了自动地震地层跟踪的算法。我们首先使用鲁棒的深度学习去噪算法对初始地震数据进行去噪，然后对去噪地震数据构建自动地震地层跟踪算法。我们主要利用深度学习中的全卷积网络U-net实现地震地层自动跟踪，通过在常见的地震DNA算法中引入聚类方法，提出了一种改进的地震DNA算法，以提高自动地层跟踪的连续性和准确性。最后，利用去噪地震资料建立基于相关性的波形三维级自动跟踪模型，并分析结果。

问题一：地震数据去噪。针对传统基于先验的建模方法无法准确描绘噪声分布，影响模型假设和参数设置的准确性，该文采用鲁棒深度学习去噪算法对原始地震数据进行去噪。首先将训练数据逐个放入深度学习网络模型中进行网络模型训练，然后保存训练好的模型参数，最后利用预训练参数进行测试，对比最佳测试结果，为原始地震数据的去噪过程选择最佳测试结果预训练参数。
问题二：基于全卷积神经网络的地震层自动跟踪算法。传统的层常规层跟踪技术主要在二维地震剖面上手动解释，解释员根据自己的经验和主观判断跟踪地震层。深度学习方法基于大量数据，通过构建合适的网络模型进行多级特征提取来预测数据。本文以U-net网络为基础，通过馈送大量数据对网络进行训练，使网络具有一定的地震层跟踪预测能力，通过有效提取地震数据中的特征，实现地震层自动跟踪的能力。
问题三：改进的地震DNA自动跟踪算法。传统的地震DNA算法在跟踪时需要扫描该区域的所有点，导致匹配更多符合条件的地震波，拾取地震层的连续性差。为此，我们通过在地震DNA算法中引入聚类方法来改进传统的地震DNA算法。通过对地震DNA算法发现的地震波进行分类，然后利用欧氏距离将聚类点连接起来，并利用相干算法对断裂区进行查找和屏蔽，使地震DNA算法发现的地震地层具有更好的连续性和准确性。
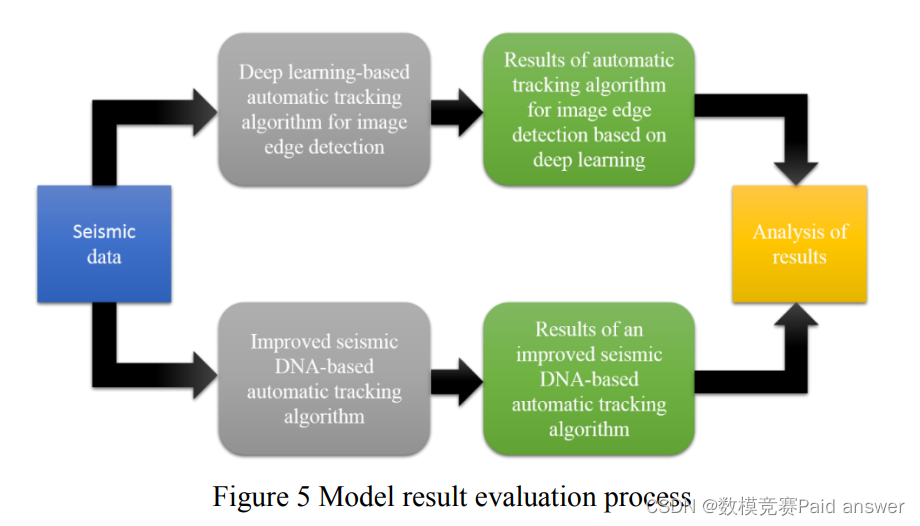
问题四：评估问题 2 和问题 3 中两种自动跟踪算法的结果。基于全卷积神经网络的地震层自动跟踪算法受噪声影响较大，主观性较强，部分边缘不够清晰，识别出的地震层杂乱无章。然而，改进的地震DNA自动跟踪算法可以同时拾取多个地震层，并且追踪的地震层更加连续，并且在断层位置没有级联发生。
问题五：基于相关性的波形三维水平自动跟踪模型。基于匹配搜索的全层跟踪方法主要基于时间方向上多层纵向分布的幅值特征和层间间隙特征，设计层纵向分布特征提取算法、基于匹配搜索的数据块生成算法和面向幅度的数据块连接算法。该方法采用层纵向分布的特征提取算法和基于匹配搜索的数据块生成算法，将三维地震图像中的极点连接成三维空间中的层块，采用基于幅值定向的数据块连接算法将层块连接起来，形成地震图像中的大层，然后通过扩展层的间隙问题得到最终的跟踪结果。

问题分析：

对问题一的分析

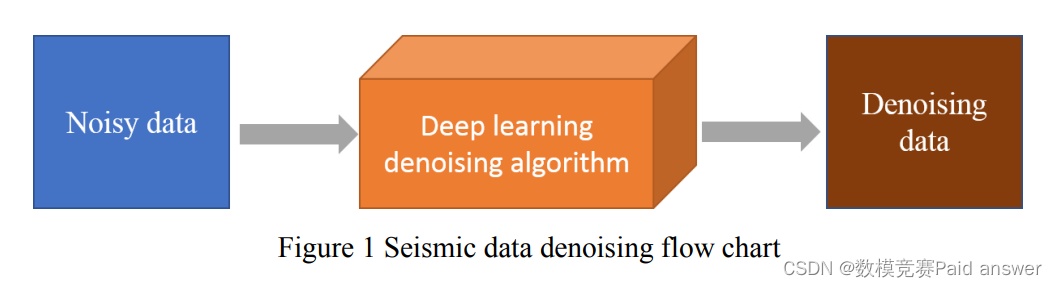
地震勘探数据中包含的噪声很复杂，传统的基于先验的建模方法无法准确描绘噪声分布。深度学习通过多层卷积神经网络自动提取数据的深层特征，并利用非线性逼近能力自适应学习复杂的去噪模型，为地震数据去噪带来了新思路。然而，目前基于深度学习的去噪方法在样本覆盖率不足时不具备较强的学习模型泛化能力，大大降低了去噪效果。为此，将使用一种强大的深度学习去噪算法来对初始地震数据进行降噪。具体的去噪过程如图1所示：
在这里插入图片描述

对问题二的分析

地层示踪是地震图像解释中非常重要的一部分，也是地震图像解释的一项基本任务。地震勘探是通过爆炸的方式激发地震波，由于不同地质构造中波阻抗的变化，声波在穿越不同地质构造时被岩层反射，反射波向上传输到地面被地面接收传感器接受和记录，这是最原始的地震记录。传统的层跟踪方法是在二维地震剖面上手动进行的，主要依靠解释员的主观判断，根据地震剖面中的波峰和波谷完成均质轴跟踪，在均质轴跟踪过程中，主要遵循三个标准：连续性、均匀性和波形相似性。
在这里插入图片描述
随着勘探力度的加大和勘探技术的成熟，地震资料越来越多，对勘探精度的要求也越来越高。这种费时费力的人工跟踪方法，容易受到译员主观性的影响，逐渐不能满足实际生产要求，因此自动地震水平跟踪算法的研究逐渐受到研究人员的重视。
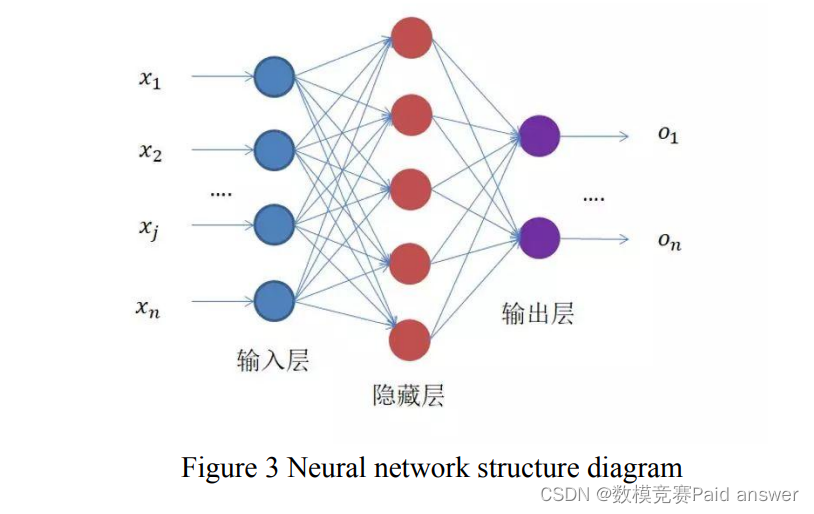
近年来，深度学习发展迅速，在不同领域得到广泛应用，越来越多的新算法应用于地震勘探数据的处理和解释，最具代表性的一种是神经网络方法。神经网络的结构如图所示。3、通过网络连接可以构建各种复杂的映射，实现数据特征的多级提取。
在这里插入图片描述

对问题三的分析

在地震数据的解释中，相轴的追踪非常重要。几十年来，口译员根据地震波的动力学和运动学进行了人工比较跟踪，即三个基本标准：振幅、同相或连续性和波形相似性。自1970年代以来，许多学者研究了地震波同相轴的自动跟踪和拾取方法，用不同的方法和不同的角度定量表达三个基本标准。人工地平线拾取是一种利用波形相似性手动描摹地层连续反射同相轴，然后将所有地平线插值形成地平线的方法。手动拾取具有效率低、精度差等缺点。为了克服跟踪时间效率低、结果可靠性差等问题，近年来研究人员越来越重视自动水平跟踪算法，自动水平跟踪的相关研究得到了迅速发展。
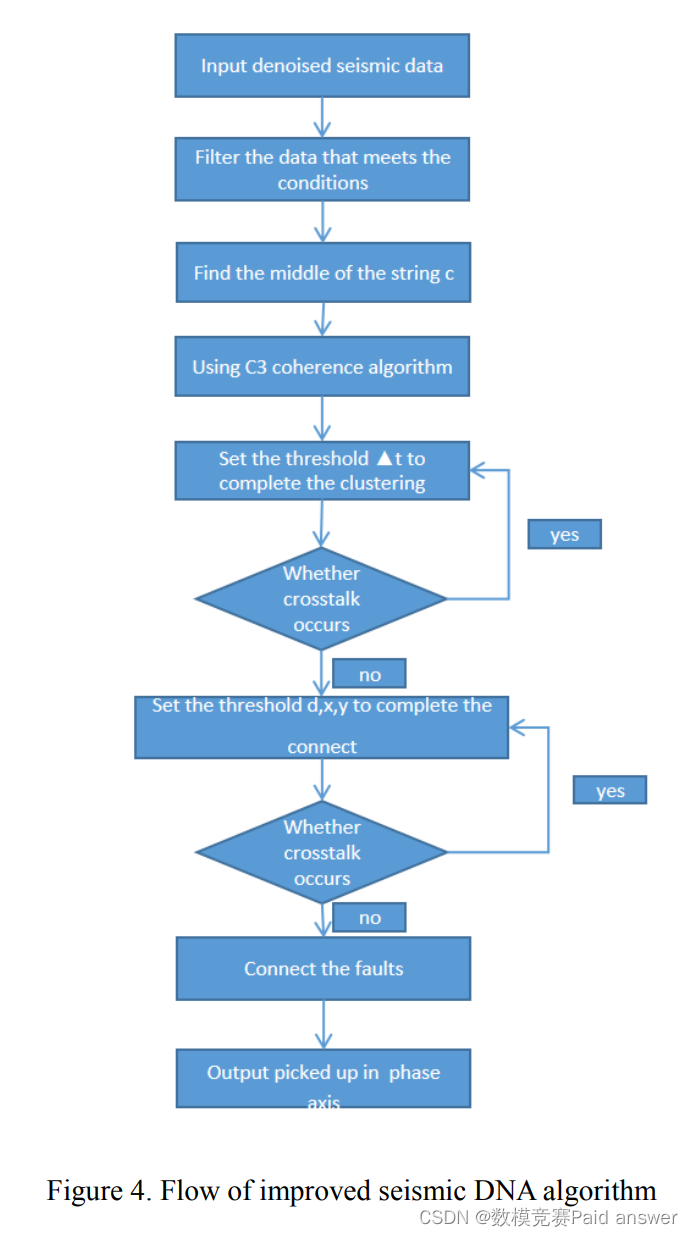
地震DNA算法是一种新型的地震级跟踪算法。其核心思想是通过某种转换将地震数据的数值信息转换为文本数据的字符信息，使地震数据可以作为文本数据进行搜索。该文基于地震DNA算法，提出了一种改进算法。在地震DNA算法中引入聚类方法，可以解决地震DNA算法匹配地震层连续性差、层划分不明显的问题。具体流程如图4所示：
在这里插入图片描述

对问题四的分析

从地震层信息、算法效率、模型合理性、数据误差和跟踪精度等方面分析了基于深度学习的图像边缘检测算法和问题2改进的地震DNA算法的结果。最后，评估两种算法的结果。模型结果评估的具体流程如图3所示：
在这里插入图片描述

对问题五的分析

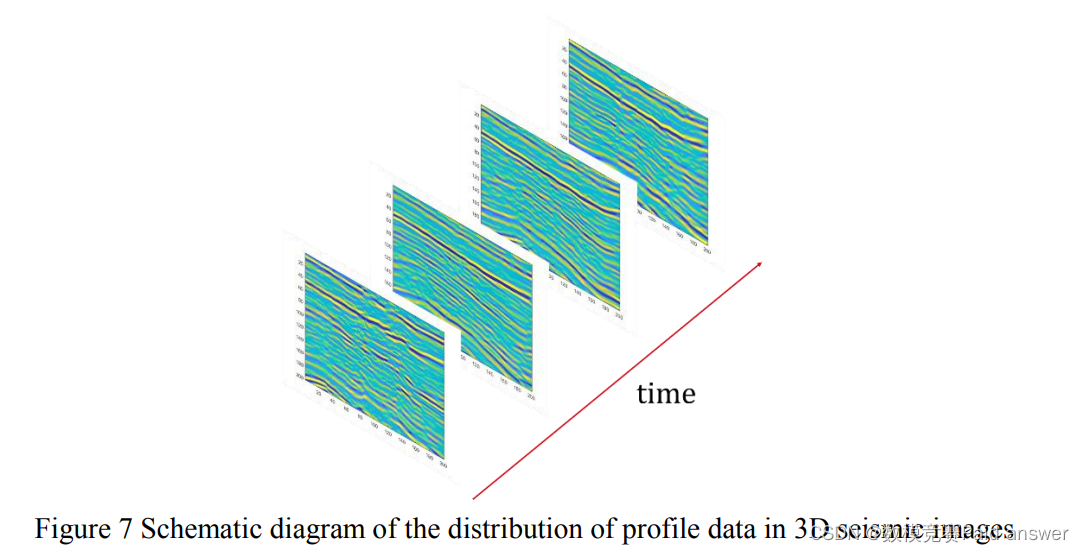
三维地震图像有三个方向，即内联方向、交叉线方向和时间方向。地震记录在3D地震图像中以沿时间方向分布的波形表示，3D地震图像在3D空间中的分布如图3所示，称为6D地震图像中的数据。三维地震数据是地震波形数据在内联中的分布，地震波形数据在内联和交叉剖面中的分布。这反映在波形幅度较小的3D地震图像中。
在这里插入图片描述
为了便于地震解释员的观察和使用，可以从三维地震数据体中提取剖面数据。剖面数据分为垂直剖面和水平剖面，沿垂直方向的剖面通常称为内联剖面;和垂直于主测量线的交叉线轮廓。剖面数据分布在3D地震图像中，如图3所示。不同的内联剖面或交叉线剖面在 7D 地震影像中水平分布，而内联剖面和交叉线剖面在 3D 地震影像中垂直正交。
在这里插入图片描述
随着高精度全数据采集系统的出现和发展，人工跟踪的工作量变得非常巨大，严重影响了地震解释的效率。生成 3D 全图层跟踪以解决手动解释的不足。本文提取了多个垂直相邻层的层纵向分布特征，并通过匹配和搜索层纵向分布特征，实现了三维地震图像中层的并行跟踪。

整体求解过程概述(摘要)

模型假设：

为了简化给定的问题并将其修改为更合适的模拟。实际上，我们做出以下基本假设。每个假设都有一个正当的理由。

假设数据集中单个缺失的数据不会对模型的建立和求解产生重大影响。

假设所选地震数据具有代表性且准确。

假设跟踪模型中所有影响因素的时间尺度相同。

假设实际情况与模型相同。

模型的建立与求解整体论文缩略图

在这里插入图片描述

全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可

程序代码：

import torch
import torch.nn as nn
import torch.nn.functional as F
class DoubleConv(nn.Module):
"""(convolution => [BN] => ReLU) * 2"""
def __init__(self, in_channels, out_channels, mid_channels=None):
super().__init__()
if not mid_channels:
mid_channels = out_channels
self.double_conv = nn.Sequential(
nn.Conv2d(in_channels, mid_channels, kernel_size=3, padding=1, bias=False),
nn.BatchNorm2d(mid_channels),
nn.ReLU(inplace=True),
nn.Conv2d(mid_channels, out_channels, kernel_size=3, padding=1, bias=False),
nn.BatchNorm2d(out_channels),
nn.ReLU(inplace=True)
)
def forward(self, x):
return self.double_conv(x)
class Down(nn.Module):
"""Downscaling with maxpool then double conv"""
def __init__(self, in_channels, out_channels):
super().__init__()
self.maxpool_conv = nn.Sequential(
nn.MaxPool2d(2),
DoubleConv(in_channels, out_channels)
)
def forward(self, x):
return self.maxpool_conv(x)
class Up(nn.Module):
"""Upscaling then double conv"""

def __init__(self, in_channels, out_channels, bilinear=True):
super().__init__()
# if bilinear, use the normal convolutions to reduce the number of channels
if bilinear:
self.up = nn.Upsample(scale_factor=2, mode='bilinear', align_corners=True)
self.conv = DoubleConv(in_channels, out_channels, in_channels // 2)
else:
self.up = nn.ConvTranspose2d(in_channels, in_channels // 2, kernel_size=2, stride=2)
self.conv = DoubleConv(in_channels, out_channels)
def forward(self, x1, x2):
x1 = self.up(x1)
# input is CHW
diffY = x2.size()[2] - x1.size()[2]
diffX = x2.size()[3] - x1.size()[3]
x1 = F.pad(x1, [diffX // 2, diffX - diffX // 2,
diffY // 2, diffY - diffY // 2])
x = torch.cat([x2, x1], dim=1)
return self.conv(x)
class OutConv(nn.Module):
def __init__(self, in_channels, out_channels):
super(OutConv, self).__init__()
self.conv = nn.Conv2d(in_channels, out_channels, kernel_size=1)
def forward(self, x):
return self.conv(x)
""" Full assembly of the parts to form the complete network """
from .unet_parts import *
class UNet(nn.Module):
def __init__(self, n_channels, n_classes, bilinear=False):
super(UNet, self).__init__()
self.n_channels = n_channels
self.n_classes = n_classes
self.bilinear = bilinear
self.inc = DoubleConv(n_channels, 64)
self.down1 = Down(64, 128)
self.down2 = Down(128, 256)
self.down3 = Down(256, 512)
factor = 2 if bilinear else 1
self.down4 = Down(512, 1024 // factor)
self.up1 = Up(1024, 512 // factor, bilinear)
self.up2 = Up(512, 256 // factor, bilinear)
self.up3 = Up(256, 128 // factor, bilinear)
self.up4 = Up(128, 64, bilinear)
self.outc = OutConv(64, n_classes)
def forward(self, x):
x1 = self.inc(x)
x2 = self.down1(x1)
x3 = self.down2(x2)
x4 = self.down3(x3)
x5 = self.down4(x4)
x = self.up1(x5, x4)
x = self.up2(x, x3)
x = self.up3(x, x2)
x = self.up4(x, x1)
logits = self.outc(x)
return logits
import torch
from torch import Tensor
def dice_coeff(input: Tensor, target: Tensor, reduce_batch_first: bool = False, epsilon=1e-6):
# Average of Dice coefficient for all batches, or for a single mask
assert input.size() == target.size()
if input.dim() == 2 and reduce_batch_first:
raise ValueError(f'Dice: asked to reduce batch but got tensor without batch dimension 
(shape {input.shape})')
if input.dim() == 2 or reduce_batch_first:
inter = torch.dot(input.reshape(-1), target.reshape(-1))
sets_sum = torch.sum(input) + torch.sum(target)
if sets_sum.item() == 0:
sets_sum = 2 * inter
return (2 * inter + epsilon) / (sets_sum + epsilon)
else:
# compute and average metric for each batch element
dice = 0
for i in range(input.shape[0]):
dice += dice_coeff(input[i, ...], target[i, ...])
return dice / input.shape[0]
def multiclass_dice_coeff(input: Tensor, target: Tensor, reduce_batch_first: bool = False, 
epsilon=1e-6):
# Average of Dice coefficient for all classes
assert input.size() == target.size()
dice = 0
for channel in range(input.shape[1]):
dice += dice_coeff(input[:, channel, ...], target[:, channel, ...], reduce_batch_first, epsilon)
return dice / input.shape[1]
def dice_loss(input: Tensor, target: Tensor, multiclass: bool = False):
# Dice loss (objective to minimize) between 0 and 1
assert input.size() == target.size()
fn = multiclass_dice_coeff if multiclass else dice_coeff
return 1 - fn(input, target, reduce_batch_first=True)
import matplotlib.pyplot as plt
def plot_img_and_mask(img, mask):
classes = mask.shape[0] if len(mask.shape) > 2 else 1
fig, ax = plt.subplots(1, classes + 1)
ax[0].set_title('Input image')
ax[0].imshow(img)
if classes > 1:
for i in range(classes):
ax[i + 1].set_title(f'Output mask (class {i + 1})')
ax[i + 1].imshow(mask[i, :, :])
else:
ax[1].set_title(f'Output mask')
ax[1].imshow(mask)
plt.xticks([]), plt.yticks([])
plt.show()