2022年第十二届MathorCup高校数学建模
B题 无人仓的搬运机器人调度问题
原题再现
本题考虑在无人仓内的仓库管理问题之一,搬运机器人 AGV 的调度问题。更多的背景介绍请参看附件-背景介绍。对于无人仓来说,仓库的地图模型可以简化为图的数据结构。
仓库地图:
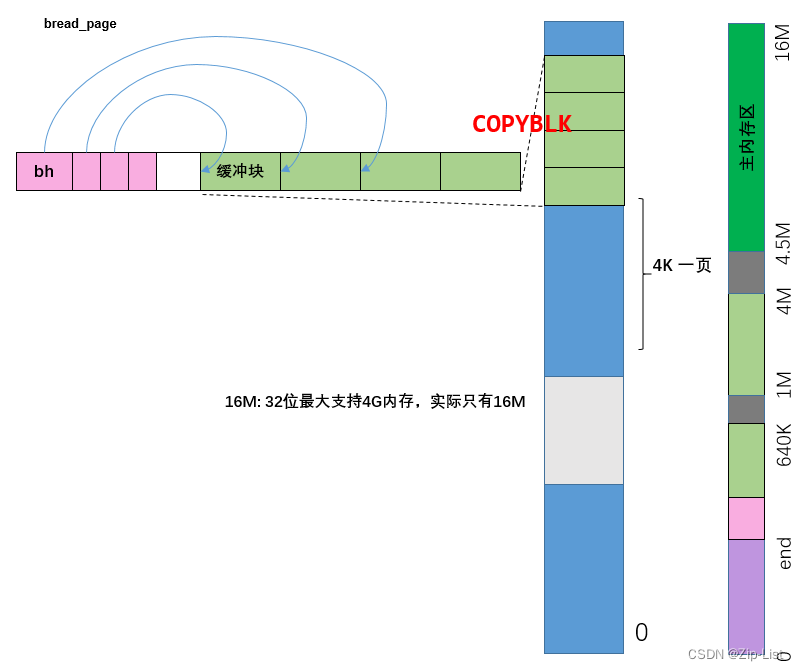
无人仓内的设施,可以细分为 AGV 能行驶的道路节点,和别的功能节点(如工位,储位等)。这样,仓库地图模型可以抽象为这些节点构成的图,再按 AGV 能到达的节点来添加图的边。简单来说,附件仓库地图数据(map.csv)通过描述节点类型,以及节点之间的关系(边),可以构建如下图 1 所示的仓库地图。
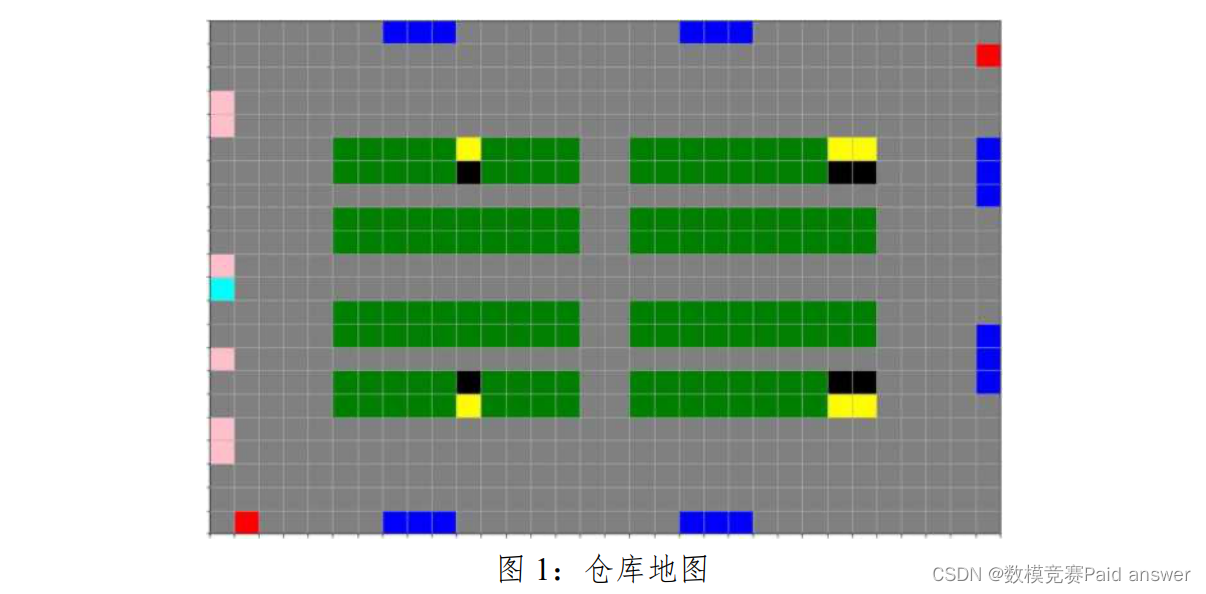
仓库地图数据(map.csv)是按 csv 格式存储,其节点类型有如下几类,在上图中用不同颜色标注。
1) 路径节点(灰色):AGV 可以自由通行。
2) 储位节点(绿色):放置托盘或者普通货架,AGV 可以到达。一般只有一个位置可以进出,即靠近道路的位置。
3) 保留节点(黄色):保留位置。
4) 柱子节点(黑色):障碍物,AGV 不能到达。
5) 拣选工位节点(蓝色):拣选机器人在这里把商品打包后从传送带出库,一般有多个托盘停靠位。
6) 补货位节点(粉色):从高密度区补货的商品放置点,一般通过传送带输送。
7) 空托盘回收节点(红色):空托盘回收处,图中只有两处。
无人仓任务场景:
假设仓库地图按上述方式抽象成图,搬运机器人 AGV—次只搬运一个托盘(带有多种商品),能执行从一个地图节点na移动到nb的路径指令,其中每一步只能移动到有边相连的地图节点,不能斜着移动。附件中机器人数据(agv.csv)里,给出了 20 个搬运机器人 AGV 在仓库地图上的初始位置坐标。
假设仓库内商品都是中大件商品,每个在储位的托盘上叠放着多种商品,附件中的库存数据(pallets.csv)给岀了全部托盘的位置以及托盘上放的商品信息。对于中件仓来说,即使用户订单包含了多个商品,实际发货还是一个商品一个包裹。这样,AGV 执行任务只需要尽快满足商品数目的要求,不需要等待同一订单中的全部商品到齐后才能出库。所以附件订单数据(orders.csv)里,每个订单只有同一件商品以及对应的数量。
无人仓流程是根据给定的一段时间内订单数据流,结合当前库存情况,统筹安排搬运机器人从储位搬运有需求商品的托盘到附近的拣选工位(即出库任务),拣选完成后需安排搬运工位处的非空托盘到空储位(即回库任务),或者安排搬运工位处的空托盘到托盘回收处(即回收任务)等。本题只考虑这三种主要任务场景,即出库、回库、回收任务。
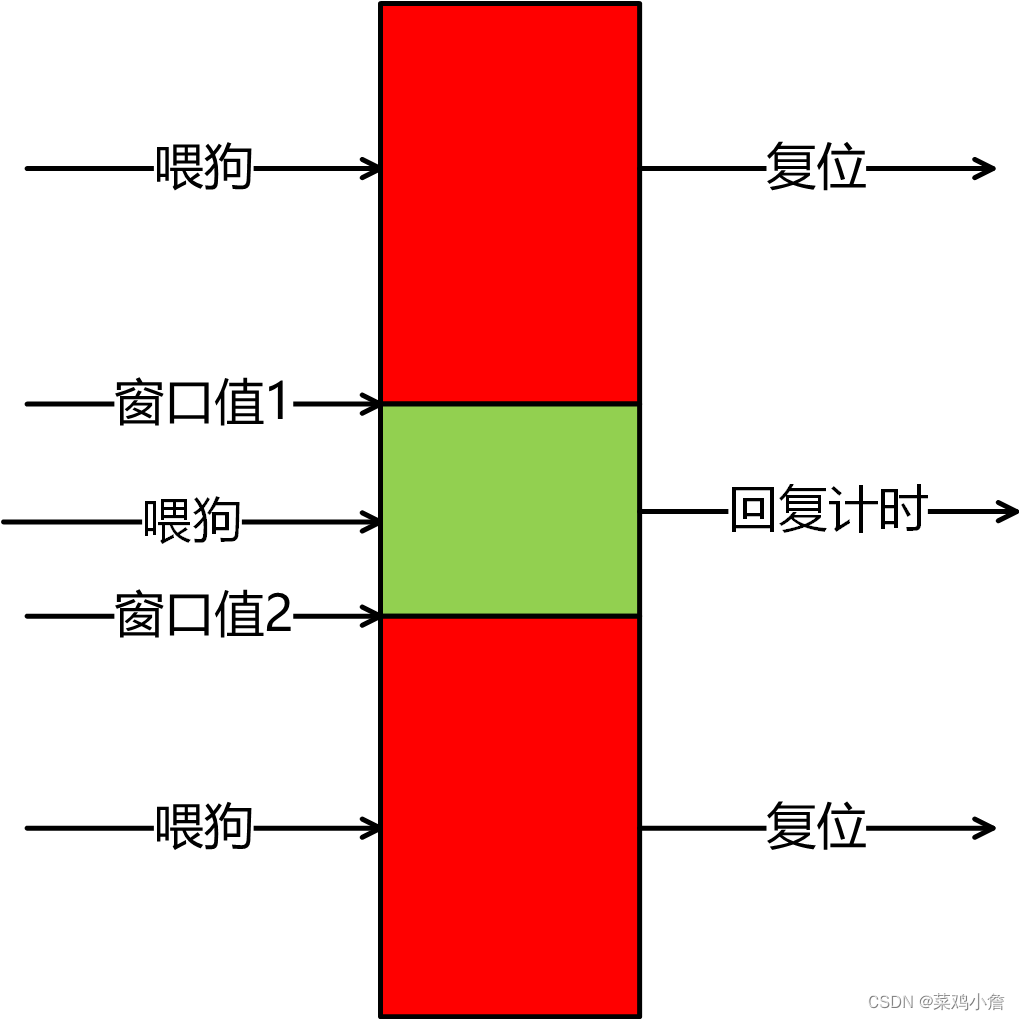
首先,对于出库任务,搬运机器人 AGV 把一个托盘搬运到拣选工位。但是对于同一个工位来说,同时能容纳放置的托盘数目是有限的。假设每个拣选工位有 b 个停靠位,也就是能同时最多分派 b 个出库任务到同一个拣选工位,直到执行回库或者回收任务,有空停靠位后才能容纳新的出库托盘。
其次,出库任务完成后,搬运机器人处于空闲状态,可以被安排执行下一个任务,而不需要在停靠位等候着。不妨假设出库托盘在拣选工位需要停留一段时间后,等拣选机器人打包发货后才能进行后续的回库或者回收任务。这里假设停留时间固定为t0,也就是说,无论需要拣选多少商品,都简化为停留时间t0后,该托盘可以被执行后续的回库和回收任务。
无人仓总结:
无人仓的主要运行场景就是安排搬运机器人 AGV 执行如下各种任务。
•出库:AGV 搬运载有商品的托盘到空闲拣选工位
•回库:AGV 搬运拣选完成的托盘从工位回到仓库内空储位
•回收:AGV 搬运拣选完成的空托盘从工位到托盘回收处
无人仓的核心是统筹优化上述任务的执行来最大化出库效率,安排AGV 任务和路线需满足全局最优,达到实时响应,并避免拥堵/死锁等情况发生。也需要均衡拣选工位之间的工作量。
问题 1:AGV 统筹调度的最佳策略
假设先不考虑搬运机器人在执行任务时可能的碰撞问题,请在无人仓模型下设计调度算法,根据附件中订单数据(orders.csv),和仓库内的库存数据(pallets.csv),对于给定的 20 个搬运机器人(agv.csv),统筹调度和安排 AGV 任务,直到满足所有的订单需求,即全部拣选工位都空闲为止。这里,目标函数为在每个搬运机器人尽可能忙的同时,最小化全部搬运机器人的行走总路径。
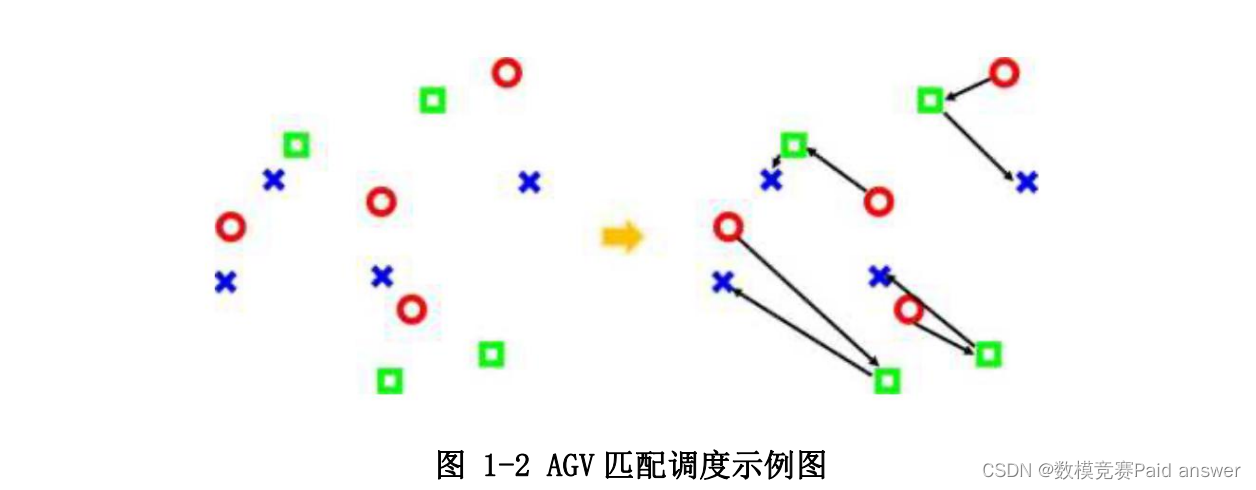
下面左图中,用红色圆圈表示 AGV,用绿色方块表示货架或者托盘,用蓝色 X 表示拣选工位。右图中匹配了最近的 AGV、托盘和工位,使得指定AGV 去取托盘后再送到工位拣选。
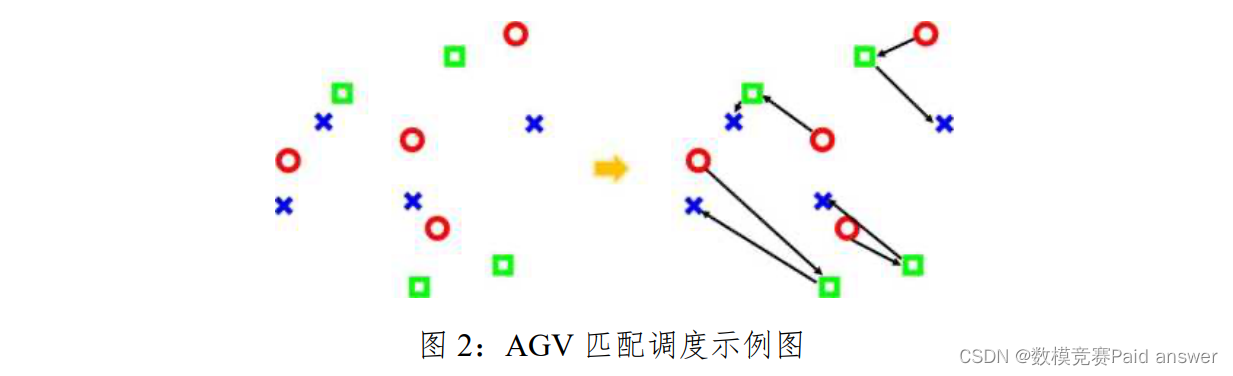
注意,现实场景中的目标其实是全局优化出库效率,节省人力,避免高峰期出现"爆仓”现象。所以更合适的衡量指标是时间上的,要求在最短的时间内满足订单需求。在某种程度上,目标可以转化为使得每个拣选工位尽可能忙,即最小化最忙拣选工位的工作时长。另一方面,仓库内搬运机器人 AGV 的合理投放数量一般是拣选工位的常数倍,因为投放太多的话出库效率不但不会改善,反而增加 AGV 拥堵的可能性。进一步考虑到每个工位可以增加停靠位,而且搬运机器人除了出库任务,还有回库和回收等任务。所以使得每个 AGV 尽可能忙,然后最小化全部 AGV 行走总路径,也是合理的模型目标简化。
问题 2:任务均衡区域划分
为了更好地平衡拣选工位的负载,同时预防搬运机器人的局部拥堵,根据拣选工位和库存商品数量对仓库地图进行动态分区。也就是对仓库内储位上的每个托盘,都指定一个默认拣选工位。
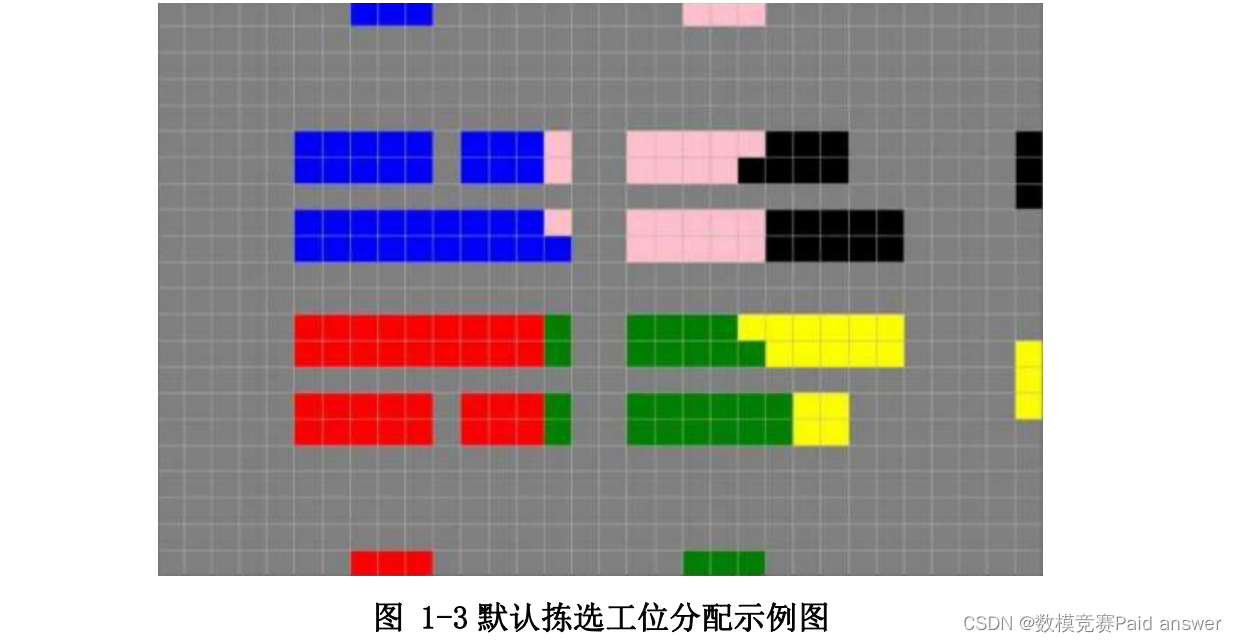
请建立优化模型,使得每个拣选工位对应托盘的商品总量尽可能地平均,同时要求最小化全部托盘到其默认拣选工位距离总和。类似下图 3 所示的区域划分。
进一步,根据某段时间内所需出库商品的库存分布,再结合问题一的AGV 调度算法,更合理地均衡每个拣选工位在某段时间内的工作量。
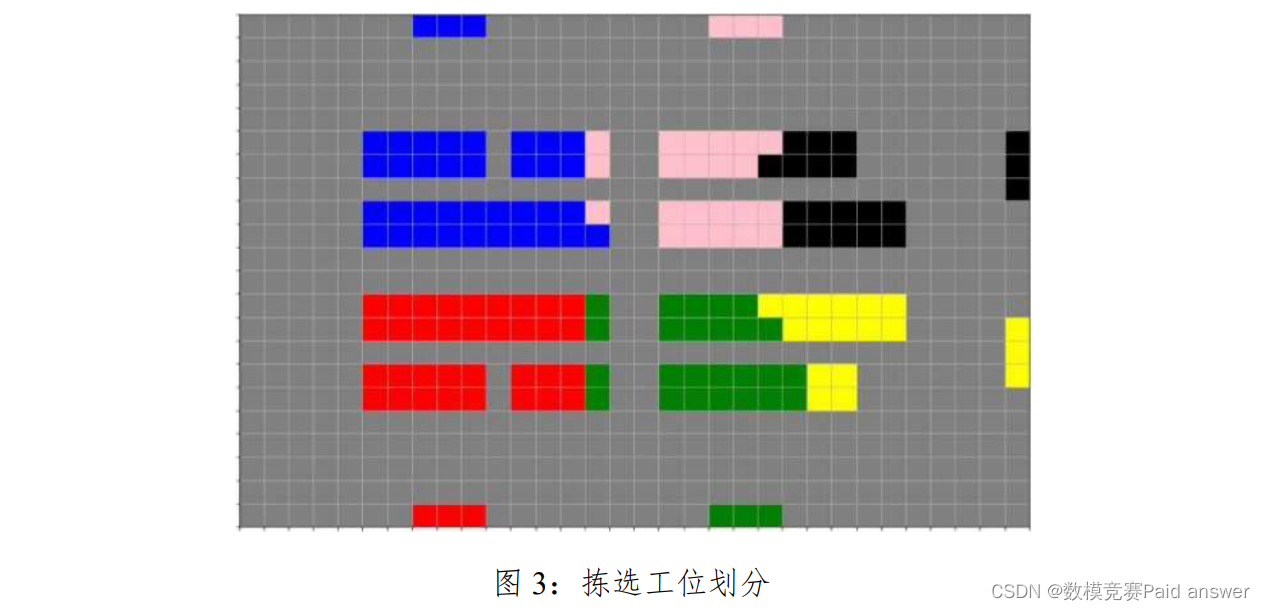
问题 3:避免碰撞和拥堵
在问题一和问题二的基础上,进一步考虑搬运机器人的碰撞和拥堵问题。当仓库内同时有多个 AGV 在执行任务时,不可避免有些 AGV 在某个路径节点上相遇。特别地,如果两个 AGV 在一条货架窄巷道上相遇,那么需要其中一个 AGV 避让。
在合理的假设下,请设计算法和防碰撞策略,使得搬运机器人能智能地避免碰撞。特别是在一些特殊节点处(如托盘回收处),避免出现多个AGV 的拥堵,和可能的死锁场景。
下图是一个死锁场景示例,一个 AGV 去拣选工位取空托盘,另一台AGV 去相邻停靠位放置托盘,他们占据了各自的前进路径节点后都不退让,造成了死锁。
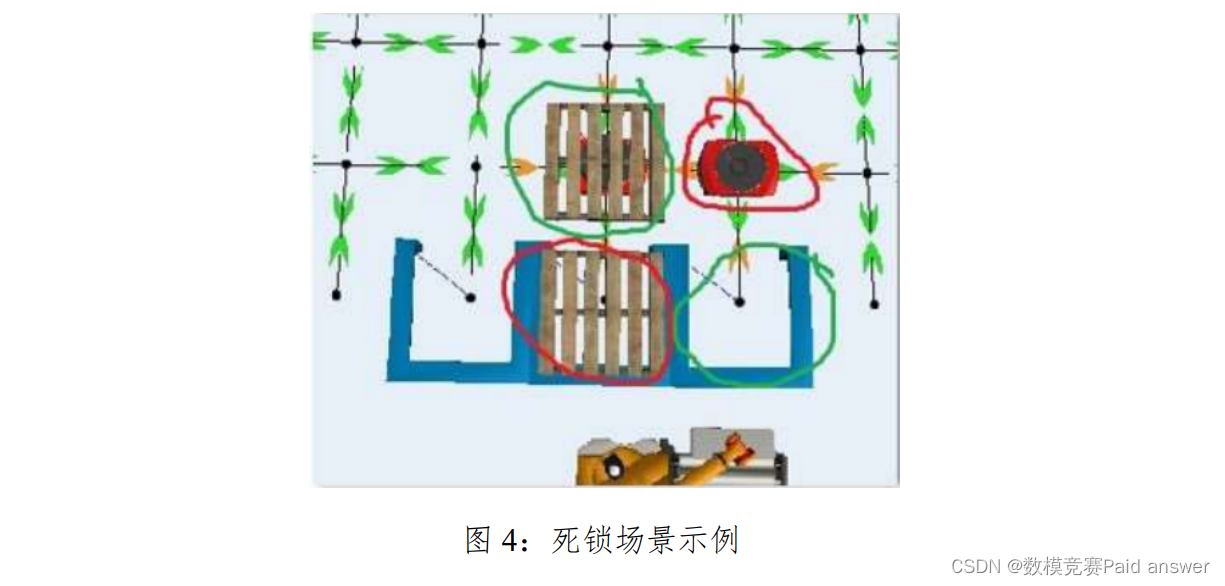
整体求解过程概述(摘要)
针对无人仓的多搬运机器人的路径规划问题,本文综合运用了多目标规划、遗传算法和交通管制法等方法,充分发挥了线性加权和 banach 空间中的向量范数等思想的优势,根据题意构建具体的线性规划模型,并借助 python 软件编程求解。
首先我们对给出的数据进行数据预处理:1)根据 map.csv 中的仓库地图数据,基于每一个节点的坐标画出无向图,基于节点关系构建出邻接矩阵;2)根据邻接矩阵,运用 Floyd 算法求解每个点到其他点的最短距离,得到距离矩阵和路由矩阵;3)通过Python 软件以栅格的形式进行可视化呈现。通过可视化的栅格仓库图,删除不符合实际的数据,因此,在该无人仓中实际可用的小车数量为 19 辆。
针对问题一,本题要求满足以下约束:1)满足所有的订单需求,即实现全部拣选工位都空闲;2)保证在搬运过程中每个机器人尽可能忙;3)每个拣选工位同时容纳的托盘数不超过 3 个停靠位,最终实现最小化全部搬运机器人的行走路径的目标函数。因此,根据题意,我们构建单目标规划模型,基于托盘搬运顺序进行编码,并采用改进的遗传算法和模拟退火两种方法进行对比求解。通过改进的遗传算法求解后可以得到,所有 AGV 的路径总长度为 7316;通过模拟退火算法求解后可以得到所有 AGV 的路径总长度为 7428。通过两种方式的比较,可以得到改进遗传算法使得 AGV 以更短的路径搬运完所需要的商品。
针对问题二,本题需要满足以下约束:1)每个拣选工位对应托盘的商品总量尽可能地平均;2)最小化全部托盘到其默认拣选工位距离总和;3)对仓库内储位上的每个托盘,都指定一个由第一阶段的目标规划唯一确定的默认拣选工位,最终实现全部搬运机器人的行为总路径最小的目标函数。本题在问题一的基础上,需要对仓库进行合理分区。因此,本题建立了两阶段的目标规划模型,其中约束条件 1)和 2)属于第一阶段动态分区规划模型,目的是为了实现仓库的合理分区,约束条件 3)则是在第一阶段的基础上新增加的约束条件,属于第二阶段的路径规划模型。本题设计一种具有新型编码方式的遗传算法来实现储位的分区,通过求解后可以得到在分区情况下所有 AGV 的移动总路径长度为 7453。
针对问题三,本题在满足问题一和问题二的基础上,需要进一步考虑搬运机器人的碰撞和拥堵问题。首先本文确定了路径冲突的三种类型:垂直冲突、相向冲突和追尾冲突,以及通过向量内积进行路径冲突类型的判断。其次,我们建立了交通管制法和优先级规划法模型,并在 AGV 为 12-19 辆的不同情况下均进行 100 次随机实验,最终得到最优的 AGV 数量规划,防止多 AGV 在仓库内的碰撞和拥堵问题。通过模型的求解可以得到在交通管制法下所有 AGV 的总路径最短,且当 AGV 数量减少为 15 时,减少碰撞和拥堵情况是最佳的。
模型假设:
1. 搬运机器人 AGV 完成出库任务后不在停靠位等候,立刻进行回库或者回收任务(且下一个托盘到达拣选工位节点时,前一个托盘必定已完成拣选工作),若拣选工位无托盘,则直接进行下一次出库任务。
2. 满足所有的订单需求时,托盘可置于拣选工位,搬运机器人 AGV 不需要进行回库或者回收任务。
3. 保留节点,视为柱子节点,即障碍物,搬运机器人 AGV 不能到达。
4. 若订单中的货物量超过储位的总量,由补货位节点从高密度区补货的商品放置点通过传送带进行输送,此时不增加搬运机器人 AGV 的工作负担。
5. 出库托盘在拣选工位需要停留一段时间后,等拣选机器人打包发货后才能进行后续的回库或者回收任务。
6. 搬运机器人 AGV 在工作时进行匀速运动,且各相邻栅格间的距离相等,搬运机器人 AGV 通过一个栅格均需要一个单位时间。
7. 假设搬运机器人 AGV 不再进行新任务,但全部拣选工位未都空闲为止时,将搬运机器人 AGV 从拣选工位节点人工移出。
问题分析:
问题一的解析
问题一在不考虑 AGV 机器人存在可能碰撞的问题,设计多 AGV 的调度算法,需要满足以下目标:(1)满足所有订单;(2)让每个机器人尽量忙;(3)全部搬运机器人的行走总路径最小;(4)最忙拣选工位的工作时长最短;(5)在最短的时间内满足订单需求。通过本题的求解,我们可以得到一个合理的多 AGC 的路径规划。具体如图 1-2,红色圆圈表示 AGV,绿色方块表示货架或者托盘,蓝色 X 表示拣选工位,左图为初始各点的分布状态,右图为匹配了最近的 AGV、托盘和工位,使得指定 AGV 去取托盘后再送到工位拣选。
问题二的解析
为了更好地平衡拣选工位的负载,同时预防搬运机器人的局部拥堵,根据拣选工位和库存商品数量对仓库地图进行动态分区。也就是对仓库内储位上的每个托盘,都指定一个默认拣选工位。本题要在问题一的基础上,对 AGV 调度算法进行优化,使得每个拣选工位对应托盘的商品总量尽可能平均,同时要求最小化全部托盘到其默认拣选工位距离总和,更加合理地均衡每个拣选工位在某段时间内的工作量。如图 1-3,对储位区域进行分区,为其分配相对应的默认拣选工位。
问题三的解析
本题考虑了 AGV 的碰撞和拥堵问题,当仓库内同时有多个 AGV 在执行任务时,不可避免有些 AGV 在某个路径节点上相遇,甚至在一些特殊节点处(如托盘回收处),可能还会出现多个 AGV 的拥堵甚至死锁场景。在这样的情况旨在,势必需要有 AGV进行避让,因此本题在问题一和问题二的基础上,考虑可能出现的碰撞情形,在合理的假设下,优化算法,使其具有一定的防碰撞能力。
模型的建立与求解整体论文缩略图


全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:(代码和文档not free)
The actual procedure is shown in the screenshot
#include<bits/stdc++.h>
#define MAXN 60 //最大工作量
#define INIT_PRE 3000//道路初始信息素量
#define K 2000 //循环次数
#define DIS 0.5 //信息素消散速率
#define SUPER_START 48
using namespace std;
int totalStep;
int Step[MAXN];
int phe[MAXN][MAXN][MAXN][MAXN];
int n,m;
struct Pair
{
int i,j;
void get(int a,int b)
{
i=a;j=b;
}
}Jobnum[MAXN];
struct Job
{
int machine;
int len;
}job[MAXN][MAXN];
struct Ant
{
int JobStep[MAXN]; //任务已运行步数
int path[MAXN];
int pathlen;
int getFullPath()
{
int sum=0;
for (int i=0;i<pathlen;i++)
sum+=path[i];
return sum;
}
Pair paths[MAXN];
};
void init()
{
//totalStep=0;
memset(phe,0,sizeof(phe));
for (int i=0;i<totalStep;i++)
for (int j=0;j<totalStep;j++)
for (int k=0;k<totalStep;k++)
for (int l=0;l<totalStep;l++)
phe[i][j][k][l]=INIT_PRE;
for (int i=0;i<totalStep;i++)
for (int j=0;j<totalStep;j++)
phe[SUPER_START][SUPER_START][i][j]=INIT_PRE;
return;
}
void Dissipation()
{
for (int i=0;i<totalStep;i++)
for (int j=0;j<totalStep;j++)
for (int k=0;k<totalStep;k++)
for (int l=0;l<totalStep;l++)
phe[i][j][k][l] *= DIS;
for (int i=0;i<totalStep;i++)
for (int j=0;j<totalStep;j++)
phe[SUPER_START][SUPER_START][i][j]*= DIS;
return;
}
struct Recording
{
int start;
int ed;
int job;
int machine;
};
int timeCalcu(int Job[], bool draw)
{
int sum=0;
int machineWorkTime[MAXN];
int JobLast[MAXN];
int JobStep[MAXN];
Recording rec[MAXN];
memset(machineWorkTime,0,sizeof(machineWorkTime));
memset(JobLast,0,sizeof(JobLast));
memset(JobStep,0,sizeof(JobStep));
memset(rec,0,sizeof(rec));
for (int k = 0; k < totalStep; k++)
{
int i = Job[k];
rec[k].start = max(JobLast[i],machineWorkTime[job[i][JobStep[i]].machine]);
rec[k].job = i;
rec[k].ed = rec[k].start + job[i][JobStep[i]].len;
JobLast[i] = rec[k].ed;
rec[k].machine = job[i][JobStep[i]].machine;
machineWorkTime[job[i][JobStep[i]].machine] = rec[k].ed;
JobStep[i]++;
}
for (int i = 0; i < m; i++)
{
sum = max(sum,machineWorkTime[i]);
}
if (draw == true)
{
int gantt[MAXN][MAXN];
memset(gantt,0,sizeof(gantt));
for (int i=0;i<totalStep;i++)
{
for (int j=rec[i].start;j<rec[i].ed;j++)
{
gantt[rec[i].machine][j]=rec[i].job+1;
}
}
for (int i=0;i<m;i++)
for (int j=0;j<sum;j++)
printf("%d%c",gantt[i][j],j==sum-1?'\n':' ');
}
return sum;
}
int main()
{
while (~scanf("%d%d",&n,&m))
{
totalStep = 0;
for (int i=0;i<n;i++)
{
scanf("%d",&Step[i]);
totalStep+=Step[i];
for (int j=0;j<Step[i];j++)
{
scanf("%d%d",&job[i][j].machine,&job[i][j].len);
}
}
init();
int antnum=totalStep*2;
Ant ant[antnum+5];
Ant bestAnt;
int bstime = 999999;
for (int sl=0;sl<10;sl++)
{
//printf("%d/10\n",sl);
srand(time(0));
memset(ant,0,sizeof(ant));
for (int i=0;i<antnum;i++)//第i只蚂蚁的旅程
{
//printf("sl=%d/%d\n",i,antnum);
int nowJob=SUPER_START; //作为图的超级源点
ant[i].JobStep[nowJob]=SUPER_START;
for (int j=0;j<totalStep;j++)
{
int allpre=0;
for (int k=0;k<m;k++)
{
//printf("i:%d j:%d k:%d l:%d ant:%d\n",nowJob,ant[i].JobStep[nowJob],k,ant[i].JobStep[k],i);
if (ant[i].JobStep[k]==Step[k]) continue;
allpre += phe[nowJob][ ant[i].JobStep[nowJob] ][k][ ant[i].JobStep[k] ];
}
//printf("%d\n",allpre);
int randSelectNum = rand()*rand() % allpre;//printf("OK\n");
//printf("摇到的数字是:%d\n",randSelectNum);
int select=0;
while (randSelectNum>=0)
{
if (ant[i].JobStep[select]==Step[select]) {select++;continue;}
randSelectNum -= phe[nowJob][ ant[i].JobStep[nowJob] ][select][ ant[i].JobStep[select] ];
select++;
}
select--;
//printf("蚂蚁选择了%d\n",select);
//蚂蚁选中的任务
ant[i].path[ant[i].pathlen]=select;
ant[i].paths[ant[i].pathlen++].get(select,ant[i].JobStep[select]);
ant[i].JobStep[select]++;
nowJob = select;
//printf("选择任务%d 阶段%d\n",select,ant[i].JobStep[select]);
}
}
Dissipation(); //每次蚂蚁行走完后,信息素都会消散
for (int i = 0; i < antnum; i++)
{
int ans = timeCalcu(ant[i].path,false);
if (ans<bstime && totalStep<=ans)
{
bstime = ans;
bestAnt = ant[i];
}
int reward = 2000/ans; //答案越小,奖励越多。
for (int j=0;j<ant[i].pathlen-1;j++)
{
int a = ant[i].paths[j].i;
int b = ant[i].paths[j].j;
int c = ant[i].paths[j+1].i;
int d = ant[i].paths[j+1].j;
phe[a][b][c][d] += reward;
}
}
//if (sl==1999)
/*for (int i = 0; i < antnum; i++)
{
for (int j=0; j<ant[i].pathlen; j++)
{
printf("%d%c",ant[i].path[j]+1,j==ant[i].pathlen-1?'\n':' ');
}
printf("\n%d\n",timeCalcu(ant[i].path,true));
}*/
}
printf("bestTime:%d\n",bstime);
printf("甘特图:\n");
timeCalcu(bestAnt.path,true);
printf("加工顺序为:");
for (int i=0;i<totalStep;i++)
printf("%d%s",bestAnt.path[i]+1,i==totalStep-1?"\n":"->");
/*int a[10] = {1,2,1,0,2,1,0,0};
timeCalcu(a,true);*/
return 0;
}
}